船撞海上风电单桩基础结构剩余强度研究

元国凯，方辉，马兆荣，孙计勃，汤东升

（1.中国能源建设集团广东省电力设计研究院有限公司，广州 510663；2.中国海洋大学 工程学院，山东 青岛 266100）

0 引言

海上风电是目前海上绿色能源开发和利用的最主要形式之一。在风电装备服役中，已多次出现船舶失控撞击风电基础结构事件，导致风电基础结构损伤，承载性能发生改变，造成严重安全隐患及巨大损失[1]。2017-08-20T14：00，台风“天鸽”在西北太平洋洋面生成，之后强度不断加强。2017-08-23，“天鸽”直面经过珠海金湾海上风电场项目海域，导致周边大型船舶进入风电场，造成风电基础结构严重受损。由于缺少计算方法和相应规范，无法实施损伤结构的承载性能评估，只得对该风电基础结构进行拆除。这次事故对后续工程的设计、施工、维护产生了巨大影响，直接导致保险费用飙升，因此需要对风电基础结构船撞损伤及其受损后结构剩余强度计算方法进行研究。

风电单桩属于大直径薄壁渐变钢管筒桩结构，桩基打入土体深53～57 m，本文选取55 m作为研究对象。针对含桩-土作用的单桩基础风电整体极限强度问题，采用现场试验或比例模型试验成本较高，多采用有限元法数值求解分析。栗铭鑫[2]针对直径为2 m的短桩结构进行复合加载下数值求解极限承载力分析，得出其水平荷载-水平位移承载性能曲线。俞益铭[3]总结了大直径桩基水平承载力的研究方法和桩体破坏模式。郝二通[4]利用有限元软件LS-DYNA进行船舶与单桩基础碰撞研究，对能量转化、最大碰撞力、基础损伤状态和风机动力响应等问题进行了探讨。Bela[5]和LeSourne[6]等将船艏简化为解析刚体，从能量（内能）变化、碰撞力-凹陷位移的角度评估碰撞的变化。

目前，海工结构剩余强度研究主要针对已知损伤位置和损伤程度的海洋平台或船体结构。邹湘[7]采用疲劳断裂力学的裂纹扩展方法，通过引入多尺度有限元原理，建立了时变裂纹损伤下的导管架平台数值计算模型，针对导管架的损伤较大区域进行了结构剩余强度研究。李景阳[8]综合考察了在复杂载荷作用下船舶结构产生的裂纹缺陷，提出了带裂纹构件的剩余极限强度评估方法。黄震球[9]等研究了船体梁结构由于内部爆炸导致结构受损后剩余强度的变化规律。

船舶碰撞过程涉及结构质量分布特征和材料非线性以及船艏碰撞接触非线性问题，需采用船舶-风电结构-土体全尺寸耦合模型与动态显式计算方法进行分析；船撞后结构剩余强度研究要求在准静态体系下计算损伤结构力-位移特征，这就需要将包含高动能船撞模型中的结构损伤特征引入无动能准静态计算体系，其中高动能损耗与局部强损伤必然导致巨大的计算成本（模型稳定过程）与收敛困难（模型奇异性），以至于目前对风电结构碰撞受损后剩余强度变化的研究较少。本文采用船舶-风电结构-土体全耦合模型，利用预定义场实现了动态与准静态计算有效转换，建立了完好结构极限强度、船撞结构损伤与受损结构剩余强度一体化计算体系，以工程实建单桩风机为对象，获得了船撞过程与受损结构剩余强度的关联关系。

1 结构模型和材料参数模型

1.1 风电结构模型和材料参数模型

本次研究选用海上风电大直径深桩（单桩）基础，单机容量6 MW。风电支撑结构由桩基、过渡段和塔筒组成，其几何参数如表1所示，风电整体（桩基和塔筒）结构采用S355低碳钢，其参数见表2。

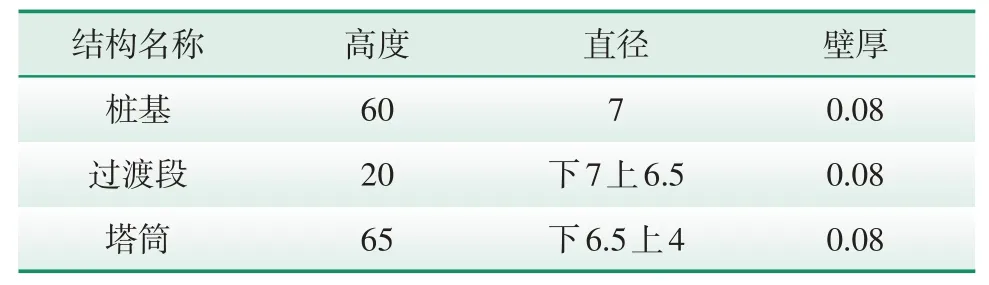
表1 风电单桩基础结构几何参数Tab.1 Geometric parameters of offshore wind turbine structure m

表2 低碳钢S355钢属性参数1）Tab.2 Parameters of steel properties in mild steel S355 specification

风电单桩基础结构几何模型如图1所示。桩基和塔筒采用渐变段设计建模，塔筒以上设备（机舱、轮毂、叶片等）通过RP点（耦合点）等效耦合在塔筒最高点，将该点设置为集中质量点，质量370 t。

图1 风电支撑结构几何模型Fig.1 Geometric model of monopile foundations

风电单桩基础和塔筒结构的材料为弹塑性硬化材料，具有线弹性的特征，其本构采用DNVGL-RP-C208《Determination of structural capacityby non-linear finite element analysis methods》[10]推荐的弹塑性硬化模型，该模型具有屈服平台的幂律硬化模型参数。该材料本构真实应力-应变关系可以定义为：

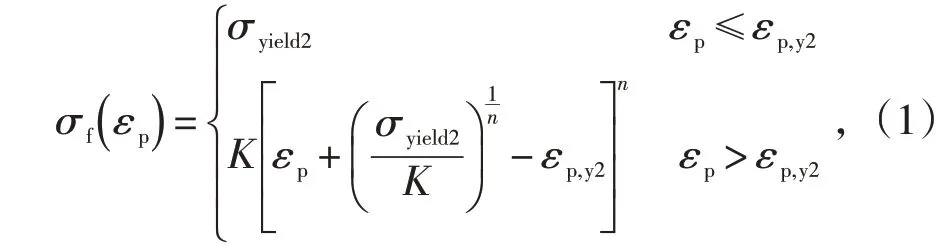
式中：σf为应力；εp为应变；n为硬化系数，取值0.166。

该材料本构关系（真实应力-应变）曲线见图2。

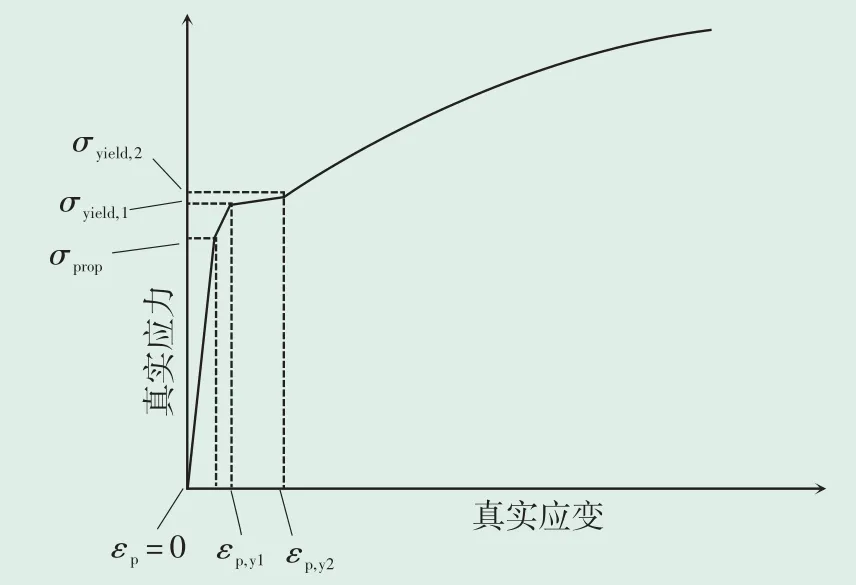
图2 材料本构真实应力应变曲线Fig.2 Constitutive true stress-strain curves of materials

材料损伤模型采用延性金属损伤中韧性损伤模型。损伤演化方向利用塑性断裂位移来控制，用线性形式表示损伤变量随塑性位移的增加而增加，当塑性位移达到断裂位移时，断裂发生，损伤变量D=1。断裂位移输入的参数值根据单元特征长度和厚度以及不同的单元类型输入。Kulzep和Peschmann[11]根据仿真研究给出了不同单元厚度的断裂应变（断裂位移）与单元特征长度的关系，如图3所示。

图3 最大断裂应变与单元大小的关系Fig.3 Relationship between maximum fracture strain and unit size

1.2 土体结构模型和材料参数模型

土体直径为120 m，高为75 m，中间桩留下的空隙为直径7 m，深度55 m。一般土体建模时要求土体直径为桩直径的20～40倍，为了提高计算效率，直径采用120 m。土体材料采用Mohr-Coulomb塑性模型，材料参数如表3所示。

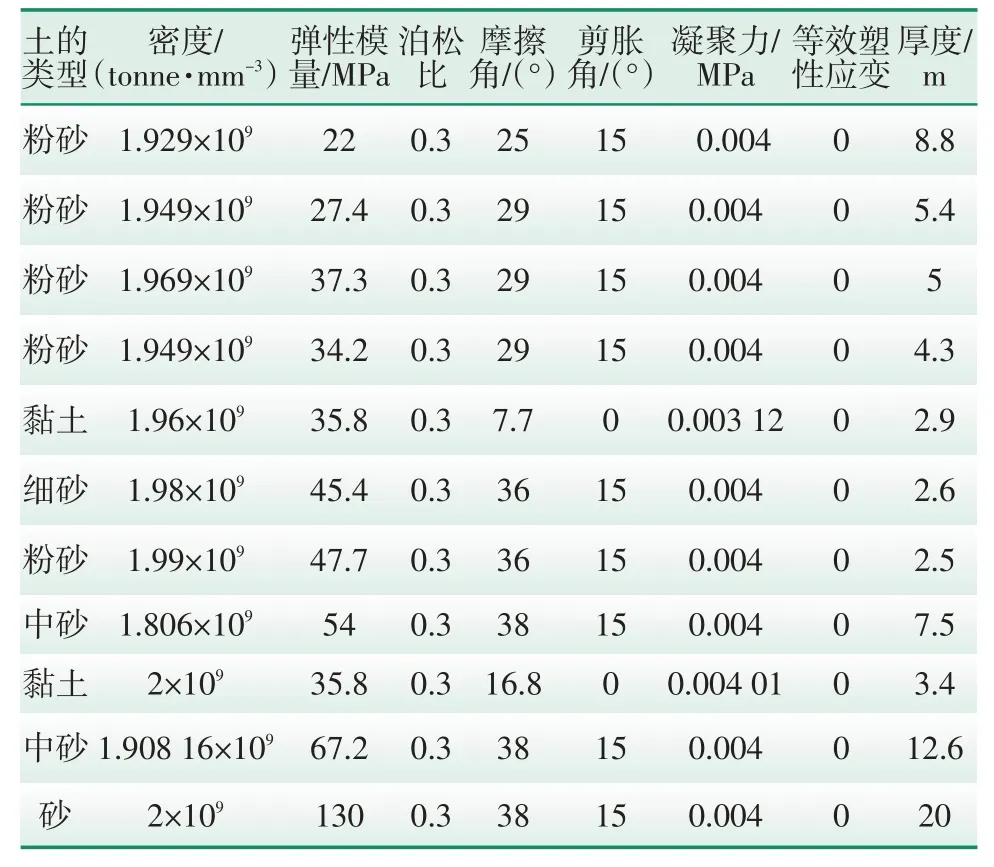
表3 模型中不同类型土体材料主要参数Tab.3 Main parameters of different types of soil materials used in the model

岩土工程分析中初始地应力是重要的影响因素之一，利用ABAQUS软件可以实现初始地应力平衡，土体分层几何模型见图4。

图4 土体分层模型Fig.4 Soil stratification model

1.3 船体结构模型

DNV GL-OS-A101[12]规范指出，碰撞能量根据典型船只计算，船侧碰撞一般不低于14 MJ，船艏和船尾碰撞不低于11 MJ。对于船舶碰撞能量E计算公式为：

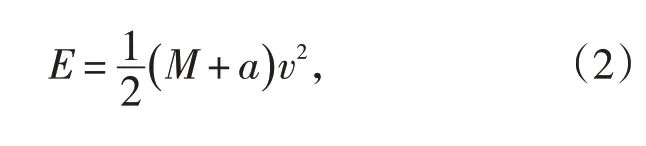
式中：M为船舶排水量，t，通常船侧碰撞为0.4M，船艏和船尾为0.1M；a为船舶附加质量，t；v为碰撞速度，m/s。

本研究基于船体结构的弹塑性材料及结构内部的分布特征进行模拟计算，建立船体模型。利用有限元软件MSC.Patran建立全尺寸船舶有限元数值模型。选用载重量为38 000 t、船体外体结构自重为5000 t，带有球鼻的艏散货船，集中质量点总质量为1800 t，机电设备及其上层建筑为2200 t，总自重共9000 t，船总长为185.8 m，垂线间长170 m，船舶型宽为31 m，型深15.43 m。设计吃水9.5 m，结构吃水10 m。

有限元网格划分节点和单元类型如下：总共402 844个节点，414 949个单元，57 000个两节点线性梁单元，12 229个两节点三维桁架单元，286 102个四结点双弯薄壳或厚壳单元，59 618个三节点三角形单元。船体整体有限元和碰撞部位局部网格细化模型如图5所示，船体材料模型和风电结构采用低碳钢S235，相关参数如表4所示。断裂应变、应力三轴度、应变率采用相应钢材料试验测得，损伤演化方向和断裂位移选取值与风电结构模型相一致。

图5 船体整体有限元和碰撞部位局部网格细化模型Fig.5 Overall finite element model of the hull and the local mesh refinement model of collision site

表4 低碳钢S235钢属性参数Tab.4 Parameters of properties of mild steel S235

2 含桩-土作用单桩基础整体结构极限强度分析

塔筒及其以上设备受力（包括结构自重）按照IEC 61400-3 International Standard[13]简化至桩基过渡段最高法兰盘截面中心点处的三个方向集中力和三个弯矩。首先采用简化方法处理桩基与土体之间的接触问题，采用Tie绑定约束接触方式。设置参考载荷3000 N，作用在桩基过渡段最高点处桩体表面耦合截面中心，方向沿水平X轴正方向。

2.1 未考虑塔筒及其以上结构分析

利用弧长法求解得到桩基过渡段最高点处水平荷载-水平位移曲线如图6所示。可见开始时曲线表现为线性特征，单桩基础结构处于弹性阶段，曲线的斜率即刚度；当力继续加载，曲线表现为非线性特征，单桩基础结构进入弹塑性阶段，曲线达到拐点处，单桩基础结构达到极限状态。由于桩体结构是弹塑性硬化材料，拐点之后加载很小力就会发生较大位移，曲线的斜率值即刚度不断变化。由图6可知，单桩基础结构水平极限承载力为60 MN，由图7可以看出单桩基础结构已经发生局部屈曲，土由体还未进入塑性状态。

图6 弧长法求解得到水平荷载-水平位移曲线Fig.6 Curve of horizontal load and horizontal displacement obtained by arc length method

图7 基础结构应力云图和土体S11(X)方向的应力云图Fig.7 Stress cloud diagram of foundation structure and soil S11 direction

利用准静态法对单桩基础结构进行极限强度研究。准静态法以结构非线性运动方程的显式求解为基础，运动方程如下：

式中：{P}为载荷列阵；{I}为内力矩阵；M为质量矩阵；{ü}为加速度矩阵。

首先利用弧长法得到水平位移为3.5 m时，水平承载力为76.232 5 MN进行加载分析，利用光滑幅值函数控制加载速度，保证加载过程不会产生加载速率变化引起的波动不连续行为。利用有限元软件ABAQUS中的频率分析步可以得到单桩基础结构的固有频率，进而求解其固有时间。通常采用单桩基础结构固有时间的10倍进行加载，充分保证得到精确静态解。通过分析可以得到结构的固有频率为0.751 05 Hz，准静态分析计算时间为13.31 s。

通过弧长法和准静态法分析得到水平荷载-水平位移曲线见图8，由图8可知准静态法求解结构的水平极限承载力为63 MN。准静态法相比弧长法得到的极限强度值略大，同时也验证了两种方法都是求解结构极限强度的有效方法。

图8 弧长法和准静态法分析得到水平荷载-水平位移曲线Fig.8 Curve of horizontal load and horizontal displacement obtained by arc length method and quasi-static method

对单桩基础结构进行弯矩加载分析，同样采用弧长法和准静态法分别进行加载，弯矩的方向为绕Y轴正向施加，结果如图9所示。由图9可知，弧长法求解得到绕Y轴正向极限弯矩为1.28 kN·m，准静态分析得到的绕Y轴正向极限弯矩为1.3 kN·m。

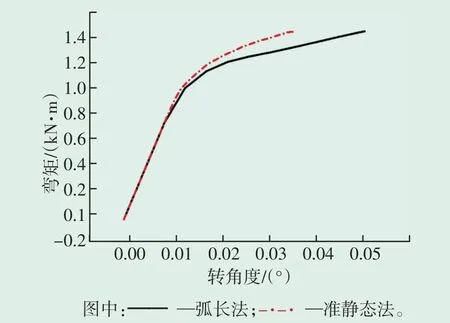
图9 弧长法和准静态法分析得到绕Y轴正向弯矩转角曲线Fig.9 Positive bending moment angle curve around Y axis obtained by arc length method and quasi-static method

可见，采用非线性弧长法和准静态法求解单桩基础结构水平极限强度，计算精度接近，而准静态法在非线性求解过程中处理收敛性问题上更有优势，将其确定为船撞单桩基础结构剩余强度求解方法。

2.2 整体结构分析

以上研究中未考虑塔筒及其以上结构，现对整体结构极限强度进行研究，利用准静态法进行求解，边界条件和施加荷载都与未考虑塔筒时相同，得到桩基过渡段最高点处水平荷载-水平位移曲线如图10所示。由图10可知，考虑塔筒及其以上结构求解得到极限承载力与未考虑时基本相同，故不考虑塔筒工况下利用准静态法求解极限强度对整体极限强度无影响。

图10 准静态法分析得到水平荷载-水平位移曲线Fig.10 Horizontal load and horizontal displacement curve obtained by quasi-static analysis

桩-土作用采用面与面接触，桩身是主面，土体内侧为从面。接触属性中的法向采用硬接触方式，接触属性切向方向摩擦方式采用动、静衰减系数模型，动、静摩擦系数为0.2，指数衰减系数为1。不同接触方式水平荷载-水平位移曲线对比见图11。风电整体应力云图和土体S11（X）方向应力云图见图12。由图12可以看出，桩土和土体应力主要集中在泥土面以下0～5 m。准静态法可以求解接触非线性问题，因此采用面与面接触更符合工程实际。

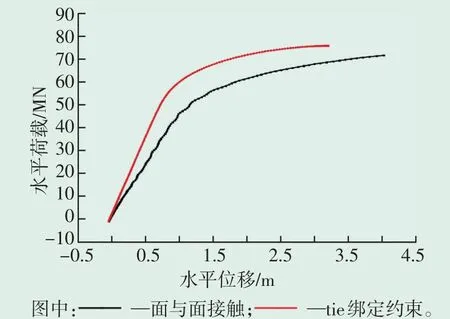
图11 不同接触方式水平荷载-水平位移曲线对比Fig.11 Comparison of horizontal load-horizontal displacement curves of different contact modes

图12 风电整体应力云图和土体S11（X）方向的应力云图Fig.12 Stress cloud diagrom of wind power and soil S11 direction

通过以上研究可以得出求解整体极限强度需要考虑的各种因素，包括两种不同求解极限强度的方法、集中力和弯矩加载分析、是否考虑塔筒及其以上结构分析、不同的桩-土之间接触方式等。

3 船舶碰撞海上风电基础分析

本研究采用显式有限元分析软件ABAQUS/Explicit进行碰撞分析。求解动力平衡方程时对时间积分采用中心差分法。

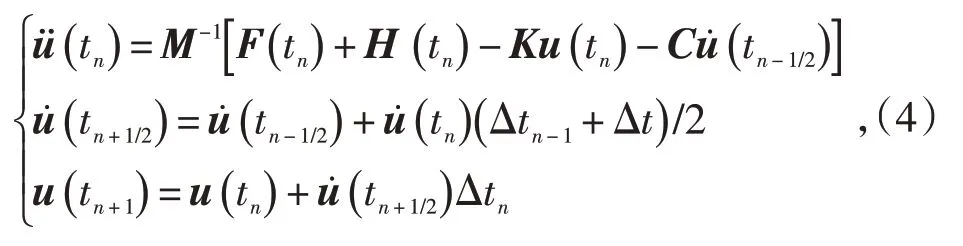
其中，tn-1/2=(tn+tn-1)/2,tn+1/2=(tn+1+tn)/2，

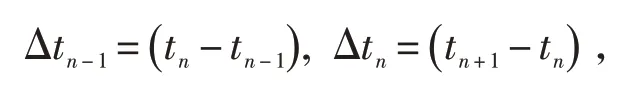
式中：C为阻尼矩阵；K为刚度矩阵；H为沙漏黏性阻尼力矩阵；u为位移向量；为tn时刻节点加速度，分别为tn、tn+1/2、tn-1/2时刻节点速度，u(tn+1)为tn+1时刻节点位移；M为有效质量矩阵；F为碰撞载荷，则F(tn)为tn时刻有效荷载。如果已知u(tn)和u(tn+1/2)就可求解u(tn+1)，然后计算出M和F，最后求出。

不同速度的碰撞场景如下：船体质量为9000 t（包含附加质量，附加质量系数0.05），速度分别选择4 m/s、3 m/s、2 m/s，正碰，水深17.3 m，吃水深度9 m，桩基直径7 m，桩基和塔筒厚度80 mm，塔筒最高点集中质量370 t，正碰不计摩擦系数，土体参数不变，土体和风机整体施加重力，水压力0.17 MPa，初始地应力作为土体初始条件，桩土作用部分切向方向采用罚函数公式，摩擦系数0.4。

船舶-风电-土体耦合碰撞整体有限元模型如图13所示。碰撞过程中采用质量缩放功能提高求解效率。碰撞力-凹陷位移曲线见图14，从图中可以看出速度越大，碰撞产生凹陷位移越大，回弹位移也越大；刚开始碰撞属于弹性碰撞，不同碰撞速度下斜率基本相同，随后进入弹塑性阶段，曲线表现出较强的非线性不稳定波动特征，碰撞力每次达到峰值后卸载都是接触重新建立和消失，主要是由船艏构件或桩体的受损失效破坏所致。

图13 船舶-风电-土体耦合碰撞整体有限元模型Fig.13 Overall finite element model of ship-wind power-soil coupling collision

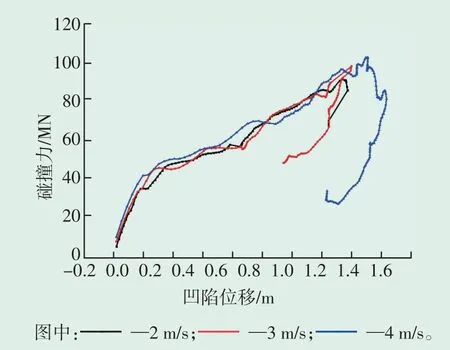
图14 不同速度碰撞下碰撞力-凹陷位移曲线Fig.14 Striking force-hollow displacement curve under collision with different velocities

图15是不同速度碰撞下风电整体结构和船体损伤等效塑性应变云图，可以看出船体球鼻艏部位产生了较大损伤，船甲板产生的损伤较小。图16是4 m/s速度下桩体整体变形和应力云图，碰撞过程在桩基过渡段产生了局部凹陷，在桩基嵌入土体表面下2.2～17.8 m中会发生局部弯曲挠度，在此区域内也产生损伤。图17为4 m/s碰撞下土体等效塑性应变和位移云图，可以看出，土体表面区域出现塑性应变，土体产生塑性破坏。

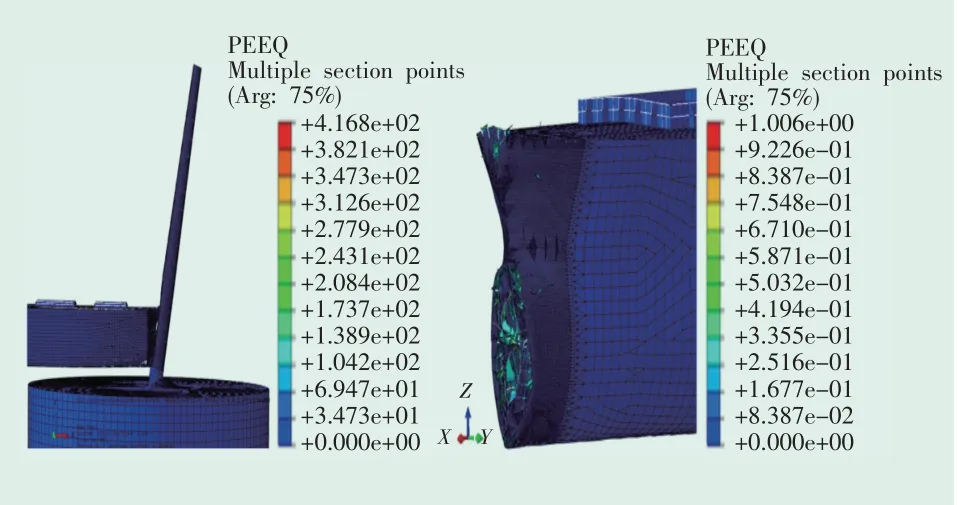
图15 4 m/s碰撞下整体和船体等效塑性应变云图Fig.15 Cloud diagram of the global and hull equivalent plastic strain under 4 m/s collision

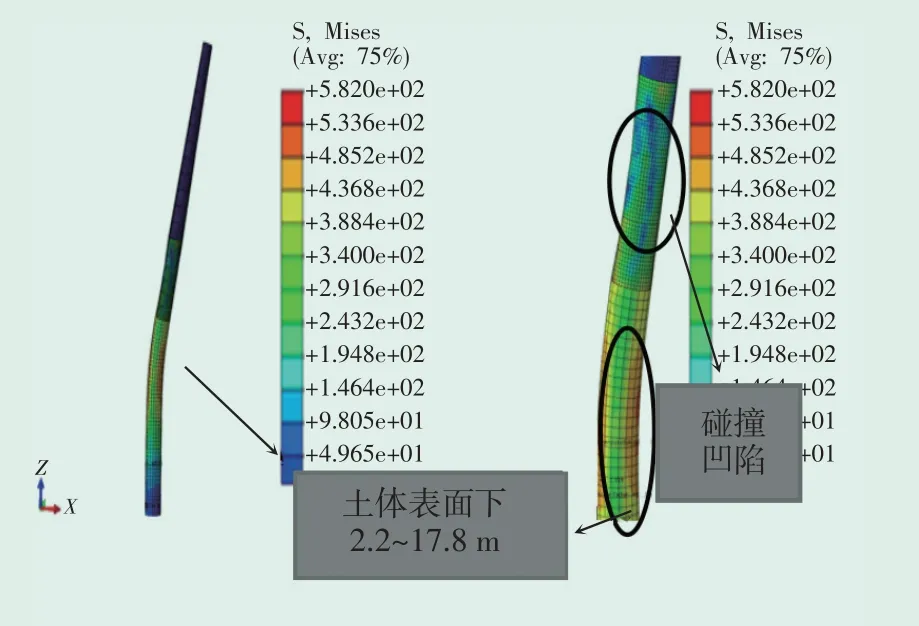
图16 4 m/s碰撞下风电整体和局部凹陷应力云图Fig.16 Stress cloud diagram of the whole and partial hollow of wind power under 4 m/s collision

图17 4 m/s碰撞下土体等效塑性应变和位移云图Fig.17 Cloud diagram of equivalent plastic strain and displacement of soil under impact of 4 m/s

4 船撞后单桩风电基础结构整体剩余强度分析

风电单桩基础结构遭受船舶碰撞后，会在碰撞后惯性力的作用下产生来回振荡，如果把碰撞的结果导入到下一步分析中会产生收敛问题或不稳定解，此时结构处于非静态或非准静态加载，导致结果出现偏差[14-15]。为了更符合工程特点，把单桩基础遭受船舶碰撞所得结果导入到动态衰减分析中，耗散掉弹性应变能，使得结构处于准静态工况下。动态衰减分析设置阻尼参数,使能量得以耗散，塔筒顶端振动幅度不断减小，然后把衰减分析得到的结果导入和传递到下一动态分析中，进行准静态加载并求解单桩基础结构剩余强度。

动态衰减分析时利用ABAQUS软件材料模块定义材料阻尼。ABAQUS/Explicit材料阻尼中使用Rayleigh阻尼参数设置。取前两阶频率来计算阻尼系数，结果为0.006 541。

选择不同碰撞速度下动态衰减后的损伤应力状态，将动态衰减分析的结果导入到下一步分析中进行剩余强度分析，利用准静态法进行求解，使用面与面接触方式，载荷和边界条件等其他设置或参数按照基础结构整体极限强度进行分析。通过对不同碰撞速度的损伤分析得到结构损伤程度，研究载荷施加方向、载荷施加考虑计算效率和模型求解复杂性。选择碰撞速度分别为4 m/s、2 m/s进行损伤分析，沿碰撞方向即X轴正向施加力表示为力+，反碰撞方向即X轴负向施加力表示为力-，绕Y轴正向施加弯矩表示为弯矩+，绕Y轴负向施加弯矩表示为弯矩-，施加不同方向力水平荷载-水平位移曲线见图18。表5和表6是不同速度下不同加载方向得到的剩余极限承载力/弯矩。

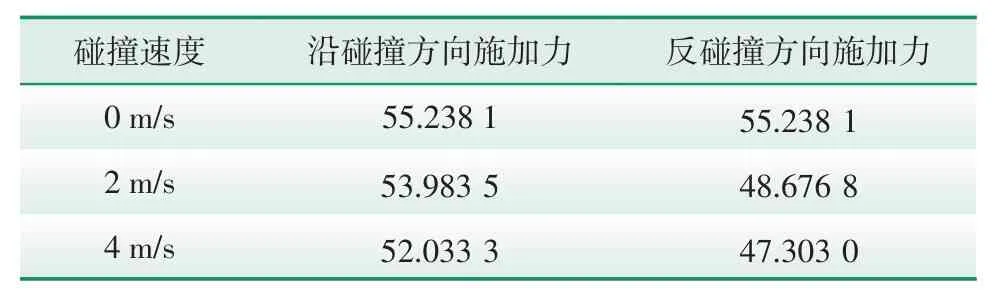
表5 不同碰撞速度作用下剩余极限承载力Tab.5 Residual ultimate bearing capacity under action of different collision velocities MN

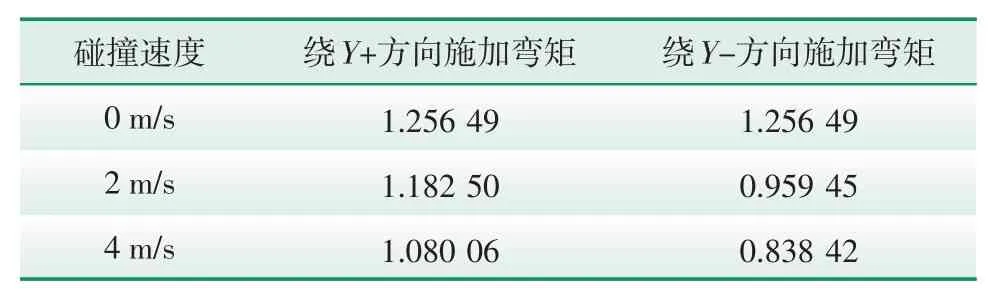
表6 不同碰撞速度作用下剩余极限弯矩Tab.6 Residual ultimate bending moments under different collision velocities MN·m

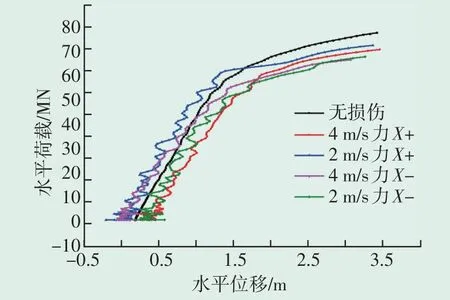
图18 施加不同方向力水平荷载-水平位移曲线Fig.18 Horizontal load-horizontal displacement curves with different direction forces applied

图19是碰撞速度为3 m/s下基础结构受损后求解剩余强度整体变形应力云图和桩基等效塑性应变云图。从图中可以看出不同荷载加载方式和加载方向下，其整体变形和桩基等效塑性应变的变化规律。当施加X轴正向力时，风电整体会在桩基嵌入土体表面下2.2～17.8 m中继续发生局部弯曲挠度，导致该区域等效塑性应变增加，损伤增大，结构承载能力下降，但并未在球鼻艏碰撞凹陷区域发生较大损伤。当施加X轴反向力时，风电整体在桩基嵌入土体表面下2.2～17.8 m处先发生回弹，然后继续沿X轴负向方向发生剪切受损，等效塑性应变增大；在碰撞凹陷区域也会发生剪切受损，等效塑性应变增大。当施加绕Y+方向弯矩时，风电整体在桩基嵌入土体表面下2.2～17.8 m处不发生变化，而是在桩基过渡段发生损伤，等效塑性应变增大。当施加绕Y-方向弯矩时，风电整体会在桩基嵌入土体表面下2.2～17.8 m处发生回弹，但损伤并未增大；在碰撞凹陷区域会发生较大剪切损伤，导致凹陷区域继续增大，直至压缩破坏。

5 结论

海上风电单桩基础结构遭遇船舶碰撞前后整体极限强度会发生明显变化。船舶碰撞过程中是高能量结构之间相互传递过程，涉及各种非线性的叠加，本文提出船舶-风电结构-土体全尺寸耦合模型，采用非线性有限元求解法能够高效处理以上过程，现得出以下结论。

（1）对于风电整体极限强度分别采用非线性弧长法和动态显式（准静态法）求解。两类方法计算精度接近，准静态法在非线性求解过程中处理收敛性问题上更有优势，同时也可以考虑桩-土接触摩擦阻力的影响，利用准静态法分析剩余强度。

（2）船舶碰撞涉及各种非线性问题，采用动态显式求解程序能更好地求解碰撞过程。当采用不同速度碰撞时，速度越大，最大凹陷位移越大，回弹量也越大。碰撞开始时属于弹性碰撞，不同碰撞速度下碰撞力-凹陷位移斜率即结构刚度相同，随后进入弹塑性阶段，曲线出现较强的非线性特征。碰撞损伤不仅出现在桩基与船艏（球鼻艏和甲板）接触凹陷部位，而且还出现在桩基嵌入土体表面下2.2～17.8 m中发生局部弯曲挠度区域，且该区域相比碰撞凹陷部位的损伤较大，同时土体也会产生塑性损伤。

（3）进行受损后剩余极限强度研究，首先需要进行动态衰减能量分析，以避免出现波动不稳定特征。针对不同速度碰撞受损后承载性能曲线，可以看出单桩基础结构承载能力有所降低；对碰撞后施加不同的荷载形式或荷载方向其持续发生损伤的区域不同，当施加集中力时，损伤主要在桩基嵌入土体表面下2.2～17.8 m处累积，当施加弯矩时，损伤主要在碰撞凹陷处累积。