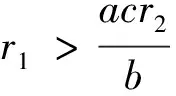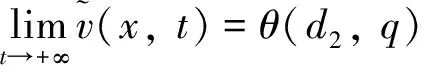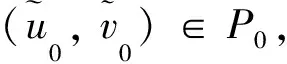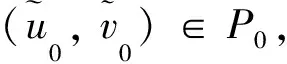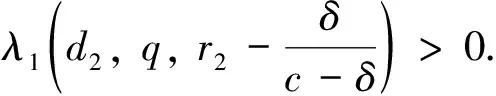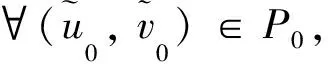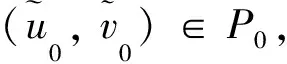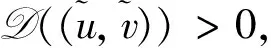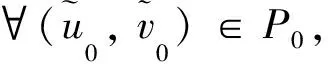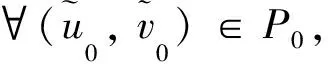对流环境下具有额外食物资源的Leslie-Gower捕食者-食饵模型①
杨旺,张国洪
西南大学 数学与统计学院, 重庆 400715
捕食者和食饵之间的相互作用是自然界中最常见的现象之一,长期以来受到生态学家和数学家的广泛关注.文献[1-2]提出了各种类型的捕食者-食饵模型, 并研究了其动力学行为.特别地, Leslie提出了如下Leslie-Gower捕食者-食饵模型[3-4]:
(1)

文献[7]在模型(1)的基础上建立了具有随机扩散的Leslie-Gower捕食者-食饵模型,其动态结果和模型(1)类似,即系统的唯一正平衡点是全局稳定的[8].除了随机扩散,许多物种还可能向某个方向定向迁移,如在对流环境(如河流)中被单向流动的水流推动等.近年来,越来越多的学者开始研究河流生态系统中单向水流的冲刷作用对种群的动态影响[9-10].综合上述讨论,本文建立如下对流环境下修正的Leslie-Gower捕食者-食饵模型:
(2)
这里d1,d2是相应的扩散速度,q是捕食者受到的对流速度,l表示河流长度,均为正常数.其他变量和参数与模型(1)的意义相同.u0(x)和v0(x)分别表示食饵与捕食者的初始分布.这里我们假设模型(2)中的捕食者进行包含随机扩散和定向迁移的混合运动,而食饵进行纯粹的随机扩散,这种情况在生态学中是有可能发生的,例如食饵是常居于河底的藻类植物(此处的流速为0),而捕食者是常居于流速不为0区域的食藻类生物. 由于食饵只进行随机扩散,边界条件ux(0,t)=ux(l,t)=0表示没有食饵会通过边界.捕食者的边界条件d2vx(0,t)-qv(0,t)=vx(l,t)=0表示上游为无流的边界(即没有个体通过上游),下游为自由流的边界条件(表示下游个体离开水域的速度和流速相同,例如溪流进入湖泊).在本文中,我们总是假设d1,d2,r1,r2,c,a,b,q皆为正常数,并且河流长度为固定值l=1.
为了研究模型(2)的动力学行为,首先考虑在没有食饵(即u≡0)的情况下, 模型(2)所对应的如下单物种模型:
(3)
模型(3)的动力学行为由如下线性特征值问题决定:
(4)
由Krein-Rutman定理易知, 特征值问题(4)存在单的主特征值λ1(d2,q,r2)和对应的严格正的特征函数φ1(d2,q,r2). 根据文献[11]的引理2.2(b)和文献[12]的引理2.2,可得如下的两个结论,其在后文将对模型(2)的理论分析发挥重要作用:
引理1设d2,r2,q>0,存在唯一的q*>0,这里的q*由λ1(d2,q*,r2)=0唯一确定,使得当0
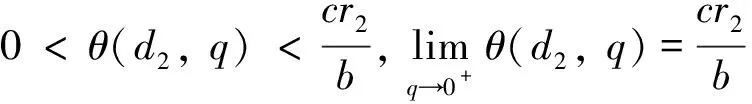
1 模型的耗散性
定理1对于给定的初始条件,存在正常数ρ1和ρ2, 使得模型(2)的解满足0 证根据文献[13], 可知模型(2)的解局部存在且唯一.故接下来只需证明解的有界性.由极大值原理可知u(x,t)>0,v(x,t)>0.结合模型(2)中关于u的方程可得 ut≤d1uxx+u(r1-u) 0 令V(x,t)满足 因此存在一个只依赖于初值u0(x)和v0(x)的正常数ρ2, 使得0 易得模型(2)总是存在边界平衡态解(0, 0),(r1, 0). 当0 定理2模型(2)的灭绝平衡态解(0, 0)总是不稳定的. 证模型(2)在(0, 0)处线性化后对应的特征值问题为 (5) 由引理1知,特征值问题(5)第一个方程的主特征值λ1(d1, 0,r1)=r1>0, 因此模型(2)的平衡点(0, 0)总是不稳定的. 定理3当0 证首先证明平衡点(r1, 0)的局部稳定性. 考虑模型(2)在(r1, 0)处线性化后的特征值问题 (6) 定义Λ是特征值问题(6)的谱, 显然Λ=Λ{ψ=0}∪Λ{ψ≠0}.当ψ=0时,考察特征值问题 d1φxx-r1φ=λφ0 (7) 易知问题(7)的主特征值λ1(d1, 0, -r1)=-r1<0. 因此对特征值问题(7)的特征值λ都有Reλ≤λ1<0, 则sup{Reλ:λ∈Λ{ψ=0}}<0.当ψ≠0时,考察特征值问题 (8) sup{Reλ:λ∈Λ{ψ=0}∪Λ{ψ≠0}}>0 (r1, 0)不稳定.若q>q*,则问题(8)的主特征值λ1(d2,q,r2)<0, 因此 sup{Reλ:λ∈Λ{ψ=0}∪Λ{ψ≠0}}<0 (r1, 0)局部渐进稳定. 现在证明平衡点(r1, 0)是全局吸引的. 由极大值原理易知u(x,t)>0,v(x,t)>0. 且根据定理1知 (9) 故对任意ε>0, 存在T1>0, 当t>T1时,u(x,t) ut≥d1uxx+u(r1-aε-u) 0 考虑方程 (10) 因此(r1, 0)是全局吸引的, 故(r1, 0)全局渐进稳定. 注1定理3表明总存在一个流速阈值q*,使得当模型(2)的流速大于该阈值(即q>q*)时, 平衡态解(r1, 0)总是全局稳定的.这意味者流速较大时,捕食者灭绝,而食饵存活. 接下来,我们考虑流速较小,即0 定理4设0 证模型(2)在(0,θ(d2,q))处线性化后的特征值问题为 (11) 同样地, 定义Λ′是特征值问题(11)的谱, 则Λ′=Λ′{ψ=0}∪Λ′{ψ≠0}. 当φ=0时,考察特征值问题 (12) 因此sup{Reλ:λ∈Λ{φ=0}}<0. 故特征值问题(11)主特征值的正负将由φ≠0时的特征方程 (13) (14) (15) 在这一节中,我们使用一致持续性理论来研究模型(2)的一致持续性条件,相关理论的详细介绍可以参见文献[15-16]. (16) 的解. 由比较原理, 当t≥t0时, Ws((0, 0))∩D-1(0, +∞)=∅Ws((r1, 0))∩D-1(0, +∞)=∅ Ws(0,θ(d2,q))∩D-1(0, +∞)=∅2 边界平衡态解的稳定性
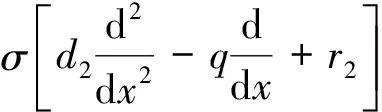
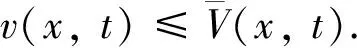

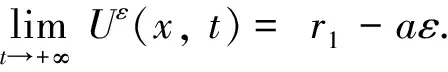
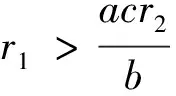
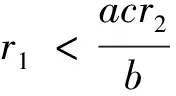
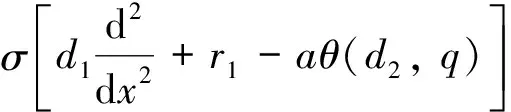

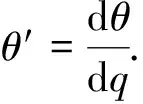
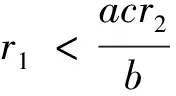
3 模型的一致持续性