基于改进磷虾群算法的主动配电网无功优化

高金兰, 宋 爽, 王良禹, 刁 楠, 侯学才

(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)

0 引 言

随着配电网技术的不断创新与完善, 光能、 风能等可再生分布式电源在配电网中被广泛应用[1-2]。分布式电源(DG: Distributed Generations)能将大量的有功功率输送给配电系统, 同时还可传输一定的无功功率, 使DG具有无功补偿调节的能力, 并在参与无功补偿时具有经济成本低、 补偿具有连续性、 补偿速度快等优点[3-4]。但随着分布式电源大量加入配电系统, 由此产生的并网给配电网的总体优化以及容量补偿调节带来了相当大的困难。主动配电网通过主动控制和主动管理技术使网络具有更加灵活地控制电能以及主动消纳可再生分布式能源的能力, 从而使整个配电系统具有较高的安全性与稳定性[5]。主动配电网无功优化中, 除了考虑在配电网中加入电容器组(CB： Capacitor Banks)、 传统有载调压变压器(OLTC： On Load Tap Changing)以及静止无功补偿装置(SVC： Static Var Compensator)等措施外, 还应该考虑DG无功调节的能力对配电网运行的影响, 目的是为在减小系统网络损耗的同时降低对配电系统电压稳定性的影响[6]。

目前, 国内外的专家已针对该问题进行了许多相关的讨论与研究。首先是模型构建方面, 黄伟等[7]充分考虑光伏出力的不确定性, 将光伏出力作为一种参与无功容量调控以及系统调压的手段； 董雷等[8], 任佳依等[9]和颜湘武等[10]将模型预测控制策略与动态无功优化相结合, 应用这种方法不仅能加强配电网在运行过程中对各变量的优化控制, 而且还能提高配电系统的稳定性与可靠性。然而, 上述研究未考虑到负荷及分布式能源出力的预测误差以及补偿设备的离散和连续性。其次是求解算法方面, 刘欣雨[11]和滕德云等[12]分别采用了蚁群算法和鲸鱼算法对无功模型进行求解； 高远等[13]则采用人工神经网络与遗传算法相结合的方法。然而, 以上算法在处理动态无功优化方面具有容易陷入局部最优, 不可行解难以解决等问题。

针对当前主动配电网无功优化存在的典型问题, 笔者提出基于改进磷虾群算法的多时间尺度无功优化策略。首先建立基于最小网损和最小电压偏差的多目标模型, 将优化过程分为日前调控与日内动态补偿两部分, 日前为考虑离散型设备的小时级无功优化, 日内为考虑SVG(Static Var Generator)和风光出力的日内分钟级优化。其次提出一种改进的磷虾群算法, 将余弦控制因子和柯西因子引入磷虾群算法, 可在提高算法全局搜索能力的同时, 有效地避免磷虾群算法后期产生局部最优的可能性, 引用Sobol序列将种群初始化, 使初始磷虾群多样性大幅提升。最后通过修正的IEEE33节点系统, 验证了提出的主动配电网多时间尺度无功优化策略的可行性和有效性。

1 多时间尺度无功优化

主动配电网多时间尺度无功优化分为日前调控和日内实时无功调节两部分, 基本框架如图1所示。在日前优化阶段, 基于日前预测的负荷及新能源有功出力数据, 优化调节未来24 h每小时的离散型补偿设备, 以实现有功网损和电压偏移量最小化两个目标。日内实时调节时域取15 min, 以日前调动方案为基准, 以实现在负荷及新能源出力实时波动下, 控制新能源无功出力, 使系统电压维持在合理水平的同时减小网损。其中在日内优化层, 充分考虑到风光的无功出力, 结合SVG的动态无功补偿能力, 对系统进行无功补偿, 使电压趋近于理想水平。

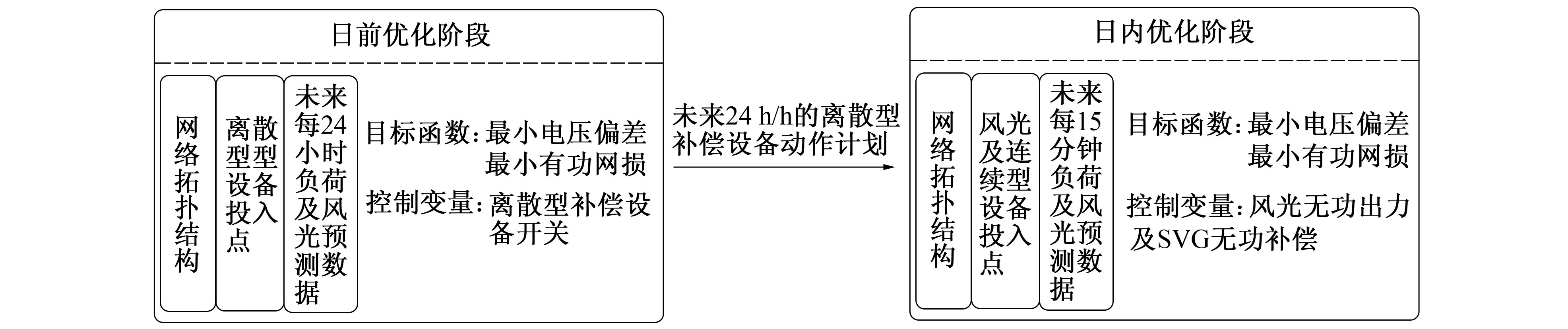
图1 多时间尺度协调的无功优化框架Fig.1 Multi-time scale coordinated reactive power optimization framework

2 多时间尺度无功优化模型

2.1 日前无功优化控制模型

第1阶段以配电网运行经济性和电压水平稳定性为期望, 将预测得到的未来24 h风光和负荷的数据作为输入变量, 以并联电容器组档位作为控制变量, 将1 h作为日前优化计算的间隔, 根据电网的初始运行状态, 求解离散型补偿设备未来24 h各个小时的最优调节方案。

2.1.1 目标函数

日前小时级无功优化以有功网络损耗和节点电压偏差值最小化作为目标函数。

1) 有功网损最小化

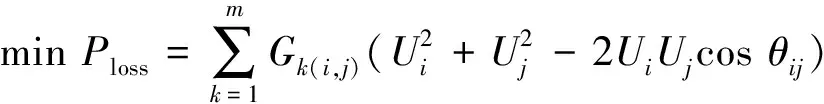
(1)

其中Ploss为有功网损；Ui和Uj分别为节点i和节点j的电压幅值；Gk(i,j)和θij分别为节点i和节点j之间的电导和相位差;m为支路总数。

2) 电压偏量最小化

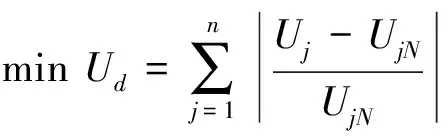
(2)

其中Ud为电压偏差；Uj为节点j的实际电压；UjN为节点j的额定电压;n为节点总数。

3) 目标函数归一化。对上述目标函数进行归一化处理并构建目标函数, 则有

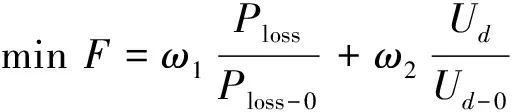
(3)

其中Ploss-0和Ud-0分别为无功优化前的有功网损和电压偏差；ω1和ω2分别为上述两个指标的权重系数。笔者将权重进行随机分配,ω1为0～1范围内的随机生成数,ω1+ω2=1, 以确保所得解的多样性。

2.1.2 约束条件

1) 潮流方程约束

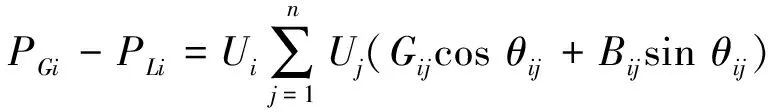
(4)

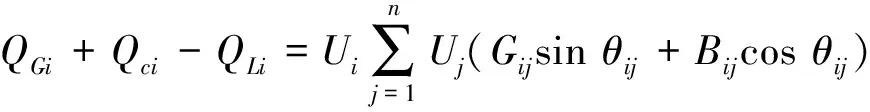
(5)

其中PGi和QGi分别为发电机和分布式电源注入系统的有功功率和无功功率；PLi和QLi分别为系统中负荷所消耗的有功功率和无功功率；Qci为无功补偿装置所投入的无功功率；Gij和Bij分别为节点i和节点j之间的电导与电纳。

2)节点电压约束

Vimin≤Vi≤Vimax

(6)

其中Vi为节点的电压幅值；Vimin和Vimax分别为节点电压幅值的上限和下限。

3) 装置出力约束

QC,d,imin≤QC,d,i≤QC,d,imax

(7)

其中QC,d,i为节点d处的并联电容器装置补偿容量；QC,d,imax和QC,d,imin分别为节点d的并联电容器装置补偿容量的上限和下限。

2.2 日内无功优化控制模型

第1阶段日前无功优化后, 已确定离散型补偿装置未来24 h的最优补偿调节策略, 第2阶段在第1阶段最优设定值的基础上, 以电压偏移量最小和网损最小为目标进行分钟级实时调节SVG和风光出力, 使实时电压平稳运行。日内优化目标与日前的目标保持一致, 其目标的归一化处理也相同, 这里不再赘述。潮流方程约束和节点电压约束也与上述相同。

光伏、 风电和SVG无功出力约束为

其中Qpvi,Qpvimin,Qpvimax分别为节点i的光伏无功功率及其最小值与最大值；Qptj,Qptjmin,Qptjmax分别为节点j的风电无功功率及其最小值和最大值；QSVGi为第i个SVG的无功输出大小；QSVGimin和QSVGimax为第i个SVG的无功输出最小值和最大值。

3 基于改进磷虾群算法的动态无功优化

3.1 磷虾群算法

Gandomi等[14]首先提出了磷虾群算法, 其为通过观察磷虾种群的日常行为特征而设计的一种群体智能优化算法。其初始的种群分布是随机的, 个体迭代的过程主要受附近磷虾群的诱导、 觅食行为、 随机物理扩散3个方面的共同影响。

磷虾群的运动数学模型可用n维决策空间中的拉格朗日模型表示

(11)

其中Ni为附近磷虾群的影响；Fi为觅食行为；Di为第i个磷虾个体的随机扩散行为, 则有

其中Nmax、Vf和Dmax分别为最大诱导速度、 最大觅食速度和最大扩散速度,α、β、δ分别为诱导方向、 觅食方向和扩散方向,wn,wf分别为觅食权重和诱导权重,t、tmax分别为当前迭代次数和最大迭代次数。

磷虾个体在t到t+Δt区间的位置更新公式为

(15)

其中Δt为速度向量的缩放因子,Ct为步长缩放因子, 取[0,2]区间的常数,NV为变量数,UBj,LBj分别为第j个变量的上界和下界。

3.2 磷虾群算法改进

考虑到无功优化模型有动态性, 多约束性等特点, 常规的磷虾群算法不能在优化时域发生变化时充分利用历史种群及历史最优解信息, 并且不能随着环境的变化快速构建初始种群, 为此, 笔者通过以下3方面对磷虾群算法进行改进。

3.2.1 基于Sobol序列的种群初始化

Mirjalili等[15]提出了解决可行解分布不确定等问题, 初始种群数据的分布应尽可能地均匀分布在数据空间中, 这不仅使种群能拥有较高的多样性, 而且还能增强解集的可靠性。传统的磷虾群算法采用随机数形式产生初始磷虾个体, 这种方法不能将初始磷虾个体均匀地分布在求解的数据空间中。随机分布可能使最优解附近种群分布稀疏, 进而影响计算效果和计算效率, 而且种群的过度聚集也将导致局部最优情况。采用Sobol序列可产生超均匀分布粒子, 改善初始磷虾群多样性, 使磷虾个体均匀地分布在空间中。

Sobol序列生成初始磷虾群方法如下

xi=xmin+λ(xmax-xmin)

(16)

其中xmax,xmin分别为磷虾位置上下限,λ为Sobol序列生成的位于[0,1]范围内的随机数。

3.2.2 引入余弦控制因子

由式(12)和式(13)可看出, 诱导运动权重wn和觅食行动权重wf对磷虾个体的运动影响很大, 笔者提出一种觅食权重和诱导权重的余弦递减策略, 提高算法的全局搜索力, 如下

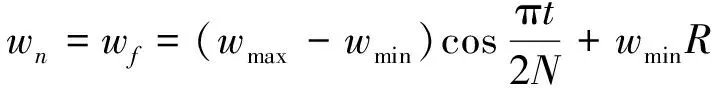
(17)

其中t为当前迭代次数,N为最大迭代次数,wmax和wmin分别为诱导权重以及觅食权重的最大值与最小值。前期w权重值偏大, 可使算法更好地进行全局搜索。并且, 随着迭代次数的不断增多,w权重值逐渐减小, 此时会进行更小范围的精细搜索。随机数R的引入不但可以提高w的随机性, 使改进后的算法能有效地适应搜索情况随时间的不断改变, 还可提高全局搜索能力。

3.2.3 引入柯西变异因子

传统的磷虾群优化算法具有容易早熟以及陷入局部最优等缺点。针对这些问题, 笔者在研究磷虾个体的位置更新时, 通过引入柯西变异因子, 减少磷虾个体进入局部最优的可能性。主要原理为： 通过柯西变异因子对潜在的最优磷虾个体进行局部区域的大面积搜索, 在具有一定的潜在最优解的范围内产生随机干扰, 即可有效地增加磷虾群算法的局部搜索能力[16]。柯西变异概率密度函数如下

(18)

其中x0为位置参数,γ为一个大于0的随机变量,x为一个实数。笔者取x0=0,γ=1, 以其为标准的柯西分布规律。通过对其概率密度函数的分析, 可知其均值与方差是没有特定值的, 但众数以及中值都等于位置参数, 即x0。其分布函数如下

(19)

引用柯西变异因子改进扰动公式如下

xibest(t)=xi(t)+xi(t)G(x)

(20)

(21)

其中f(xi(t))为磷虾i在第t次迭代时的适应度值。通过引用柯西变异因子, 使改进后的磷虾群算法跳出局部最优。

3.3 基于改进磷虾群算法的主动配电网无功优化

将改进后的磷虾群算法应用于主动配电网无功优化模型求解过程中, 笔者提出的基于改进磷虾群算法的主动配电网无功优化求解流程如下。

Step 1 输入日前各项参数, 风光负荷预测数据, 并联电容器的补偿容量约束等；

Step 2 设置优化时域时段数为N, 最大迭代次数为Gmax, 总时段为T, 按照sobol序列初始化t时段种群；

Step 3 生成初始磷虾群的位置x、 计算适应度值并记录最佳磷虾的位置和适应度值f；

Step 4 进入迭代, 计算虚拟食物中心的位置xfood和敏感邻域半径ds,j, 并不断更新食物中心位置；

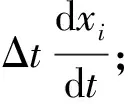
Step 6 执行扰动算子, 更新磷虾位置和适应度值；

Step 7 如果满足终止条件(迭代次数), 输出日前优化阶段最优解, 否则返回Step3；

Step 8 将得到的最优日前控制方案数据导入日内阶段, 输入日内各项参数, 按上述改进磷虾群算法求解步骤进行求解, 得到最终的优化结果。

4 算例分析

4.1 算例参数

笔者利用Matlab编辑软件对改进后的IEEE 33节点配电系统进行仿真计算分析, 具体系统结构如图2所示。

在IEEE 33配电系统中, 基准值的选取为SB=10 MV·A；UB=12.66 kV。在6,7,24,32节点处分别接入无功补偿并联电容器投切装置, 最大投切容量为0.6 MVar。在3,29节点处接入SVG, 容量均为0.2 MVar。10,22,30节点接入光伏发电机组, 投入容量分别为2台0.3 MW, 1台0.4 MW。在17,27节点接入风力发电机组, 投入容量分别为0.6 MW和0.4 MW。其中风光出力预测曲线及负荷预测曲线如图3所示。

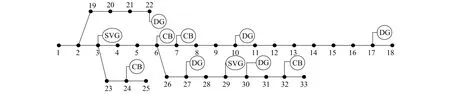
图2 修改的IEEE 33节点系统图Fig.2 Modified IEEE 33 node system diagram

4.2 仿真结果分析

4.2.1 日前无功优化结果分析

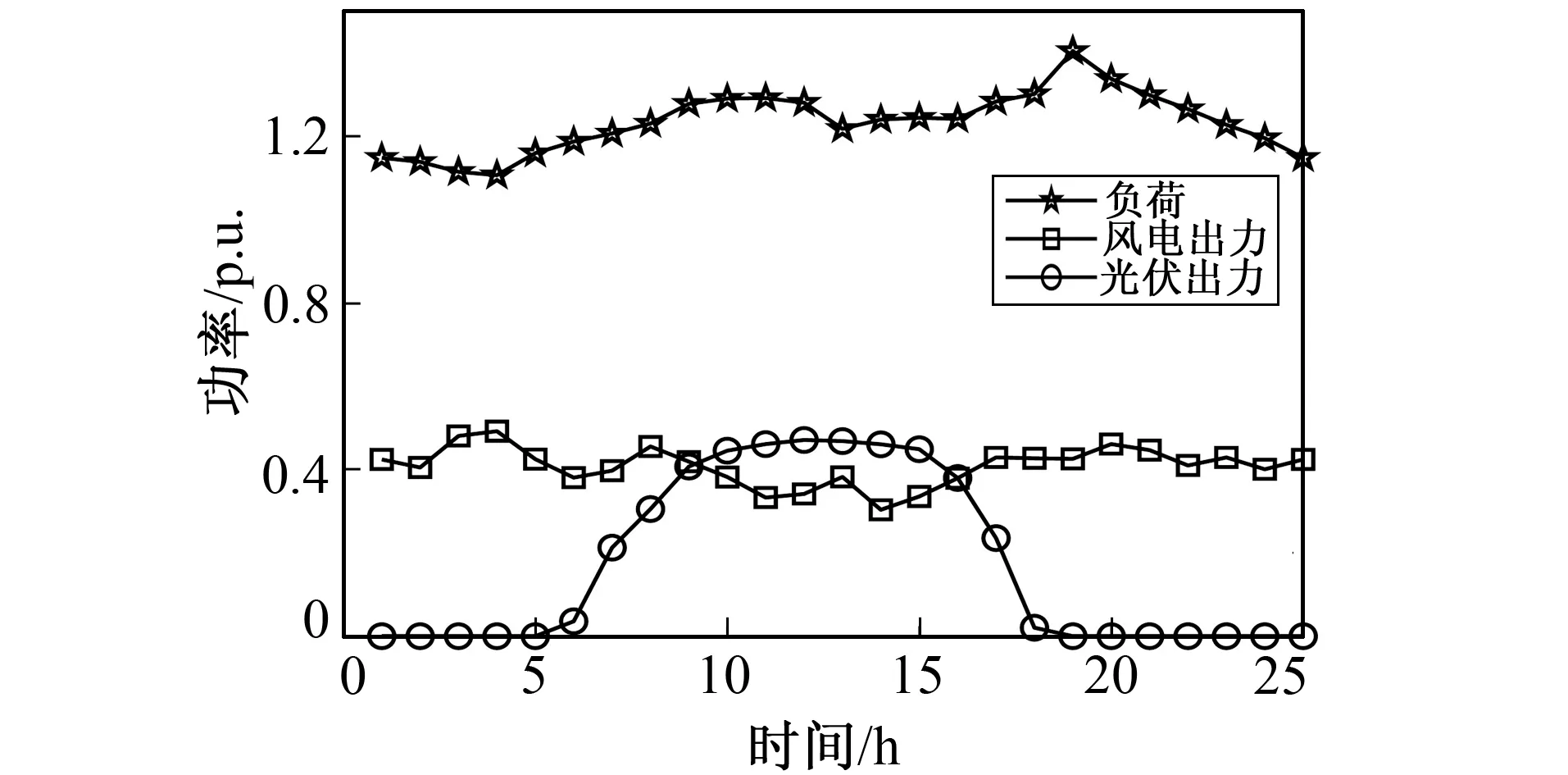
图3 风光出力及负荷变化图Fig.3 Wind power output and load variation diagram

日前无功优化方案后的电压和网损如图4, 图5所示。由图4可看出, 日前优化前, 系统整体的电压水平较低, 一部分节点靠近0.92 p.u., 个别节点甚至低于0.92 p.u.。经过日前优化方案调节, 总体电压部分趋于平稳, 一部分节点电压得到提升, 大部分节点的电压可达到0.94 p.u.以上, 还需配合日内进行无功优化。

由图5可看出, 通过日前阶段优化, 确定离散型设备无功调节方案, 可使网损有一定程度的降低。总网损由5 892 kW下降至3 475.2 kW, 总体降低41%。其中第19 h网损由351.8 kW降至217.6 kW, 降幅为38.1%。

图4 日前无功优化电压对比图 图5 日前无功优化网损对比图 Fig.4 Comparison diagram of day-ahead reactive power optimization voltage Fig.5 Comparison diagram of day-ahead reactive power optimization network loss

4.2.2 日前日内无功优化结果分析

图6,图7为日内优化前后每个时段的电压分布。可以看出, 经过日前日内综合优化后, 电压水平整体上升, 电压质量有明显改善。

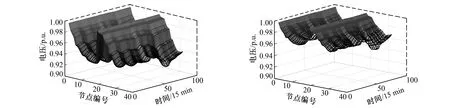
图6 日内优化前各时刻电压分布 图7 日内优化后各时刻电压分布Fig.6 Voltage distribution at each time before intra day optimization Fig.7 Voltage distribution at each time after intra day optimization

为进一步说明笔者提出的基于改进磷虾群算法日前日内两阶段动态无功优化策略的有效性, 将日前日内两阶段优化后的电压水平和网损大小与仅日前优化结果进行对比, 如图8和图9所示。

图8为选取其中一个典型时刻电压水平进行分析对比的结果。图9为日内优化后与仅日前优化的网损对比结果。

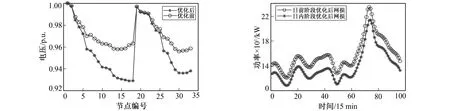
图8 日内优化后与日前优化后电压对比图 图9 日内优化后与日前优化后网损对比图Fig.8 Voltage comparison diagram after ntra day optimization and day-ahead optimization Fig.9 Network loss comparison diagram after intra day optimization and day-ahead optimization i

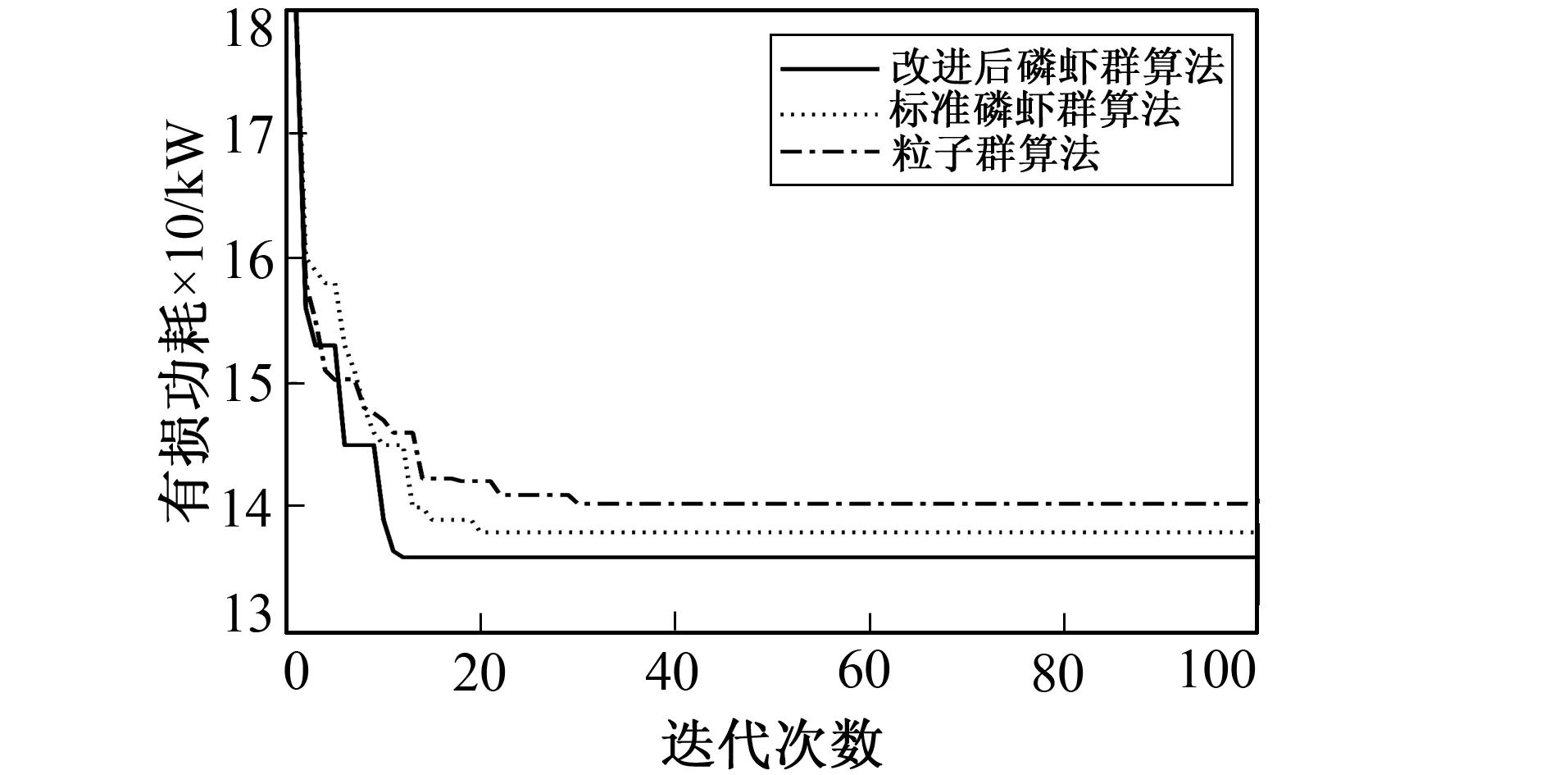
图10 3种算法无功优化收敛曲线Fig.10 Three algorithms optimize convergence curves of reactive power

由图8可看出, 随着分布式能源及SVG的无功补偿的加入, 电压水平有了较明显的改善。仅采用日前阶段优化时, 节点电压波动较大, 仍然会出现越限情况。采用日前日内两阶段优化策略, 可将电压控制在合理的运行区间, 各节点电压均达到0.95 p.u.以上, 其中最低电压由0.929 p.u.提升至0.956 p.u.。进行日内优化后, 整体网损有了进一步降低, 在各个时刻均有一定程度的减少。可看出, 通过日前日内两阶段的优化可有效地减小网损, 进而提高经济效益。

4.2.3 算法性能分析

将笔者提出的改进磷虾群算法与标准磷虾群算法、 粒子群算法相比较, 收敛曲线运行结果如图10所示。可以看出, 标准磷虾群算法和粒子群算法分别需迭代20次和30次左右, 而笔者提出的改进磷虾群算法迭代12次左右就可以达到最优解。因此, 改进后的磷虾群算法的全局寻优能力更强, 收敛速度更快。

5 结 论

1) 笔者建立了基于有功网损和电压偏移量最小化的无功优化模型。在算例分析中可看出, 进行日前离散设备的无功调节后, 电压偏移和有功网损均有降低, 但效果不明显。

2) 日内充分考虑SVG和风光的无功出力参与后, 网损和电压偏移都有很大程度的降低, 进一步保证了主动配电网运行的安全性和经济性。

3) 采用Sobol序列的对磷虾群进行初始化, 引用余弦控制因子和柯西变异因子对磷虾群算法进行改进。改进后的算法可以更好地提高全局搜索能力, 有效避免了陷入局部最优解, 在算例中也有良好的表现。笔者考虑了电压水平和网损的大小, 之后可对动作成本及其他目标做进一步的研究。

参考文献：

[1]康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架 [J]. 电力系统自动化, 2017, 41(9): 2-11.

KANG Chongqing, YAO Liangzhong. Key Scientific Issues and Theoretical Research Framework of High Proportion Renewable Energy Power System [J]. Power System Automation, 2017, 41 (9): 2-11.

[2]WANG Bing, WANG Qian, WEI Yiming, et al. Role of Renewable Energy in China’s Energy Security and Climate Change Mitigation: An Index Decomposition Analysis [J]. Renewable & Sustainable Energy Reviews, 2018, 90: 187-194.

[3]滕德云, 滕欢, 刘鑫, 等. 考虑多个分布式电源接入配电网的多目标无功优化调度 [J]. 电测与仪表, 2019, 56(13): 39-44.

TENG Deyun, TENG Huan, LIU Xin, et al. Multi Objective Reactive Power Optimal Scheduling Considering Multiple Distributed Generators Connected to Distribution Network [J]. Electrical Measurement and Instrumentation, 2019, 56(13): 39-44.

[4]寇凌峰, 吴鸣, 李洋, 等. 主动配电网分布式有功无功优化调控方法 [J]. 中国电机工程学报, 2020, 40(6): 1856-1865.

KOU Lingfeng, WU Ming, LI Yang, et al Distributed Active and Reactive Power Optimal Regulation Method for Active Distribution Network [J] Chinese Journal of Electrical Engineering, 2020, 40(6): 1856-1865.

[5]丁港野. 主动配电网无功优化的算法研究 [D]. 南昌: 南昌大学信息工程学院, 2019.

DING Gangye. Research on Reactive Power Optimization Algorithm of Active Distribution Network [D]. Nanchang: School of Information Engineering, Nanchang University, 2019.

[6]杨德昌, 廖文龙, 孙雪, 等. 基于满意度阈值判定的主动配电网无功优化 [J]. 电网技术, 2017, 41(9): 3003-3010.

YANG Dechang, LIAO Wenlong, SUN Xue, et al Reactive Power Optimization of Active Distribution Network Based on Satisfaction Threshold [J]. Power Grid Technology, 2017, 41(9): 3003-3010.

[7]黄伟, 刘斯亮, 王武, 等. 长时间尺度下计及光伏不确定性的配电网无功优化调度 [J]. 电力系统自动化, 2018, 42(5): 154-162.

HUANG Wei, LIU Siliang, WANG Wu, et al. Optimal Reactive Power Dispatch of Distribution Network Considering Photovoltaic Uncertainty in a Long Time Scale [J]. Power System Automation, 2018, 42(5): 154-162.

[8]董雷, 陈卉, 蒲天骄, 等. 基于模型预测控制的主动配电网多时间尺度动态优化调度 [J]. 中国电机工程学报, 2016, 36(17): 4609-4617.

DONG Lei, CHEN Hui, PU Tianjiao, et al. Multi Time Scale Dynamic Optimal Dispatching of Active Distribution Network Based on Model Predictive Control [J]. Chinese Journal of Electrical Engineering, 2016, 36(17): 4609-4617.

[9]任佳依, 顾伟, 王勇, 等. 基于模型预测控制的主动配电网多时间尺度有功无功协调调度 [J]. 中国电机工程学报, 2018, 38(5): 1397-1407.

REN Jiayi, GU Wei, WANG Yong, et al. Multi-Time Scale Active and Reactive Power Coordinated Dispatching of Active Distribution Network Based on Model Predictive Control [J]. Chinese Journal of Electrical Engineering, 2018, 38(5): 1397-1407.

[10]颜湘武, 徐韵, 李若瑾, 等. 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化 [J]. 电工技术学报, 2019, 34(10): 2022-2037.

YAN Xiangwu, XU Yun, LI Ruojin, et al. Multi-Time Scale Reactive Power Dynamic Optimization of Distribution Network with Renewable Distributed Generation Based on Model Predictive Control [J]. Journal of Electrotechnics, 2019, 34(10): 2022-2037.

[11]刘欣雨. 基于蚁群算法的配电网无功优化研究 [D]. 西安： 西安石油大学电子工程学院, 2020.

LIU Xinyu. Research on Reactive Power Optimization of Distribution Network Based on Ant Colony Algorithm [D]. Xi’an: School of Electronic Engineering, Xi’an Shiyou University, 2020.

[12]滕德云, 滕欢, 刘鑫, 等. 基于改进鲸鱼优化算法的多目标无功优化调度 [J]. 电力电容器与无功补偿, 2019, 40(3): 123-128,136.

TENG Deyun, TENG Huan, LIU Xin, et al. Multi-Objective Reactive Power Optimization Dispatch Based on Improved Whale Optimization Algorithm [J]. Power Capacitor & Reactive Power Compensation, 2019, 40(3): 123-128,136.

[13]高远, 丁璐, 纪洁. 基于遗传算法和人工神经网络算法的新型无功优化混合算法 [J]. 电子测试, 2020(13): 47-49,76.

GAO Yuan, DING Lu, JI Jie. Hybrid Algorithm for Reactive Power Optimization Based on Genetic and Artificial Neural Network Algorith [J]. Electronic Test, 2020(13): 47-49,76.

[14]GANDOMI A H, ALAVI A H. Krill Herd: A New Bio-Inspired Optimization Algorithm [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(12): 4831-4845.

[15]MIRJALILI S, GANDOMI A H. Chaotic Gravitational Constants for the Gravitational Search Algorithm [J]. Applied Soft Computing Journal, 2017, 53(4): 407-419.

[16]PENG G, FANG Y, PENG W, et al. Multi-Objective Particle Optimization Algorithm Based on Sharing-Learning and Dynamic Crowding Distance [J]. Optik, 2016, 127(12): 5013-5020.