一类性质没有Hermitian矩阵优但比一般矩阵良的矩阵

田咏梅，刘慧娟，王 超

(郑州商学院 通识教育中心，河南 巩义 451200)

0 引言

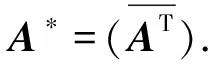
1 基本结果

定理1设A∈Cn×n,A*=A4,则

(1)A是正规矩阵.

(2)A的谱是下述集合

(1)

的子集，且该矩阵具有以下奇异值分解

其中，U,V均为n阶酉矩阵，Ir是r阶单位矩阵.

(3)A的属于不同特征值的特征向量正交.

证明：(1)因为A*=A4，以及

A*A=(A4)A=A(A4)=AA*,

(2)

所以A为正规矩阵，A可以和对角矩阵酉相似.

(2)设λ=a+ib,a,b∈R是A的一个特征值, 则有向量x,0≠x∈Cn,使得

Ax=λx.

(3)

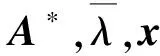
(4)

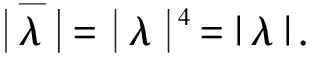
|λ|1=1,|λ|2=0.

对于|λ|1=1,在(4)式两边同乘以λ，得到

(5)

这时对方程1=λ5,使用德·费弗公式，得A的诸特征值如下.

(6)

对于|λ|2=0⟹λ=0.因此,任何适于条件A*=A4的矩阵A的谱满足下述关系：

由于矩阵A是正规矩阵，其特征值的模即为其奇异值，所以，矩阵A的奇异值为1或0.于是，存在n阶酉矩阵U,V，使得

(7)

这便是矩阵A的奇异值分解式.其中的子矩阵Σr=Ir，这是一般矩阵所难以企及的.这种矩阵的奇异值分解式在线性分析理论、最小二乘问题、广义逆矩阵、实验数据处理等方面都有重要应用[7].

(3)设λ,μ是矩阵A的任意两个不同特征值，非零向量α,β分别是对应的特征向量.根据酉空间向量内积的概念，有

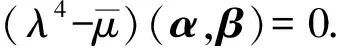
为了下面推导A的行列式与逆矩阵表示式时叙述方便，我们取A的所有可能的特征值是λ0,λ1,λ2,λ3,λ4,λ5=0，且设它们的重数依次为a0,a1,a2,a3,a4,a5.

定理2设A∈Cn×n,A*=A4,则

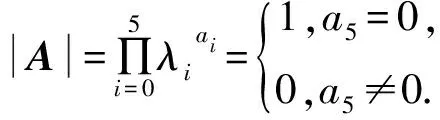
(2)当a5=0时，有酉矩阵U，使得

A=U*ΛU=U*diag[1,…,1,λ1,…,λ1,…,λ4,…,λ4]U，

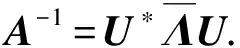
证明：(1)由定理1，满足本定理条件的矩阵的可能特征值是0及诸λs,s=0,1,2,3,4，由于λs都是方程λ5=1的零点，而此方程又是实系数方程，故其复根应成对出现.实际上，经验证知

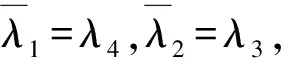
(8)

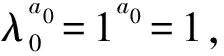
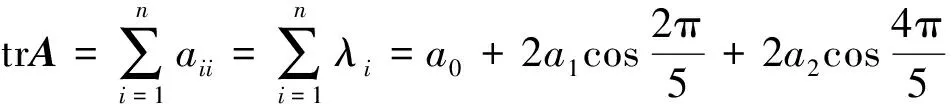
(2)由定理1，A为正规矩阵，意味着它可以和对角矩阵酉相似，即存在酉矩阵U使得

A=U*ΛU=U*diag[1,…,1,λ1,…,λ1,…,λ5,…,λ5]U.

(9)

其中，λ0,λ1,λ2,λ3,λ4,λ5都是矩阵A的特征值，Λ=[1,…,1,λ1,…,λ1,…,λ5,…,λ5].这样当a5≠0时，A不存在逆矩阵；当a5=0时，A的所有特征值全不为零，(9)式中不再存在λ5，因而A存在逆矩阵.将(9)式两边取逆，并利用式(8)，有

(10)

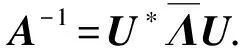
A-1=U*diag[1,…,1,λ4,…λ4,λ3,…,λ3,…,λ1…,λ1]U.

(11)

进一步地，由AadjA=|A|I=I，还可以推得

A-1=adjA.

(12)

综合上面的讨论，我们得到矩阵A的逆的三种形式分别由(10)(11)(12)式给出.

关于矩阵A的一些说明：一方面，它有一些性质比一般矩阵好.

1)一般矩阵，都存在一个正整数m使得

r(Am)=r(Am+1)=r(Am+2)=…

(13)

这里，r(B)表示矩阵B的秩.但满足定理1的条件的矩阵A，这个正整数m可以是1.

事实上，对于任意的正整数m，利用(9)式有

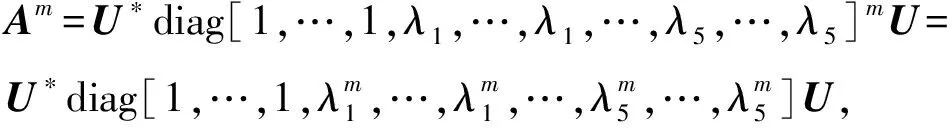
这表明(13)式中的m可以是1，即

r(A)=r(A2)=r(A3)=…

(14)

2)设a0,a1,a2,a3,a4,a5的意义同定理2前面的约定.一般矩阵A∈Cn×n满足

(15)

但利用(8)式，我们有

这里‖A‖F为Cn×n上的Frobenius矩阵范数((15)式中的“≤”可以是“=”).

除了上面列举和证明的结果，还有许多优点，这里就不一一赘述了.

另一方面，Hermitian矩阵是矩阵理论与应用中一类重要的矩阵，解析函数插值理论等领域被广泛应用，Hermitian矩阵的特征值全为实数，本文中的矩阵的特征值可能是复数.这一点关系重大，因为在一些重大工程技术中，只有整数特征值才能够考虑被使用，而任何非整数,特别是复数特征值的应用都需要谨慎. Hermitian矩阵还有许多本文中的矩阵A所不可企及的优势.但是，如果在某些科学技术、工程技术、经济研究等问题中，无缘遇到Hermitian矩阵，而遇到本文中的正规矩阵时，这类矩阵将被派上用场.另外，在一些理论研究中，哪些问题的条件可以由Hermitian矩阵替换成本文中的正规矩阵，尚需进一步研究.

2 结语

本文证明了适于条件A*=A4的矩阵A∈Cn×n是正规矩阵，给出了它的谱、奇异值分解式与逆矩阵表示式.当正规矩阵仅有实数特征值时，这种矩阵就变成了Hermitian矩阵，其将具有Hermitian矩阵所具有的所有优良性质.