多目标数学规划下的监控网络测点数据传输仿真

杨自香

(芜湖职业技术学院 信息与人工智能学院,安徽 芜湖 241006)

当今社会,监控网络的布设和使用已成为城市建设和管理的重要一环。例如,在交通管理方面,通过监控可随时查看违规车辆以及事故追溯;在社会安全方面,通过监控可以实时追踪犯罪嫌疑人;在商场超市方面,通过监控可以防止商品丢失,降低商品失窃率[1]。监控网络主要由监控中心和监测点两部分组成,前者主要用于显示监控画面以及远程控制监测点,后者主要布设在现场,用于拍摄现场画面,通过无线通信网络将数据传输给监控网络。随着监控范围的扩大,监控设备越来越多,在避免监控漏洞的同时,也给数据传输带来巨大压力,监控网络的测点数据传输性能逐渐无法满足需求,经常出现严重的数据丢包、延迟等问题。面对上述情况,优化监控网络数据传输可靠性和效率具有重要的现实意义。

目前,有许多关于数据传输性能的优化研究,如田夏利[2]构建了网络数据采集模型,基于传播网络利用数据特征优化参数,实现网络数据传输优化;杨艳琦[3]设计了基于树型 分簇型拓扑的数据高效传输优化算法,考虑网络节点的剩余能量、节点数量、节点间隔距离等因素,构建传输簇和数据传输最优路径,降低了数据传输的平均延迟。以上数据传输性能优化方法取得了一定的成果,但是所构建的目标函数普遍是围绕一个目标,导致求取的传输方案只能满足一方面的传输性能优化需求。

针对上述问题,为了全面提升监控网络数据多目标传输的可靠性、传输时延以及传输能耗,对多目标数学规划下的监控网络测点数据传输仿真进行研究。考虑传输可靠性、传输时延以及传输能耗建立多目标函数,设置约束条件,并构建数据传输多目标规划模型;利用改进遗传算法求取规划模型最优解,获得监控网络测点数据最优传输方案。通过该研究可提高数据传输综合性能,为监控网络的升级和改造提供参考和借鉴。

1 监控网络测点数据传输多目标数学规划模型

测点在监测到数据之后,通过监控网络将数据远程传输到监控中心。受带宽以及信道资源的限制,多个测点数据会同时争抢一份网络资源,时常会导致数据损坏或数据丢失现象。面对这种情况,构建一种监控网络测点数据传输多目标数学规划模型。该模型构建主要分为3部分,即模型假设条件设定、多目标数学规划模型构建以及模型约束条件设置。

1.1 模型假设条件设定

假设条件的作用是方便多目标数学规划模型的构建,简化多目标求解问题[4]。针对监控网络测点数据传输多目标数学规划模型,设置6个模型假设条件为:①监控网络的拓扑结构已知;②监控网络测点位置和数量已知;③监控网络中不存在冗余通信链路;④每个网络测点的监控数据量相同[5];⑤监控网络覆盖面积固定和已知;⑥测点发送一个数据包所消耗的能量是动态的[6]。

1.2 多目标数学规划模型构建

在上述假设条件下建立多目标数学规划模型,其由多个单目标函数、若干个约束条件组建而成[7]。模型基本结构如下:

式中:Y为n个目标函数组成的目标向量;yi(x)为第i个单目标函数;x为决策向量;n为目标函数的数量;A(x)为等式约束条件;B(x)为不等式约束条件。

参考上述多目标数学规划模型基本形式,针对监控网络测点数据传输问题,将传输可靠性、传输时延以及传输能耗等3个单目标组合在一起,构成多目标函数[8]。该函数表达式如下:

式中:F为综合目标最优值;minf1(x)为传输时延最小化目标;minf2(x)为传输能耗最小化目标;maxf3(x)为传输可靠性最大化目标;ω1为传输可靠性权重;ω2为传输时延权重;ω3为传输能耗权重。

(1) 传输时延最小化目标

式中:ai为第i个测点数据传输量;bi为第i个测点数据传输路径的信道带宽;ci为第i个测点数据传输路径丢包概率;di为第i个测点数据传输路径的安全系数;m为测点数据传输路径的数量;ui为可选信道[10]。

1.3 模型约束条件设置

为便于求解规划模型,设定求解范围,为上述建立的多目标函数设置约束条件[11]如下:

(1) 数据传输路径长度约束

式中:vmax为通信网络所能提供的最大数据传输速率;v为通信网络的实际数据传输速率;hi为接入的第i个监测点;N为监测点个数。

(4) 网络负载均衡性约束

(6) 非负约束。模型中出现的所有参量均为非负数。

2 求解监控网络测点数据传输方案

针对上述建立的监控网络测点数据传输多目标数学规划模型,利用一种寻优算法求解满足该模型的最优解[13]。最优解即监控网络测点数据的最优传输方案。传统遗传算法用于多目标函数的寻优时全局搜索和局部优化容易产生矛盾,探索能力强则易造成群体分散,不易收敛,而收敛能力强则易陷入局部极小点。本文选择的寻优算法为改进遗传算法,采用双群体同步寻优对传统遗传算法存在的缺陷进行改进[14]。双群体同步寻优是用两个群体分工协作,一个是全局群体操作,负责寻找存在最优点的区域,另一个是局部群体操作,负责搜索全局群体划定的区域,找到最优点。其优势在于可实现局部优化和全局优化的平衡,收敛能力更强。具体步骤如下:

步骤1 假设监控网络中监测点数量为τ,通信网络节点数量为n。

步骤2 种群初始化。在设置的6个约束条件范围内随机生成初始种群,并通过二进制编码方式对每个个体进行编码[15]。编码形式如下:

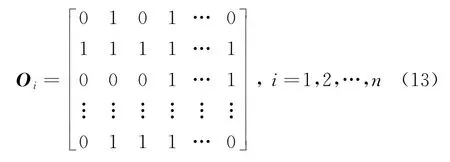
式中:Oi为第i个初始解。

步骤3 利用全局群体操作将初始种群划分为不可行解和可行解两个区域,由此形成两个种群记为ξ和ζ,两个种群的规模分别记为T1和T2。

步骤4 按照式(4)多目标函数计算种群中个体的适应度。

步骤5 判断适应度是否达到期望值。若达到则结束,输出最优解;否则,继续下一步。

步骤6 对种群进行变异和交叉操作,由此产生试验种群μ。在多目标优化过程中通常不存在同时最小化所有目标函数的可行解,为了增加多目标最小化效果,降低至少一个目标,使所有目标得到改进的不可行解,从而解决计算困境。因此,在变异操作中同时加入不可行解和可行解,实现全局和局部最优。经过变异操作产生的第i个试验个体表达式为

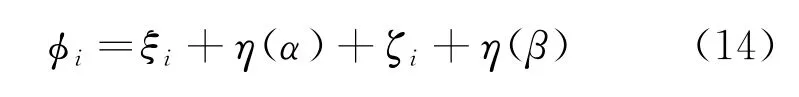
式中:ξi为不可行解种群中的第i个个体;ζi为可行解种群中的第i个个体;η为变异因子;α为搜索到的局部最优可行解;β为目前为止搜索到的全局最优可行解,即最优点区域。

局部群体操作是利用交叉操作从最优区域中找到最优解。交叉操作是遗传算法的核心环节,其原理为:自然界生物的染色体通过基因重组形成新的染色体,父代染色体的优良性状最大程度上遗传给下一代染色体,通过不断交叉遗传产生最优个体。经过交叉操作产生的第i个试验个体为

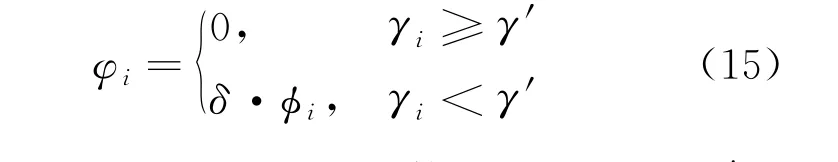
式中:γi为第i个变异试验个体的变异程度;γ′为设定的阈值;δ为交叉因子。

步骤7 从μ中筛选出不满足约束条件的个体,进行种群更新。

步骤8 按照式(5)～式(7)计算更新后种群中每个个体的单目标函数值。

步骤9 计算每个个体的聚合度。计算公式如下:

式中:λi为第i个个体的聚合度;f1(i)为传输时延聚合度;f2(i)为传输能耗聚合度;f3(i)为传输可靠性聚合度;σ为更新后群体规模。

步骤10 筛选出聚合度函数值最小的个体,该个体为最优解,是监控网络测点数据最优传输方案[16]。

通过上述过程,完成多目标数学规划下的监控网络测点数据传输优化研究。

3 仿真测试与分析

为测试研究方法的应用性和有效性,进行监控网络测点数据传输仿真实验。该实验以多目标函数求解下的传输方案为测试组,以3个单目标函数求解下的传输方案为对照组,即传输时延单目标函数求解方案为对照1组,传输能耗单目标函数求解方案为对照2组,传输可靠性单目标函数求解方案为对照3组。

根据实际的某市监控网络布设情况,选择在1 000 m(X轴)×1 000 m(Y轴)的范围内搭建仿真测试环境,如图1所示。

图1仿真测试环境相关参数如表1所示。仿真软硬件配置如表2所示。

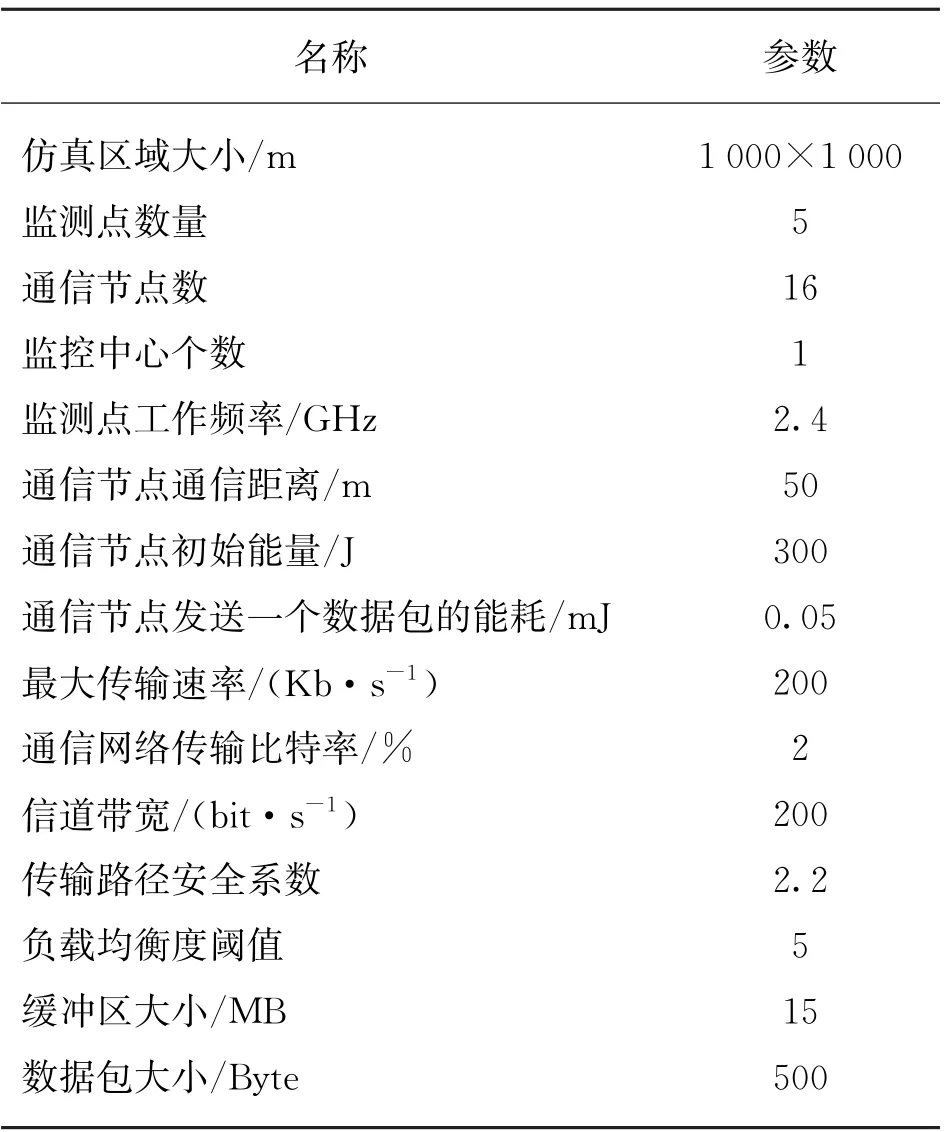
表1 仿真测试环境相关参数

表2 实验环境配置

图1 仿真测试环境

结合均值自适应法的思想原理,估计多目标函数较为合适的权值分配方法:ω1为0.563 1,ω2为0.210 8,ω3为0.226 1。

利用改进遗传算法求解目标函数,设置相关参数:种群规模为不可行解200,可行解200;最大迭代次数为200;适应度期望值为10;交叉因子为0.2;变异因子为0.3。根据上述参数,采用双群体同步寻优,进行变异和交叉操作,筛选出聚合度函数值最优解,获得监控网络测点数据最优传输方案。

对比测试传统遗传算法、文献[2]的改进粒子群算法和本文改进遗传算法的收敛速度,结果如图2所示。

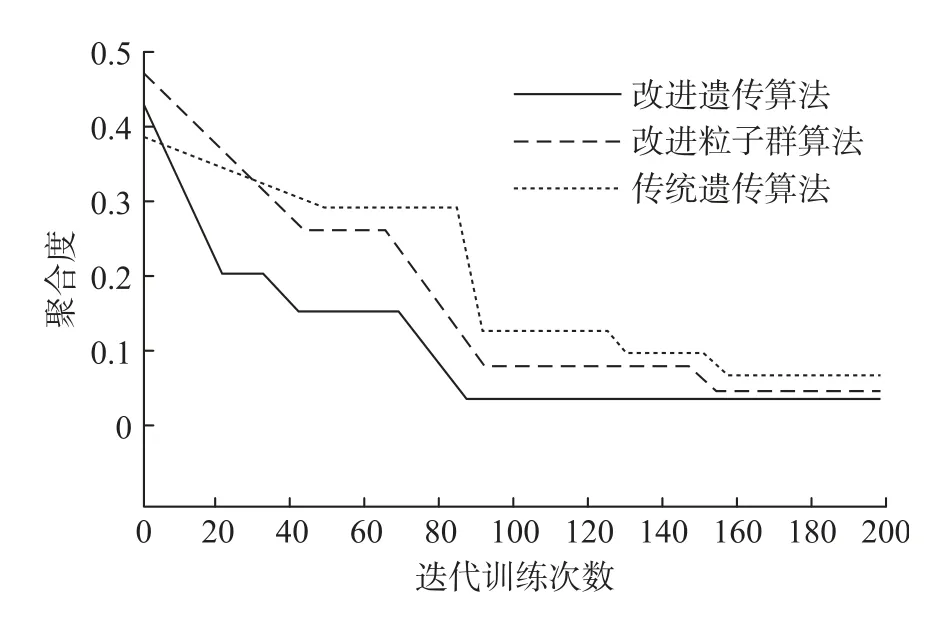
图2 算法收敛性测试结果

由图2可知,本文设计的改进遗传算法收敛速度最快,在迭代87次左右达到聚合度最低值,低于0.1,而其他算法均在140次之后才达到最优值且高于本文算法的聚合度。以上数据证明本文算法的寻优效率最佳。

利用改进遗传算法求取的传输方案如图3所示。对比每个传输方案的传输时延、传输能耗以及传输可靠性,判断传输方案性能,结果如表3所示。

图3 5个监测点的数据传输方案

由表3可知,测试组传输方案的时延虽然不如对照1组,能耗不如对照2组,可靠性不如对照3组,但是由于综合考虑了3个目标,综合性要远远好于3个对照组。对照组只考虑一个方面,往往导致一个方面非常好,但是其他方面非常差的情况发生,这与现实传输要求不符。现实中监控网络在传输时不可能只要求一方面性能,而忽视其他性能要求。

表3 传输方案的传输时延、能耗以及可靠性数值

4 结 语

随着监控测点数量的不断增加,监控范围扩大的同时,使得测点数据传输问题越来越严重。面对这种情况,进行多目标数学规划下的监控网络测点数据传输仿真研究。该研究将传输可靠性、传输时延以及传输能耗等3个单目标组合在一起,构成多目标数学规划模型,最后通过求解得出最优数据传输方案。经仿真测试,多目标函数求解方案比单目标求解方案的综合性更强,验证了本文研究方法的有效性。