极端灾害下考虑电网和天然气网络侧的综合能源系统弹性评估

罗 鹏, 刘永慧, 姚晓东

(上海电机学院 电气学院,上海 201306)

随着能源应用的发展速度加快,全球对能源的需求逐年增长。在此背景下,提出了能高效利用多种能源的电 气综合能源系统(Integrated Gas-Electric System,IGES)[1]。该系统能协同优化、综合管理电力和天然气的生产、输送、转换、储存、分配、消费。为保证IGES正常高效运行,有许多文献对IGES遭遇常规故障进行了可靠性分析,但对IGES在自然灾难、恶劣天气等极端灾害事件下造成的大面积故障事故的弹性分析较少,而极端灾害事件会造成IGES大面积的系统瘫痪,给系统带来灾难性打击[2]。

近年来,国内外对极端灾害下IGES弹性评估中的电网侧进行了研究,并取得了一定成果。文献[3]将复杂网络理论应用于IGES的鲁棒性分析,并调用平均聚类算法(G)计算网络特征参数,综合分析IGES在不同故障下的鲁棒性和系统薄弱环节。文献[4]利用N-1方法分析了各类控制模式下的电气 热能源系统静态安全性。文献[5]提出了“韧性电网”的概念,就多能源系统的脆弱性与恢复力展开研究,探讨了韧性电网领域的研究需求。文献[6]考虑微电网多次中断的情况,识别脆弱构件的方法确保电力和天然气基础设施的协调运行,解决了多能量载体微电网在不同封锁条件下脆弱性的问题。

文献[3-6]是针对IGES的弹性评估,但均对天然气网络侧作出天然气网络不会受到极端灾害事件扰动的假设。大多数针对极端灾害事件的研究是通过某一具体灾害现状的具体数据进行IGES弹性分析,如文献[7]的极端事件为2018年的超强台风“山竹”,文献[8]为“桑美”台风和汶川地震作为极端事件,得到的系统弹性评估结论均不具备一般性。

针对上述问题,本文提出一种在极端灾害事件扰动中,考虑天然气网络特性故障特点的IGES弹性评估方法。首先,基于可靠性分析的一般故障随机模型,通过增加模型概率以及危害性,将故障节点进行故障传播处理,模拟极端灾害事件带来的扰动,并通过参数生成极端灾害事件故障场景。然后,建立IGES的电力网络侧、天然气网络侧以及耦合装置之间的时变模型,同时考虑在极端事件中提供恢复策略的两种能源网络的储能装置。最后,建立IGES弹性评估指标,并通过蒙特卡罗算法模拟验证了极端事件场景下IGES弹性评估策略的有效性。

1 极端灾害下IGES建模

在极端灾害下的IGES中,其配电网元件及线路故障概率同传统可靠性评估背景下的配电网线路相比,故障率大幅提升,且发生过程迅速,故障面积大,系统损失严重。极端灾害下IGES的建模包括故障传播建模、元件故障建模、储能装置建模以及约束条件4部分。

1.1 故障传播模型

极端灾害扰动除了损失严重,还有故障面积大的特点。为模拟该特点,假设元件损坏后,会引起周围线路连接元件的损坏,同时将故障按照一定概率进行传播,形成级联效应。依照文献[9]的故障传播策略,采用节点度Un、节点介数Kn、介数权重节点度Bn3 个指标作为传播介数,取前k次计算的平均值作为节点故障传播弹性指标。计算上述3个指标得到故障传播的系统参数表达式如下:

(1) 节点度[9]

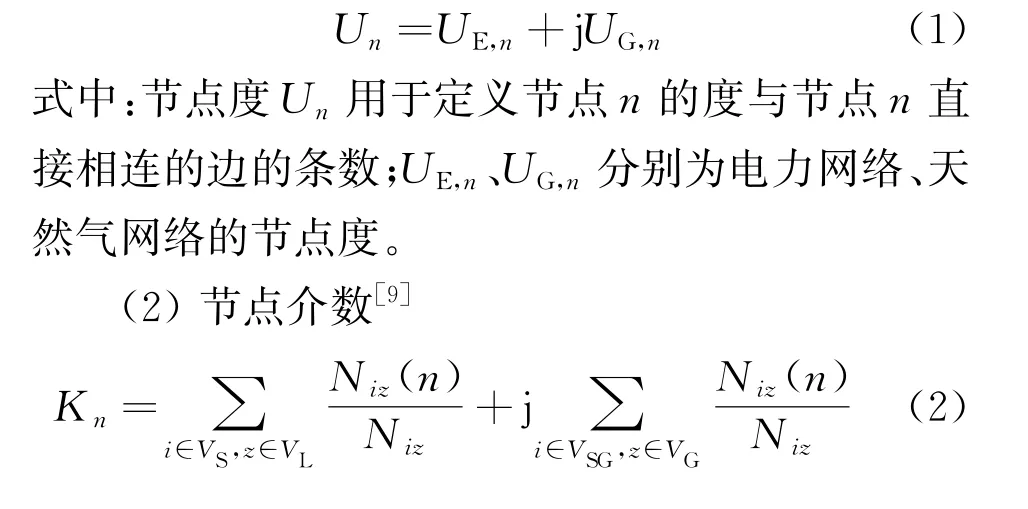
式中:i为等值电源节点编号;z为等值负荷节点编号;VS、VL分别为解耦后等值电源节点、电力负荷节点集合;VSG、VG分别为天然气节点、网络节点集合;Niz为等值电源节点i到等值负荷节点z的最短路径数目;Niz(n)为Niz中经过节点n的数量。

(3) 介数权重节点度[9]。由式(1)、式(2)可知,节点度与节点介数不能反馈边界节点的重要性,因此引入节点n的介数权重节点度

式中:VE为电力网络节点集合;Vm为节点n与节点p建立连接后的数据集;KL(n,p)为线路(n,p)中所包含的线路节点介数;KE,p、KG,p分别为电力网络、天然气网络节点p的线路节点介数。

1.2 元件随机故障模型

为描述极端灾害扰动的模型,建立负荷时变模型反馈负荷在极端环境中的扰动[10],负荷时变模型表达式为

式中:ϑi(t)为节点i在t时刻下的不确定性因子,即极端灾害下的负荷随机波动性;MP(t)、MQ(t)分别为负荷有功、无功功率的水平乘子,以描述负荷日变化特性;PLB,i、QLB,i分别为节点i上负荷的有功、无功功率的基准值;Pload,i,t、Qload,i,t分别为t时段节点i上负荷消耗的有功、无功功率;Li,t为t时段节点i上的负荷值;Δt为故障时段的各时间区间,非特殊说明,默认Δt=1。

上述电力网络中的扰动模型,针对节点之间拥有n条分支管路,可在天然气网络侧建立对应的流量方程时变模型为

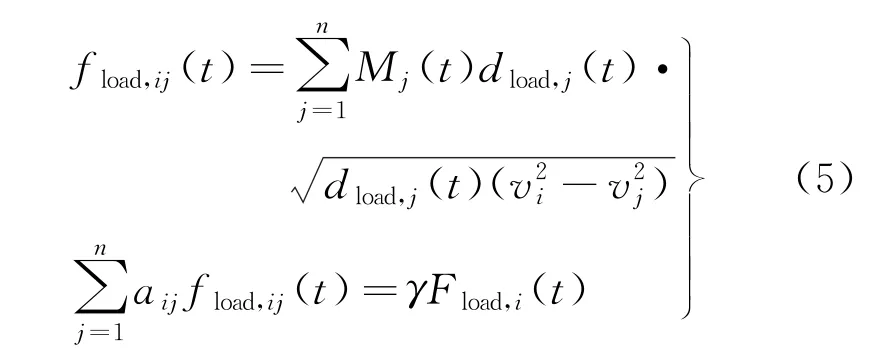
式中:Mj(t)为节点j管路常数;dload,j(t)为管路中天然气的流向,随着时间变化在[-1,1]两个数值中选取,而当极端灾害扰动发生时,则置0;fload,ij(t)为节点i到j的管道流量;vi为节点i位置的管道压力;aij为节点支管道对应的指标,表明管路分支j与节点i是否能够发生连接;Fload,i(t)为节点i中引进的外界能源,没有外来天然气源时,Fload,i(t)=0;γ为天然气源误差系数,一般在节点数少于20的天然气网络中设置为0.95。

1.3 储能装置模型

储能装置是极端灾害扰动系统时系统弹性评估的重要设备,一般在IGES中采用化学电池、储气罐两类作为储能设备,建立各类储能模型如下:

(1) 储电模型。参考文献[10]的储电模型,采用储能成本更低、储能寿命更长的磷酸铁锂电池组成储电系统,其模型表示为[11]

式中:hsoc(t)为t时刻储电系统的荷电状态;ηZ 为储电系统的自放电率;Pch,t-1、Pdch,t-1分别为t-1时刻储电系统的充放电功率;ηC、ηD 为充放电效率;USOC为储电单元的额定电压值;hsoc,max、hsoc,min分别为荷电状态的上、下限;Pch,max、Pdch,max为单位时段内最大充放电功率。

(2) 储气模型。储气罐用于分配天然气源的输出,作为备用容量通过IGES的燃气轮机以增加电能的输出。为便于计算,假设储气罐为理想模型,不考虑储气罐工作时进出气的压力变化,其模型[11]为

式中:Qa,t为t时刻储气罐a的储气总量;Qa,0为初始容量;Xin,a,t、Xout,a,t分别为储气罐a在t时刻的进气量与出气量;Xin,a,max、Xout,a,max分别为储气罐a的最大进气量和最大出气量;va,t、ζa,t为0～1的整数变量,分别为t时刻储气罐的进气或出气情况。

(3)IGES耦合装置。燃气轮机是IGES系统中重要的耦合元件,可将天然气供给到电力系统中,其能量转化满足

式中:PP2G为P2G装置耗用功率;t为设备工作时长;ηP2G、γE分别为该设备实际效率、电热转换性能参数;EP2G、HG、fP2G分别为该设备输出的能量大小、天然气燃烧值以及产生的燃气流量[12]。

1.4 IGES约束条件

IGES的约束关系包括两种能源系统的网络潮流关系约束,两种能源之间耦合装置的约束关系,以及涉及弹性评估时储能装置约束关系如下:

(1) 网络潮流关系约束。网络潮流关系约束包括等式约束和不等式约束[11]。同IGES相关的潮流约束主要集中于电、气两种能源网络的能流关系约束,电力一般由电压Ui,t、功率Pi,t两个指标作为潮流约束,天然气一般由压强pG、流量fG两种指标作为约束。

(2) 耦合装置及效率约束。耦合装置的约束主要由燃气轮机出力、P2G装置出力的约束,以及对不同能源转化的效率约束组成。约束表达式为

式中:PGT,i为节点燃气轮机的出力;PGT,i,min、PGT,i,max分别为燃气轮机出力的上、下限;PP2G,i为P2G装置的出力;PP2G,i,min、PP2G,i,max分别为P2G装置出力的上、下限;φ为耦合装置的转化效率;μi,t为单台耦合装置的理论转化极限值,一般燃气轮机约为0.6～0.8,P2G装置约为0.2～0.4。

(3) 储能装置约束。储能装置约束一般由储能装置的容量、单位时间的能流转换上下限以及能流转换速率决定。约束表达式为

2 IGES弹性评估

通过式(4)～式(19)以及目标函数构建针对极端灾害事件下的IGES扰动模型。依照文献[10]的恢复力指标建立目标函数和求解模型,整个弹性指标分析流程如图1所示。

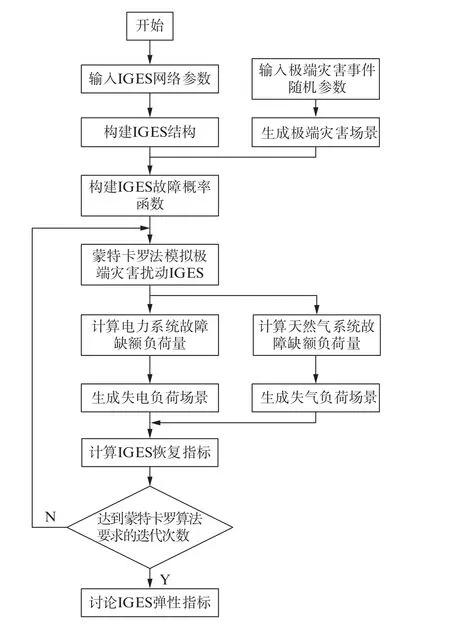
图1 IGES弹性指标分析流程

2.1 目标函数

在极端灾害的扰动过程中,为确保两种能源网络的正常供给,应保证系统内负荷恢复总量最大,则极端灾害扰动下IGES的目标函数为

式中:ωi为节点负荷i的受损比例;φi,t为可控负荷i的供电比例;CL为可控负荷的集合,i∈CL⊂M,M为孤岛m中总负荷节点合集;μj,t为不可控负荷节点j在t时段的带电状态;Li,t、Lj,t分别为负荷节点i、j在时段t内负荷量。

2.2 评估指标

弹性评估的侧重点是针对发生概率较低但影响严重的极端事件,一般通过确定性假设对弹性指标展开研究。因此,IGES弹性评估指标可描述为[13]

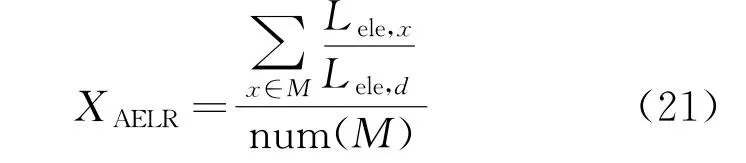
式中:Lele,x、Lgas,x分别为极端事件x下,IGES耦合运行时损失的电力负荷量与天然气负荷量;Lele,d、Lgas,d分别为IGES中电力网络与天然气网络的负荷总量;M为极端事件迭代合集;num(M)为集合M的数量,通常取值为20。

3 算例分析

3.1 仿真模型

仿真环境基于Matlab/Simulink的Matpower软件包,仿真算例以IEEE-39的电力网络和比利时20节点的天然气网络构成IGES,作为极端灾害扰动对象[14],其拓扑结构及节点编号如图2所示。

图2 天然气系统构成的电-气综合能源系统

基于以上极端灾害数据得到扰动后的IGES模型,通过式(21)、式(22)的恢复力指标结合IGES建立场景,得出IGES的弹性评估数据和仿真结果,并进一步分析IGES 在极端灾害扰动中的影响[15]。

3.2 仿真结果分析

极端灾害扰动后,IGES发生大面积系统故障,将网络拓扑结构的对应关系还原到元件-线路关联矩阵中。若元件损坏,则将该元件及其连接的所有线路都视作100%程度的损坏。对关联矩阵,若线路损坏,则仅视作该线路两个元件的连接关系为100%程度的损坏,反应到关联矩阵就是元件与线路的关联关系置0[16]。建立仿真算例的极端灾害扰动场景如图3、图4所示。

图3 IGES的电力系统中的弹性场景

图4 IGES的天然气系统中的弹性场景

图5、图6 所示为故障传播后,极端灾害对IGES两种网络系统的扰动场景。其中,“×”标记部分为扰动后的故障节点与线路,黑色标记部分为扰动的故障传播源。整个扰动传播的结果以负荷为中心或者以电网出力节点、天然气网络出力节点为中心,呈现向外发散的故障趋势。

图5 极端灾害在IGES电力系统中的扰动场景

图6 极端灾害在IGES天然气系统中的扰动场景

图7、图8为某次极端灾害扰动下,IGES电力、天然气节点负荷出力数据图。由图可知,相较于天然气网络,负荷节点更多、耦合时间更快的电力网络的节点扰动程度更大,而天然气同样也存在负荷节点受扰动的情况,基于蒙特卡罗算法多次迭代后,极端灾害下IGES的扰动指标见表1、表2。

图7 极端灾害下电力节点负荷出力

图8 极端灾害下天然气节点负荷出力

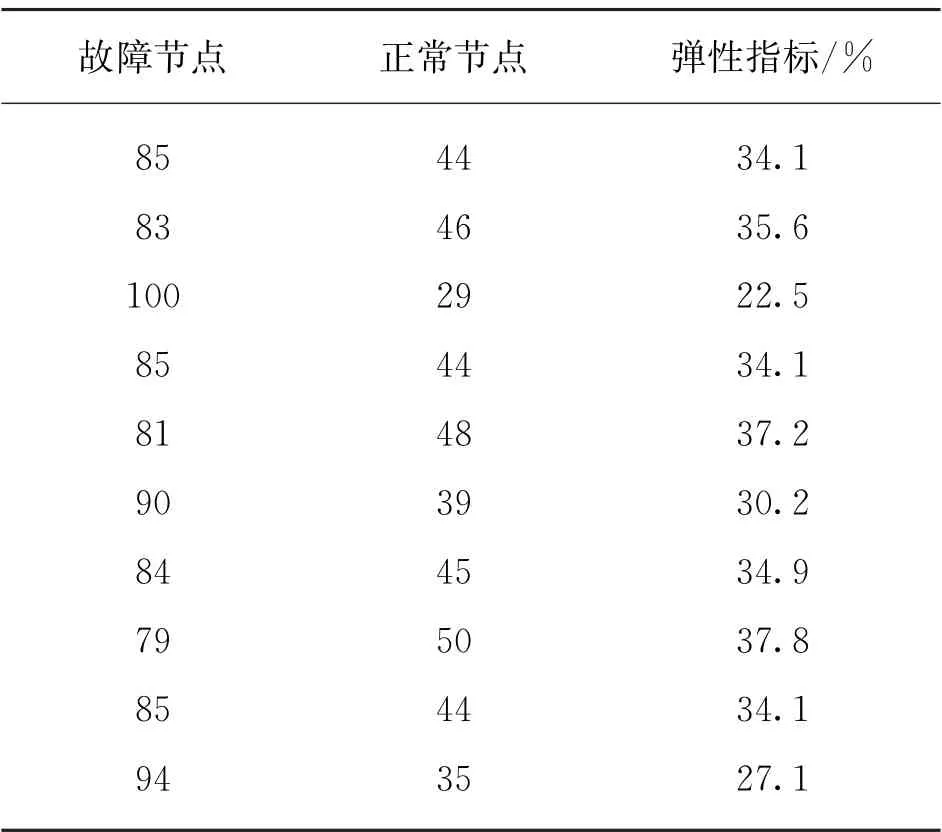
表1 极端灾害扰动电力网络弹性指标

(续表1)

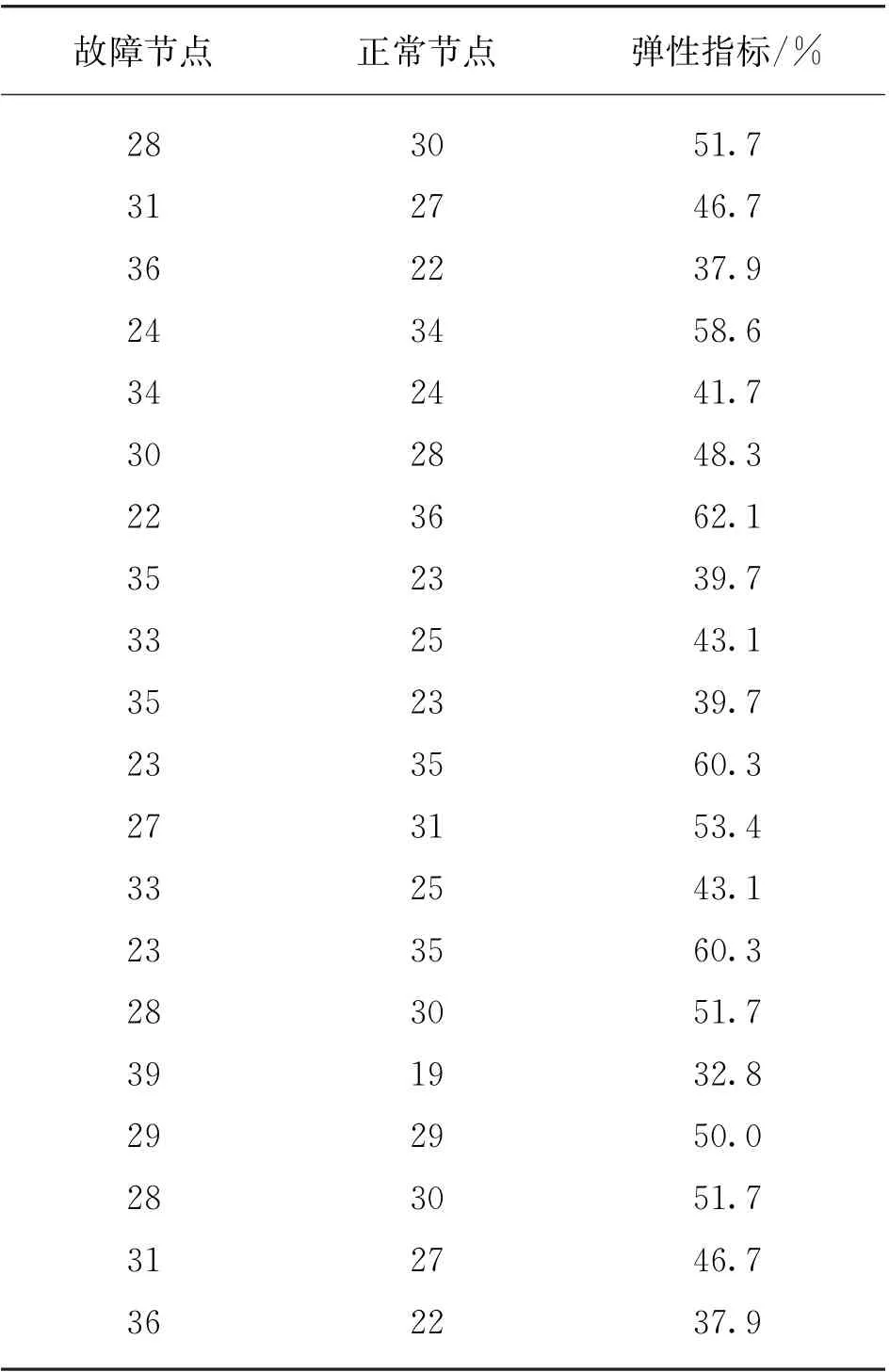
表2 极端灾害扰动天然气网络弹性指标

由表1、表2可知,在同样场景的极端灾害扰动中,天然气网络侧的弹性指标(18.6%～38.8%)要明显好于电力网络侧的弹性指标(34.5%～62.1%),但天然气网络侧也会因极端灾害扰动使得系统负荷波动,故不能对IGES的天然气网络侧作理想化处理,默认不会受到极端灾害扰动。

4 结 论

本文研究了IGES在极端灾害扰动下的弹性评估。先通过故障传播机制得到极端灾害扰动模型,然后提出考虑天然气的IGES随机故障模型。本文的弹性评估策略为极端灾害扰动下考虑天然气网络的IGES弹性评估建立了评估步骤,同时也为IGES弹性评估带来一定现实意义上的理论指导。本文未考虑极端灾害扰动的经济因素,未来将进一步研究在经济成本优化调度下有关IGES在极端灾害场景的建模方法。