基于LSGAN 和GA-ELM 的风电功率短期预测

赵睿智, 丁云飞

(1.国网上海市电力公司长兴供电公司, 上海 201913;2.上海电机学院 电气学院, 上海 201306)

风电功率的短期预测多采用风电场的数值天气数据(Numerical Weather Prediction,NWP)。NWP数据具有一定的规律性和差异性,相似天气和极端天气的NWP数据差异显著,因此对NWP数据作聚类分析是十分必要的。目前,基于聚类分析的风电功率预测研究已卓有成效,文献[1-3]采用聚类算法对功率数据进行聚类分析预测,均取得良好的效果。

尽管NWP的聚类分析已在风电预测中产生良好的效果,但其未考虑聚类后不同类别的数据是否平衡,即正常天气NWP的数量远远大于极端天气的数量的情况。若将非平衡数据代入模型中训练,则容易导致多数类预测效果优于少数类。针对非平衡数据集问题,文献[4]在数据过采样处理前,对不平衡数据进行聚类划分,缓解了过采样技术难以处理类内不平衡数据的缺陷。文献[5]首先获取非平衡数据的概率密度,再通过概率增强生成少数类,从而达到数据平衡。文献[6]通过引入修正因子抑制多数类样本的权重,扩大少数类样本的权重,进而达到分类的平衡性。针对非平衡问题,前期研究的重点在于诊断模型的权重分配,该类模型的可适应性因数据的变化而改变。

生成对抗网络[7](Generative Adversarial Network,GAN)作为少数类样本的生成方法为样本不平衡难题提供了新的解决思路。目前,衍生出许多优化的GAN 算法,如深度卷积生成对抗网络[8](Deep Convolutional GAN,DCGAN)、条件生成对抗网络[9](Conditional GAN,CGAN)、最小二乘生成对抗网络(Least Squares GAN,LSGAN)等。这几类算法已用于多种领域并取得良好的效果。胡若晖等[10]采用DCGAN扩充少量的轴承振动信号,实现了少量样本情况下轴承诊断的新思路。CHENG等[11]通过DCGAN 算法生成频谱数据,实现了小样本条件下的通信行为识别。张文强等[12]利用CGAN 算法生成特定条件下光伏的功率序列,缩小了特定天气下光伏不确定出力的范围。ZHOU 等[13]采用CGAN 来实现书法汉字的生成,有效解决了汉字笔画遗漏的情况。

本文受对抗博弈思想的启发,采用LSGAN 算法生成风电功率少数类的NWP数据,用以改善GAN方法训练的不稳定性,达到不同类样本数据的平衡。然后,采用基于遗传算法的极限学习机(Genetic Algorithm Extreme Learning Machine,GAELM)模型[14]进行预测,用以提高预测模型的精度。

1 基本理论

1.1 模糊C均值算法

模糊C 均值(Fuzzy C-Means,FCM)算法采用隶属度描述数据归为每个类别的隶属程度。该算法的基本思想为:将欲聚类的数据集X=[x1,x2,…,xN]划分为c类,其中,x1,x2,…,xN为欲聚类的样本数据,N为样本数量,2≤c≤N,假设聚类中心V=[v1,v2,…,vc]T。

目标函数J的计算公式为

式中,λ为拉格朗日因子。

1.2 生成式对抗网络算法

GAN是一种无监督的神经网络,由生成器(Generator,G)和判别器(Discriminator,D)构成,其思想源于零和博弈思想[15],生成器G学习真实样本的特征分布,将随机噪声优化为逼真的虚拟样本;判别器D是二分类器,甄别虚拟样本与真实样本。具体框架如图1所示。

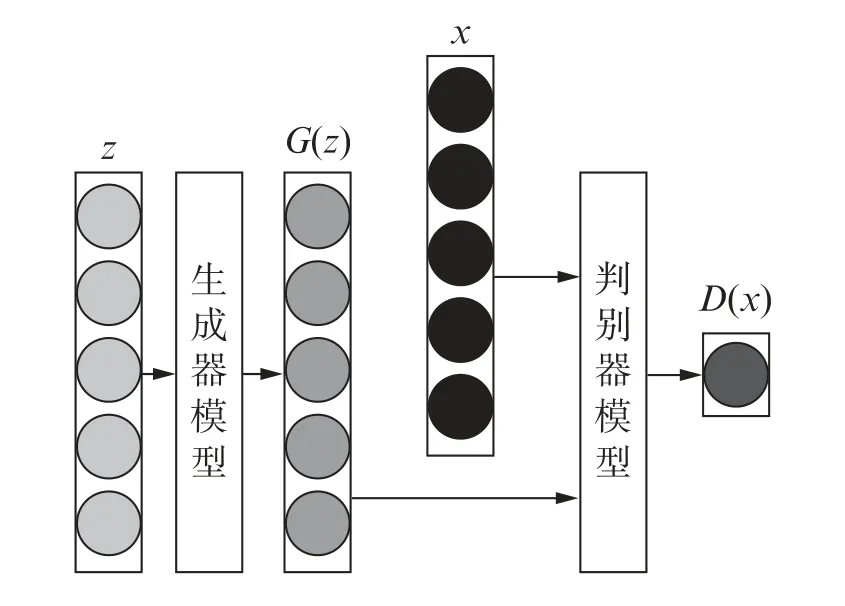
图1 GAN基本结构

假设随机噪声为z(z服从高斯分布Pz),真实样本为x(x服从实际分布Pr),生成器输出为G(z);判别器进行甄别,得到D(x)和D(G(z))。G的目标是使G(z)的分布趋近真实样本x的分布,即Pg逼近Pr,而D的目标是区分G(z)和x。经过多次迭代,使得Pg无限逼近Pr。

G和D的损失函数为

式中:E(·)为数学期望;G(z)为G生成的样本数据;D(·)为判别器的输出结果。

1.3 LSGAN算法

GAN算法的损失函数存在的问题是JS散度不能拉近真实数据和生成数据之间的距离。被判别器D鉴别为真实样本的生成样本,样本离决策边界很远,也无法被生成器G优化,这导致G生成的样本数据质量不高。最小二乘损失函数的优点是将离决策边界较远的生成数据拉近到决策边界,从而使生成数据被G优化。LSGAN 算法采用最小二乘损失函数代替了GAN 的损失函数,降低了GAN算法稳定性低和生成数据质量差的程度。

LSGAN的目标函数为

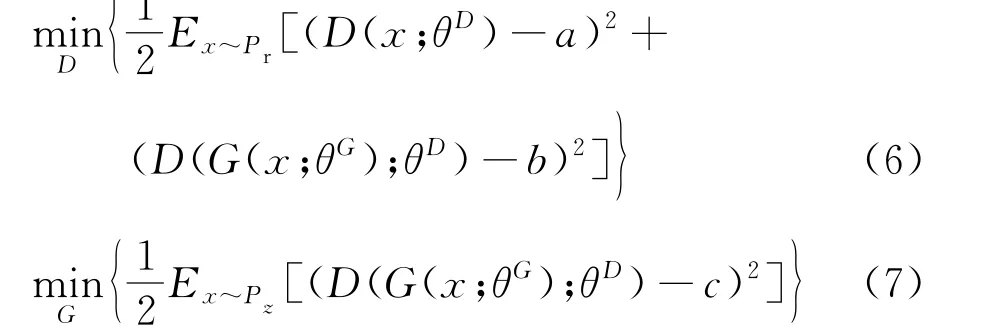
式中:D(x;θD)为判别器;G(x;θG)为生成器;a为真实样本数据标签;b为生成样本数据标签;c为生成器参数;a=c=1,b=0。

1.4 GA-ELM 算法

ELM 的输入权值和阈值是随机确定的,因此ELM 模型训练的效果和时间具有随机性[16]。本文采用GA 方法对ELM 模型的输入参数进行寻优,具体步骤如下:

(1) 设置初始参数,产生初始种群、迭代次数、初始权值和隐层阈值;

(2) 设置适应度函数,通过GA 模型的不断选择、交叉和变异,经过多次迭代,获取最优的权值w与阈值b,将迭代后的均方根误差S作为GA 适应度函数,公式为

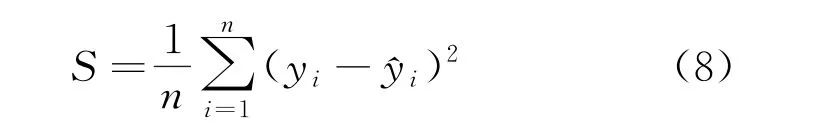
式中:n为测试样本数;yi为预测值;^yi为实际值。

(3) 将优化后的权值和阈值代入ELM 网络,建立GA-ELM 模型。

2 基于LSGAN和GA-ELM 的预测模型

2.1 训练样本聚类

采用FCM 算法将NWP数据进行聚类分析,得到聚类类别数c和隶属度矩阵,根据隶属度值判断样本所属类别。以聚类有效性评价指标为准则,确定NWP数据样本聚类的最佳数量。假设聚类数量为c时V(U,V,c)最小,此时NWP数据已被分为c种典型天气类型,确定类别中心cj和各典型天气类型的样本数据。

聚类有效性的评价指标如下:

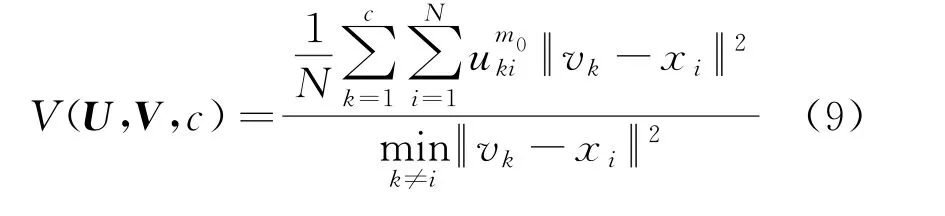
式中:U为隶属度矩阵;V为聚类中心;c为聚类数量;xi为第i个点的位置;vk为第k个聚类中心的位置;分子部分表示各聚类中心的紧凑性,分子越小表明各类内部越紧凑;分母部分表示各聚类之间的独立性,每个类之间的距离越大,则表明各类之间的独立性越强,聚类中心越疏远。

因此V(U,V,c)越小,则表明各聚类内部越紧凑,各聚类之间越独立,进而表明聚类分析结果越合理。

2.2 LSGAN数据生成

由FCM 算法获得c类NWP数据[D1,D2,…,Dc],比较各类数据的数量,选出最大数量的数据Di(i∈[1,c]),分别将其他数据Dj(j∈1,2,…,c,j≠i)作为真实样本数据集代入LSGAN 模型中生成新的数据集D′j,使D′j的样本数量等于Di的样本数量。因此,数据集[D1,D2,…,Dc]经过LSGAN模型转变为数据集[D′1,D′2,…,D′i,…,D′c],各类样本数据集由非平衡状态调整为平衡状态。

2.3 建立模型

首先,将风电功率NWP数据进行预处理,再采用FCM 算法对NWP数据进行聚类,获得c个典型天气类型。判别不同天气类型的数据集是否平衡,若数据集非平衡,则将数据集代入LSGAN数据生成模块生成该天气类型的新样本,进而达到数据集平衡。将平衡后的数据集代入GA-ELM 模型进行训练,建立GA-ELM 预测模型。将测试数据代入模型中获得预测结果,具体流程如图2所示。

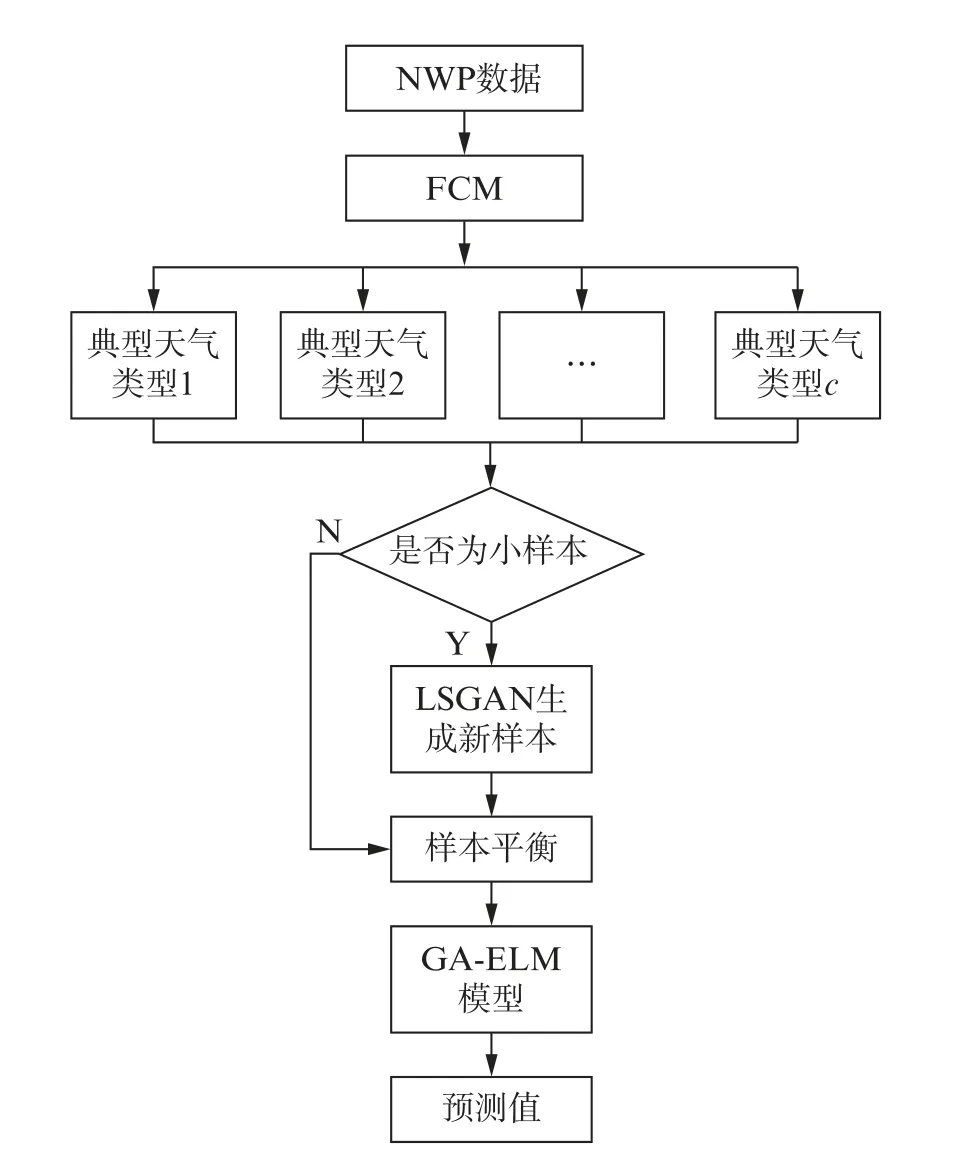
图2 基于LSGAN和GA-ELM 的风电功率短期预测流程

3 评价指标

为了验证模型的预测效果,本文分别以绝对平均误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、均方根误差(Root Mean Square Error,RMSE)作为评价指标。其公式为

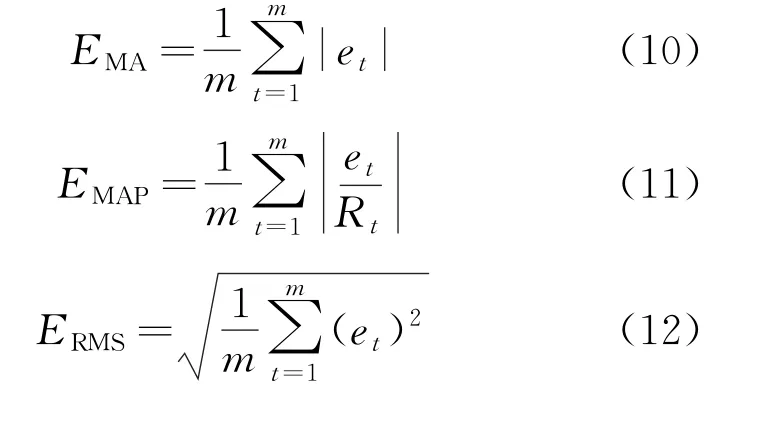
式中:et=Rt-Yt为预测绝对误差值;Rt为第t个风电功率实测值;Yt为第t个风电功率预测值;m为预测时间点数。

4 仿真实验

本文以上海某14 MW 风电场2017年5月份的NWP数据为例。该NWP数据包括风速、风向、温度、气压、空气密度5项特征,时间间隔为1 h。分别将第1～28 d的NWP数据共672组数据作为训练集,将第29～31 d共72组数据作为测试集。该风电场5月份的风电功率时序图如图3所示。

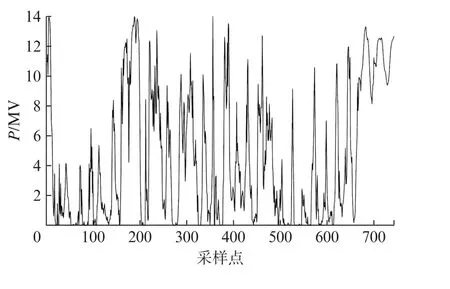
图3 上海某14 MW 风电场5月份功率时序数据

4.1 NWP数据的聚类分析

采用FCM算法将风电场的NWP数据进行聚类分析,计算不同聚类数目的聚类有效性V(U,V,c),进而确定最佳聚类的数量。NWP数据聚类分析中不同聚类数目的有效性函数值见表1。

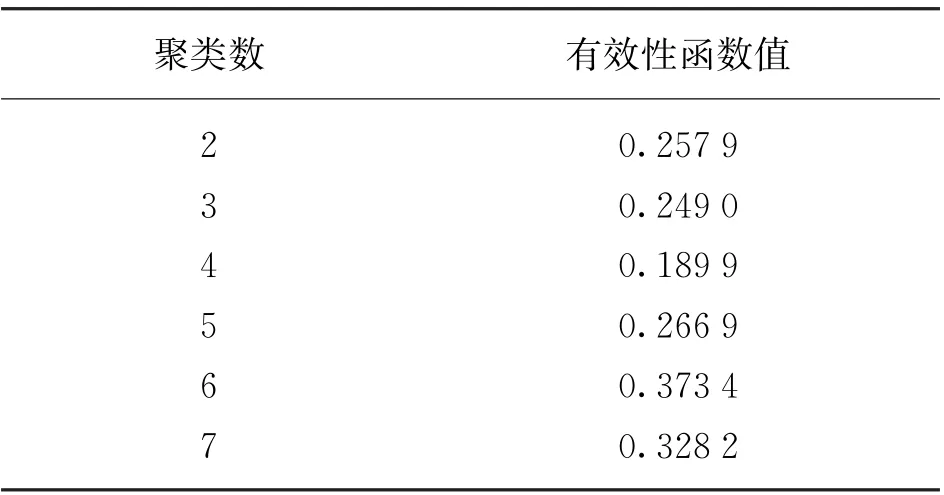
表1 FCM 的聚类数和有效性函数值

由表可知,FCM 方法在聚类数为4时聚类有效性取最小值,这说明该NWP数据最佳可分为4种典型天气类型。

将4类典型天气类型分别记为聚类集D1、D2、D3、D4。每个聚类集中的样本个数见表2。

表2 各聚类集中样本个数

4.2 LSGAN平衡样本集

本文使用的LSGAN 和GAN 模型中,生成器G中隐含层的激活函数采用Relu函数,输出层则采用tanh函数。判别器D中隐含层的激活函数选用ELU 函数,输出层无激活函数。

将聚类集D1、D3、D4分别按照D2的样本数量进行LSGAN的样本生成。以D1为例,LSGAN和GAN模型中的G和D的损失函数曲线,如图4、图5所示。由图4可见,LSGAN模型中G损失函数会急剧降低,并在达到一定迭代次数后趋于稳定,曲线变化小、收敛快。这表明LSGAN中生成器在整个训练过程中稳定性好,其损失函数收敛迅速。与此对比,GAN模型中G损失函数在迭代过程中波形变化大,收敛过程中产生多次发散,这表明GAN模型中生成器在整个训练过程中稳定性较差。由图5可见,LSGAN模型中D损失函数会急剧降低,达到一定迭代次数后趋于稳定,这表明LSGAN 中判别器在训练过程中稳定性好且收敛快。GAN 模型中D损失函数在迭代过程中曲线变化大,无法迅速收敛。

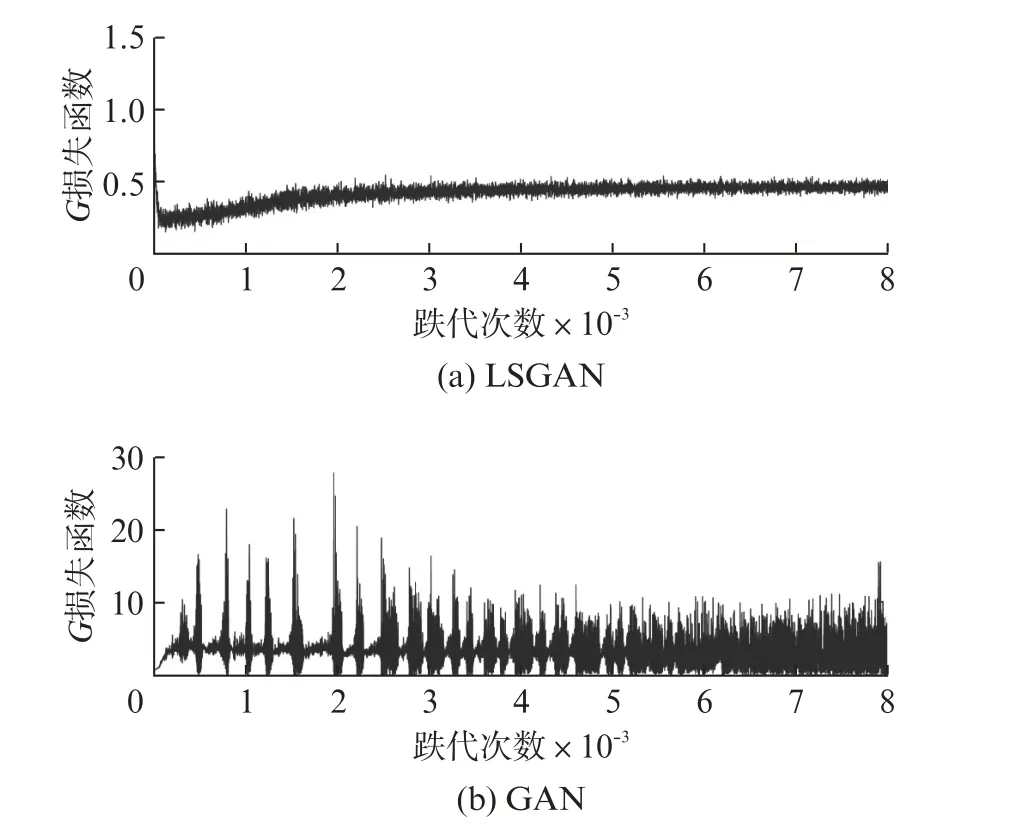
图4 LSGAN和GAN中生成器G 损失函数的对比结果

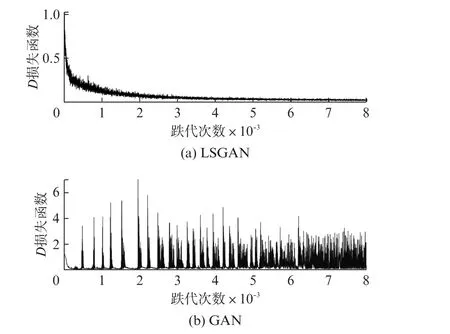
图5 LSGAN和GAN中判别器D 损失函数的对比结果

迭代完成后,LSGAN 和GAN 模型中判别器D对生成样本的判定结果,如图6所示。可知,LSGAN中判别器的判别概率在[0.4,0.7]上下波动,判别概率在0.5～0.6内居多,表明LSGAN 的判别器实现了纳什平衡。由于GAN 中判别器的损失函数未收敛,导致GAN 中判别器的判别概率上下波动大,判别概率多为0或1。

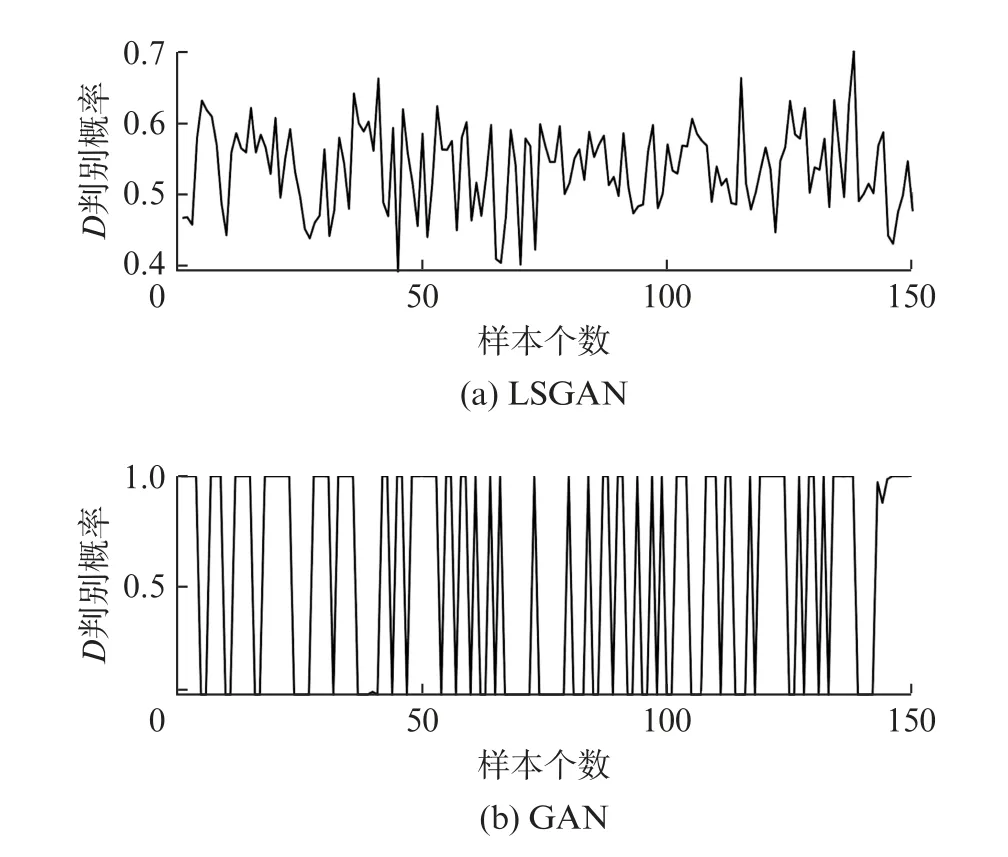
图6 LSGAN和GAN中判别器对噪声生成样本的判别概率

4.3 预测结果分析

经过LSGAN 生成后的NWP数据集为[D′1,D′2,D′3,D′4],各类之间均具有平衡性。本文针对该数据集进行GA-ELM 预测,模型参数见表3。

表3 GA-ELM 的网络参数设置

风功率预测结果如图7所示。LSGAN-GAELM 模型预测曲线拟合程度优于GAN-GA-ELM模型,这表明LSGAN方法生成的样本数据更贴近于真实数据。

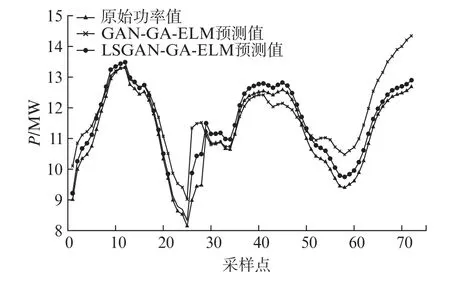
图7 风电场5月份功率预测曲线

各种方法的预测评价指标见表4,GA-ELM 模型的MAE值和RMSE值明显低于ELM 模型,这说明GA算法优化ELM 算法的输入权值和阈值可提高预测的精度。GAN-GA-ELM 模型和LSGANGA-ELM 模 型 的MAE、RMSE、MAPE 值 均 比GA-ELM 模型小。这表明对风电NWP数据进行聚类分析,并采用GAN 算法生成少类样本数据,达到各类样本的平衡,使得模型训练更加完善,可提高预测的精度。LSGAN-GA-ELM 模型的MAE、RMSE、MAPE值分别比GAN-GA-ELM 模型降低了0.374 3 MW、0.537 5 MW、3.63%,这说明最小二乘损失函数使模型波动小,也更稳定,样本生成质量高,进而预测模型效果更好。为了验证本文算法的广泛性,本实验同时采用了9月份、12月份的NWP数据,分别对比了ELM、GA-ELM、GAN-GA-ELM、LSGAN-GA-ELM 模型的预测效果。对比结果显示,LSGAN-GA-ELM 模型在风电功率预测中精度更高,稳定性更好。

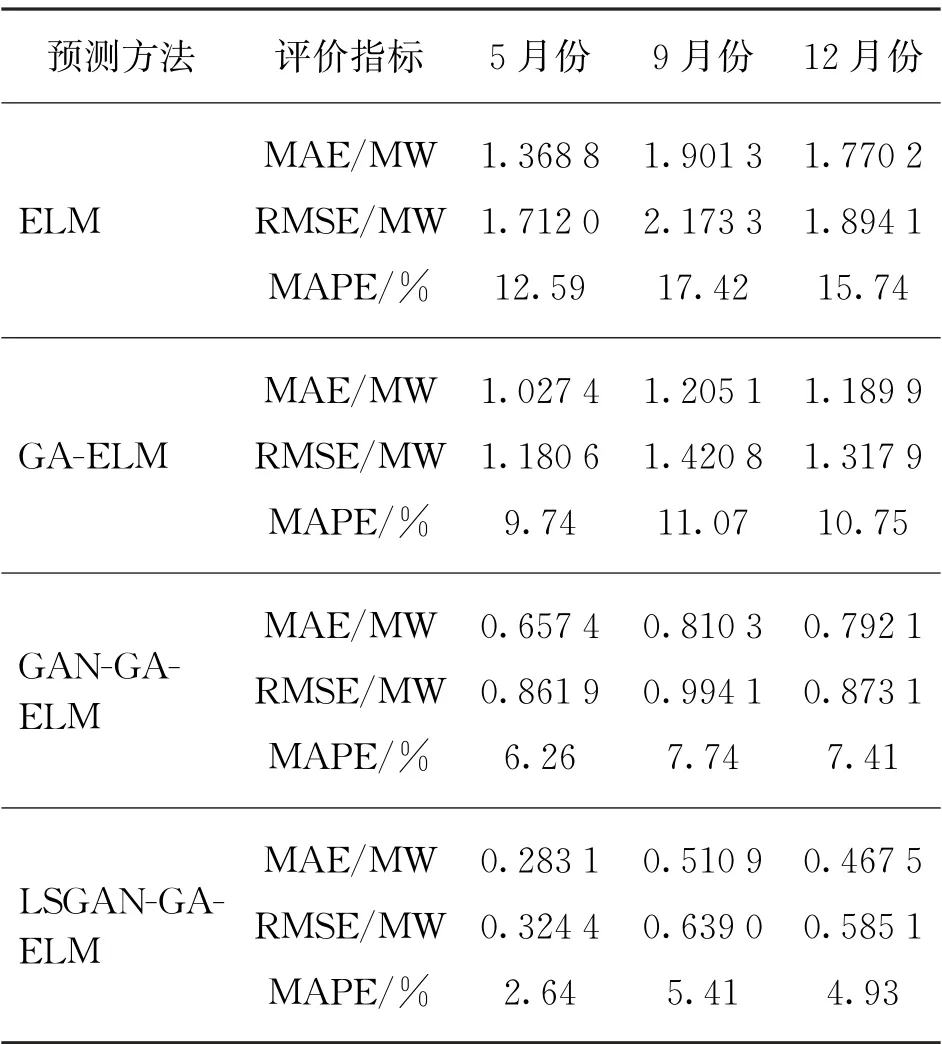
表4 风电功率预测的评价指标

5 结 语

本文提出了基于LSGAN 和GA-ELM 的风电功率短期预测方法。针对NWP数据的规律性和差异性,将NWP数据进行聚类分析,再采用LSGAN方法生成少数类样本的数据,从而达到各类样本的平衡,再通过GA-ELM 模型对平衡样本进行训练和预测。

分析了LSGAN 和GAN 方法损失函数之间的变化趋势,对比了2种方法在生成数据中产生的效果,进而得出LSGAN 方法在处理该风电场NWP数据时更稳定且收敛更快。通过对比各类方法的预测效果,得出本文方法预测效果更优。本文方法是GAN 相关理论在风电功率预测领域的应用和延伸,为风电功率短期预测和处理非平衡问题提供了有效途径。