基于响应面法的单相感应电动机多目标分析优化

殷世雄, 王爱元,2, 姚晓东,2, 王成敏, 李吉程

(1.上海电动机学院 电气学院,上海 201306;2.佛山市高明区明戈新型电机电控研究院,广东 佛山 528500)

感应电动机广泛应用于家用电器和轻型工业设备,如洗衣机、冰箱、空调、风机和水泵等,消耗着大量电能。感应电动机能效水平的提高,对节约电能有十分重要的意义。

如果要获得显著的节能效果,对感应电动机的效率和功率因数优化显得尤为重要。文献[1-3]分析了不同转子槽型对感应电动机运行性能的影响,得出改进转子槽型及转子槽参数可以提升电动机的效率。文献[4-6]采用各种算法对感应电动机进行了多目标优化设计,通过改变定转子的尺寸及槽型,提高了电动机的运行性能。文献[7]利用有限元仿真及田口正交表对感应电动机定子槽进行了优化设计,结果表明电动机的功率因数和效率都得到了改善。文献[8-10]利用响应面法对电动机进行了优化设计。在其他方面近年也有相应的研究,如调速控制[11-12]、谐波分析[13-15]等。

以上研究对单相感应电动机的分析较少,本文以1台600 W 单相感应电动机为研究对象,通过单因素仿真分析得出运行电容值C、转子槽高度hr12、转子槽宽度br2的初步优选值。由于电动机的很多参数都是非线性函数,所以采用正交实验表与响应面法相结合的方法,得到了电动机效率和功率因数为目标的二次多项式回归模型。对优化模型进行求解,获得最优变量组合,并进行进一步电磁场有限元计算。

1 电动机主要参数

单相感应电动机的定子绕组由主绕组和副绕组组成,且主绕组和副绕组的轴线在空间上和时间上都有90°相位差,以便产生起动力矩。

以YLB50-12型单相感应电动机为例,其主要参数如表1所示。利用响应面法对单相感应电动机的相关参数进行优化后,进行电磁场有限元计算。

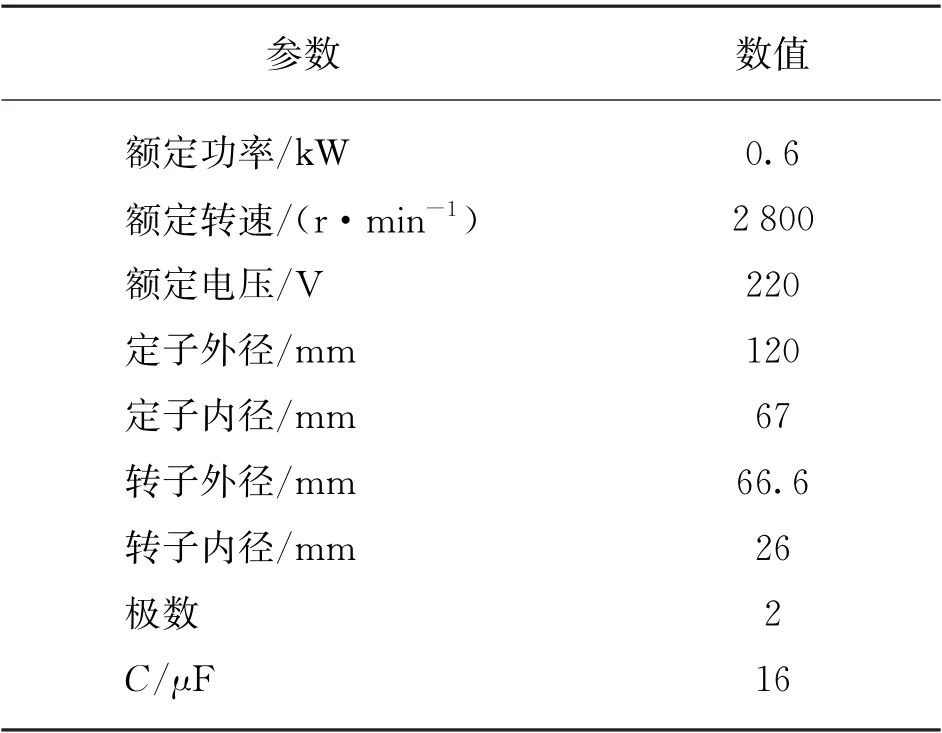
表1 电动机主要参数

2 多变量多目标的优化设计

2.1 单因素仿真分析

对于单相感应电动机来说,一旦调整运行电容,电动机的效率、功率因数等就会受到很大影响。因此,选择合适的运行电容,使气隙磁场近似为圆形,电动机的运行性能便能得到优化。通过仿真计算,得到不同C时电动机的效率及功率因数,如图1所示。

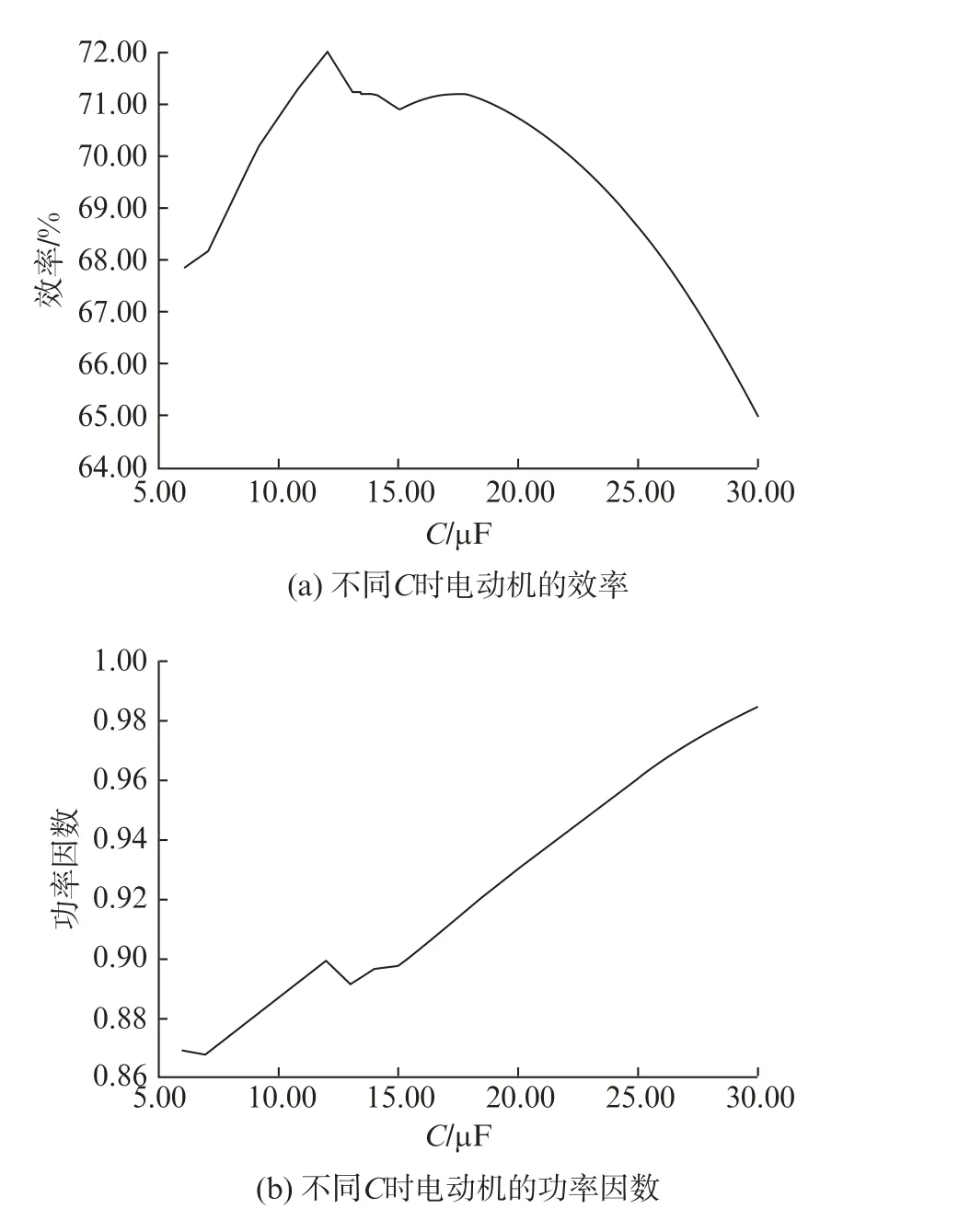
图1 不同C 时电动机的效率及功率因数

由图1可见,效率随C的增大大致呈现先增大后减小的趋势,而功率因数随C的增大大致呈现持续增大的趋势。

转子槽型和槽尺寸的变化,对电动机的运行性能也会有较大的影响,包括效率、功率因数、损耗等。图2和表2分别为单相感应电动机的转子槽型和尺寸。其中,槽高hr12及槽宽br2对电动机效率及功率因数的影响比较大。

图2 电动机的转子槽型

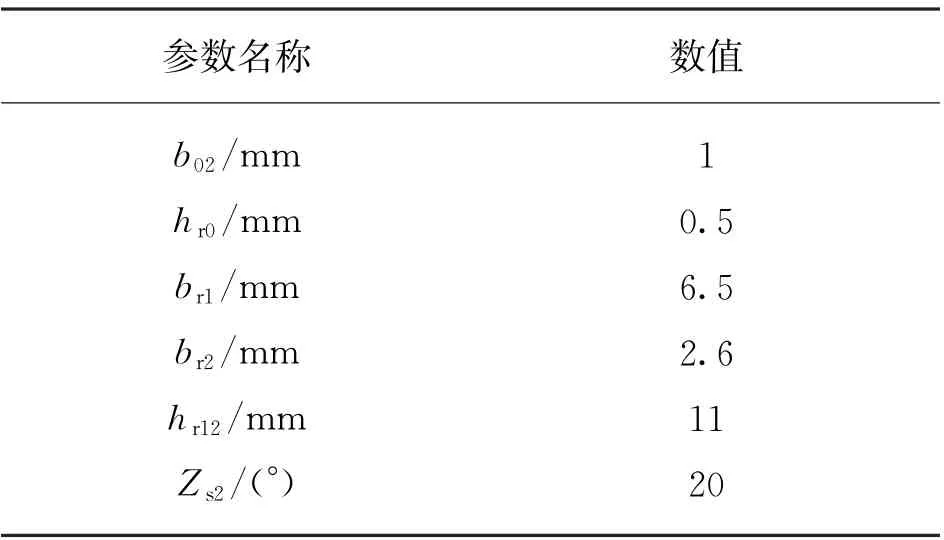
表2 转子槽尺寸参数

通过电磁场仿真计算,得到hr12、br2这2个参数对电动机效率及功率因数的影响,分别如图3、图4所示。

由图3可见,效率及功率因数随hr12的增大而大致呈现先略微增大后减小的趋势。

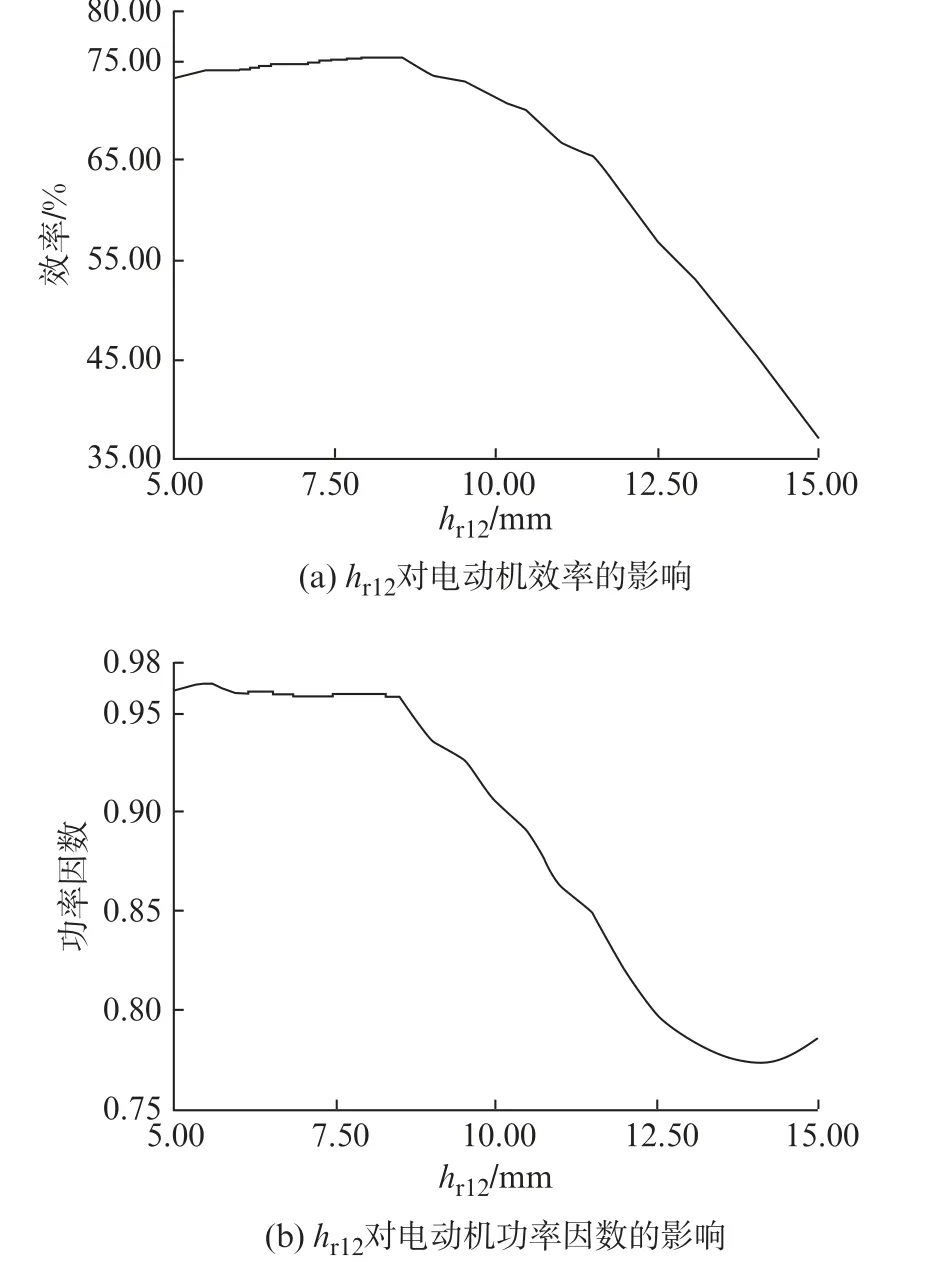
图3 h r12 对电动机效率及功率因数的影响

由图4可见,效率及功率因数在br2约为1.4 mm时达到最大值,随后减小,在br2约为2.3 mm 时呈现上下波动的趋势。

图4 b r2 对电动机效率及功率因数的影响

经过多次单因素仿真分析,对C、hr12和br2进行了参数的初步优选,大致确定了各项因素对效率及功率因数的优化区间。其中,C为8～17μF,hr12为7.5～9 mm,br2为1.2～2.7 mm。

电动机的优化设计是一个非常复杂的过程,多个设计变量和多个优化目标之间相互影响。为了得到比较好的变量组合,需要进行大量的计算。在考虑多个设计变量相互影响的前提下,采用正交实验可以有效减少计算量。

2.2 正交旋转多因素仿真实验

根据单因素仿真计算结果,选出合适的变量优化区间。每个变量在优化区间内均匀选取4个值作为水平等级,设计多因素正交旋转实验。选取水平等级及优化变量的变化区间如表3所示。

表3 水平等级及优化变量

利用Design-Expert软件,根据上述4个水平等级及优化变量建立16次实验,通过电磁场有限元仿真计算得到所需的数据。以C、hr12及br2为自变量(x1,x2,x3),效率及功率因数为优化评价指标(y1,y2),电磁计算结果如表4所示。其中,组号为1的实验为原点实验。

表4 正交实验结果

根据表4的实验数据,通过Design-Expert软件进行方差分析,得到效率及功率因数的二次多项式回归模型为

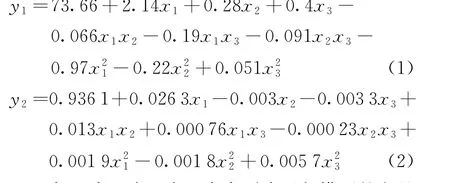
表5、表6为2个二次多项式回归模型的方差分析结果。模型的P值及其他数据均由软件计算得出,P值越小,代表此回归模型越有效,模型可用。效率及功率因数的P均小于0.000 1,证明模型有效且非常显著。由C、hr12及br2的P可知,3个实验因素对电动机效率及功率因数都有极显著影响。实验因素对电动机效率的影响从大到小依次为运行电容、转子槽宽、转子槽高。实验因素对电动机功率因数的影响从大到小依次为运行电容、转子槽宽、转子槽高;且2个回归模型的P＜0.05,故回归模型中的3个回归项交互影响突出。由方差分析可得精密度和变异系数分别为24.5、25.38和0.37%、0.34%,且在方差分析中,当精密度＞4、变异系数＜10%时模型可用。因此,该电动机效率模型与电动机功率因数模型具有非常高的可靠性。

表5 效率的方差分析

表6 功率因数的方差分析

由二次多项式回归模型的分析结果,可得到效率和功率因数的响应曲面图。考虑到由方差分析得出的3个实验因素中,运行电容及转子槽宽度影响占比大,因此本文只给出以运行电容和转子槽宽为变量的交互效应响应曲面,如图5所示。

如图5(a)所示,C由17μF减小到8μF的过程中,br2越大,电动机效率越低。如图5(b)所示,br2由2.7 mm 减小到1.2 mm 的过程中,C越大,电动机功率因数的增幅就越大。基于交互效应分析可知,运行电容与转子槽宽度同时增大和减小时,对电动机的功率因数增加效果显著。

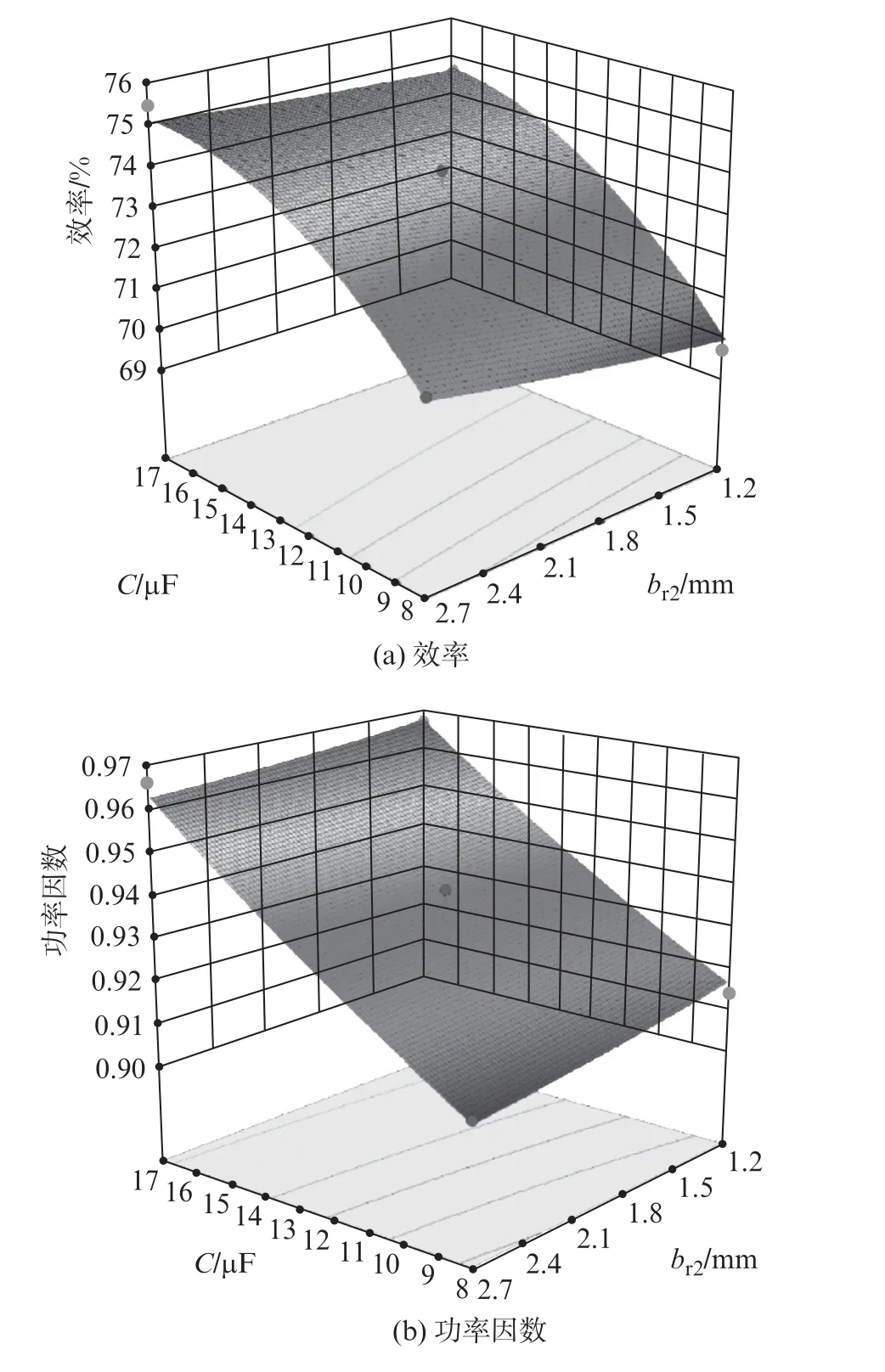
图5 交互效应响应曲面

3 参数优化与对比实验

利用电动机效率与功率因数的二次多项式回归模型,通过Design-Expert软件中的最优化功能,以最大化电动机效率与电动机功率因数为目标,求解回归模型得到的最优参数C为17μF、br2为1.2 mm、hr12为8.43 mm。

为验证优化参数是否可靠,在最优参数下,利用电磁场有限元仿真计算进行验证。考虑电动机的实际制造工艺,hr12取8.4 mm。回归模型与电磁计算的结果如表7所示。效率和功率因数的误差分别为0.90%与0.63%,指标基本一致。进一步与优化前的电磁场有限元计算性能进行对比,如表8所示。

表7 回归模型与电磁计算对比

表8 优化前后性能对比

4 结 语

针对单相感应电动机的效率和功率因数,利用单因素电磁场仿真计算进行C、br2、hr12的初步优选,在结果较好的区域确定优化区间。通过正交实验和Design-Expert软件得到二次多项式回归模型,求解出最优组合参数C为17μF、br2为1.2 mm、hr12为8.43 mm。在最优参数组合下,进行电磁场有限元计算的验算,与优化前的电磁场有限元计算相比,单相感应电动机效率提高了2.97%,功率因数提高了0.05。该结果表明,电动机的性能得到较大提高,且准确性较高,为单相感应电动机的优化设计提供了一定的依据。