DoS攻击下信息物理系统事件触发保性能控制

祝超群, 黄 鹏

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 兰州理工大学 甘肃省工业过程先进控制重点实验室, 甘肃 兰州 730050; 3. 兰州理工大学 电气与控制工程国家级实验教学示范中心, 甘肃 兰州 730050)

目前,综合了计算机、通信网络和物理空间的信息物理系统(cyber physical systems,CPS)在当下的网络化环境中得到了迅速发展,在生产制造、智能能源、智能家居和交通运输等行业的变革中有着举足轻重的作用[1-3].由于物理环境的限制,CPS中控制器、传感器和执行器等系统组件通过网络空间进行数据传输,势必会产生系统信息安全方面的问题.在开放的网络环境中,信息传输的准确性和时效性对物理环境的安全性影响深远[4].近年来,网络安全问题频出,2020年8月新西兰证券交易所受到网络攻击,袭击迫使交易所暂停其现金市场交易1 h,扰乱了其债务市场；2021年5月美国最大的成品油运输管道运营商遭黑客攻击,导致美国东南部地区的汽油供给大量中断.针对CPS的安全性问题,当前学者的研究主要集中在拒绝服务(denial of service,DoS)攻击、虚假数据注入(false data injection,FDI)攻击和重放(replay)攻击三个方面[5].其中,DoS攻击是一种试图使系统资源不可用的网络攻击模式,通常利用阻塞系统信道的方式来使系统性能下降甚至失稳,因其攻击形式易于实现,手段多样化而备受学者们的关注.

当前对于DoS攻击的研究主要是将其建模为数据包丢失的形式.Su等[6]将DoS攻击建立为一种周期性模型,并运用随机分析法证明了系统的随机稳定性.Yan等[7]建立了一种限制攻击持续时间的间歇性DoS攻击模型,研究了DoS攻击下CPS的故障估计问题.上述研究考虑的DoS攻击都是周期已知的,虽然此类DoS攻击便于实施,但周期性的攻击特点使其易于被检测.与周期DoS攻击不同,随机DoS攻击具有一定的不确定性,对控制系统造成的危害更大.Liu等[8]通过一个随机跳变系统表征了DoS攻击的随机性,并提出了一种模型依赖的弹性控制器来减轻DoS攻击的影响,该控制策略对微电网防御DoS攻击有很好的效果.Wang等[9]利用Bernoulli分布来描述DoS攻击的随机性,建立了一个具有随机干扰的系统模型,研究了随机DoS攻击下CPS的保性能控制问题.Bogdan等[10]针对遭受DoS攻击的离散时间网络化控制系统,采用伯努利随机过程描述传感器数据包丢失行为,在此基础上分析了系统的稳定性,但该文未考虑网络化系统中存在的其他各类通信约束.

随着CPS的快速发展,通信网络的负担也逐渐加重,数量庞大的数据包造成的网络拥塞使得系统控制性能大大降低.相对于传统的时间触发策略,事件触发通信在有限的网络资源环境下可减少不必要的数据包发送,有效地降低网络通信负担.近年来,基于事件触发的控制问题得到广泛关注[11-17].Peng等[11]提出了一种离散事件触发通信方案,是否传输量测信息由当前采样状态和当前采样状态与最近传输状态之间的误差决定.李炜等[12]在离散事件触发通讯机制下,针对一类存在执行器时变故障的系统,研究了非均匀传输NCS故障调节与通讯协同设计的问题.Ge和杨等[13-14]采用动态事件触发通信调度,根据实时情况动态调节数据是否发送,有效减轻了网络负担.上述研究表明,事件触发通信策略可以有效地降低网络通信负担,显著提高通信资源的利用率.此外,对于遭受DoS攻击的信息物理系统,事件触发机制在减轻通信负担的同时,也能够在一定程度上降低DoS攻击对系统性能带来的负面影响.Cheng等[15]提出了一种抗周期DoS攻击的弹性事件触发方案,但是该事件触发机制主要是为周期性DoS攻击设计的,对于具有一定随机分布特性的DoS攻击适用性不强.李炜等[16]结合事件触发通讯机制,研究了CPS双重安全控制与通讯的协同设计问题.Sun等[17]将DoS攻击引起的数据包丢失处理为触发条件的不确定性,将DoS造成的影响和事件触发机制有机结合,在保证系统性能的同时对DoS攻击具有良好的弹性,但该文并没有充分考虑系统所处物理环境的不确定性.在现阶段的研究中,研究者大多都是在DoS攻击以固定周期阻断系统通信的条件下,进行基于事件触发通信的系统控制问题研究,但针对一些攻击模式不确定的随机型DoS攻击,采用事件触发机制进行保证系统控制性能的研究还相对较少.

基于上述分析,本文针对受到随机DoS攻击的CPS,基于离散事件触发机制研究了系统的保性能控制问题.考虑了系统中存在的不确定性,建立了具有不确定性的离散系统模型,将DoS攻击行为建模为服从Bernoulli分布的随机过程,在此基础上借助Lyapunov稳定性理论和线性矩阵不等式方法给出闭环系统稳定的充分条件和保性能水平,并基于事件触发机制设计了系统保性能状态反馈控制策略,最后通过仿真实例验证了所提出控制方法的有效性.

1 问题描述

考虑DoS攻击下的一类CPS,其结构如图1所示.系统状态量测信号通过网络传送到控制器.零阶保持器ZOH的作用是使得控制器在没有接收到最新的状态信息时,保持最近一次控制器的输入不变,直到获得新的数据包.

图1 DoS攻击下的CPS结构Fig.1 CPS structure under DoS attacks

考虑具有不确定性的离散时间被控对象模型为

x(k+1)=(A+ΔA)x(k)+(B+ΔB)u(rk)

(1)

其中：x(k)∈Rn，u(rk)∈Rm分别表示系统的状态和控制输入；A、B分别是已知的适当维数常数矩阵；ΔA和ΔB分别为不确定性矩阵,表示系统模型中的参数不确定性.

为了便于分析,首先对CPS提出如下假设：

假设1，系统状态均为可直接量测的.

假设2，参数不确定性是范数有界的,并具有以下形式：

(2)

其中：F∈Ri×j是满足FTF≤I的不确定矩阵;D、Ea、Eb分别是反映不确定性结构的常数矩阵.

假设3，传感器是时间驱动周期采样的,采样周期为h.

参考文献[11]提出的离散事件触发通信机制,令e(rk)=x(k)-x(rk),则满足以下离散事件触发通信机制的采样数据允许通过网络传输：

eT(rk)Ue(rk)≥δxT(rk)Ux(rk)

(3)

其中：rk为事件触发时刻;U为触发矩阵；δ∈(0,1)是事件触发参数.则下一次数据传输的触发时刻为

rk+1=inf{k|eT(rk)Ue(rk)≥δxT(rk)Ux(rk)}

本文采用的基于离散事件触发机制的状态反馈控制器为

u(rk)=Kx(rk)

(4)

本文只考虑状态量测通道内的DoS攻击问题,当DoS攻击发生时会导致满足事件触发条件的状态量测数据包丢失,记rk为在控制器一侧当前收到的最新数据包时刻.

假设4，由于DoS攻击的影响,在接下来的rk+1,rk+2,…,rk+n时刻的满足事件触发条件的数据包会在传输过程中丢失,记n为DoS攻击造成的最大数据包连续丢失数.

传感器量测数据在传输过程中有可能遭受到DoS攻击,随机DoS攻击可描述为

(5)

αk是独立同分布的Bernoulli随机过程,满足：

Pr{αk=1}=p, Pr{αk=0}=1-p

由CPS结构图可知,满足传输条件的传感器量测数据在通信网络中进行传送.当测量信道遭受到DoS攻击后,控制器输入保持为最近一次DoS攻击发生前的事件触发时刻的状态.基于上述分析,考虑DoS攻击行为的状态反馈控制器(4)可以描述为

u(rk)=αkKx(rk)+(1-αk)Kx(rk-n)

(6)

综合考虑式(1,4,6),可得闭环系统模型为

(7)

将式(2)代入式(7),可得

x(k+1)=A1x(k)+B1e(rk)+B2x(rk-n)

(8)

其中：

A1=A+αkBK+DF(Ea+αkEbK)B1=αk(B+DFEb)KB2=(B+DFEb)K(1-αk)

结合上述闭环系统模型,考虑如下形式的二次型系统性能指标函数:

(9)

本文的目的是对事件触发机制(3)和状态反馈控制器(5)进行协同设计,从而实现闭环系统(8)的保性能控制,且获得给定二次型目标函数(9)的上界.

2 主要结果

本节首先给出DoS攻击下CPS稳定的充分条件,同时得到二次型目标函数的上界,再进一步求取所设计保性能控制器的参数矩阵.

引理1[18]给定适当维数的矩阵D、E和Y=YT,则

Y+DFE+ETFTDT<0

对所有满足FTF≤I的矩阵F成立,当且仅当存在一个常数ε>0,使得

Y+εDDT+ε-1ETE<0

定理1对于闭环系统(8),若存在矩阵K、对称正定矩阵P、G和U,使得对所有允许的不确定性,有以下矩阵不等式成立：

(10)

J≤J*=xT(0)Px(0)+xT(r-n)Gx(r-n)

(11)

其中:

则在事件触发机制(3)下的闭环系统(8)在随机DoS攻击下是鲁棒稳定的,且具有保性能水平J*.

证明选取李雅普诺夫Lyapunov函数:

(12)

其中:P和G为正定矩阵.显然对任意x(k)≠0,V(k)是正定的.沿闭环系统(8)的任意轨线计算V(k)的前向差分,并考虑事件触发条件(3),可得

ΔV(k)=V(k+1)-V(k)=

xT(k+1)Px(k+1)+

eT(rk)Ue(rk)+δxT(rk)Ux(rk)=

xT(k+1)Px(k+1)+

xT(rk)Gx(rk)-xT(k)Px(k)-

xT(rk-n)Gx(rk-n)-eT(rk)Ue(rk)+

δxT(rk)Ux(rk)

(13)

令

由式(13)可得:

由式(10)可得

(Θ+diag{Q+KTRK,0,0})<0

则有

V(k+1)-V(k)+xT(k)Qx(k)+uT(k)Ru(k)<0

即

ΔV(k)<-xT(k)(Q+KTRK)x(k)<0

(14)

可以得到闭环系统(8)是鲁棒稳定的.进而,对式(14)两边从k=0到k=∞求和,可得

由于系统是稳定的,可知V(x(∞))=0,于是有

xT(0)Px(0)+xT(r-n)Gx(r-n)

从而

定理得证.

定理2对于具有性能指标(9)的闭环系统(8),给定参数ε>0,在事件触发机制(3)下若存在矩阵W、对称正定矩阵X、M和H,使得以下矩阵不等式成立:

(15)

其中:

则可得到闭环系统(8)在随机DoS攻击下的离散事件触发参数U及鲁棒保性能控制器:

K=WX-1

(16)

且相应的保性能水平满足J≤J*.

证明矩阵不等式(10)可以写成

(17)

其中:

对式(17)应用舒尔补定理,可得

(18)

将A1、B1、B2的值带入式(18),可得

(19)

其中:

Λ12=A+αkBK

对式(19)应用引理1,可知存在一个常数ε>0,使得以下矩阵不等式成立:

(20)

对式(20)应用舒尔补定理,可得

(21)

其中：

Λ11=-P-1+εDDT

Λ13=(1-αk)BK

对式(21)分别左乘右乘合同矩阵diag{IP-1P-1P-1I},并记X=P-1,W=KP-1,H=P-1GP-1,M=P-1UP-1,S=P-1QP-1,Z=R-1,可得

(22)

对式(22)再次应用舒尔补定理,可得式(15),由证明过程可知式(16)成立.类似于定理1的证明,可得J≤J*.定理得证.

3 仿真实例

为了验证本文所提控制策略的有效性,参考文献[19]的RLC电路模型,被控对象的状态方程为

取C=0.5 μF,L=4 H,R=0.01 Ω.假设采样周期h=0.02 s,同时考虑到系统中的不确定性,则离散化后被控对象的状态方程为

x(k+1)=(A+ΔA)x(k)+(B+ΔB)u(rk)

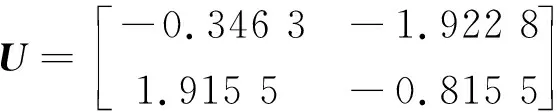
相应的保性能水平的上界为J*=27.763 9.

图2a是无DoS攻击时的事件触发时刻,图2b是无DoS攻击时网络化控制下的RLC电路的状态轨迹图.从图2a可以看出,本文所采用的离散时间触发通信机制达到了节约网络通信资源的目的.从图2b可以看出,本文所提出的保性能控制策略在无DoS攻击时可使系统迅速达到稳定状态.

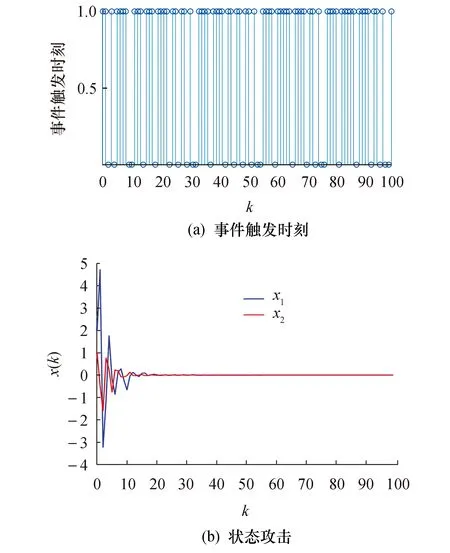
图2 无DoS攻击时的事件触发时刻和状态轨迹Fig.2 Event trigger time and state trajectory without DoS attacks

考虑到系统受到随机性DoS攻击,假设攻击造成的数据最大连续丢包数n=4.根据定理2可得系统遭受DoS攻击时的控制器增益和事件触发矩阵分别为

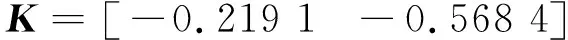
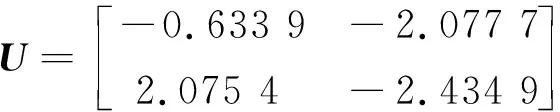
图3给出了DoS攻击概率为0.20的攻击时刻和有效事件触发时刻.从图3b可以看出,受到DoS攻击时会使部分满足事件触发条件的系统状态无法传输,相较于无攻击情况下的事件触发时刻,系统受到攻击时的有效事件触发次数显著减少,但仍然可以达到节约通信资源的目的.

图3 攻击概率为0.20的攻击时刻和有效触发时刻Fig.3 Attack time and effective trigger time with attacks probability of 0.2

图4给出了网络化控制下的RLC电路在受到随机DoS攻击下的状态轨迹.可以看出,本文所提出的保性能控制器在遭受到随机DoS攻击后,闭环系统仍然能保持稳定,系统状态在有限步数内收敛于平衡状态.

图4 攻击概率为0.20的状态轨迹Fig.4 State trajectory with attacks probability of 0.20

图5给出了系统受到DoS攻击概率为0.40的攻击时刻和有效事件触发时刻.通过对比不同攻击概率下的有效通信触发时刻可知,当攻击概率提高时会导致更多的量测数据无法到达控制器端.

图5 攻击概率为0.40的攻击时刻和有效触发时刻Fig.5 Attack time and effective trigger time with attacks probability of 0.40

图6给出了攻击概率为0.40时系统的状态轨迹.可以看到,当系统受到攻击概率为0.40的DoS攻击时,本文所提的控制策略仍然能够保证系统稳定.

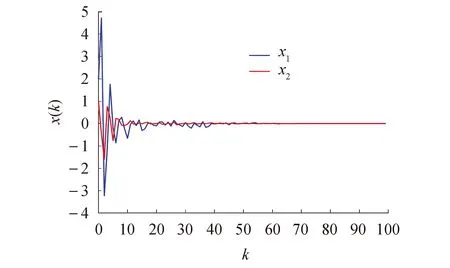
图6 攻击概率为0.40的状态轨迹Fig.6 State trajectory with attacks probability of 0.40

表1给出了保性能水平上界J*与随机DoS攻击概率的关系.从表1可以看出,随着通信信道出现DoS攻击,系统的性能指标上界随着攻击概率的提升逐渐增大,但是仍然可以保证状态的稳定.当攻击概率为0.6时,系统会出现不稳定的情况,这表明所设计的保性能控制器在一定的攻击强度下能够使得系统稳定运行.

表1 保性能水平上界J*与DoS攻击概率的关系Tab.1 The relation of upper bound J* for performance index and DoS attacks probability

4 结论

本文研究了随机DoS攻击下基于事件触发机制的信息物理系统安全控制问题.考虑到DoS攻击造成的数据丢包以及由于环境变化和元件老化等因素造成的系统参数不确定性,借助状态反馈控制律给出了闭环系统模型,基于Lyapunov稳定理论和线性矩阵不等式技术得到了闭环系统稳定的充分条件和保性能水平,求解出了保性能控制器与事件触发矩阵.最后,通过仿真实例验证了所提出控制方法的有效性.今后将在DoS攻击同时存在于测量信道和控制信道的条件下,进行CPS的安全控制问题研究.