具有收获和避难所效应的捕食—食饵系统Hopf分支分析
张道祥,李梦婷,闫 晴,周 文
(安徽师范大学 数学与统计学院,安徽 芜湖 241002)
引言
多年来,捕食-食饵系统动力学一直是生态学和生物数学的重要研究问题。在数学中,使用微分方程组来刻画捕食者与食饵之间的关系是一种主要的研究方法。20世纪50年代,Leslie首先提出了如下捕食-食饵模型[1-2]:

其中u,v分别表示食饵和捕食者的密度,m是捕食者的攻击率,a是食饵的内禀增长率,b是捕食者的内禀增长率代表食饵的环境容纳量代表捕食者依赖食饵的承载能力。
1960年,Leslie和Gower对系统(1)进行了改进,引入了功能反应函数[3]:

其中p(u)表示捕食者对食饵的功能反应函数。最著名的功能反应函数是Holling型,如HollingI-Ⅳ[4-8],它们仅依赖于食饵u的密度。其他学者又提出了同时依赖于食饵u和捕食者v密度的功能反应函数,如Beddington-DeAngelis,Crowley-Martin型等[9-12]。
Lou[13]进一步研究了具有Beddington-DeAngelis功能反应函数的Leslie-Gower型捕食-食饵系统:
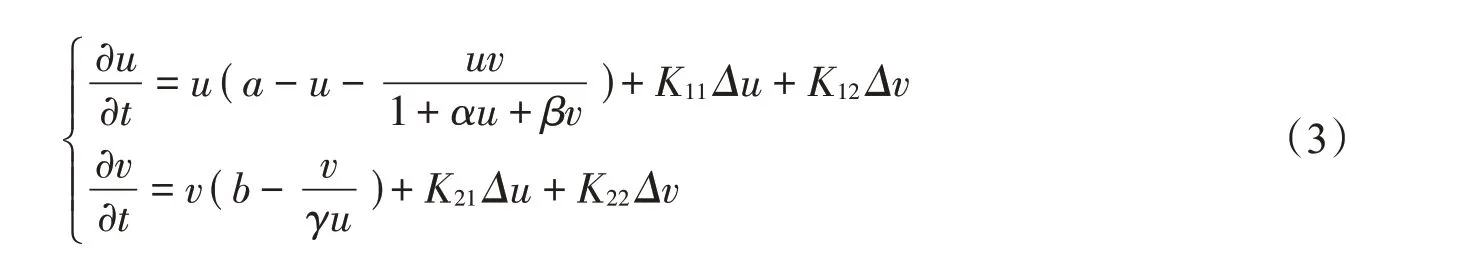
其中K11,K12,K21,K22是扩散系数,α,β分别表示食饵的饱和系数和捕食者的干扰系数。
近年来由于过度捕捞、污染以及渔业和林业等生物资源的商业开发不善等多种生态和经济因素,许多物种已经灭绝。为了更好地保护物种的多样性,带收获和猎物避难所效应的生物数学模型被大量研究[14-18]。Guin和Acharya[19]研究了一类如下具有比率依赖的捕食-食饵系统的空间动力学问题:

其中k1,k2,p,e,q,d分别表示食饵的环境容纳量,捕食者的环境容纳量,捕食率,转化率,食饵的线性收获率和捕食者的死亡率,c表示捕食者的干扰系数,m(0≤m<1)是猎物避难所效应参数。该文结果表明收获和避难所效应对物种空间斑图的形成具有重要的控制作用。
上述系统中的收获效应是线性的,然而在实际生产中并非如此。1976年,Clark提出了一种更符合现实情况的非线性收获效应,即Michaelis-Menten型收获项[20]:
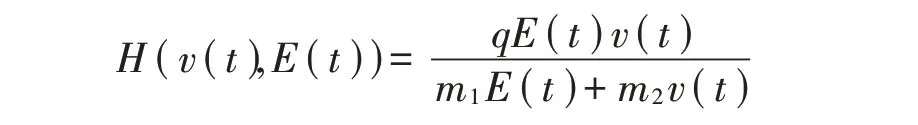
其中q,E分别表示收获能力和收获努力量,m1,m2是正常数。这种类型的收获在收获努力量和种群丰富度方面都表现出饱和效应,这对生态保护和管理具有重要作用。
本文主要考虑如下对捕食者具有非线性收获和食饵具有避难所效应的捕食-食饵模型:
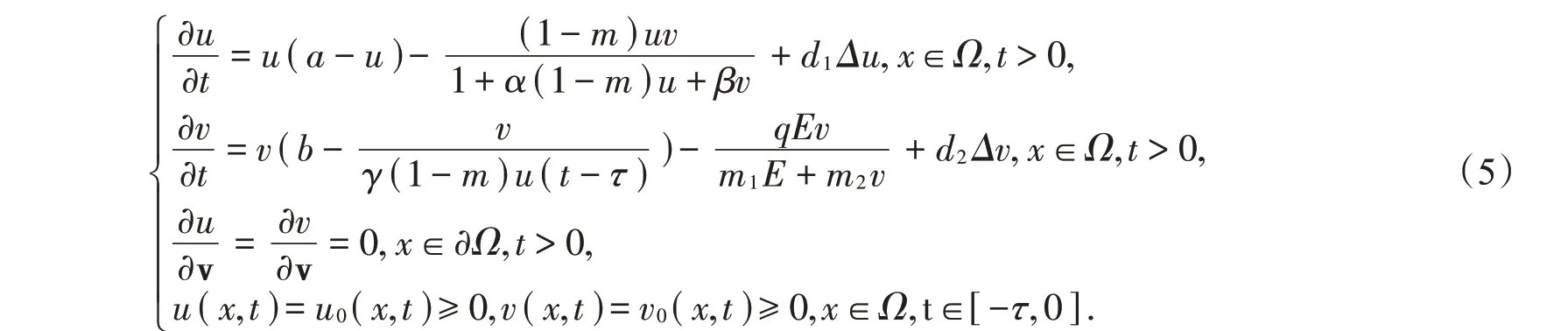
其中d1,d2是扩散系数,τ是时滞,(x,t)∈Ω×R+,Ω∈R2是边界光滑的有界区域,v是∂Ω上单位外法向量。为了简化模型,我们作如下变换于是系统(5)可化为:
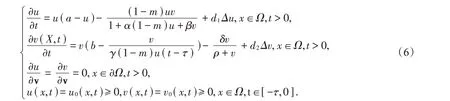
其不考虑时滞的常微分系统为:
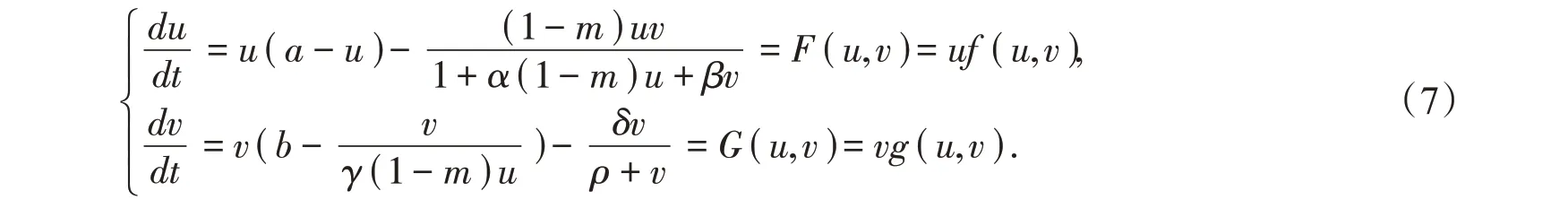
1 系统(7)解的正性、有界性及正平衡点的存在性
首先证明系统(7)的解的正性。
定理1.1系统(7)的所有具有正初始条件的解都保持为正。
证由于F(u,v),G(u,v)在R2+是连续的且满足局部Lipschitz条件,则解的存在性和唯一性定理保证了系统具有正初始条件的解都存在且唯一。由系统(7)可知:
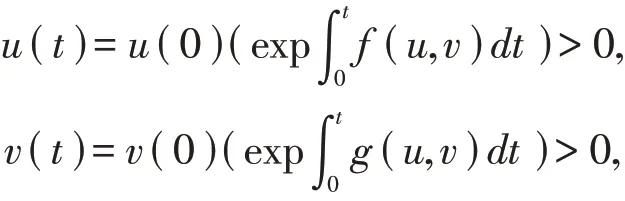
其中u(0)>0,v(0)>0是初始条件。显然,系统的解是正不变的。
接着证明系统(7)解的有界性。
引理1.1[21]若ξ,η>0且u(0)>0,则对于微分不等式≤u(t)(ξ-ηu(t))有:
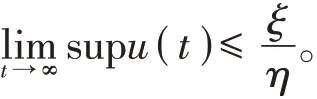
定理1.2系统(7)的所有始于R2+的解都是有界的。
证 根据系统可知≤u(a-u),由引理1.1可推出lti→m∞supu(t)≤a,
则对任意充分小的ε1>0,存在t1>0,使得
则对任意充分小的ε2>0,存在t2>t1,使得
综上可知定理成立。
考虑到系统(7)的生态学意义,接下来我们只研究系统(7)的正平衡点。由系统(7)可知正平衡点满足如下方程组:

我们作出如下假设:
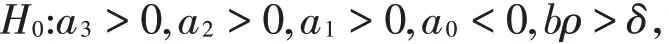
其中:
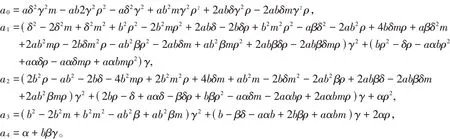
我们有如下定理:
定理1.3若满足条件H0,则系统(7)存在唯一正平衡点E*=(u*,v*)。
证 由方程g(u,v)=0,我们得出将其代入f(u,v)=0可得到v*满足下列方程:
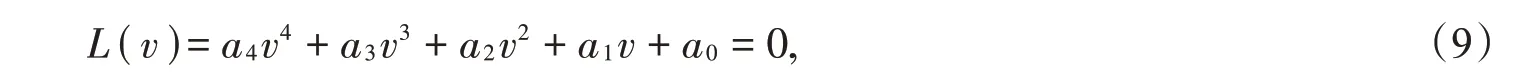
显然a4>0,若满足条件a3>0,a2>0,a1>0,a0<0,根据Descartes符号法则可知方程L(v)=0有唯一正解v*,再由可知当满足bρ>δ时,u*>0。所以当满足上述条件时,系统(7)存在唯一的正平衡点E*=(u*,v*)。
2 稳定性分析
2.1 ODE系统分析
由前面分析可知系统(7)存在正平衡点E*,在正平衡点E*处的Jacobian矩阵为:
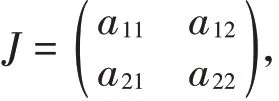
其中
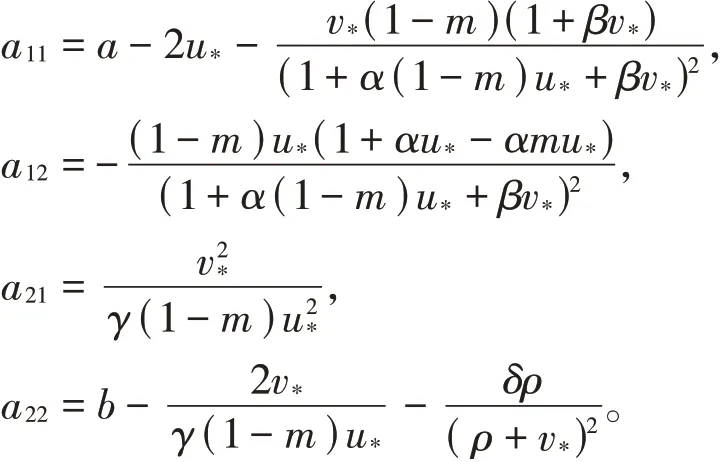
系统的特征方程为:
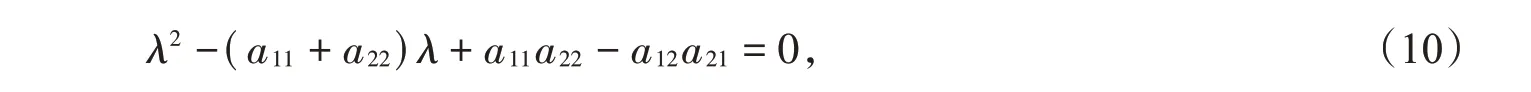
我们作出如下假设:H1:a11+a22<0,H2:a11a22-a12a21>0。
定理2.1.1若条件H0-H2成立,则系统(7)正平衡点E*是局部渐近稳定的。
注1结合上述定理可知,在不考虑时滞的情况下,由于条件H1,H2成立与否受δ的影响,故系统(7)的正平衡点的稳定性与δ有关。
定理2.1.2若满足条件H0,且α(1-m)2<β,则系统(7)的正平衡点E*在R2+的子集B={(u,v)∈R2+|δγu<ρv}中是全局渐近稳定的。
证 构造Lyapunov函数V=l1(u-u*-u*ln)+l2(v-v*-v*ln),其中l1,l2均为待定正常数,则函数V沿着系统(7)的全导数为:
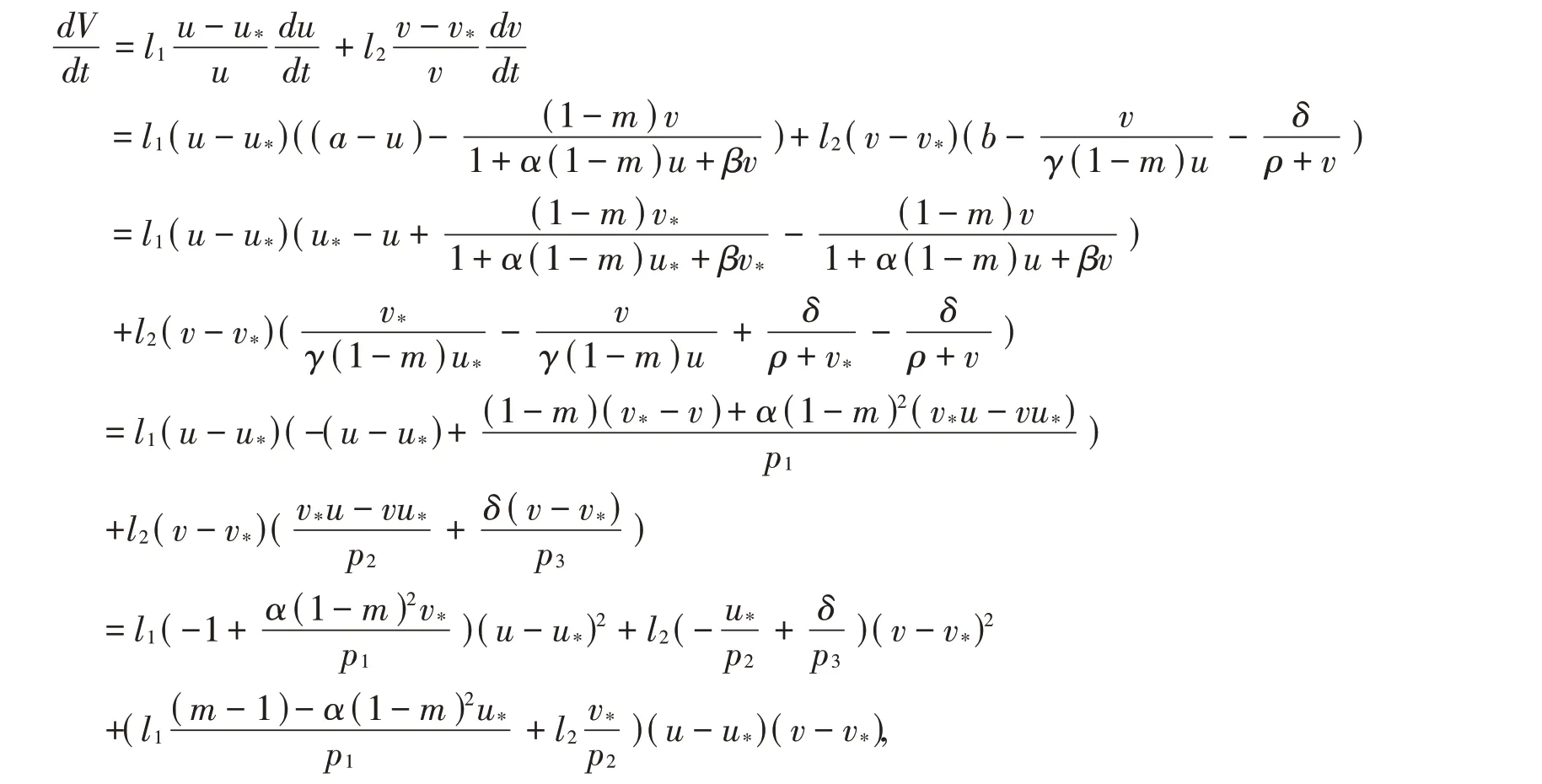
其中
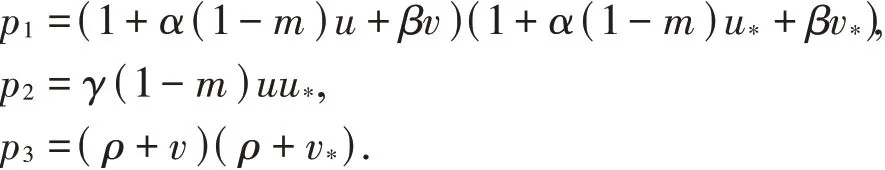
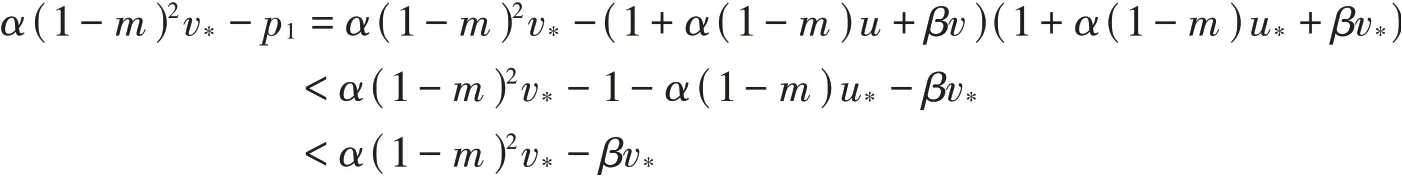
故 当α(1-m)2<β时,且δp2-u p3=δγ(1-m)uu-u(ρ+v)(ρ+v*)<δγuu*-u*ρv,
由此可知除在正平衡点E*外有<0,根据Lasalle不变集原理可知系统(7)的正平衡点E*在B中是全局渐近稳定。
注2可以看出,在没有收获效应,即δ=0时,只要满足α(1-m)2<β,系统的内部平衡点E*在R2+是全局渐近稳定的。
2.2 PDE系统分析
为了讨论系统(6)在正平衡点E*处的稳定性,首先在E*处引入小扰动:
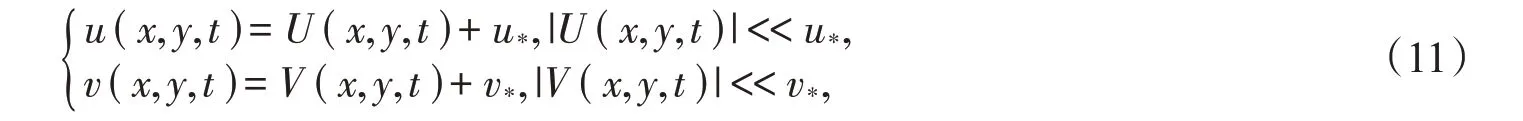
其中U(x,y,t)=U0eλtei(kxx+kyy),V(x,y,t)=V0eλtei(kxx+kyy);λ表示时间t处的扰动增长率;i表示虚数单位,kx,ky为相应的振幅,k=表示波数,且k∈N0={0, 1,2…},U0,V0为两个实数。
系统(6)在平衡点E*处的线性化方程为:
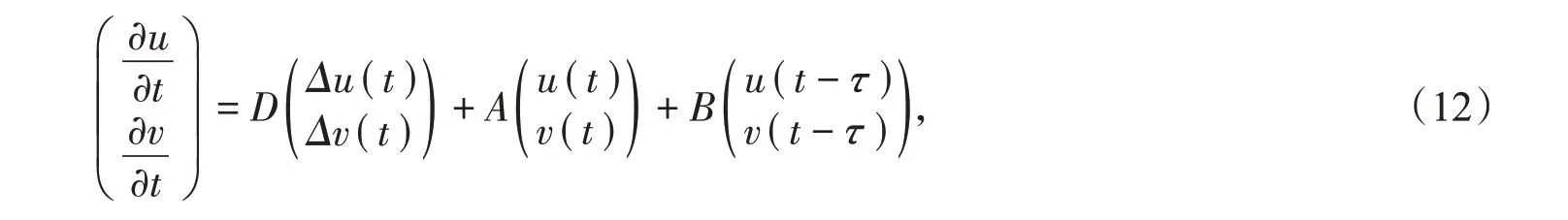
其中
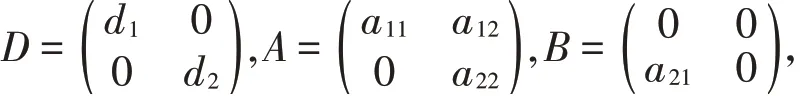
则系统(6)的特征方程为:

其中
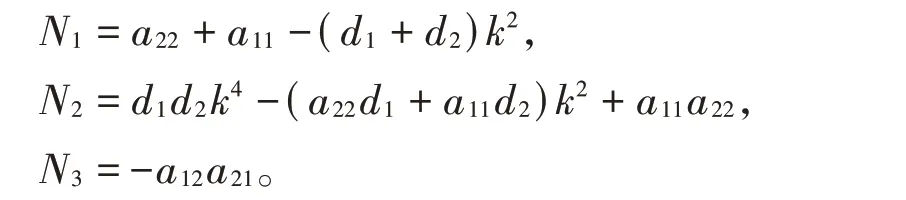
我们作出如下假设:
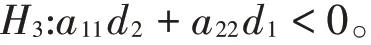
定理2.2.1对任意k≥0当τ=0时,若条件H0-H3成立,则系统(6)的正平衡点E*是局部渐近稳定的。证当τ=0时,特征方程(13)变为

H1成立,则N1<0,H2,H3成立,则N2+N3>0,
根据Routh-Hurwitz判据可知E*是局部渐近稳定的。
3 分支分析
3.1 ODE系统Hopf分支
这部分以δ为分支参数考虑系统(1.7)的Hopf分支的稳定性。
定理3.1.1当δ=δH满足trJ=0时,系统(7)在平衡点E*处发生Hopf分支的充要条件是
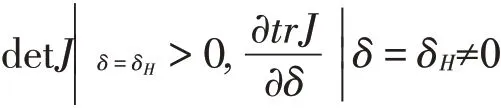
证trJ=0时,若detJ>0则特征方程(10)有一对纯虚特征值λ=±iθ,
其中θ2=detJ,下面考虑横截性条件。
记λ=ς+iζ,代入特征方程中并分离出虚实部得到:

上式中第二式两边同时对δ求偏导得:
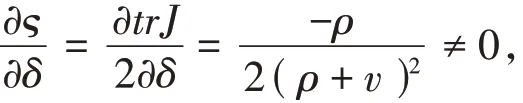
综上可知满足系统发生Hopf分支的条件,故上述定理成立。
3.2 PDE系统Hopf分支
这部分将时滞作为分支参数,分析系统(6)的Hopf分支问题。设λ=iω是方程(13)的纯虚根,则iω满足下列方程:
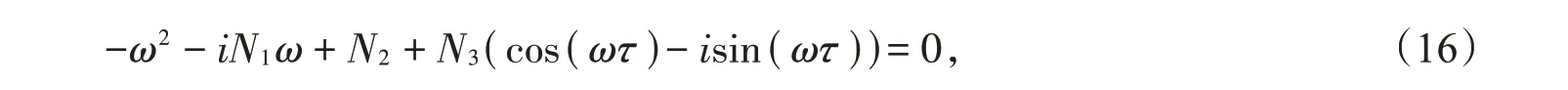
分离上述方程的实部与虚部,我们推出

将方程的左右两边平方再相加,得到

令ω2=z,方程变为:

做出如下假设:
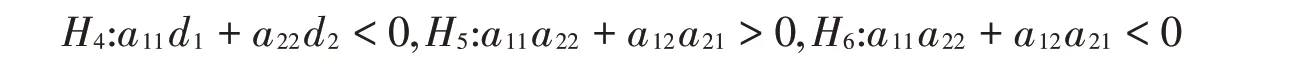
定理3.2.1对任意τ>0,k>0时,若条件H0,H2-H5成立,则系统(6)的正平衡点是局部渐近稳定的。
对于P=N22-N32=(N2+N3)(N2-N3),可知当H2-H3成立时N2+N3>0,
P的符号由N2-N3决定。由H3,H6可知存在N*∈N0使得
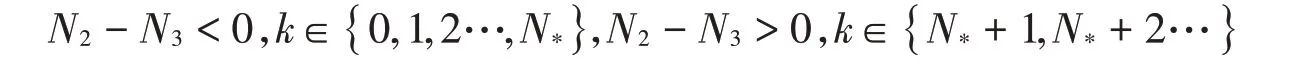
定理3.2.2若H0-H3,H6成立,则当k∈{ }
0, 1,2…,N*时方程(18)有唯一的正根ω+。
引理3.2.1若H0-H3,H6成立,
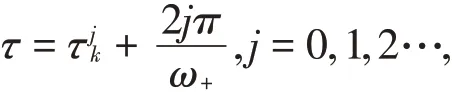
特征方程有一对纯虚根±iω+,其中
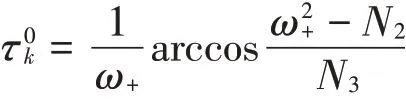
引理3.2.2 H0-H3,H6成立,τjN*≥τjN*-1≥τjN*-2≥…≥τj1≥τj0,j=0,1,2…,显然
引理3.2.3令λ(τ)=θ0(τ)+iθ1(τ)是方程(13)的根,当τ=τjk时θ0(τjk)=0,θ1(τjk)=ω+,如下横截性条件成立:
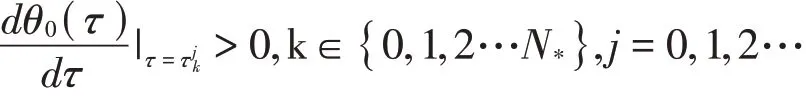
证
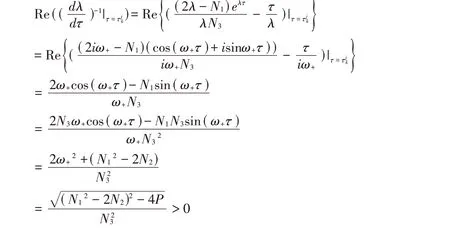
定理3.2.3若H0-H3,H6成立,有下述命题成立:
(i)当τ∈[0,τ00)时,系统(6)的平衡点E*=(u*,v*)是局部渐近稳定的;
(ii)当τ∈(τ00,+∞)时,系统(6)的平衡点E*=(u*,v*)是不稳定的;
通过以上稳定性分析和分支理论[22],得到如下系统(6)的Hopf分支曲线图,见图1。图1中,子图(a)展示了m=0.26时δ-τ关系图,可以看出δ越大,Hopf分支的临界值τ00越大,即收获效应与系统(5)的正平衡点的稳定区间呈正相关。子图(b)展示了δ=0.02时m-τ关系图,可以看出m越大,分支的临界值τ00越大,即猎物避难所效应与系统(5)的正平衡点稳定区间呈正相关。
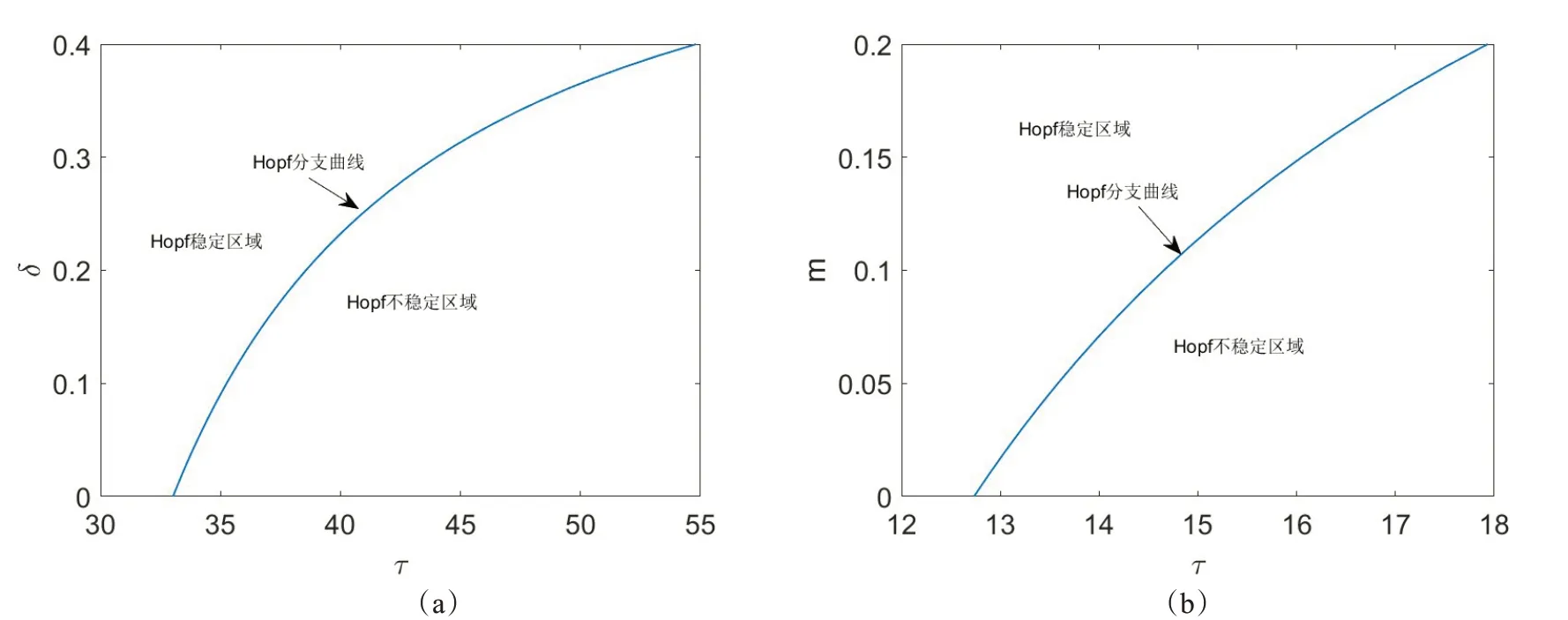
图1 系统(5)Hopf分支曲线图参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,d1=0.005,d2=0.005.(a)δ-τ关系图,(b)m-τ关系图Fig.1 Bigfurcation diagram of system(5)with a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,d1=0.005,d2=0.005.(a)δ-τ,(b)m-τ
4 数值模拟
在这一部分,我们使用MATLAB软件进行数值模拟,以此来验证理论推导所得到的结论。
4.1 平衡点的稳定性
首先考虑常微系统(7)正平衡点的稳定性,选取满足条件H0-H2的参数为:a=0.5,b=0.5,α=1,β=1,ρ=0.1,δ=0.01;m=0.1,γ=1,图2展示了在该参数条件下系统相图和方向场,可看出此时系统的正平衡点E*=(0.4016,0.1672)是局部渐近稳定的,符合定理2.3.1的结果。
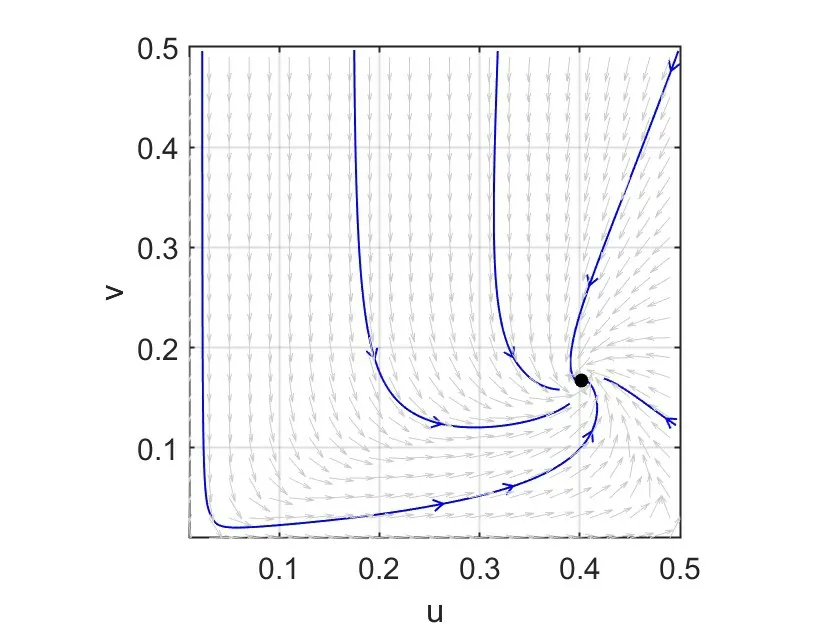
图2 系统(7)的相图和方向场参数:a=0.5,b=0.5,α=1,β=1,ρ=0.1,δ=0.01;m=0.1,γ=1,Fig.2 Phase diagram of system(7)with a=0.5,b=0.5,α=1,β=1,ρ=0.1,δ=0.01;m=0.1,γ=1,
接着考虑常微系统(7)正平衡点的全局稳定性,选取参数
接着考虑具有时滞的偏微系统(6)正平衡点稳定性。参数取为:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,通过计算可得平衡点E*=(0.0649,0.3023),Hopf分支临界值τ00=34.0402。图3展示了时滞τ取不同值时食饵和捕食者随时间的密度演化图。图3中,子图(a)表示时滞为τ=32∈[0,τ00)时的食饵和捕食者的密度演化图,图中食饵和捕食者密度值几乎不变,且数值均为平衡点的值,即u=0.0649,v=0.3023,这表明系统的正平衡点E*是渐近稳定的。子图(b)表示τ=35.6∈(τ00,+∞)时的食饵和捕食者的密度演化图,图中在t>10000时,食饵和捕食者的密度均呈振幅相同的波状,这符合Hopf分支现象,系统的正平衡点E*是不稳定的,这验证了定理3.2.3的理论结果。图4展示了时滞τ取不同值时捕食者与食饵的相图。图4中子图(a)表示时滞为τ=32∈[0,τ00)时的相图,相图表明随着时间的改变,食饵和捕食者的密度值逐渐趋向一个点( )0.0649,0.3023,且该点即为正平衡点E*,这充分说明,此时系统(6)在正平衡点E*处呈稳态。图4中子图(b)为时滞τ=35.6∈(τ00,+∞)时,相图呈现为极限环,这证明τ0附近会出现Hopf分支现象,进一步证实了理论结果。
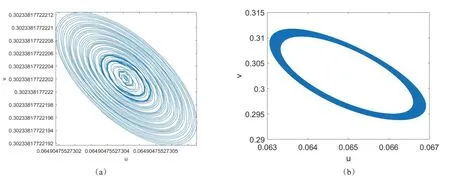
图4 系统(5)捕食者与食饵的密度演化图参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005.(a)τ=32,(b)τ=35.6Fig4 Time evolution curve of the predator and prey of system(5)with a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005.(a)τ=32,(b)τ=35.6
4.2 时滞对系统稳定性的影响
4.2.1 一维空间Hopf分支这部分参数设置同上。根据定理3.2.3可知,τ=τ00时系统(6)在平衡点E*处发生Hopf分支,当τ>τ00时平衡点会变得不稳定。图5和图6展示了随着τ增大,平衡点E*由稳定态变为不稳定态。
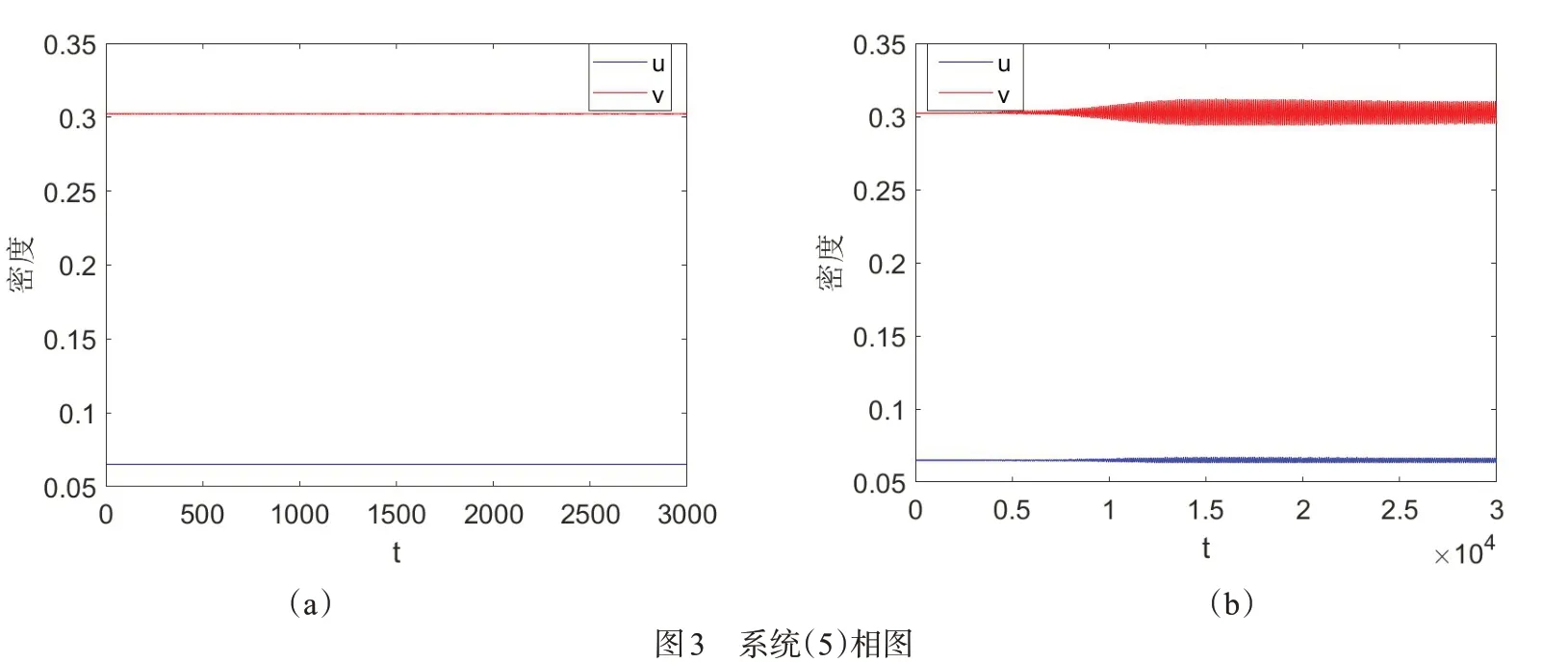
参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005.(a)τ=32,(b)τ=35.6Fig.3 Phase diagram ofsystem(5)with a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005.(a)τ=32,(b)τ=35.6
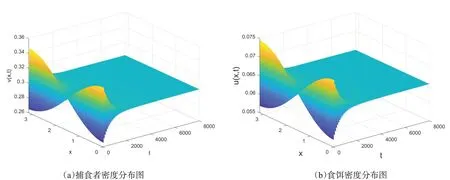
图5 系统(5)的捕食者与食饵的密度分布图参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=32.Fig.5 Density profile of the predator and prey of system(5)with a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=32.
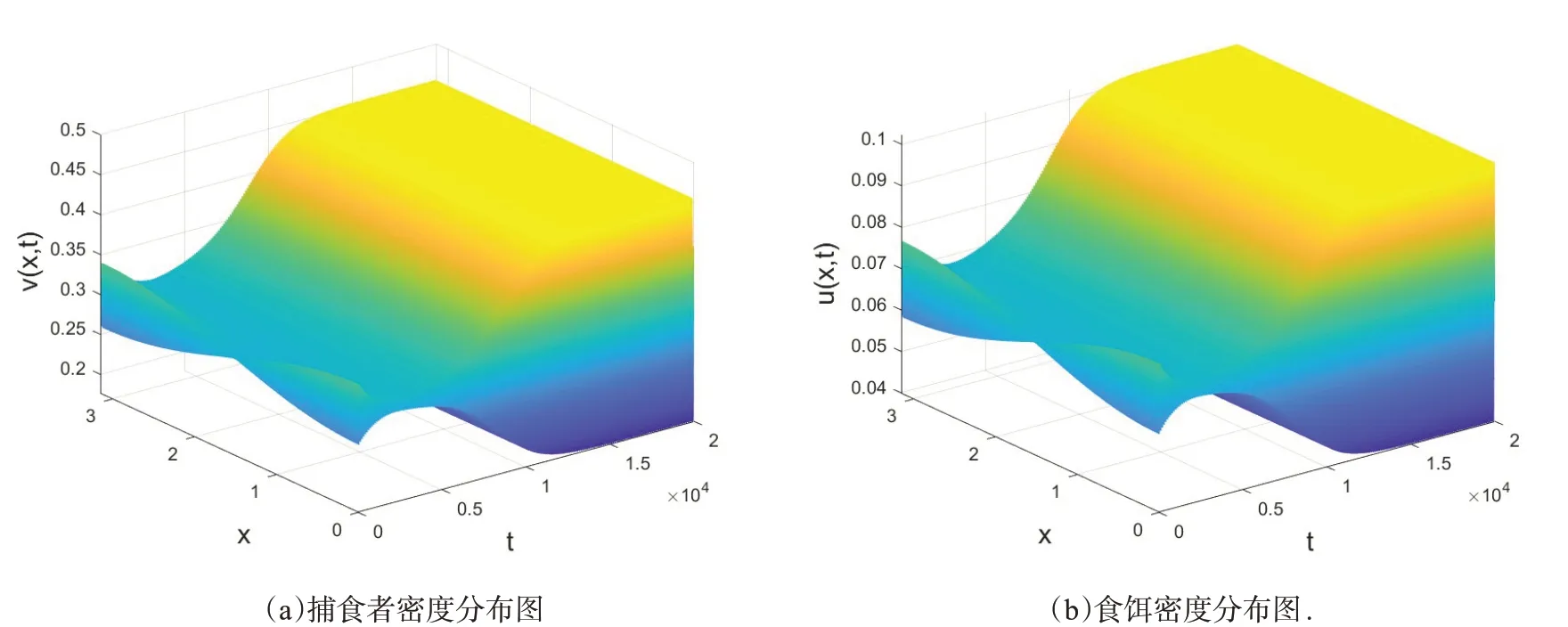
图6 系统(5)的捕食者与食饵的密度分布图参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=35.6.Fig.6 Density profile ofpredator and prey of system(5)with:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=35.6.
4.2.2 二维空间斑图这部分参数设置同上。由于食饵和捕食者的空间斑图是类似的,所以此处仅给出捕食者的空间斑图。
图7和图8展示了仅时滞τ取不同值时系统(6)的空间斑图演化过程,其中各子图右侧的条状图可作为捕食者密度值的参照。图7是τ=32时的情况,各子图分别展示了(a)t=0,(b)t=2000,(c)t=130000,(d)t=250000时刻下的空间密度分布图,且参照密度分布参照条可知捕食者的密度约为0.3023与正平衡点v*=0.3023相同,符合理论分析的结果,进一步证实了系统的正平衡点呈稳态。图8是τ=35.6时的情况,各子图分别展示了(a)t=0,(b)t=14000,(c)t=70000,(d)t=420000时刻下的空间密度分布图,这时E*是不稳定的,且随着时间的变化规则的螺旋波逐渐形成。
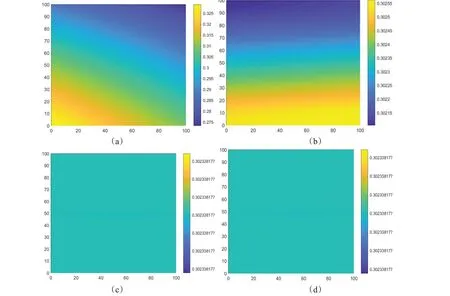
图7 系统(5)的捕食者的空间斑图参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=32.(a)t=0,(b)t=2000,(c)t=130000,(d)t=250000.Fg.7 Spatial pattern of the predator ofsystem(S)with a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=32.(a)t=0,(b)t=2000,(c)t=130000,(d)t=250000.
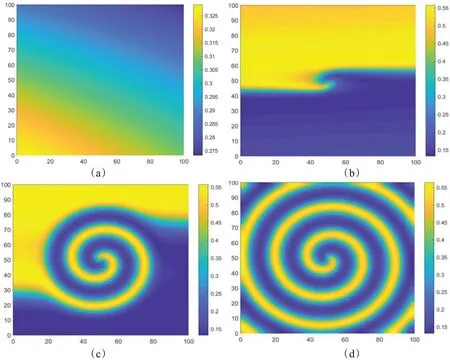
图8 系统(5)的捕食者的空间斑图参数:a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=35.6.(a)t=0,(b)t=14000,(c)t=70000,(d)t=420000.Fig.8 Spatial pattern of the predator of system(5)with a=0.2,b=0.6,α=1.7,β=1.9,ρ=1.5,m=0.26,γ=11,δ=0.05,d1=0.005,d2=0.005,τ=35.6.(a)t=0,(b)t=14000,(c)t=70000,(d)t=420000.
4.3 收获与避难所效应对密度的影响
这部分考虑收获与避难所效应对捕食者与食饵密度大小的影响。图9展示了不同收获效应参数下避难所效应对捕食者和食饵在平衡时密度的影响。可以看出在避难所效应参数一定时,收获效应参数越大,捕食者密度越小,食饵密度越大。即收获效应会降低捕食者的密度,提高食饵的密度。还可以看出避难效应参数越大食饵的密度越大,且在一定范围内避难所效应参数越大捕食者密度越大,这说明避难所效应不但会保护食饵也会对捕食者产生一定的保护作用。当避难所效应参数过大时会降低捕食者的密度。在实际生产应用中可通过调节避难所来保护捕食者与食饵。
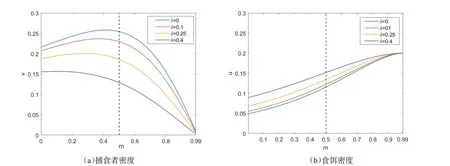
图9 收获与避难所效应对捕食者与食饵密度的影响参数:a=0.2,b=0.4,α=1.71,β=1.61,ρ=1.5,γ=11.Fig.9 Diagran ofpredator and prey density with a=0.2,b=0.4,α=1.71,β=1.61,ρ=1.5,γ=11.
5 结论
基于收获效应和避难所效应对捕食-食饵系统动力学行为有重要影响,本文从理论和数值模拟两方面研究了具有收获和避难所效应的捕食-食饵系统的稳定性和Hopf分支。结果表明:(1)无论有无时滞,收获都会影响系统的稳定性;(2)以时滞为分支参数时,收获和避难所效应均会影响分支的临界值τ00,并且在一定参数条件和区间内,收获和避难所效应参数的增加都会导致临界值变大;(3)收获效应会提高食饵的密度,降低捕食者的密度;(4)避难所效应会对食饵产生保护作用,且在一定范围内对捕食者有保护作用。

