有源智能反射面辅助大规模MIMO 波束成形方案*
刘依依,鲍 慧
(华北电力大学,河北 保定 071003)
0 引言
被动可重构智能反射表面(Intelligent Reconfigurable Surfaces,IRS)由大量低成本无源反射元件组成,其中每个元件都可以独立地调整反射信号的相移和幅度,从而能够改变无线信道环境,提高接收端的信号质量[1-4]。大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)技术和IRS 技术相结合,可以在不增加系统发送功率以及带宽的情况下,进一步提高用户的传输速率[5-6]。然而,IRS 反射链路具有“双重衰落”的问题,即通过此反射链路到达接收端的信号经历了两次大规模衰落,这极大地限制了IRS 的性能。
为了克服双重衰落,文献[7]提出了有源IRS的结构。不同于传统被动IRS,有源IRS 可以主动放大信号,因此可以通过调整放大倍数以及相移,进一步提高用户速率。结果表明,在功耗相同时,文献[7]提出的有源IRS 方案能够达到比传统无源IRS 方案更高的速率。文献[8]研究了有源IRS 辅助的单用户系统,分析了各种系统参数对有源IRS 的影响,并比较了主动IRS 和被动IRS 在不同条件下的表现。然而,有源IRS 在放大信号时引入了额外的噪声,这是限制有源IRS 性能的重要因素[9-10]。为了在最大化信号功率和最小化IRS 噪声之间取得平衡,本文提出了有源IRS 辅助大规模MIMO 的波束成形方案,利用连续凸逼近(Successive Convex Approximation,SCA)算法,在满足相位和功率约束条件下,通过联合优化基站和IRS 处的波束成形,得到最大化用户和速率的最优解。
1 系统模型
如图1 所示,考虑有源IRS 辅助大规模MIMO的通信系统,其中,存在一个天线数为M的基站,一个元件数为N的IRS 以及K个单天线合法用户。令hk∈CM×1,F∈CN×M,gk∈CM×1分别表示从基站到用户k、从基站到有源IRS 以及从有源IRS到用户k的信道;Θ∈CN×M为IRS 相移矩阵;xk为用户k的传输符号;wk为用户k的波束形成向量;z~CN(0N,σz2IN)为有源IRS 产生的动态噪声;nk~CN(0,σ2)为用户k处的高斯白噪声。

图1 有源IRS 辅助大规模MIMO 系统
则用户k接收到的信号可以建模为:

得到用户k的信号速率为:
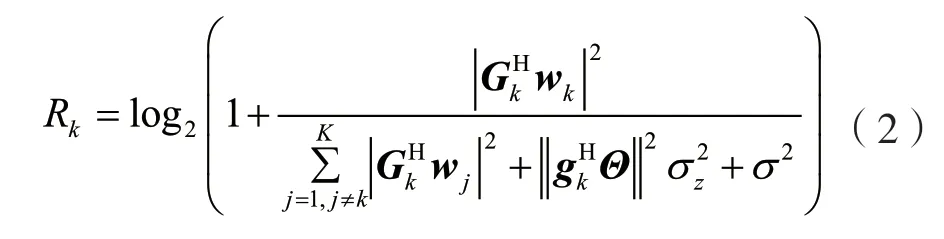
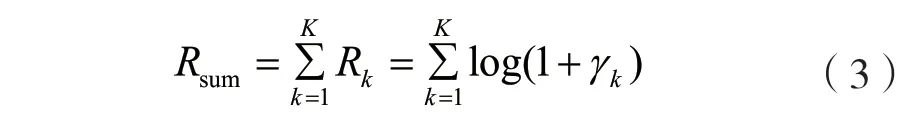
式中:γk为用户k处的信干噪比。通过联合优化基站波束成形向量和IRS 处的反射因子,可以最大化系统的和速率,优化问题可表示为:
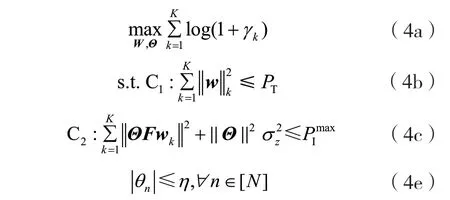
式中:W=[w1,…,wk];η是反射元件最大的放大因子;PT为基站发射功率限制;PImax为IRS 功率限制;θn为IRS 第n个元件角度。其中,(4b)和(4c)为基站和有源IRS 处的功率约束,(4e)为有源IRS的放大倍数约束。
2 联合波束成形设计
为了解决优化问题(4),本文首先将其分解为两个优化子问题,即基站预编码W优化子问题以及有源IRS 反射因子Θ优化子问题。
2.1 基站预编码W 优化子问题
固定Θ,优化基站预编码W,则优化问题变为:
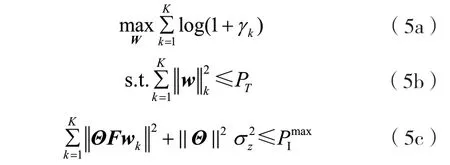
由于目标函数的非凸性,原问题是一个非凸问题。首先通过引入辅助变量α=[α1,…,αk]T解决对数函数,将优化问题(5)中的目标函数转换为:

式(6)通过令αk=γk可以证得,该步骤使得用户和速率最大化问题等价于信干噪比最大化问题。接着,引入分式规划辅助变量β=[β1,…,βk]T化简式(6)中的多比分式函数,将其分子分母解耦,可得到新的目标函数表达式:
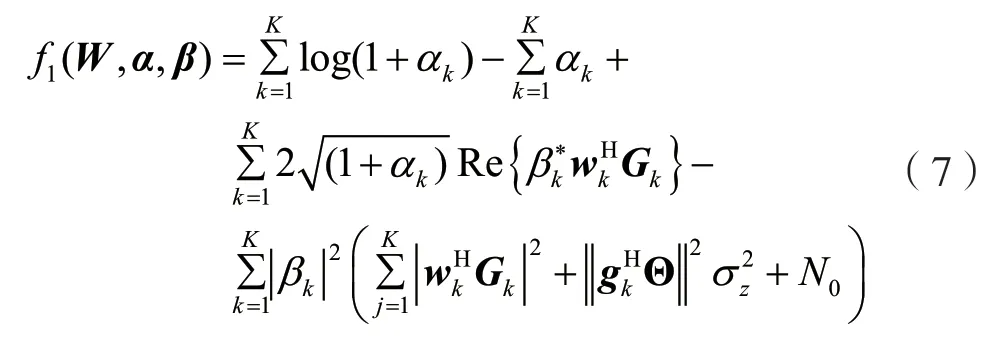
则问题最终可表示为:
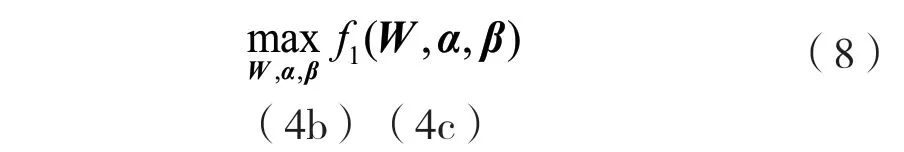
其中,对于固定的W和α,最优的β可以通过求导获得,求导公式为:
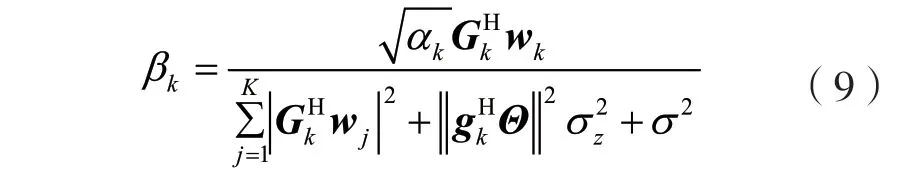
此时,问题(8)为凸优化问题,可利用SCA算法解决,得到基站预编码W优化子问题的最优解。
2.2 有源IRS 反射因子Θ 优化子问题
固定W,优化有源IRS 的预编码矩阵Θ,则优化问题变为:
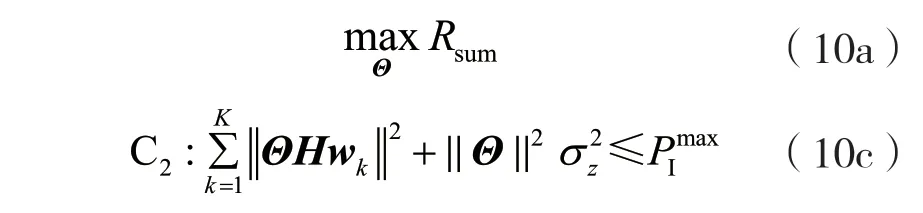

优化问题的非凸性仍然来源于目标函数。利用SCA 算法,通过与问题(5)一样的解决方案,可以获得问题(10)关于有源IRS 预编码矩阵Θ的解。通过交替迭代算法求解子问题(5)和(10),最终可以获得最大化用户和速率的最优解。
3 复杂度和收敛性
在整个迭代过程中,由于SCA 算法具有收敛特性,因此在交替优化发射端的波束形成矢量和IRS处的相移矩阵时,对于每一个优化子问题,均能保证其第j+1 次迭代后得到的优化目标值总是不小于第j次迭代后的目标值,即每次迭代所产生的值是单调非递减的。同时,由于发射总功率的限制,整个迭代过程是有限的,因此保证了算法的收敛性。
算法的复杂度由求解子优化问题(8)和(10)产生。令d1和d2分别为子优化问题每次迭代次数,其复杂度可分别由O(d1M4.5log(1/ς))和 O(d2N4.5log(1/ς))表示;因此,最大化用户和速率问题的总复杂度为O(d3O(d1M4.5log(1/ς)+d2N4.5log(1/ς)))。其中d3为优化问题(4)收敛所需的迭代次数,ς为设置的收敛精度。
4 仿真分析
通过MATLAB 对有源IRS 辅助大规模MIMO系统进行仿真,并对仿真参数进行设置。设基站和IRS 分别位于(0 m,0 m)和(80 m,10 m),用户随机分布在以(60 m,0 m)为圆心、半径为10 m 的圆圈内。假设所有的信道均服从瑞利衰落模型,将有源IRS 到合法用户k的信道建模为gk=rkPLgk,其中rk为瑞利小尺度衰落,表示路径损耗,ζ是单位距离上的信道增益,lrk为有源IRS到合法用户k之间的距离,λrk=3.5 为有源IRS 到合法用户k之间的路径损耗指数。基站到用户、基站到IRS 的信道模型与有源IRS 到合法用户k的信道模型类似,且将路径损耗指数分别设置为λBk=3.5,λBR=2.2。除非特别说明,设发射端天线数M=64,合法用户数K=4。基站和有源IRS 处的最大功率均设为30 dBm,有源IRS 的放大因子η2为20 dB,噪声功率设置为-80 dBm。
图2 所示为不同IRS 反射元件数与和速率的关系,并比较了有源IRS 与传统IRS 的性能。可以观察到,用户和速率随着元件数量的增加而增加,且本文提出的有源IRS 的方案比传统被动IRS 方案表现出更好的性能。有源IRS 在N=5 时的用户和速率已经超过被动IRS 在N=30 时的用户和速率。结果表明,与被动IRS 相比,有源IRS 可以节省更多的反射元件,从而大大降低IRS 的复杂性。此外,更少的元件数使得有源IRS 的表面积更小,更适合空间受限的场景。

图2 IRS 反射元件数与和速率的关系
图3 给出了系统和速率与基站的最大传输功率的关系,其中有源IRS 元件个数为10。可以观察到,系统和速率随着基站最大发射功率的增加而增加,且增加速度逐渐变缓。这是由于基站发射功率较小时,有源IRS 的功率约束并不起作用,可以轻松放大信号。而当基站发射功率较大时,有源IRS需要消耗更多功率来放大信号,此时有源IRS 辅助MIMO 系统受到放大功率约束的限制。此外,IRS放大因子较大时,系统具有更好的性能,且可以降低基站处消耗的发射功率。从图3 中可以得知,当基站发射功率为34 dBm 时,有源IRS 的和速率比被动IRS 的和速率高11.6%。在未来有源IRS 设计中,放大因子和IRS最大功率都需要根据实际情况仔细设计。
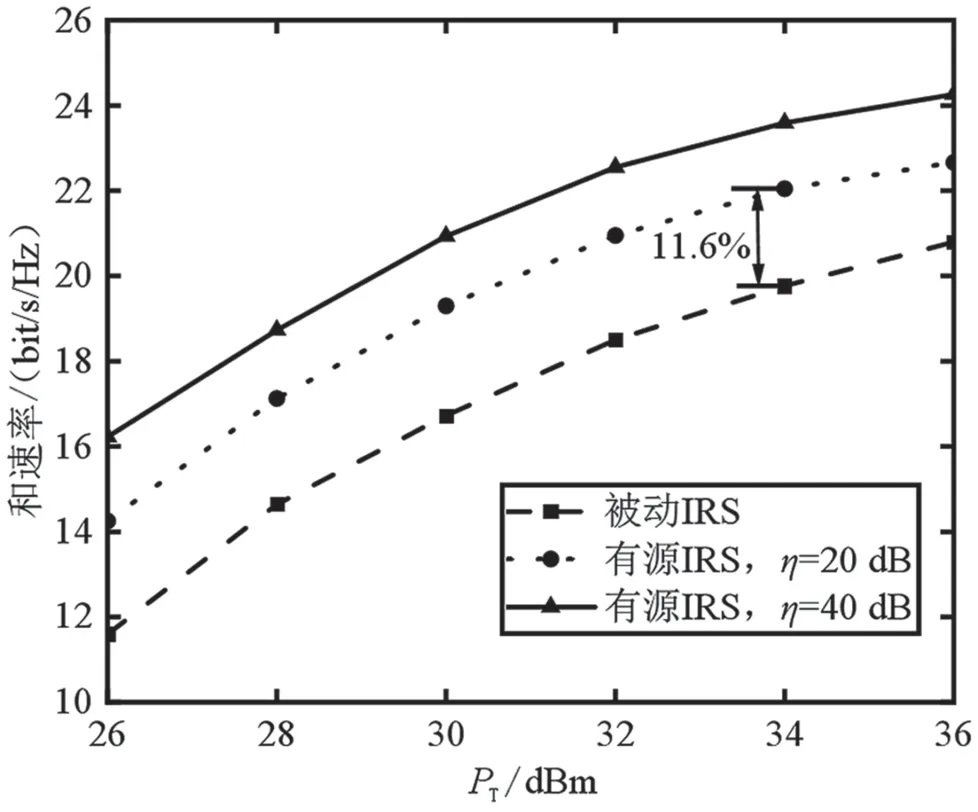
图3 和速率与基站最大传输功率的关系
图4 显示了系统和速率与合法用户数量的关系,其中有源IRS 元件个数为10。可以观察到,有源IRS 和被动IRS 的和速率随用户数量单调增加,但增长速率逐渐变慢,这是由于用户之间的干扰以及功率限制的存在。

图4 和速率与合法用户数量的关系
由图2 可知,当用户数为5 时,有源IRS 的和速率比被动IRS 高15.7%,有源IRS 很好地解决了被动IRS 的双重衰落效应。
5 结语
本文提出了一种基于有源IRS 的波束成形设计方案。首先,通过研究表明,利用有源IRS 辅助大规模MIMO 进行通信传输,可以有效地降低双重衰落效应的影响,减少系统功率消耗,提高系统速率性能;其次,通过调整基站和IRS 处的波束成形,在功率和IRS 相位的约束下,利用连续凸逼近算法和交替迭代算法得到了最大化用户和速率的最优解。仿真结果表明,与传统被动IRS 相比,有源IRS 在空间受限等场景具有很大潜力。此外,本文研究表明,在未来有源IRS 设计中,放大因子和IRS 都是值得考量的因素。

