基于多窗谱估计与NLMS 自适应滤波算法的单通道语音增强*

孙逸飞，涂振宇，相敏月，马 飞，方 强

（南昌工程学院 信息工程学院，江西 南昌 330099）

0 引言

语音在许多应用中有着重要作用，但由于背景噪音的存在且噪音具有多种多样的形式，获取清晰的语音变得困难，而语音增强技术旨在改善语音质量，提高语音可懂度[1]。

语音增强技术一直是语音信号处理领域的研究热点。Schroeder 实现了基本谱减法[2]（Spectral Subtraction，SS），改善了语音质量，但存在大量“音乐噪声”，降低了可懂度。在此基础上，Boll[2]提出了改进谱减法，但还存在少量“音乐噪声”。针对音乐噪声的问题，Thomson[3]提出了基于多窗谱估计的改进谱减法，音乐噪声基本得到消除。Ephraim[4]提出了基于最小均方误差估计（Minimum Mean Square Error，MMSE）的短时幅度谱估计法，但对非平稳噪声的抑制能力较弱。维纳滤波是对平稳信号的最小均方误差估计，语音为非平稳[4-5]，因此基于最小均方算法（Least Mean Square，LMS）的自适应滤波方法可以应对非平稳的信号。如今，深度学习在单通道语音降噪上实现[6]，语音增强技术进一步发展，但即使神经网络不断改进提升，也未能做到将某些非平稳的噪声滤除，反而还增加了训练优化的成本，因此有必要将传统的信号处理方式与深度学习相结合。联合优化既可以减轻网络的复杂度，也可以达到较好的语音增强效果[7-8]。

本文重点研究多窗谱估计与NLMS 自适应滤波的单通道语音增强，分别在不同噪声环境下、不同信噪比下的白噪声与有色噪声下进行对比实验，改进以往实验环境下噪声缺乏多样性且评价指标单一的问题，以语音质量指标如语音质量的感知评估（Perceptual Evaluation of Speech Quality，PESQ）及语音可懂度指标短时客观可懂度（Short-Time Objective Intelligibility，STOI）为标准，全面衡量其增强效果。

1 谱减法原理

1.1 基本谱减法

基于语音信号的非平稳特性，在时域中处理较为困难，因此将其转到频域进行短时特性分析。利用语音的短时无话段估计噪声谱，再从含噪语音的短时谱中减去估计出的噪声谱，得到纯净语音的短时谱，最后通过傅里叶逆变换恢复为时域信号[9-10]。

设语音信号为x(n)，噪声序列为d(n)，带噪语音表示为：

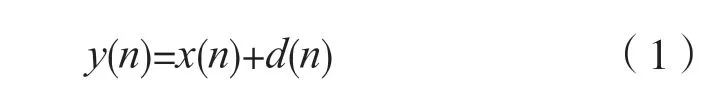
对y(n)，x(n)和d(n)进行分帧、加窗处理。已知前导无话段时长为IS，对应的帧数为NIS，估计噪声功率谱为：

式中：Xi(k)为语音信号的频谱，下标i表示第i帧。

传统谱减算法为：

式中：a和b是两个常数，a为过减因子，b为增益补偿因子[5,11]。由此得到原始语音的估计值，最后通过傅里叶逆变换恢复时域信号。

1.2 改进的谱减法

本文用于减少“音乐噪声”的方法是改进的谱减方法，即过减法（Overspectral subtraction，OSS）技术[2,6]，其改进的方面有以下3 个。

（1）谱减幅值或功率。基本谱减法是按功率谱计算的，使用了噪声段的平均功率谱如下：

式中：γ=1 或2，γ=1 时为幅值谱减法，γ=2 时为功率谱减法；α和β同基本谱减法的a和b。

（2）平均谱值。每帧信号x(m)做离散傅里叶变换（Discrete Fourier Transform，DFT）后得：

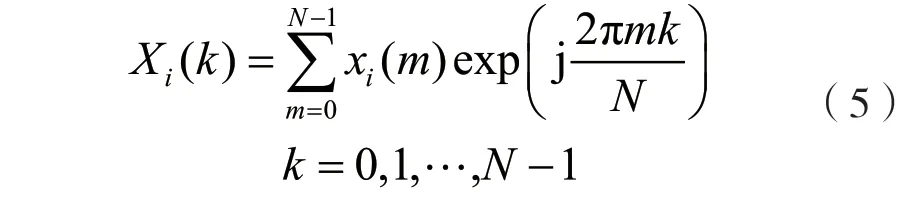
然后在相邻帧之间计算平均值：

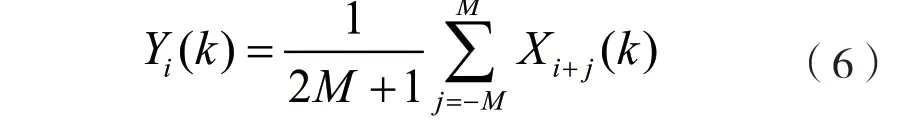
（3）噪声残留。因为噪声的随机性，谱减后部分噪声没有办法完全消除，所以在减噪中保留噪声的最大值，从而在谱减中尽可能减少噪声残留[10]。

2 多窗谱估计与NLMS 自适应滤波

2.1 多窗谱估计谱减

由于传统的周期图法只用一个数据窗，因此由Thomson 提出的多窗谱估计比周期图法更准确[12]。在实际语音处理中，可根据实际情况选择不同的窗函数。

多窗谱定义为：

式中：x(n)为数据序列；N为序列长度；ak(n)为第k个数据窗。

多窗谱估计改进谱减算法流程如下：

（1）对带噪的语音信号进行预处理，加窗分帧得到xi(m)。

（2）进行傅里叶变换，以i为中心，前后各取M帧，共2M+1 帧，得到Xi(k)，具体的计算式为：

（3）多窗谱估计，得到P(k,i)，其表达式为：

（4）计算平均功率谱为：

（5）计算噪声平均功率谱Pn(k,i)，然后利用谱减关系计算增益因子g(k,i)，它们的表达式分别为：

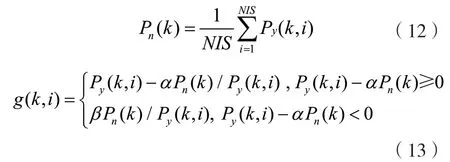
（6）计算谱减幅值，进行逆快速傅里叶变换（Inverse Fast Fourier Transform，IFFT）得到增强后的语音信号，计算流程为：

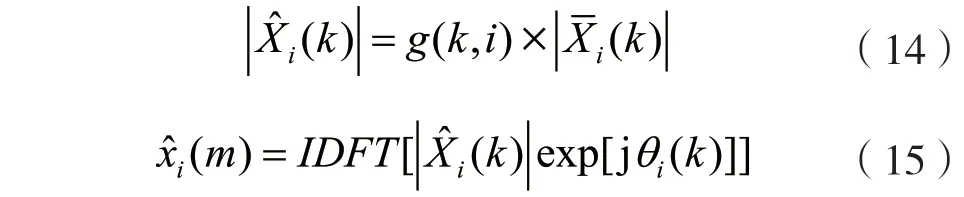
图1 多窗谱估计改进谱减法流程

2.2 NLMS 自适应滤波

自适应滤波器无须知道信号与噪声的先验统计知识，就能在工作中学习估计信号的统计特性，并依此调整参数，在某种准则下达到最优滤波[13-14]。因此，自适应滤波是处理非平稳信号的一种有效手段。在一般的自适应滤波算法模型中，假设语音信号观测模型为：

式中：d(n)为纯净语音；v(n)为噪声；x(n)为带噪语音。

维纳滤波器基于语音和噪声信号是联合宽平稳假设[15-16]，但语音一般非平稳，因此维纳滤波器的权系数是时变的，期望输出的估计值为观测语音信号的加权：

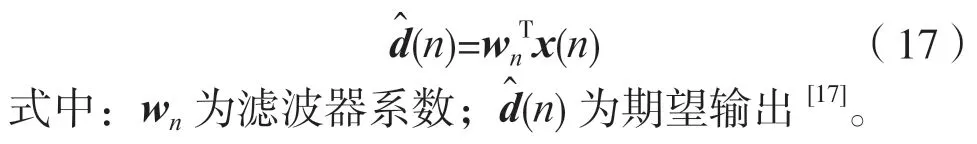
自适应滤波器不要求在每一时刻都使均方误差最小，而是对wn进行修正，修正过程为：

式中：Δwn为wn的修正值，误差信号为纯净语音与滤波器输出的差值。

NLMS 自适应滤波器的结构如图2 所示，其中，e(n)为期望信号与输出信号之间的误差。

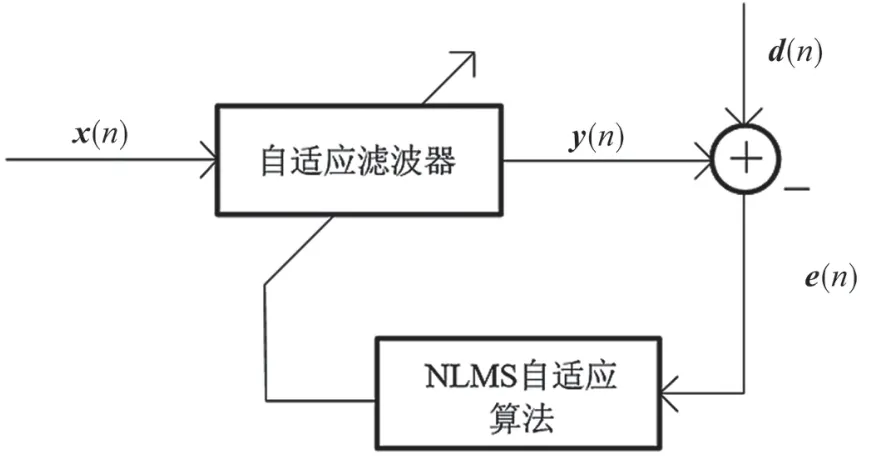
图2 NLMS 自适应滤波器结构

NLMS 即归一化LMS（Normalized LMS）算法，当抽头输入向量比较大的时候，LMS 会遇到梯度噪声放大的问题。为了解决这个问题，NLMS 算法使用抽头输入向量的平方欧式范数对抽头权值调整量进行了归一化[18]。

优化准则：

式中：J为优化准则函数；p为优化准则函数范数的次方项；w(k)为滤波器的第k个抽头系数。

为了防止分母为零，迭代方程需要添加修正因子α，修正步长μ调整的偏差。滤波器权系数更新如下：

式中：α为修正因子；e*(k)为误差项e(k)的复共轭，其中“*”表示复共轭。

NLMS 算法步骤：

（1）给定w(0)。

（2）计算输出值：y(k)=w(k)Tx(k)。

（3）计算估计误差：e(k)=d(k)-y(k)。

（4）权重更新：

MSS-NLMS 语音增强流程如图3 所示。将多窗谱估计谱减法和NLMS 自适应滤波算法相结合的一种算法为MSS-NLMS 算法。该算法首先使用多窗谱算法对带噪信号进行初步估计，在减少噪声的同时还可以弱化传统谱减法产生的“音乐噪声”；其次将估计出的期望信号与纯净参考信号的差值作为误差信号，由NLMS 算法代替传统的LMS 算法，求取滤波器权系数值，并不断迭代更新修正滤波器，以求取最优的滤波效果。

图3 MSS-NLMS 语音增强流程

3 算法仿真实验

3.1 实验方案

实验采用来自THCSH-30 语料库的纯音信号，噪声数据来源于NOISEX-92。实验在MATLAB 软件中进行仿真，采样频率fs=8 000 Hz，帧长25 ms，帧移10 ms。对一段纯净语音分别加入4 种典型噪声，分别是白噪声（White）、餐厅噪声（Babble）、机械噪声（Destroyerops）、工厂噪声（Factroy），并在不同的信噪比下，用本文MSS-NLMS 算法及各类谱减法进行对比实验。首先采用语音输入输出波形图及语谱图直观展示增强效果，从中可以清晰地看到增强后的语音还原程度；其次从语音质量指标PESQ 及语音可懂度评价指标STOI 出发，采用折线图的形式展现增强效果。

3.2 实验结果及分析

实验输出的波形及语谱如图4 和图5 所示。图4 是在0 dB 信噪比White 下，MSS-NLMS 和各类传统谱减对比结果。图5 是同一段语音在0 dB 信噪比Babble 下的结果。

图4 0 dB 信噪比White 下语音增强波形及语谱

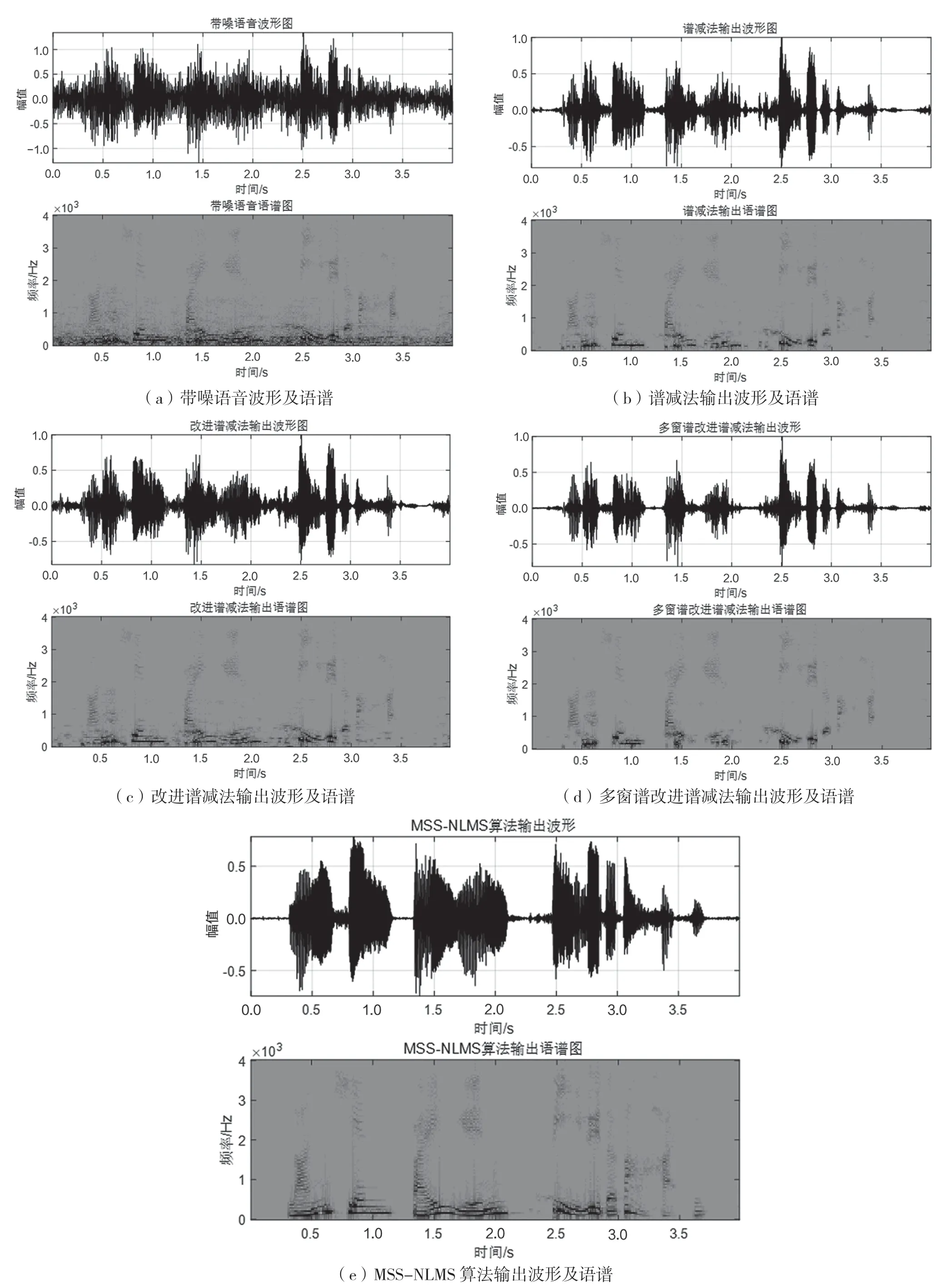
图5 0 dB 信噪比Babble 下语音增强波形及语谱

实验显示，谱减法提高了语音的质量，但图中仍然存在大量离散的噪声点，这是由于噪声功率谱之间的差异而产生的频谱尖峰即“音乐噪声”，会导致语音可懂度降低。在有色噪声Babble 和White下，谱减法及其改进方法都会选择牺牲可懂度或者语音质量其中一方，来换取另一方的提高，因此效果并不理想。虽然多窗谱改进法略优于以上两种方法，但也存在部分语音难以听清的情况，而可懂度较低难免会损失重要语音段。因此，本文在多窗谱改进法的基础上采用NLMS 算法进行进一步的滤波处理，将多窗谱改进后输出的语音信号送入NLMS自适应滤波器。如图4、图5 所示，相比于原始纯音信号，MSS-NLMS 算法输出的语谱图在语音存在较多的低频部分，且语谱中各频率分量复原程度较好，即增强效果较好。本文改进后的MSS-NLMS 算法在波形及语谱图上显示的增强效果明显优于其余3 种算法，说明本文所提方法不仅在低频区域取得了较好的处理效果，而且在较高的频率点处也有不错的效果。

图4、图5 仅给出了在两种噪声及0 dB 的低信噪比下的实验效果，更全面的实验结果如图6、图7 所示。

图6 4 种噪声下算法的PESQ 值

图6、图7 是在White、Babble、Destoryerops、Factory4 种典型噪声的场景下，语音质量指标PESQ值（0～5）和语音可懂度指标STOI 值（0～1）随着信噪比（SNR）变化的对比图。由图可知，在低信噪比（0～10 dB）下，本文改进算法有明显优势，滤波后语音质量及可懂度显著提高，即语音增强效果显著。

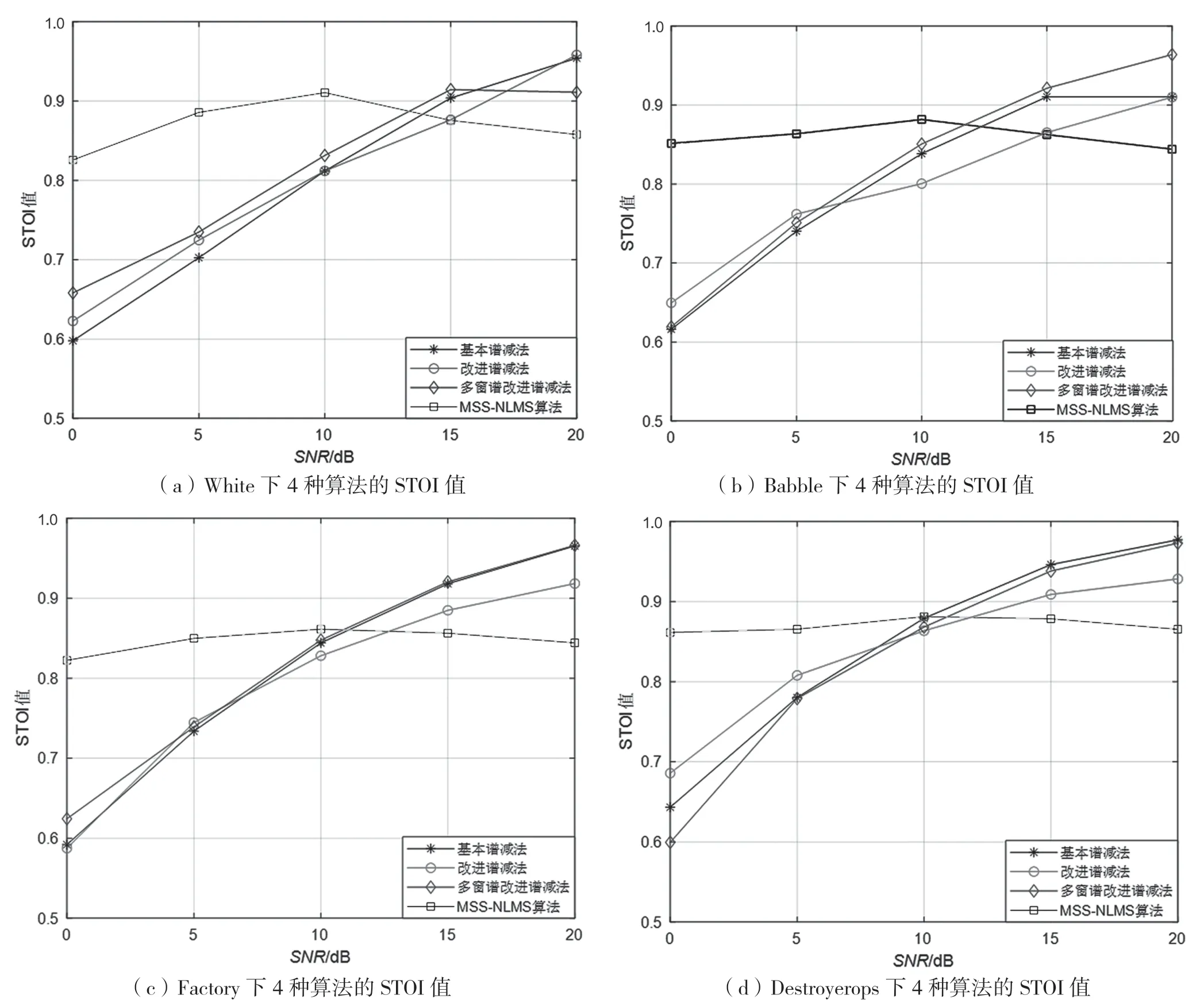
图7 4 种噪声下算法的STOI 值

综合比较，相比于其他方法，本文算法在0 dB下PESQ 值提升约为1.3，STOI 值提升约为0.23，但随着信噪比的提高，提升值也在逐渐减小，尤其在信噪比较高的情况（高于15 dB）下效果普遍降低，甚至不如传统的各类谱减法。据图初步分析，这是由于经过多窗谱输出后，语音质量及可懂度已经较好，再经过NLMS 滤波时，其步长因子没有做出相应调整，导致算法收敛精度下降，估计出现偏差，将一些恢复较好的语音成分给破坏掉了，最终导致增强效果减退。

综上，相比其他谱减法，无论在白噪声还是各种有色噪声下，本文MSS-NLMS 算法在低信噪比情况下语音增强效果提高明显，但信噪比偏高时效果略微降低。

4 结语

本文将多窗谱估计谱减法与自适应滤波的归一化最小均方算法联合应用到语音增强中，即先利用多窗谱法解决谱减法产生的“音乐噪声”问题，再将估计出的期望信号与纯净参考信号的差值作为误差信号，更新修正滤波器。在不同噪声、不同信噪比下进行对比实验，结果表明本文的MSS-NLMS 算法在强噪声环境（低信噪比）下增强效果明显优于各类谱减法。后续将在此基础上，增加对较高信噪比下增强效果退化的研究，并为基于传统信号处理及深度学习相结合的语音增强研究做准备。