二阶线性齐次常微分方程与方程组求解的类比法

张启峰， 徐定华， 徐映红

(浙江理工大学 理学院 数学系, 杭州 310018)

1 引 言

常微分方程是大学本科阶段理工科学生的必修内容，对于打算进一步从事工程和科学研究起着重要的桥梁和纽带作用.常微分方程也是数学专业核心课程如数学分析、高等代数等在微分方程这一分支方向的重要应用，同时也是后续学习偏微分方程的基础课程，因而在大学教学中有必要着重对待.

类比法是一类十分重要的认知手段和学习方法，是创新思维培养的基本方法[1-2].“它具有多种多样的形式，如低维与高维类比、离散与连续类比、有限与无限类比、微分与积分类比”[3]等等.具体的类比法案例包括函数与函数的类比[3]、积分变量的变换公式间的类比[4]、向量组线性无关性和函数线性无关性的类比[5]、阶乘函数推导的类比[6]、黎曼积分与勒贝格积分的类比、实数集与抽象集合的类比、欧几里得空间与Hilbert空间的类比等等.

本文将以二阶线性齐次常微分方程

(1)

和常微分方程组

(2)

为模型问题展示类比法.(1)中a为任意实数(分为a>0,a=0和a<0三种情形)，(2)中矩阵A∈n×n为对称正定矩阵或者零矩阵或者对称负定矩阵.设A=PTΛP，当A正定时，定义其中是以A特征根正的平方根为对角元素构成的对角矩阵；当A为负定时，定义是以-A特征根正的平方根为对角元素构成的对角矩阵.

二阶常微分方程具有广泛的应用，是高阶微分方程的典型代表，属于大学本科常微分方程课程的必修内容.本文通过二阶线性齐次常微分方程的求解类比及其数学论证，展示类比法的强大活力，为大学生的数学学习素材提供了更为丰富的类比法教学案例，有助于提升其创新能力.

2 特征函数法与降阶法的类比

2.1 特征函数法及其类比

首先利用教材中(例见文献[7]或[8])经典的特征函数法对(1)进行求解.令u(t)=eλt并将其代入到(1)的第一式，可得特征方程

λ2+a=0.

(3)

结合初始条件可得定解问题(1)的解为

(4)

(ii)当a=0时，方程(3)的解为λ=0(二重根).问题(1)的通解为

u=c1+c2t.

结合初始条件可得定解问题(1)的解为

u(t)=v+wt.

(5)

结合初始条件可得定解问题(1)的解为

(6)

基于类比的思想，猜测常微分方程组(2)的解分别如下：

(i)当A为对称正定矩阵时，类比(4)，问题(2)的解为

(7)

(ii)当A为零矩阵时，类比(5)，问题(2)的解为

(8)

(iii)当A为对称负定矩阵时，类比(6)，问题(2)的解为

(9)

2.2 降阶法及其类比

降阶法的基本思路是将原常微分方程(1)改写成一阶的常微分方程组，再利用一阶常微分方程组的相关理论获得其解的过程.

令U=(u(t),u′(t))T，则问题(1)等价于

其中

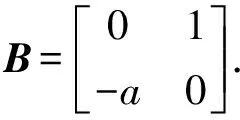
基于一阶线性常微分方程的分离变量法可知

U(t)=exp(Bt)U(0).

利用类比的思想，试猜测常微分方程组(2)的解为

(10)

其中

I为单位矩阵.

上述两组形式解：解(7)-(9)与解(10)是否一致，下节将论证之.

3 类比法中解的等价

由第2节分别获得了常微分方程(1)的两种不同形式的解.并用类比的思想给出了常微分方程组(2)的两种形式的解.容易验证(7)-(9)与(10)均为(2)的解.下面直接证明形式解(7)-(9)与(10)的等价性.

为简洁起见，本文仅给出当矩阵A为正定矩阵时，(2)的解(7)等价于(10).感兴趣的读者可以尝试当矩阵A为零矩阵,(8)与(10)等价；当矩阵A为负定矩阵，(9)与(10)等价.

为说明(7)与(10)的等价性，首先给出矩阵的欧拉公式.

引理1设A为正定矩阵，则有

定理1当矩阵A为正定矩阵时，(7)等价于(10).

证利用指数函数的泰勒公式，(10)可转化为

(i)当n为偶数时，即n=2k时，

(ii)当n为奇数时，即n=2k+1时，

因而

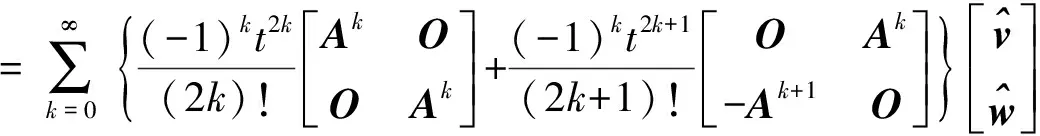
另一方面，由(7)可知

上式结合解(7)可得

接下来，将确认上式中的各个分量aij(i,j=1,2)和矩阵(11)中的右端分量是一致的.易知a22=a11，因而仅需验证a11，a12，a21和(11)右端矩阵的分量对应相同.利用引理 1可得

结合论证，可知(7)与(10)等价.

4 结 论

大学中教学创新[9]有多种多样，包括教学模式创新、教学方法创新、教学内容创新、学习方法创新等等.本文属于教学内容与教学方法创新，对常微分方程和方程组利用两种方法求解，对解的形式进行大胆猜测，数学上给出严格验证，实现了学习方法和内容剖析的统一.

本文是类比法在二阶线性齐次常微分方程求解中的一个成功案例.在大学数学中还有很多数学思想与方法都值得研究，如归纳法、反证法、常数变易法、可视化教学法[10]等等.本文的研究有助于培养学生创造性思维.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.感谢浙江理工大学程秀俊博士有益的讨论.