基于映射弹性势能增量的电网主振荡路径识别

路广才，竺 炜，唐颖杰

(1.长沙理工大学电气与信息工程学院，湖南 长沙 410114；2.国网青海省电力公司西宁供电公司，青海 西宁 810000)

近年来，实际电网时常发生范围广、周期长的低频振荡现象，危及电网的安全稳定运行[1-3]。现有研究低频振荡的机理主要有负阻尼机理和强迫功率振荡机理[4-5]，其中，负阻尼机理难以解释由电网边界(电源及负荷侧)波动引起的低频振荡现象，但是强迫功率振荡机理可以给出较好解释，因此，许多学者对强迫功率振荡问题开展了大量研究。强迫功率振荡主要是由发电机侧扰动引起的[5]，而文献[6-8]通过深入研究电网及负荷侧扰动引起强迫功率振荡的问题，进一步完善了强迫功率振荡机理；为了便于直观感受电网状态量的变化趋势以及增强对电网的物理理解，文献[9]提出了电网—弹性力学网的拓扑映射理论，该理论现主要用以分析静态功角稳定问题，尚未应用于分析电网动态稳定性；在此基础上，文献[10]从负荷侧扰动引起强迫功率振荡的角度出发，通过映射弹性力学网研究功率振荡特征，验证了以力学视角分析电网功率振荡是可行的。

当电网发生功率振荡时，准确找寻到扰动源位置并及时切除扰动源或采取控制措施，是抑制振荡的常用方式。针对扰动源位置的辨识问题，学者们提出了诸多振荡扰动源的定位方法[11-13]，并且已取得良好成效。然而，振荡过程必然存在一系列交互通道(振荡路径)，其中存在某一振荡路径下的若干线路振荡最剧烈，该路径即为主导振荡路径。如果能找到主导的振荡路径并采取有效防治措施，便能更好地抑制低频振荡现象，有助于电网的安全稳定运行。目前，鲜有学者研究电力系统低频振荡路径的辨识问题。文献[14]从能量角度分析了电力系统振荡过程中网络暂态能量的变化规律，文中定义承担暂态能量最大的支路为主振荡支路；文献[15-16]证实了区间振荡模式下主振荡路径的存在，并利用网络状态量(电压、电流及相角)的灵敏度与发电机振型的关系辨识主振荡路径。

在前期研究基础上[9-10,17-18]，基于电力系统与弹性力学系统的映射关系，本文将电网映射成弹性力学网，构建含阻尼特性的映射弹性力学动态模型，仿真发现二者动态特性基本一致，验证其动态映射的合理性。根据受迫振动的能量转换机理[19]，分析电力系统功率振荡过程中系统能量的转换特性，在此基础上，通过建立辨识主振荡路径的指标获得全网主振荡路径，算例分析验证所提方法的有效性。

1 电力系统的映射弹性力学动态模型

1.1 发电机的映射弹性力学模型

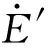
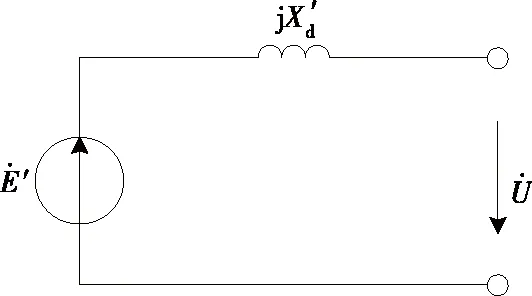
图1 发电机等值电路Figure 1 Equivalent circuit of generator

(1)

式中TJ为发电机惯性时间常数；Pm、Pe分别为机械功率和电磁功率；Δω为转子角速度偏差；Δδ为转子角偏差；D为阻尼系数。

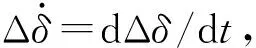
(2)

弹性力学系统的单自由度质—阻—弹力学模型由质量块、阻尼器、弹簧等理想元件构成，如图2所示。

图2 单自由度质—阻—弹模型Figure 2 Mass-damper-spring model with single degree of freedom

无外扰力作用时系统处于静平衡(稳定)状态。令Δx为位移，以质量块的静平衡位置为坐标原点建立坐标轴。根据牛顿第二定律可知，该模型受到小扰动后的运动微分方程为

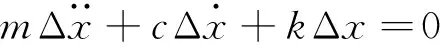
(3)

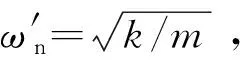
以上分析发现，2个不同系统的动力学方程及固有特性参数具有高度相似性，动态本征一致。再对比式(1)、(3)，可得映射关系：

(4)

1.2 映射弹性力学动态模型的构建

设交流支路Lij的两端电压为Ui、Uj，相角差为θij，线路电抗为Xij，忽略电阻，则该线路传输的有功功率为

(5)

对式(5)线性化近似可得：

(6)

根据文献[17]，线路的有功—相角特性与弹簧的受力—形变特性类似，故可将电网线路映射为单自由度弹簧，状态量的映射关系为

(7)

式中F、x分别为弹簧的作用力和形变量；弹性系数k=dF/dx，则Kij为支路Lij的映射弹性系数。

文献[9]将电网侧网络结构映射成弹性力学网，而根据对发电机及单自由度质—阻—弹模型的动态特性分析，可将发电机侧映射至弹性力学网，进一步完善电网—弹性力学网的映射理论。

根据式(4)、(7)的映射关系可将整个电力系统映射成弹性力学系统，即电网映射成一个二维平面的纵向弹性力学网。如图3所示，电网中的发电机映射为集中质量块，机械阻尼映射为同质量块相连的阻尼器，发电机支路和电网线路映射为弹簧，有功负荷映射为向下的外施作用力，网络拓扑的映射参见文献[9]。

图3 电网拓扑映射Figure 3 Power grid topology mapping

因此，电力系统的映射多自由度弹性力学模型的运动微分方程为

i=1,2,…,m

(8)

式(8)化为矩阵形式为

(9)

式中M=diag[TJ1/ω0,TJ2/ω0,…,TJm/ω0]为质量矩阵；K为刚度矩阵，具体求解见文献[10]；C=diag[D1/ω0,D2/ω0,…,Dm/ω0]为阻尼矩阵。

对式(9)所表征的相应无阻尼系统(C=0)进行固有振动分析，求出各阶固有振动频率ωi及相应振型φi，获取其谱矩阵Λ及振型(模态)矩阵Φ。则系统的主质量、主刚度和主阻尼矩阵为

(10)

2 功率振荡的能量转换特性

类比于弹性力学受迫振动过程中的能量转换特性[19]，将电网映射为弹性力学网后，根据受迫振动的能量转换原理，对电网功率振荡过程的能量特性进行剖析。以单机无穷大系统为例，系统在工作点处的线性化运动方程同式(1)。假设发电机机械功率发生扰动，其变化量为ΔPm=P0sin(ωt+β)，则式(1)可改写为

(11)

式(11)即为电网的映射弹性力学网中发电机的受力平衡式，等式左边表征加速力和弹性恢复力之和，右边表征外扰力和阻尼力之差。若系统的发电机转子角偏差(位移)响应为Δδ(t)=Hsin(ωt+β)，则等式两边同对Δδ积分，可得系统的能量平衡方程为

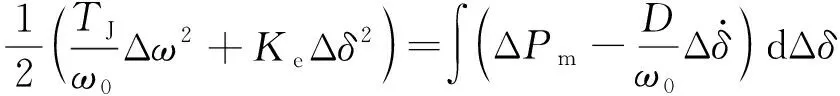
ΔWk(t)+ΔWp(t)=W(t)

(12)

式中W(t)为功率扰动输入能量与阻尼耗能的差值，即系统振荡时的净输入能量函数；ΔWk(t)、ΔWp(t)分别为系统的动能增量函数和势能增量函数，其表达式为

考虑在一个振荡周期内的能量增量，有

(13)

可知在一个振荡周期内，无论系统动能增量ΔWk与系统势能增量ΔWp相等与否，系统的净输入能量W均为恒定值。如图4所示，当系统处于稳态振荡时，系统动能和势能可以相互转换，二者此消彼长，系统保持周期性能量平衡，振荡形式综合表现为无阻尼自由振荡。

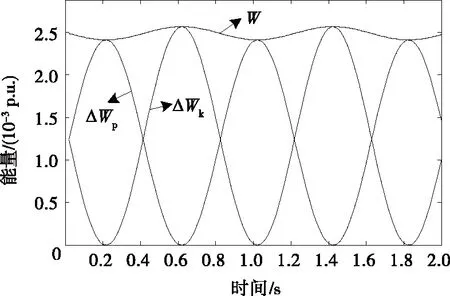
图4 能量转换特性Figure 4 Energy conversion characteristics

对于多机电力系统，若系统有m台发电机、n个节点，系统在受到周期性功率扰动后，将发电机的动能及支路势能分别加和，得到其动能增量函数和势能增量函数为

(14)

则总的净输入能量增量函数为

W(t)=ΔWk(t)+ΔWp(t)

(15)

系统各节点有功功率平衡方程为

(16)

式中Pdi为节点i有功负荷；Pij为支路Lij的有功功率。

式(16)线性化方程为

(17)

取Δφ=[ΔδT,ΔθT]为系统所有节点相角偏差，则系统势能增量函数又可表示为

(18)

系统功率振荡在一个周期内的总能量保持不变，且总能量是由发电机转子动能与发电机支路势能共同组成，两者相互转换。根据式(18)可知，发电机支路势能经由与其相连支路将势能在网络中传播，并存储在各个支路，则系统总的势能为各支路势能累加值。

由式(6)、(18)可得：

(19)

由于式(19)是基于电网模型与弹性力学模型的映射关系推导而得，且与文献[18]进行区分，故本文定义其为支路映射弹性势能增量函数(简称势能增量函数)。

3 电网主振荡路径的辨识方法

3.1 路径振荡指标

通过前述将电网映射为弹性力学网，再依据弹性力学的功能原理以分析相应电网功率振荡的能量转换特性，即功率振荡过程伴随着能量的交互传递(系统动能和势能之间的转换)。由各支路组成的电力网络是能量交互的媒介，支路就是能量传递的通道，而外扰力(功率扰动)做功产生向系统输入的外界能量以势能形式流向网络并存储在各支路中。

能量是一个物理概念，在分析振荡(或振动)问题中具有重要作用，振荡过程存在能量的转化和传递[20]。系统受扰后的外界输入能量可用以表征系统振荡程度，能量越大振荡越剧烈。因此，某一支路的振荡程度可用一个振荡周期内的平均势能增量衡量，即

(20)

以扰动源为始点、发电机为终点(若扰动源为发电机，则另一发电机为终点)，经过若干节点并依次添加相关线路，直至连接成一条连通路径，此路径即为一条振荡路径。

本文将所有经过某一路径的有关支路表征的WL的累加值定义为该路径的振荡指标：

(21)

电网的振荡路径多而不一，不同路径的振荡程度亦不同。以存储能量大(振荡程度最剧烈)的路径视为主振荡路径，则经式(21)求得WR值最大的路径即为主振荡路径。

3.2 Floyd算法

Floyd算法是一种求取任意两点之间最短路径的经典算法，通过一个拓扑图的权值矩阵求出它的任意两点间的最短路径，可以正确解决无向图、有向图或负权的最短路径问题[21]。

对于赋权无向图G(V,W)，以V={v1,v2,…,vn}表示拓扑网络图的顶点集合，W=(ωij)n×n为G的邻接矩阵，矩阵元素ωij为边(vi,vj)的权值，若顶点vi、vj之间无邻边，则ωij=∞。任意2个顶点vi、vj之间的最短路径有2种可能：①直接从vi到vj；②从vi到vj之间经过若干节点。

用dij表示顶点vi、vj之间的最短距离，对于任意节点vk，若满足dij>dik+dkj，则令dij=dik+dkj，遍历每个节点，更新n次后，计算完成。用rij表示经过顶点vi、vj之间的点集，rij随着dij同时更新，则R=(rij)n×n为最短路径矩阵，D=(dij)n×n为最短距离矩阵。

图G有n个顶点，计算最短距离矩阵D和最短路径矩阵R需要进行n次更新。具体步骤如下。

1)赋初值。

2)对顶点vk∈V更新矩阵。

更新计算为

(22)

3)获得矩阵D、R。

3.3 主振荡路径的辨识

电力系统单从其接线拓扑图来看是一个无向图G(V,W)，其邻接矩阵W可用来描述电力系统的网络结构。基于上述所建立的衡量支路Lij振荡程度的指标WLij，对图G相关边W(i,j)赋权为1/WLij，则某一路径距离dij越小，WR值越大，那么电网主振荡路径的辨识问题就转变为最短路径的求解。通过利用Floyd算法可以快速确定主振荡路径，主振荡路径辨识的具体步骤如下：

1)量测电网各支路有功功率值、各节点电压值及相位值；2)获取各支路Lij有功功率变化量ΔPij、相位差变化量Δθij，根据式(20)，计算支路Lij的平均势能增量WLij；3)设WLij为支路Lij的权值，则邻接矩阵W(i,j)=1/WLij，并对矩阵D、R赋初值；4)根据式(22)更新计算dij、rij，获取矩阵D、R；5)根据步骤4)结果，通过矩阵D、R追溯获得任意两节点间的最短路径及其距离，该连通路径即为电网主振荡路径。

4 算例分析

4.1 电网动态映射的合理性验证

以IEEE 9节点系统为例，发电机采用经典二阶模型，系统结构可见图3(a)。根据前文所述方法，将IEEE 9节点系统映射成弹性力学网(图3(b))，计算得到映射弹性力学网各弹簧支路的刚度系数，获取式(10)相关矩阵，得到系统振荡模式的相关信息，如表1所示。IEEE 9节点系统小干扰稳定分析计算结果如表2所示。

表1 映射弹性力学网特征值计算结果Table 1 Calculation results of eigenvalues of mapped elastic networks

表2 IEEE 9节点系统小干扰稳定结果Table 2 Small signal stability results of IEEE 9-bus system

以振荡模式1为例，设电网节点6处的负荷发生周期性小扰动引发强迫功率振荡；同样类比电网负荷扰动情形，在弹性力学网联络节点6处施加相同激振力，扰动时间为0～5 s，则系统发电机有功出力的波动曲线如图5所示，质量块受力变化曲线如图6所示。

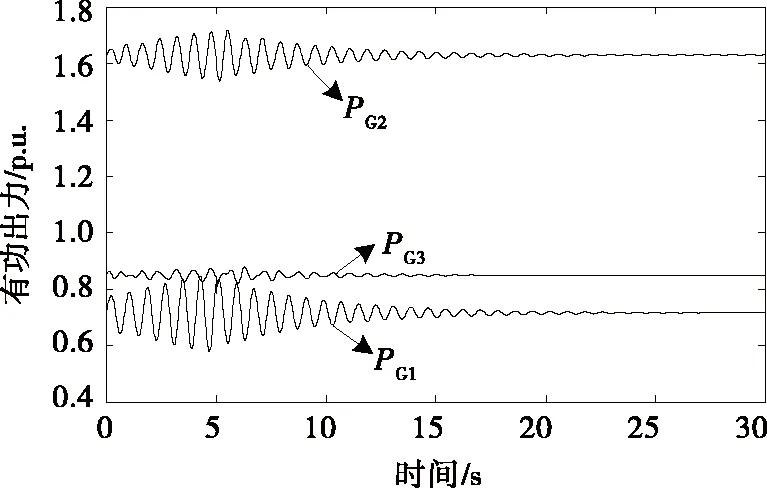
图5 发电机有功出力的波动曲线Figure 5 Fluctuation curve of generator active power output

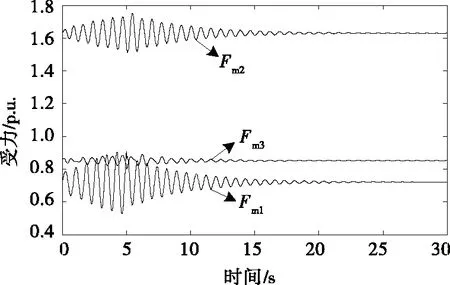
图6 质量块受力变化曲线Figure 6 Force variation curve of mass

对比图5、6可以看出，发电机有功出力的波动曲线与质量块受力变化曲线近乎同等。再对比表1、2结果发现，电力系统与映射弹性力学系统的振荡模式基本相同，二者振荡频率及阻尼比非常相近，说明其动态特性具有一致性。因此，电力系统的映射弹性力学动态模型可以较准确地反映电网的振荡特性，进而验证二者动态映射的合理可行。

选取振荡稳态时段的部分数据，计算功率振荡的能量变化，其趋势如图7所示，系统一个振荡周期的能量增量如表3所示。

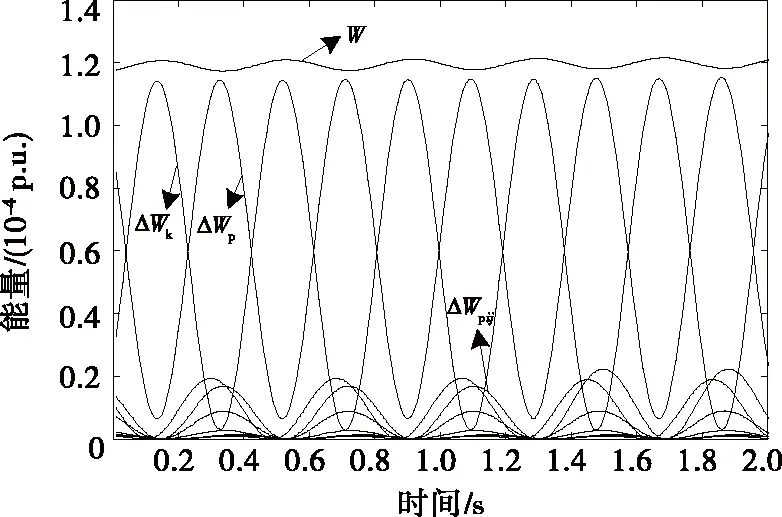
图7 能量变化趋势Figure 7 Energy change trend

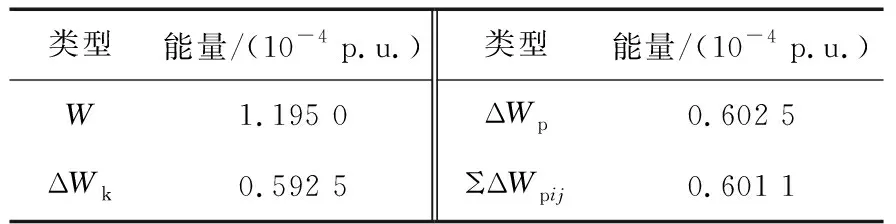
表3 一个振荡周期的能量增量Table 3 Energy increment of an oscillation period

从图7可以看出，当电力系统振荡稳态时，系统总能量W、动能增量ΔWk、势能增量ΔWp均随时间波动。由表3可知，一个振荡周期内的动能增量与势能增量虽不相等，但系统总能量是恒定的，其中势能增量ΔWp与各支路势能增量累加值ΣΔWpij基本相等。该仿真结果与前述分析结论一致。

4.2 电网主振荡路径的确定

以IEEE 39节点系统为例，根据2个振荡模式(如表4所示)，本文分别从机械、负荷功率周期性扰动2种情形进行分析，确定电网的主振荡路径。扰动幅值均设为0.7 p.u.，扰动时间为0～5 s。

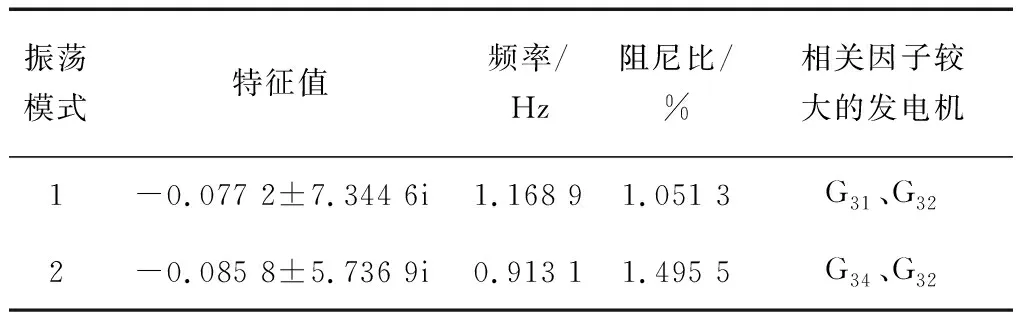
表4 IEEE 39节点系统小干扰稳定结果Table 4 Small signal stability results of IEEE 39-bus system

1)机械功率周期性扰动。

以振荡模式1为例，假设发电机G31为扰动源，存在周期性机械功率扰动引发系统强迫功率振荡。在振荡稳态阶段，取部分时段数据进行支路势能增量函数的计算。系统支路势能增量波动趋势如图8所示，振荡路径的WR计算结果如表5所示。

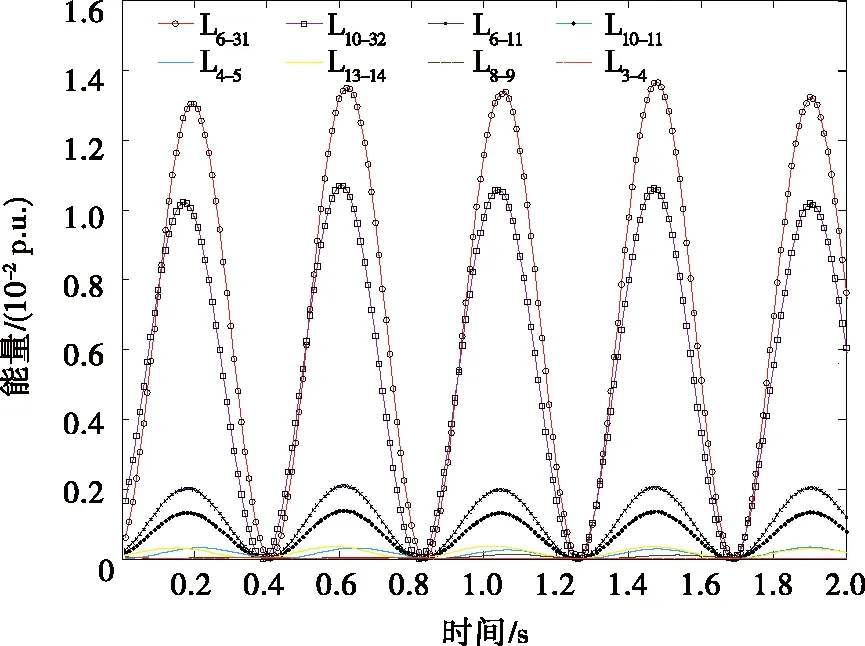
图8 支路势能增量变化曲线Figure 8 Variation curve of branch potential energy increment

以支路10-11、4-14为例，其支路势能增量平均值分别为0.071、0.012。如图9所示，对比2个支路的势能增量平均值与有功功率波动发现，支路10-11功率波动程度较支路4-14明显，说明支路势能增量平均值衡量其振荡程度是合理的。

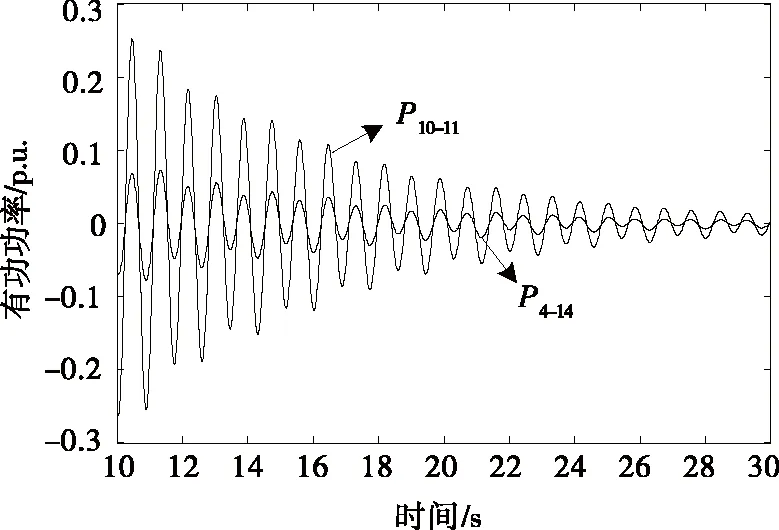
图9 有功功率波动曲线Figure 9 Active power fluctuation curve

根据表5振荡路径的WR计算结果，可知路径R{31,6,11,10,32}的d值最小，WR值最大。以扰动源发电机G31为起始点，依次添加支路6-31、6-11、10-11和10-32连接至发电机G32，形成一个连通路径，如图10所示，该路径即为电网主振荡路径。比较系统各支路势能增量变化，从图8可以看出，支路6-31、10-32的势能增量变化显著，说明G31、G32振荡较剧烈。同时，G31、G32也是该振荡模式下相关因子较大的机组，侧面说明G31、G32间相关支路作为主振荡路径是合理的。

图10 电网主振荡路径Figure 10 Main oscillation path of a power grid

2)负荷功率周期性扰动。

以振荡模式2为例，设节点18处负荷功率发生周期性扰动，进而导致系统发生功率振荡。取振荡稳态时段的部分数据计算系统各支路势能增量函数，其变化趋势如图11所示，振荡路径的WR计算结果如表6所示。

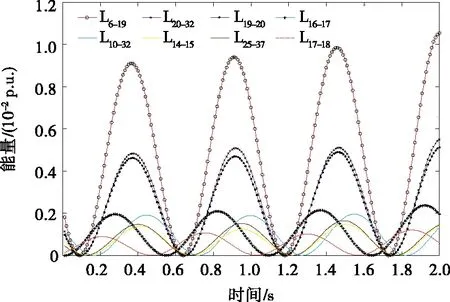
图11 支路势能增量变化曲线Figure 11 Variation curve of branch potential energy increment

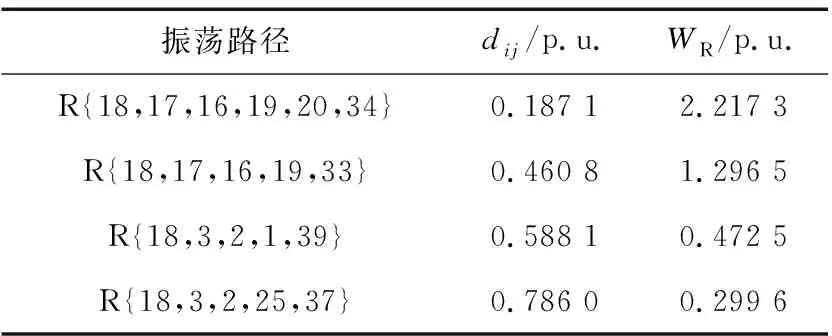
表6 振荡路径WR计算结果Table 6 WR calculation results of oscillation paths

由图11可知，发电机出口支路20-34势能增量变化明显，发电机G34振荡剧烈。同理，根据表6结果，路径R{18,17,16,19,20,34}的d值最小，WR值最大，故连接扰动源节点18至发电机G34的相关线路为一个连通路径。该连通路径见图10，即为主振荡路径。

5 结语

通过对电力系统与弹性力学系统的相似性分析，发现二者在基本组成结构与数学模型上均具有高度相似性，从而得到两不同系统的映射关系，构建了电力系统的映射弹性力学动态模型。算例和分析均表明，2个不同系统的动态特性十分契合。

将电网映射成弹性力学网，系统受扰后可以通过弹性力学网的“伸缩”直观感知电网的振荡区域，有助于清晰理解功率振荡的物理过程。从新的视角出发，可以借助力学方面的知识分析电网的低频振荡现象，拓新研究低频振荡的思路。

基于受迫振动的能量转换原理，分析了电力系统功率振荡时的能量转换特性，即稳态振荡时动能与势能增量周期性波动，但一个振荡周期内总能量保持恒定，系统保持周期能量平衡；揭示了电网功率振荡时的能量交互规律，即功率扰动产生的外界输入能量是以势能形式在网络中传递。在此基础上，利用建立的路径振荡指标辨识电网的主振荡路径，可以有效识别出电网的振荡区域，为研究开展相应抑制低频振荡措施提供实际参考价值。