K*∀谓词逻辑系统中相似度及伪距离研究

鲁星，惠小静，王波

（延安大学 数学与计算机科学学院，陕西 延安 716000）

模糊逻辑是由经典逻辑和多值逻辑推广而来的，在生活的各个领域中获得了广泛的应用。近几十年来，模糊逻辑得到了越来越多学者的关注。在模糊逻辑的发展历程中产生了多方面的研究成果［1-5］，三角模的模糊逻辑在模糊逻辑的形式化研究中占据主导地位。典型的基于三角模的模糊逻辑主要有基于幂零极小三角模L*逻辑［6-7］、基于连续三角模的BL逻辑、基于左连续三角模的MTL逻辑等。模糊逻辑在相似度、概率真度、Γ-真度、近似推理等方面取得了许多成果［9-17］。

基于连续三角模的K*逻辑系统是裴道武等于2002年提出的［6］，与K*逻辑系统相对应的谓词逻辑系统是L*。谓词逻辑系统K*∀是在命题逻辑系统L*的基础上，增加了带有全称量词和存在量词的逻辑，目前相似度和伪距离大都建立在命题逻辑系统中，在谓词逻辑系统中只有少数学者做出了一些研究。王国俊在命题系统中引入了公式真度的概念，将数理逻辑符号化、形式化的特征与数值计算相结合，提出了计量逻辑学［18］，进一步给出了相似度与伪距离的概念。

本文在文献［18］的基础上对谓词逻辑系统K*∀展开计量化研究。主要研究不含函数符号的一阶闭逻辑公式之集Φ中公式之间的相似度，给出了含有量词符号公式的相似度与真度的关系，同时研究了谓词逻辑系统K*∀中公式相似度和伪距离的性质及其计算方法，为进一步研究发散度与相容度奠定了基础。

1 预备知识

1.1 公理化真度

文献［18］基于有限模型和均匀概率的思想对非单调逻辑中的典型案例做了分析，通过概率计算给出了应当赋予文字的完全闭包及其合取的真度值。以此为基础，本文在Ф中建立了公理化的真度理论。Ф是全体不含函数符号的一阶闭逻辑公式之集，用A，B，C等表示Ф中的一阶逻辑公式。下面首先对Ф中公式真度的定义和真度映射τ具有的性质进行说明。

定义1.1［18］称映射τ：Ф→[0，1]为公理化真度映射，若以下条件成立：

（K1）不出现相同谓词符号的N个文字的完全闭包的合取的真度等于；

（K2）若A是Ф中的定理，则τ(A)=1；

（K3）τ(¬A)=1-τ(A)，A∈Ф；

（K4）τ(A→B)+τ(A)=τ(B→A)+τ(B)，A，B∈Ф；

（K5）τ(cl(¬Q))=1-τ(clQ)；

（K6）在计算公式的真度时，其中原子公式中的变元可以相互替换。

当A∈Ф时，称τ(A)为A的公理化真度，简称为A的τ-真度或真度。

命题1.1［18］真度映射τ具有以下性质：

i）若A是矛盾式，则τ(A)=0；

ii）若A与B逻辑等价，则τ(A)=τ(B)；

iii）若τ(A→B)=1，则τ(A)≤τ(B)；

iv）若τ(A)≥a，τ(A→B)≥b，则

τ(B)≥a+b-1；

v）若τ(A→B)≥a，τ(B→C)≥b，则

τ(A→C)≥a+b-1；

vi）τ(A→C)≥τ(A→B)+τ(B→C)-1；

vii）τ(A∨B)+τ(A∧B)=τ(A)+τ(B)。

1.2 谓词逻辑系统K*∀的公理包含以下两类

本小节对谓词逻辑系统K*∀的语构理论及一阶逻辑的公理化真度进行说明。

定义1.2［5］K*∀中的公理集，其中A，B，C为谓词公式。

i）系统K*中的公理：

（K*14）(∀x)(A→B)→(A→(∀x)B)，x在B中不自由；

（K*15）(∀x)(A∨B)→((∀x)A∨B)，x在B中不自由。

ii）带有量词的公理：

（∀1）(∀x)A(x)→A(t)（在A(x)中可用t替代x）；

（∃1）A(t)→(∃x)A(x)（在A(x)中可用t替代x）；

（∀2）(∀x)(B→A)→(B→(∀x)A)（x在B中不自由）；

（∃2）(∀x)(A→B)→((∃x)A→B)（x在B中不自由）；

（∀3）(∀x)(A∨B)→((∀x)A∨B)（x在B中不自由）。

系统K*的推理规则有以下两条：

MP规则［5］：由A，A→B推出B；

推广规则［5］：由A推出(∀x)A。

命题1.2［5］在系统K*∀中，以下结论成立：

HS规则：A→B，B→C可得A→C；

交推理规则：A→B，A→C，可得A→B∧C。

命题1.3［18］设A，B，C∈Φ，则

i）ξ(A，B)=ξ(B，A)；

ii）若A与B逻辑等价，则ξ(A，B)=1；

iii）ξ(A，B)=τ(A→B)+(B→A)-1；

iv）ξ(A，B)=1+τ(A∧B)-τ(A∨B)；

v）ξ(A，B)+ξ(A，¬B)=1；

vi）ξ(A，B)+ξ(B，C)≤ξ(A，C)+1。

定义1.3［18］设A，B∈Φ，令

ρ(A，B)=1-ξ(A，B)，称ρ(A，B)为A与B之间的伪距离。

定义1.4［18］设A，B∈Φ，令

ξ(A，B)=τ((A→B)∧(B→A))，称ξ(A，B)为A与B之间的相似度。

命题1.4［18］设A，B，C∈Φ，则

i）ρ是Φ上的伪距离，但不是距离；

ii）ρ(A，B)+ρ(A，¬B)=1；

iii）ρ(A，B)=τ(A∨B)-τ(A∧B)。

命题1.5［5］以下公式是K*∀中的定理：

i）├(∃x)(A∧B)↔(A∧(∃x)B)；

ii）├(∀x)A→(∃x)A；

iii）├A∧B→B；

iv）├(∀x)(A→B)↔((∃x)B→A)。

2 相似度及伪距离运算性质的研究

定理2.1当x在B中不自由时，ξ(A，B→A∧B)=τ(A)-τ(B→A∧B)+1。

证明由定义1.2（K*6）知A→(B→A∧B)是定理。由定义1.1（K2）知τ(A→(B→A∧B))=1。

由命题1.3的ⅲ）可得

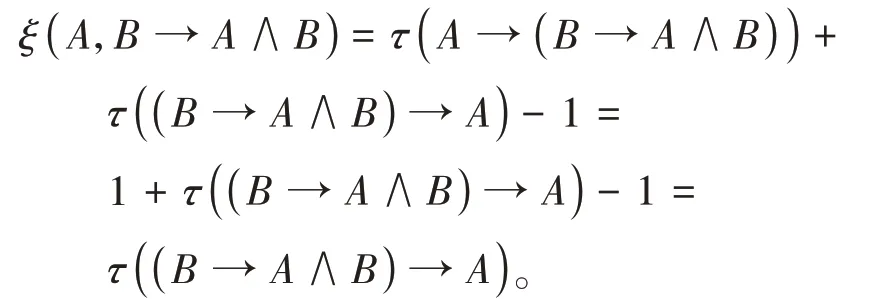
由定义1.1（K4）知

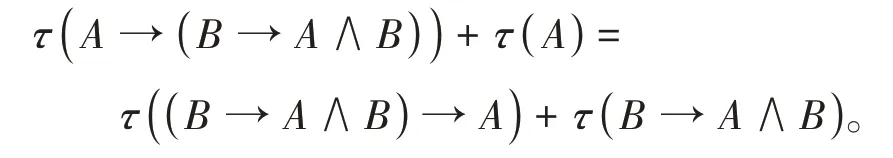
所以τ((B→A∧B)→A)=1+τ(A)-τ(B→A∧B)。

ξ(A，B→A∧B)=τ(A)-τ(B→A∧B)+1得证。

定理2.2当x在B中不自由时，ξ(A，(∃x)B)=2τ(A∧(∃x)B)。

证明由定义1.1（K1）知，所以。

由命题1.1的vii）和命题1.3的vii）知

即ξ(A，(∃x)B)=2τ(A∧(∃x)B)得证。

例2.1求ξ(A，(∃x)B)的值。

解由定理2.2知ξ(A，(∃x)B)=2τ(A∧(∃x)B)。

由命题1.5的i）知(∃x)(A∧B)↔A∧(∃x)B是定理，所以(∃x)(A∧B)→A∧(∃x)B和A∧(∃x)B→(∃x)(A∧B)都是定理，又根据定义1.1（K2）知

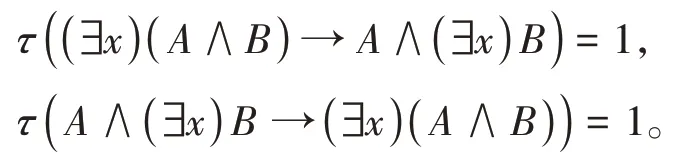
根据命题1.1的iii）知

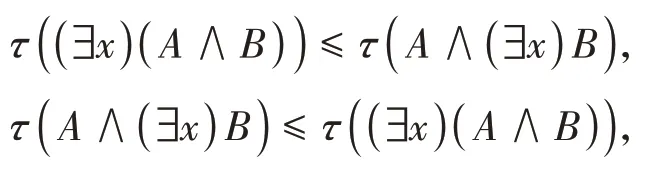
所以τ((∃x)(A∧B))=τ(A∧(∃x)B)。

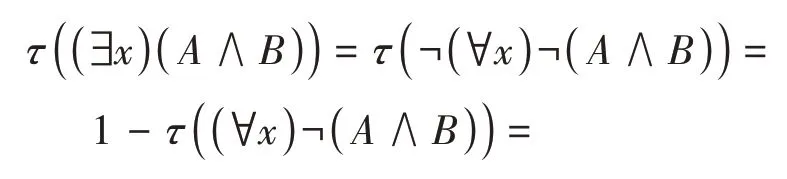
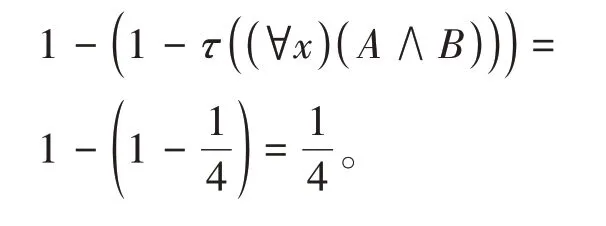
所以ξ(A，(∃x)B)=2τ(A∧(∃x)B)=。

定理2.3证明ξ(A∨B，B∨A)=τ(B∨A→A∨B)。

证明由定义1.2（K*7）知A∨B→B∨A是定理，由定义1.1（K2）知τ(A∨B→B∨A)=1，由命题1.3（iii）知

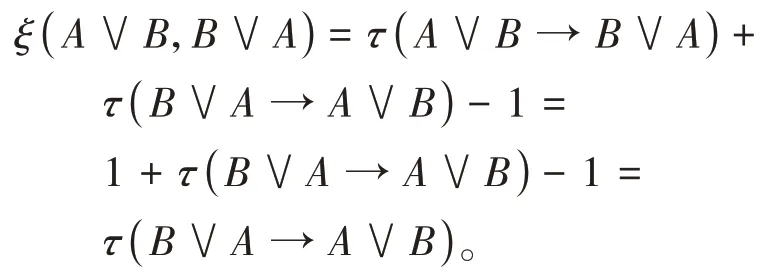
即ξ(A∨B，B∨A)=τ(B∨A→A∨B)得证。

定理2.4证明ξ((∃x)A，(∀x)A)=2τ((∃x)A∧。

证明由命题1.5的ii）知(∀x)A→(∃x)A是定理，由定义1.1（K2）知τ((∀x)A→(∃x)A)=1。

又由定义1.1（K1）知

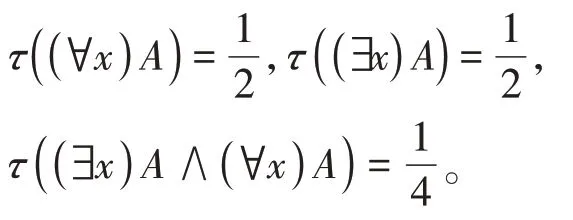
由命题1.3的iv）知

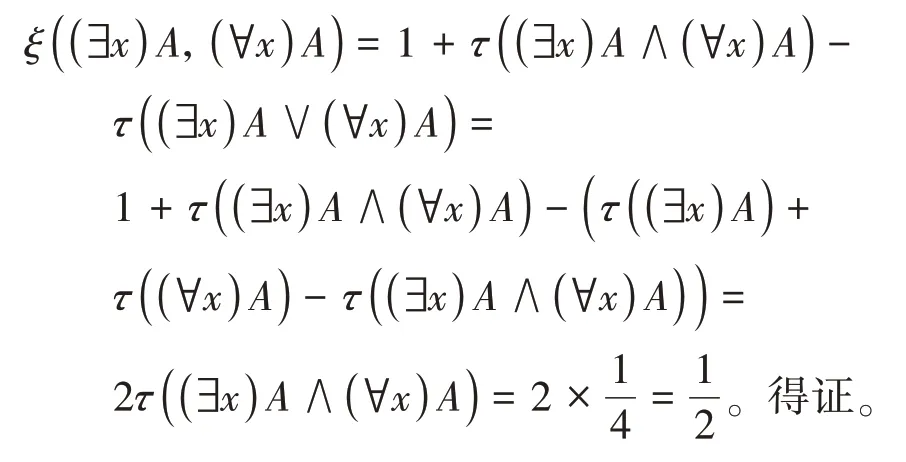
例2.2 求ξ(B→A∧B，¬A)，ρ((B→A∧B)，A)的值。

解由定义1.2（K*11）和命题1.5的iii）知A→(B→A∧B)，A∧B→B是定理，根据定义1.1（K2）知τ(A→(B→A∧B))=1，τ(A∧B→B)=1。

又由定义1.1（K1）知τ(A)。

由定义1.1（K4）知

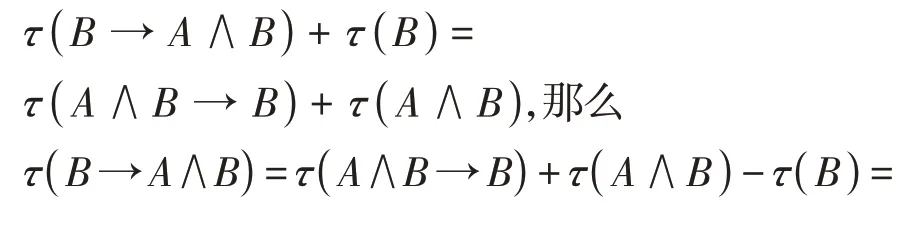
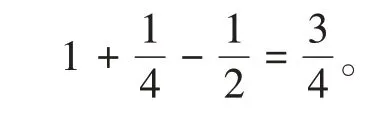
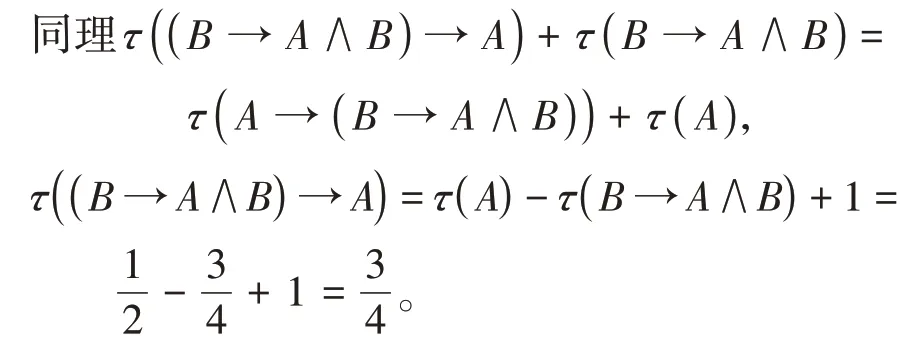
由命题1.3的iii）和命题1.3的v）知

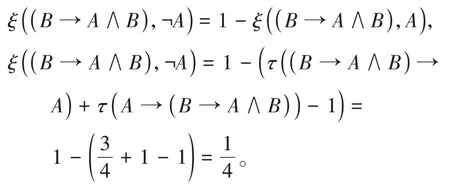
由定义1.3知ρ(A，B)=1-ξ(A，B)，那么

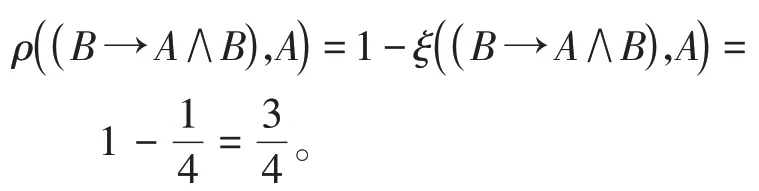
例2.3求ρ((∀x)(A→B)，¬((∃x)B→A))的值。

解由命题1.5的iv）知(∀x)(A→B)↔((∃x)B→A)是定理，所以(∀x)(A→B)→((∃x)B→A)，((∃x)B→A)→(∀x)(A→B)都是定理，由定义1.1（K2）知τ((∀x)(A→B)→((∃x)B→A))=1，

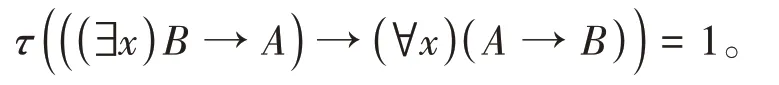
又由命题1.4的ii）知ρ(A，¬B)=1-ρ(A，B)，由命题1.3的iii）和定义1.3可知ρ(A，B)=1-ξ(A，B)，那么

定理2.5证明。

证明由定义1.2（K*1）知A→(B→A)是定理，

由定义1.1（K1）和（K2）知τ(A→(B→A))=1，

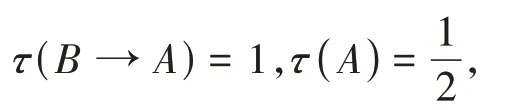
由命题1.3的iii）

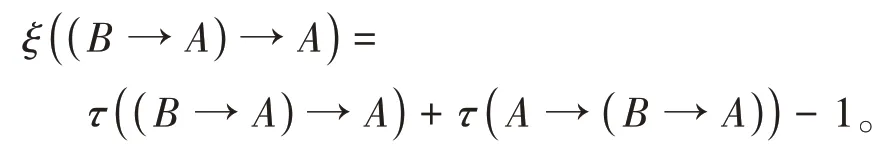
由定义1.1（K4）知

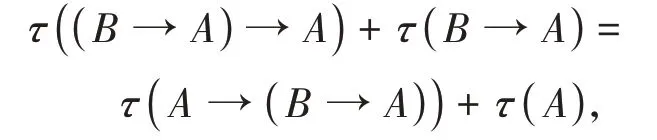
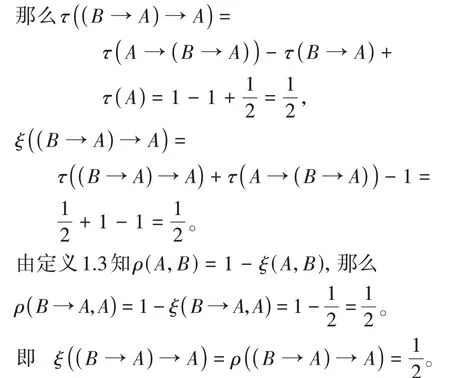
得证。

3 结束语

本文讨论了谓词逻辑系统K*∀的相似度及伪距离，研究了一阶闭逻辑公式的相似度和伪距离的性质及运算性质，为之后研究谓词逻辑系统K*∀的发散度、相容度等奠定了一定基础。