解变分不等式问题的一种半压缩惯性投影算法
陈晶晶,王圆圆,杨延涛
(延安大学数学与计算机科学学院,陕西 延安 716000)
设H为实的Hilbert空间,和‖⋅‖分别表示H中的内积和范数,C⊂H为非空闭凸子集,A:H→H是一个给定的映像,经典变分不等式问题VI(C,A)就是寻求一 点x∗∈C,满足不等式A(x∗),x-x∗≥0,∀x∈C。如果A:H→H是一个单调映像,即Ax-Ay,x-y≥0,∀x,y∈H,则称变分不等式问题为单调变分不等式。
文献[1-9]研究了变分不等式理论在解决科学问题中的应用;文献[10-12]提出了求解变分不等式问题的收缩投影算法;文献[13-15]提出了求解变分不等式问题的次梯度超梯度算法;文献[16-18]介绍了带惯性项算法的起源及应用;文献[19-20]研究了不动点集与变分不等式解集的公共元问题。
文献[11]提出了求解变分不等式问题的惯性收缩投影算法:
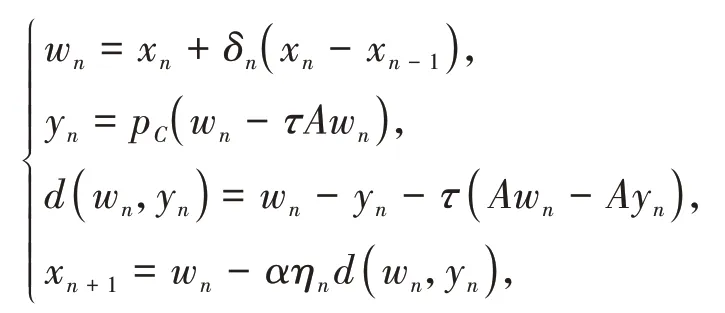
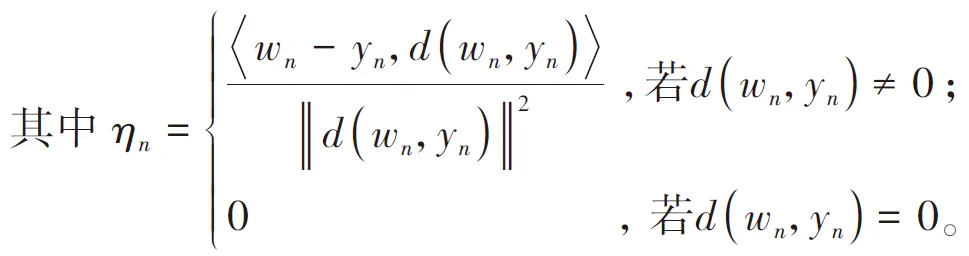
并在适当的条件下证明了由迭代序列产生算法的弱收敛性。
最近文献[13]引入了一种λ-半压缩映像,证明了求解变分不等式问题的强收敛性,使得迭代算法更具有效性和实用性。本文受文献[4,11-13]的启发,提出了一种半压缩惯性投影算法,用以寻找带有半压缩映像的不动点集与单调变分不等式解集的公共元。使用新的分析技巧,证明了所提出的算法强收敛于该公共元。最后,通过数值实验验证了该迭代算法的有效性和实用性。
1 预备知识
设H为实Hilbert空间,H中的内积和范数分别表示为和‖⋅‖。用xn⇀x表示序列{xn}弱收敛到x,xn→x表示序列{xn}强收敛到x。设C为H中的非空闭凸子集,则∀x∈H,C中存在唯一的最近点,用PC(x)表示,即。Fix(T)表示λ-半压缩映像T:H→H的不动点集,即Fix(T)={x∈H|T(x)=x}。
定义1.1[3]I-T在原点是次闭的:假设T:H→H为非线性算子并且Fix(T)≠∅,若对∀{xn}⊂H,满足xn⇀x且(I-T)xn→0,则有x∈Fix(T)。
定义1.2[4]对映像A:H→H称为
i)L-Lipschitz连续,如果存在常数L>0,满足‖Ax-Ay‖≤L‖x-y‖,∀x,y∈H;
ii)单调的,如果Ax-Ay,x-y≥0,∀x,y∈H;
iii)λ-半压缩,如果存在常数0≤λ≤1,对∀x,y∈H,z∈Fix(A),
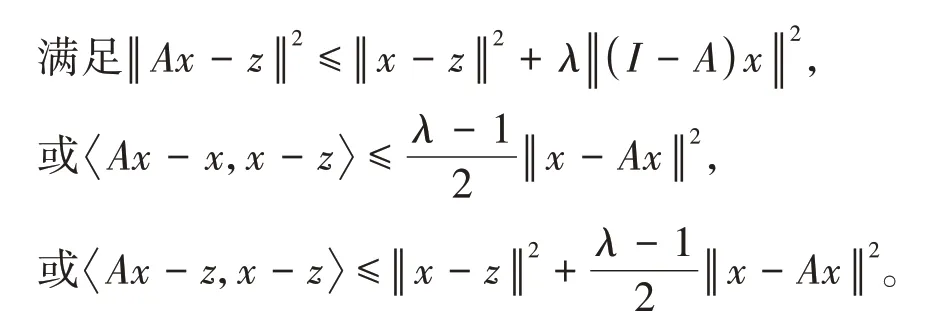
引理1.1[5]设H为实的Hilbert空间,则
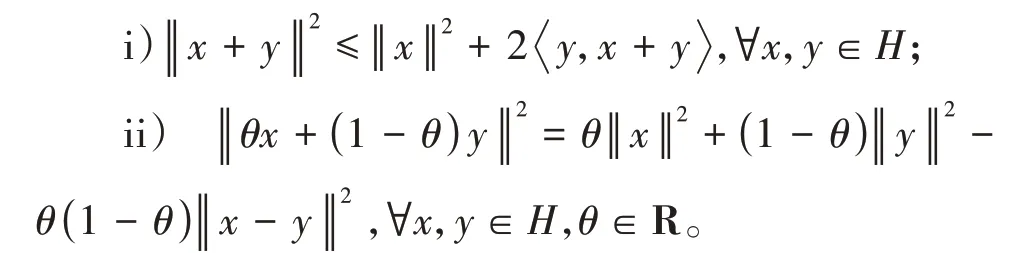
引理1.2[6]设C为H中的非空闭凸子集。对于距离投影PC:H→C有
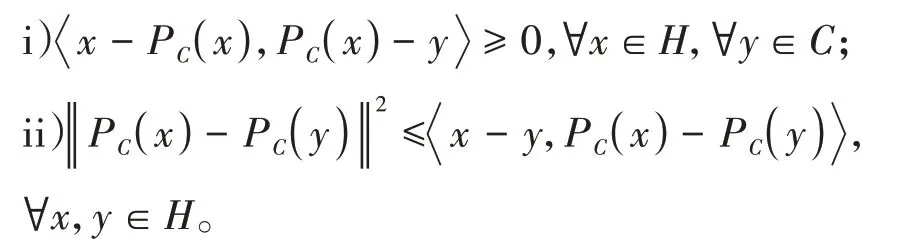
引理1.3[7]设{bk}为非负实序列,且存在子序列使得对∀j∈N都成立,则存在非递减序列使得,并且对k∈N充分大时都满足如下性质
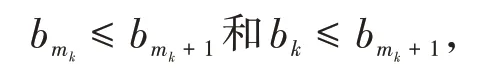
其中mk是集合{1,2,…,k}中的最大数n,使得满足bn 引理1.4[8]设{an}和{θn}为非负实序列且{θn}。如果存在序列0,当N>0时使得成立,则有。 引理1.5[9]假设T:H→H是λ-半压缩的满足。令Tη=ηT+(1-η)I,其中I是恒等映像,η∈(0,1-λ),则有 iii)Fix(T)是一个闭凸集。 假设以下条件成立: (C1)算子A:H→H是L-Lipschitz连续的单调映像; (C2)算子T:H→H是λ-半压缩映像以及IT在原点次闭; (C3)Fix(T)∩VI(C,A)≠∅; (C4)设{εn}和{βn}为正序列,使得=0,并且序列{θn}⊂(0,1),=0,,序 列{βn}满 足{βn}⊂(a,b)⊂(0,(1-λ)(1-θn)),其中a>0,b>0。 算法2.1一种半压缩惯性投影算法 步骤1选取初始点x0,x1∈C,令n=1。计算 步骤2计算yn=PC(wn-τn Awn),其中τn为使τ∈{γ,γl,γl2,…}成立的最大的τ,参数γ>0,l∈(0,1)并且满足, 步骤3计算dn=wn-yn-τn(Awn-Ayn); 步骤4计算zn=wn-αηndn, 步骤5计算 步骤6令n=n+1且返回步骤1。 引理2.1[22]假设(C1)-(C3)成立,根据Armijo搜索程序有。 引理2.2设{zn}由算法2.1迭代产生,假设(C1)成立,对于u∈VI(C,A),有 证明由A的单调性及u∈VI(C,A)得 由zn,dn的定义,yn=PC(wn-τn Awn),式(5)及引理1.2得 使用Cauchy-Schwarz不等式、dn的定义及式(2)得 由dn的定义、三角不等式‖x+y‖≤‖x‖+‖y‖及式(2)得 将式(7)与式(8)代入式(3)得 由zn的定义可得 将式(3)代入式(6),结合式(10)得 结合式(7)与式(9)得 定理2.1假设(C1)-(C4)成立,则由算法2.1产生的迭代序列{xn}依范数强收敛到 证明第一步证明序列{xn}、{wn}、{zn}有界。 利用引理2.2得 故∃M1>0使得 由式(11)、式(13)和wn的定义得 使用xn+1的定义及三角不等式‖x+y‖≤‖x‖+得 由式(11),λ-半压缩映像性质以及βn⊂(0,(1-λ)(1-θn))得 将式(14)与式(16)代入式(15)得 因此序列{xn}是有界的,则{wn}和{zn}有界。 第二步证明 使用xn+1的定义、定义1.2、引理1.1及{xn}有界得 由引理1.1得 由引理2.2、式(19)及式(20)得 整理得 第三步证明 令Sn=(1-βn)zn+βnTzn,利用λ-半压缩映像性质,有 结合式(11)与式(22),有 由Sn=(1-βn)zn+βnTzn,有 使用xn+1的定义、引理1.1、Cauchy-Schwarz不等式、式(23)及式(24),有 情形1假设∃N∈N,有,∀n≥N。 由式(12)与式(18),有 使用引理2.2,有 结合式(12),有 故由‖wn-zn‖→0,有 使用三角不等式及式(28)得 使用wn的定义、Cauchy-Schwarz不等式以及式(1),有 结合式(21)与式(30),有 式(31)也可写为 由于{xn}是有界的,则存在{xn}的子序列{xnj}有xnj⇀p, 由式(27)与式(33),有wnj⇀p。 下证p∈VI(C,A)。 由yn=PC(wn-τn Awn),引理1.2得 由式(26)与式(34)得 由于wnj⇀p,故有 使用式(25)、式(36)及定义1.1得p∈Fix(T),因此p∈Fix(T)∩VI(C,A)。 由u的定义得, 再使用式(32)与引理1.4得 因此证得xn→u,n→∞。 由引理1.3知存在一个非减序列{mk}有 由式(12)与式(18),有 再使用引理2.2,有 由式(12)、式(31)及式(37)得 本节将对所提出的算法与已有算法进行了一些对比数值实验。所有代码均在MATLAB R2016a和windows10系统下运行,当‖xn-x∗‖≤ε时,迭代停止。用“IPCM”、“TEGM”、“TIPCM”分别表示文献[11]中的算法3.1、[22]中的算法2及本文的算法2.1。 例3.1定义算子A:Rn→Rn为A(x)=Mx+q,M=NNT+P+D,其中N是n×n阶矩阵,P是n×n阶斜对称矩阵,D是n×n阶对角矩阵,定义算子T:H→H为Tx=。 由此可见算子A是单调的并且Lipschitz连续,L=‖M‖,算子T:H→H为λ-半压缩映像并且在原点次闭,当可行集C={x=(x1,x2,…,x50)∈R50:-2≤xi≤2,i=1,2,…,50}时 即x∗=(0,0,…,0)T。 例3.1来源于文献[23],选取ε为10-7迭代初始点为x0=x1=(1,1,…,1)T,矩阵N和P中的元素在[-2,2]随机取值,对角矩阵D的对角元素在(0,2)中取值,选取q=0。 数值对比结果见图1。 图1 例3.1中‖xn-x*‖随迭代时间变化图 例3.2设H为实数空间,C⊂[-1,1]⊂H,定义算子A:H→H为,算子T:H→H为。 由此可见算子A是单调的并且Lipschitz连续,T为λ-半压缩映像(λ∈(0,1))并且在原点次闭,Fix(T)∩VI(C,A)={0}即不动点集与单调变分不等式解集的公共元为x*=0。 对例3.2选取ε为10-8,迭代初始点为 数值对比结果见图2。 图2 例3.2中‖xn-x*‖随迭代次数变化图 通过对算法2.1的数值实验结果与文献[11]及[22]中的数值实验结果对比(见图1,图2),可以看出半压缩惯性投影算法优于IPCM算法和TEGM算法,并且在不需要预先知道Lipschitz常数的条件下,证明了算法2.1的强收敛性。由此进一步验证了算法2.1的有效性和实用性。 本文结合半压缩映像和惯性收缩投影方法,借助Armijo线性搜索程序获取步长,提出了一种求解单调变分不等式问题的半压缩惯性投影算法,用以寻找带有半压缩映像的不动点集与单调变分不等式解集的公共元。该算法的优点是不需要预先知道Lipschitz常数,证明了所提的迭代算法强收敛于该公共元,同时通过数值实验证明了本文所提迭代算法的有效性。本文所得结论是对现有文献结论的改进和推广。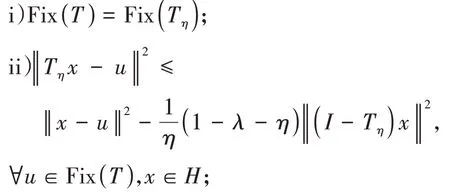
2 主要结果




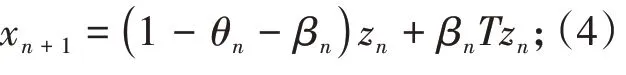
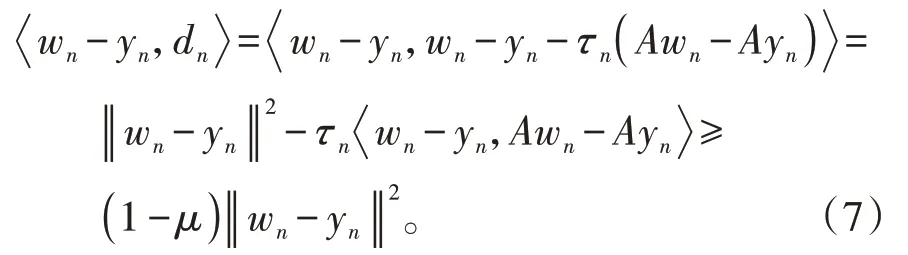
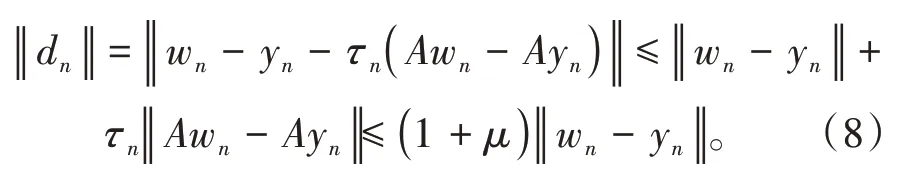
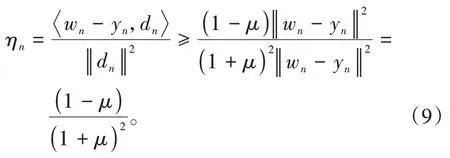
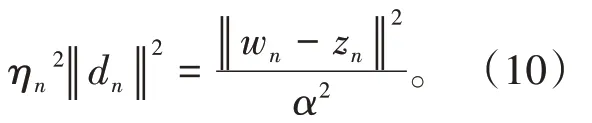
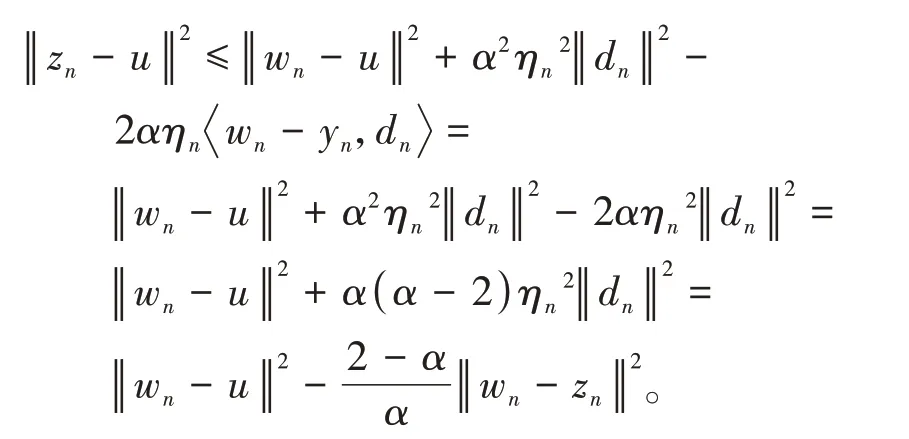
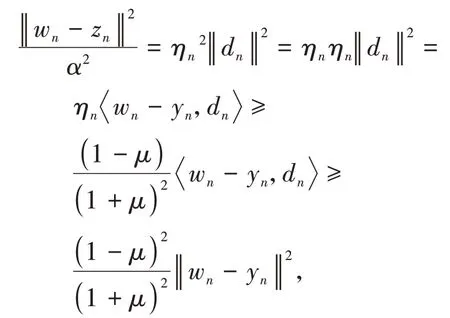
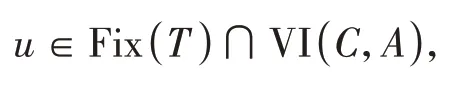
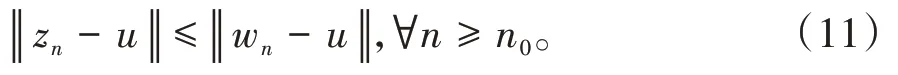
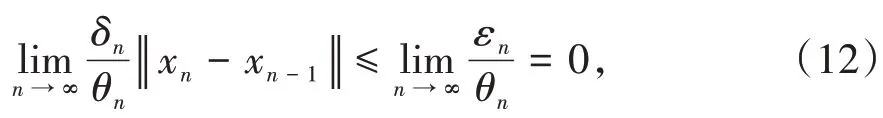
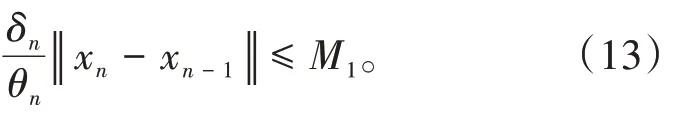
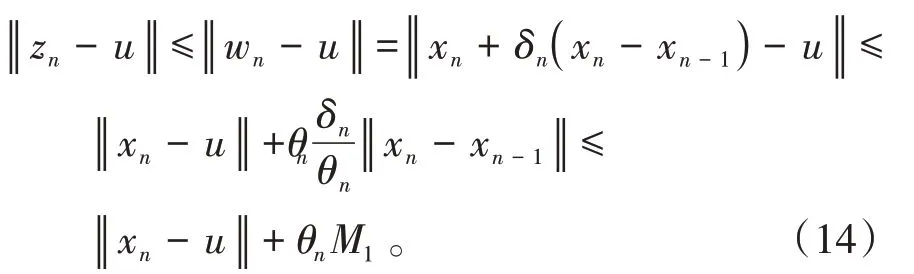
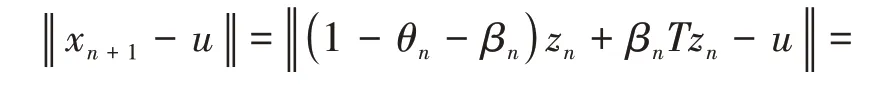
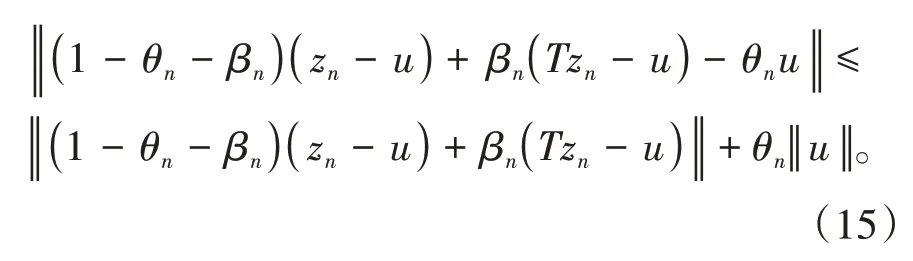
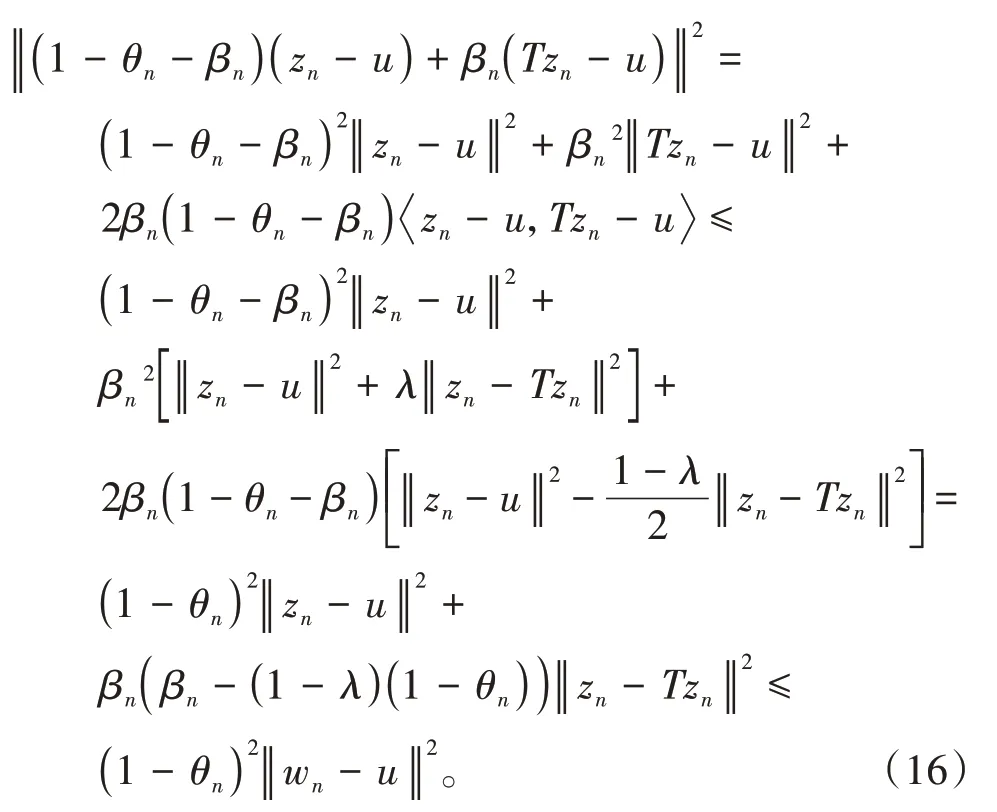
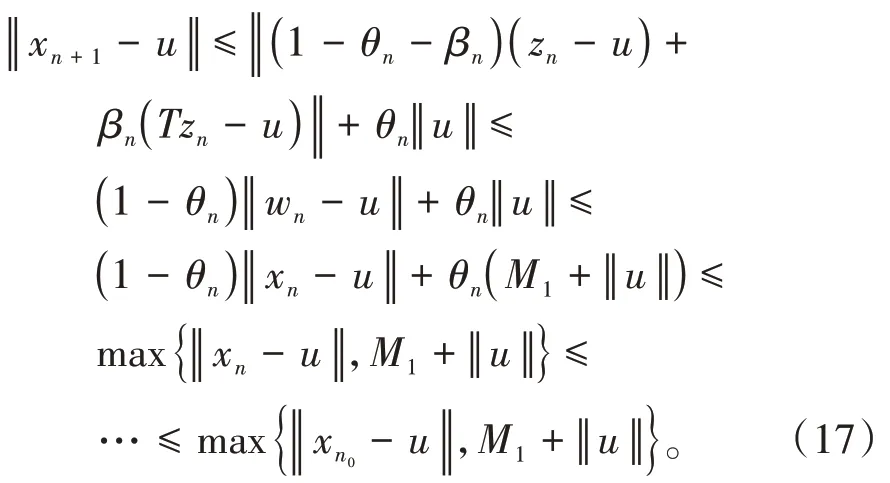
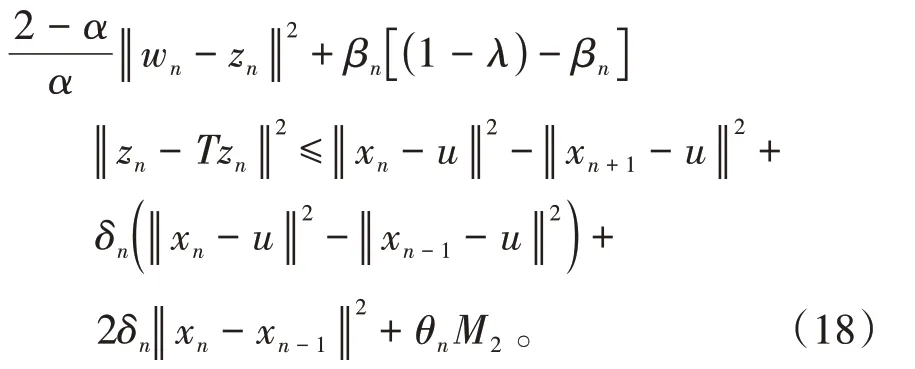

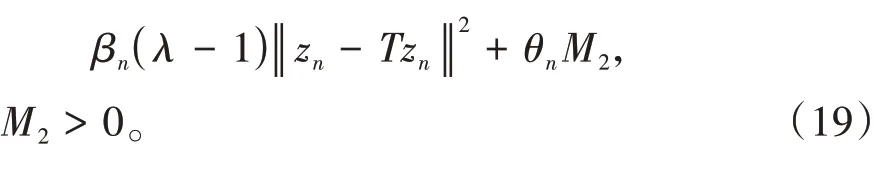
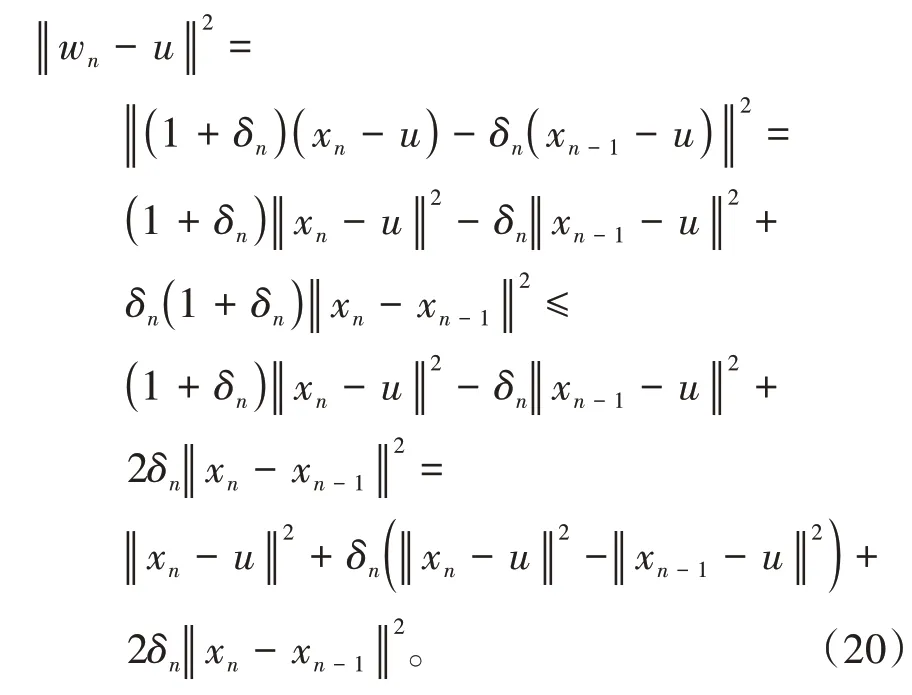
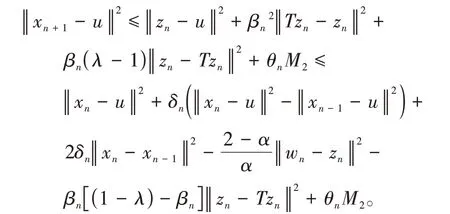
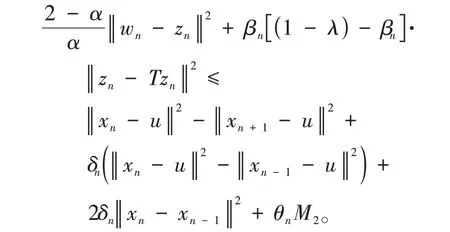
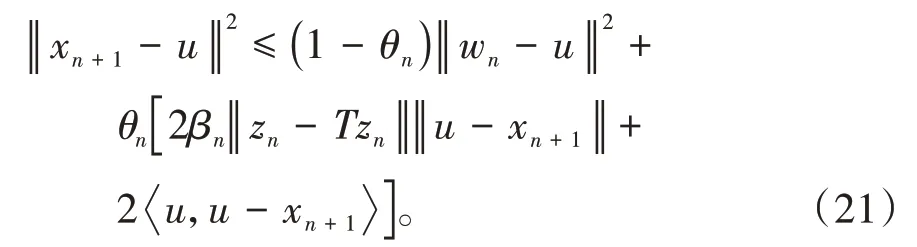
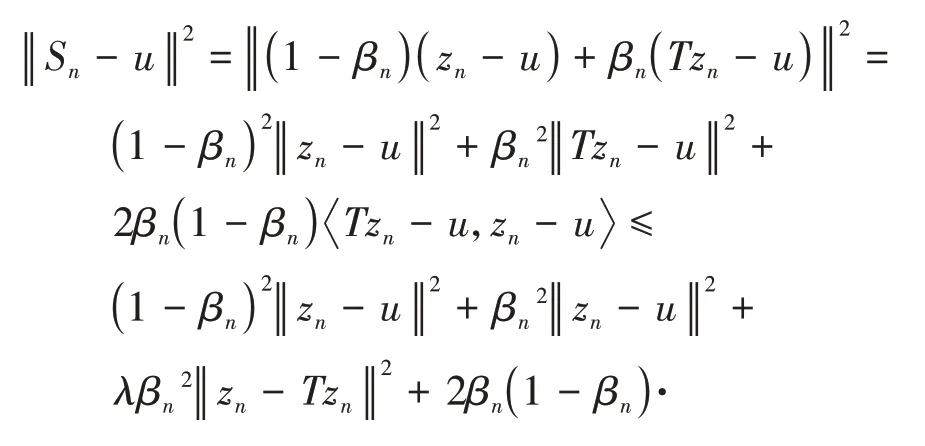
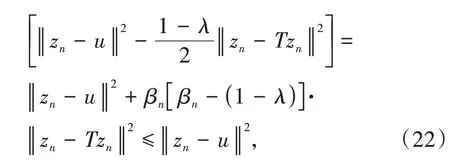
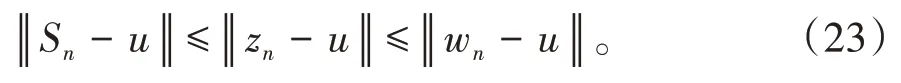
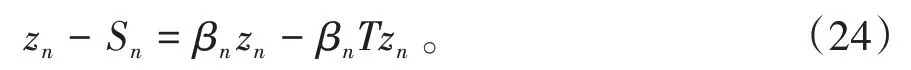
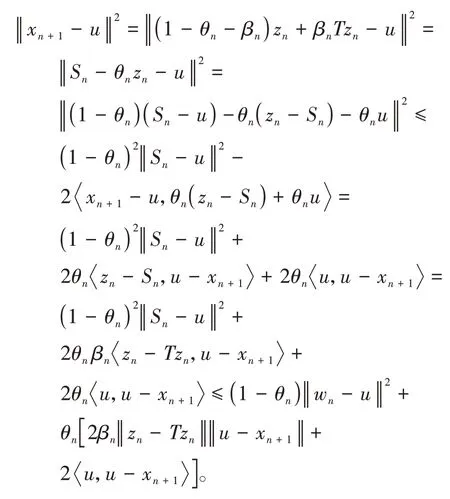
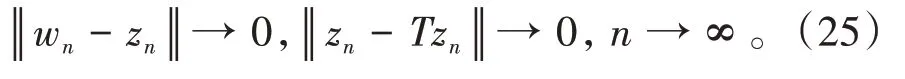

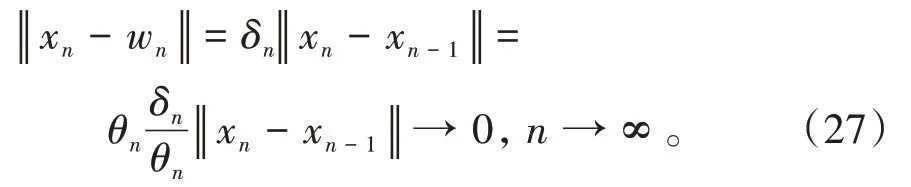
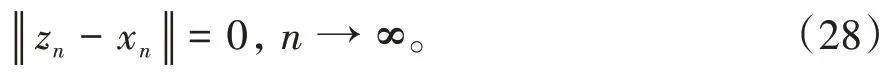
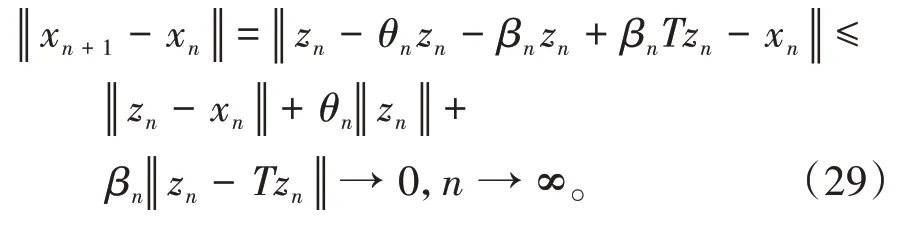
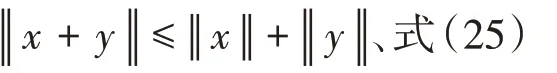
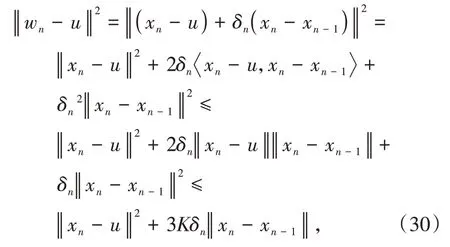
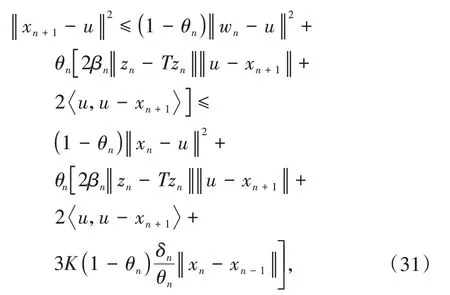
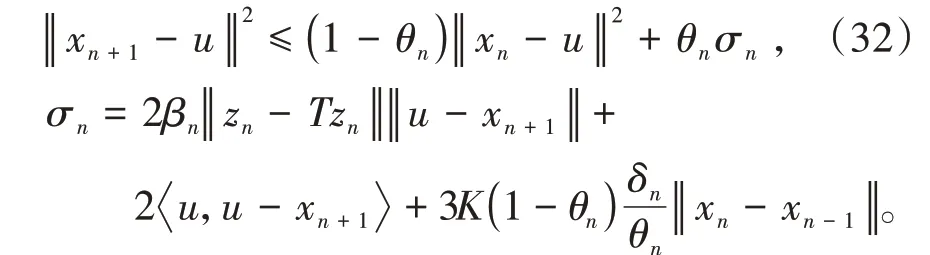
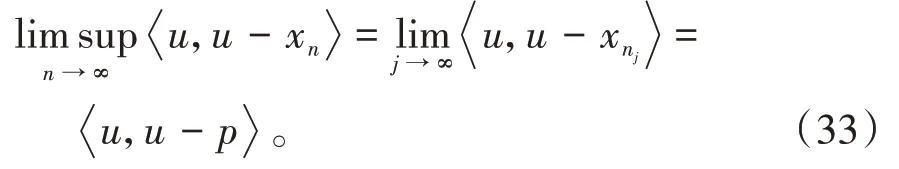
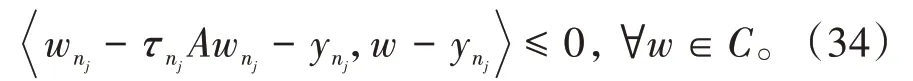
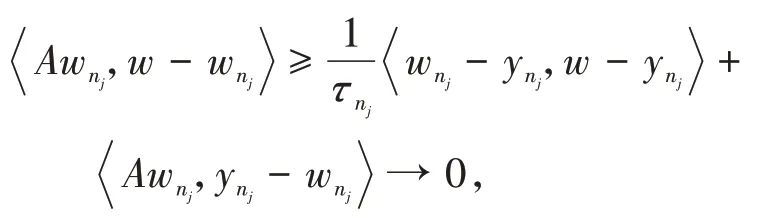
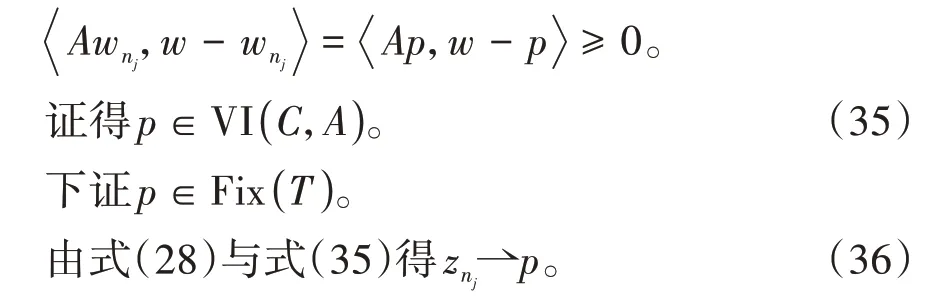
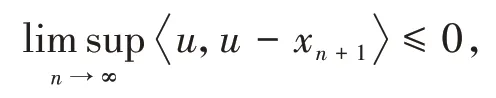
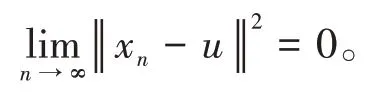
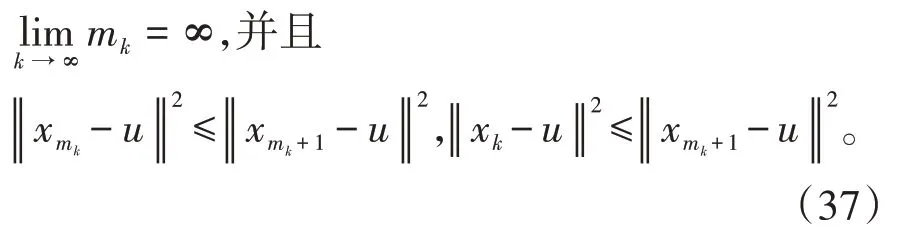
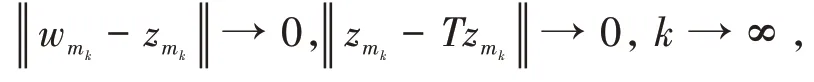
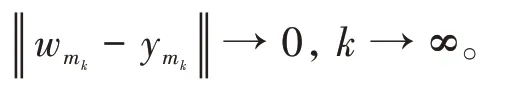
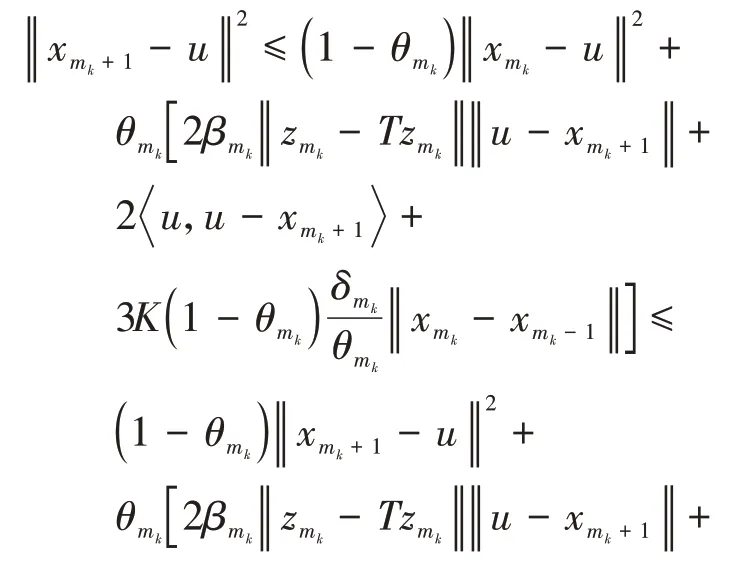

3 数值实验
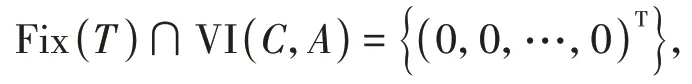
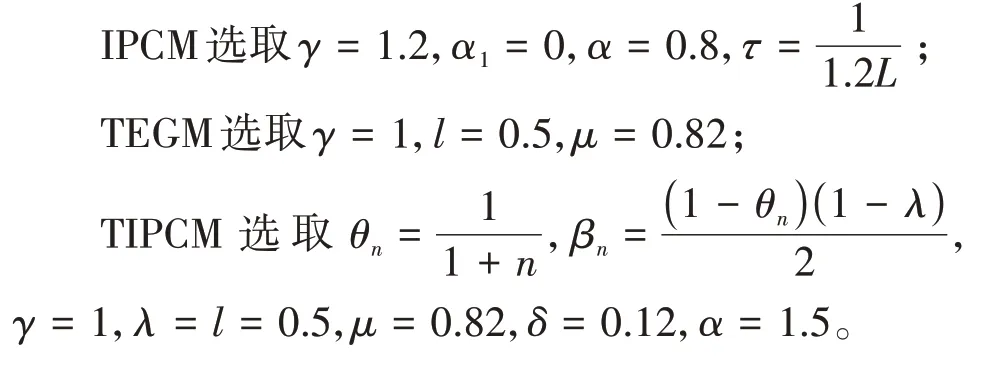

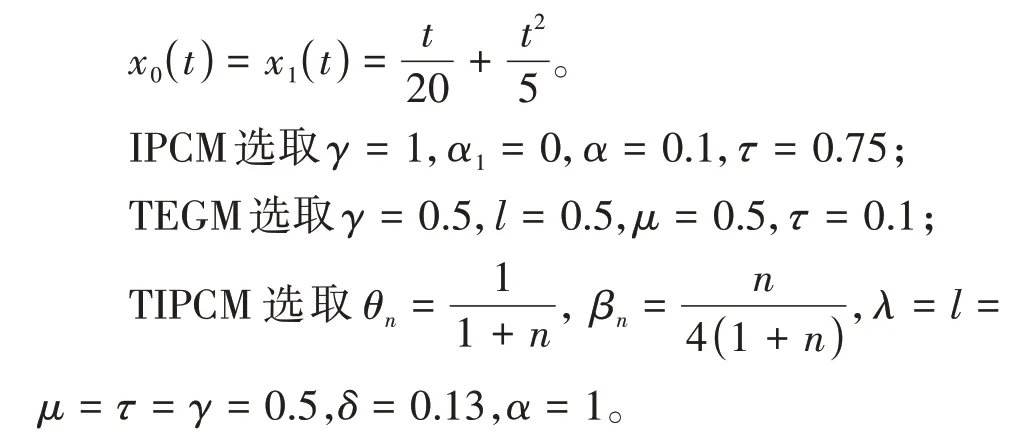

4 结论

