浅谈实体建模：历史、现状与未来

邹 强

浅谈实体建模：历史、现状与未来

邹 强

(浙江大学CAD&CG国家重点实验室，浙江 杭州 310027)

实体建模技术是CAD软件的“功能心脏”，相关基础理论与算法是CAD发展历史上最关键的成果之一，成功回答了为使计算机能够辅助产品设计与制造，需在计算机中存什么几何信息以及怎么存的问题。本文对实体建模的主要历史发展脉络做了简要介绍，同时对各发展阶段的关键问题以及研究现状进行了讨论，最后选取了3个方向对实体建模的未来做出展望,重点关注从Computer-Aided Design到Computer-Automated Design的发展趋势。

CAD；几何建模；实体建模；参数化建模；直接建模；结构建模；智能CAD

1 概 述

实体建模技术是计算机辅助设计(computer- aided design，CAD)领域60余年发展过程中最重要的成果之一，回答了CAX (computer-aided X)任务中最基本的问题：为使计算机能够辅助产品设计制造，需在计算机中存储哪些几何信息以及怎么存。

实体建模算法库组成了CAD软件的几何建模内核。而该内核如何做到自主可控，弥补与国际主流内核如Parasolid，ACIS的巨大差距，是解决我国所面临的工业软件“卡脖子”问题的重点。为此，实体建模技术对我国具有重要意义。

本文将梳理实体建模的历史发展脉络，叙述其基础理论、关键算法与难点、以及这些难点的解决现状。同时，本文还将对实体建模的未来作出展望，重点关注Computer-Aided Design向Computer- Automated Design发展的趋势。

1.1 从CAD到几何建模

产品即人造物理实体，产品模型指这一实体的计算机表示(即一种数据结构)，而CAD即是使用计算机来构建、查询和编辑产品模型。CAD的概念于上世纪50年代末在MIT被提出[1]，主要为满足：

(1) 构建产品的计算机模型并对之进行处理，以满足二战后发展起来的数控机床对自动生成加工路径的需求[2]，实质上是为了满足机器与机器间的协作需求；

(2) 构建一个可以让人和计算机一起协作的设计系统，其中人负责创造性任务，而计算机负责机械式任务[3-4]，如图1所示，实质上是为了满足人与机器间的协作需求。

图1 CAD系统中人与计算机的分工

从这2个需求(尤其是第2个)出发，CAD的具体内涵会非常丰富。但不久后，人们意识到CAD应当聚焦于产品建模、产品分析和产品制造这3个内容，因其更基础、本质[3]。但同期也有其他领域在研究产品分析和产品制造，这3个内容最终分流成今天熟知的CAD，CAE (computer-aided engineering)和CAM (computer-aided manufacturing)。

具体到CAD，产品建模的任务旨在需要构建能够支撑产品全生命周期所需全部信息的数字模型。这些信息以产品的几何形状为核心(图2)，并伴有材料、工艺等非几何信息[5]。在实际数字模型中，材料、工艺等信息均可在几何模型的基础之上以标记的形式来存储。正因为如此，CAD建模往往重点关注几何建模。到目前为止，主要的CAD几何建模方法有：线框建模、曲面建模、实体建模、参数化建模以及直接建模，如图3所示。

图2 产品几何信息在产品全生命周期中的作用

图3 CAD几何建模方法发展总括图

1.2 从几何建模到实体建模

在众多几何建模方法[6]中，线框建模到曲面建模再到实体建模是CAD建模技术发展的初期阶段，其主要关注产品几何信息该以何种数学模型来表示的问题。具体的发展脉络可参见文献[7]。

其中，线框模型，不管是2D还是3D，利用产品的边或轮廓来描述几何形状。2D线框模型直接复制传统工程制图，也是第一代CAD原型系统“Sketchpad”所采用的方式[8]。3D线框模型的提出是为了解决2D线框模型每变换一个视角，都要重新绘制的问题(通过对3D线框模型进行投影操作，可自动得到任意方向的视图)。然而，线框模型存在2个重要缺陷：歧义性和无效性，如图4所示。无歧义性和确保有效性对CAD建模至关重要，因为CAD追求模型的真实性，与追求真实感的图形学不同[6,9]。

图4 线框模型的缺陷((a)歧义性；(b)无效性)[7]

为解决上述问题，人们提出曲面模型，对线框模型进行“蒙皮”[10]。同时，二战后工业界对汽车和飞机等复杂曲面设计制造的需求也促进了曲面模型的发展[6]。人们提出了一系列巧妙的曲面表示和操作方法，从Coons曲面到Bezier曲面到B-spline曲面再到其改进型NURBS曲面，详细地发展脉络见文献[11]。

然而，仅有曲面信息仍无法彻底解决歧义性和无效性问题，如真实世界中并不存在零厚度物体，而且每个物体都有内外之分。为此，实体模型被提出[12-13]，其特点在于对产品几何信息进行了完整的表示，从点到边到面再到体。因其具有信息完整性，任何几何性质(如转动惯量)也都可以被计算机自动计算出来[14]。

1.3 从实体建模到参数化/直接建模

实体模型因其信息完整性而适合表示产品几何信息。然而，基本的实体建模方法，即CSG (constructive solid geometry)[15]和B-rep (boundary representation)[16]，存在重要缺陷：实体模型一旦被构建便难以修改[17]。因此，早期实体建模方法一般仅被用作记录已经设计好并且不会发生变动的产品，对整个设计过程，尤其是早期概念设计阶段，帮助不大[7,18]。

为解决这一问题，参数化建模在80年代末被提出[2]。其基本思路是在实体模型的基础上添加一层关联(associativity)信息，即在组成实体模型的几何元素之间添加关联信息，如此，模型上的局部变动可以按设计好的方式自动传播到模型的其他区域[18]。关联信息一般以几何约束(如距离、相切、共轴等)的方式给出，并使得模型形状被参数化到某几个控制参数上，即模型形状是这些控制参数的一个函数[19-20]。至此，通过在实体建模之上添加一层关联信息，人们获得了参数驱动的实体模型变动能力。

值得一提的是，人们又在“实体+关联”的基础之上，添加一层语义信息，形成了特征建模方法[2,21-22]。简而言之，特征是对实体模型中几何元素的一种归组，同组元素会被一起引用，并被赋予特殊地设计或制造语义。

总之，参数化建模给实体建模带来了3个益处[18,20,23]：①自动的变动传播；②模型/设计重用；③设计、制造语义在实体模型中的表达。

参数化建模虽然有效，但模型只能在预先设计好的空间(由几何约束系统决定)里变动[24-25]，使得参数化建模难以适用需要对模型进行自由编辑的场景，尤其是在概念设计阶段[17,26-29]。针对这一问题，直接建模在2010年左右被提出[30]。与参数化建模中通过参数调整来间接式地修改实体模型不同，直接建模允许设计师对实体模型的几何元素进行直接式的交互编辑。直接建模方法有3个优点：

(1) 直观的交互方式使其能够适用于概念设计；

(2) 极高的建模自由度和效率，因为直接建模操作能将一个实体模型变形到任意形状；

(3) 高效的模型更新，因其采用局部模型更新方法。

上文简述了实体建模技术的由来与历史，下面将对实体建模、参数化建模和直接建模的关键技术进行讨论。

2 实体建模1.0 (早期发展)

如前文所述，产品几何信息在产品计算机模型中占据着核心位置。但是在设计领域，尤其是机械设计领域，几何信息的具体内涵和定义是什么？人们在回答这一问题的过程中逐渐形成了实体建模理论与算法体系，简述如下。

2.1 实体数学定义

有界性是指实体的任意点到原点的距离均是有界的。如一个10 mm×10 mm×10 mm的立方体就是有界的，而平面是无界的。这一条件是显然的，现实世界中并不存在无限大的工业产品。

半解析性是指实体的边界由半解析曲面组成。解析曲面指曲面上每点的(某个)邻域可展开成收敛级数。这一约束条件是为了剔除如图5所示的高阶振荡曲面，将实体边界限定为平顺变化的曲面。半解析曲面是指曲面的边也是解析的。这是由于产品边界往往不是由一张曲面就能完整表达的，需要多张曲面缝合在一起才能表达，半解析曲面就是对缝合处的边提出具体要求。

图5 非解析曲面例子[6]

正则性是指实体是三维的，在数学上表达为实体与其内点集合的闭包是相等的，如图6所示。这一约束条件是为了防止实体不包含边界点(not closed)，或者含有一维点集及二维点集，如图7所示。

图6 正则性定义示例

上述3个约束条件虽然可以完整刻画大部分机械产品的形状特性，但仍然允许实体具有非流形(non-manifold)边界。为此，人们又在r-set的基础之上添加了流形边界的约束条件，即实体边界上每个点的邻域都是二维的[34]。这在数学上表达为实体边界上每个点的(某个)邻域和二维圆盘是同胚的，而同胚指2个点集之间具有连续的、一一对应的映射。这一约束条件是为了防止实体出现如图8所示的线接触或点接触。这种情况在现实世界中是不可能的，因为其在接触处具有无穷大应力。

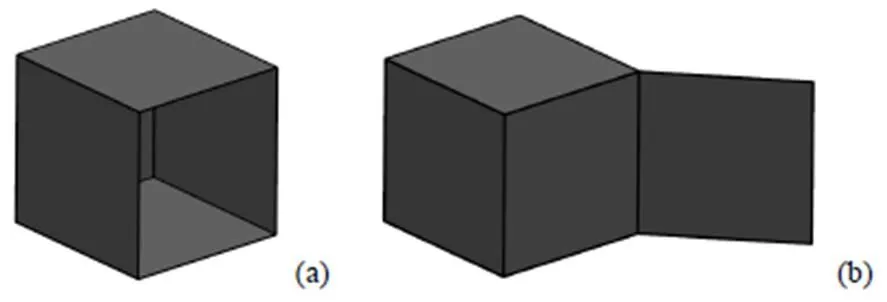
图7 非正则实体图例((a)非闭合模型；(b)带二维点集模型)

图8 具有非流形边界的实体图例

2.2 实体模型表示

上述实体定义是产品几何信息的数学抽象，即数学模型，实体模型是在数学抽象基础之上的计算表示，即计算机模型(本质是一种数据结构)。在过去的50年里，人们提出了多种实体模型格式，详见文献[6,14,35-36]。其中，CSG和B-rep是最常用的。

B-rep实体模型存储实体的边界，实体的内部由边界推导而出(如使用Winding numbers[37]，parity[38]，以及in/out counting[36]等方法)。如图9(a)所示，一个B-rep实体模型实质上仅存储组成该实体的边界面，包括其背后的几何曲面(carrying surfaces)，以及这些面之间的拓扑邻接关系[10]。通过邻接关系，可以对曲面进行裁剪、缝合，最终生成边界面。实际的B-rep数据结构往往会在此基础之上添加一些冗余信息，如顶点、边以及邻接关系，以加快几何查询的速度[6]。

CSG实体模型存储实体的构建历史，如图9(b)所示。其使用布尔操作将多个简单实体模型组合成复杂实体模型[15]。故其主要包含2个操作：体元生成(如立方体、圆柱体)与布尔操作(如体元求交集、求并集)。与B-rep的显式存储方式不同，CSG是一种隐式表示方法，模型内部只存储操作步骤，不存储操作结果，实体最终的形状由所记录的构建历史推导而来[39]。实际的CSG数据结构往往是一个二叉树，其中叶子节点存储体元的定义信息，中间节点存储布尔、刚体变换等操作。

图9 实体模型图例

CSG实体模型的主要优点有：①保证有界性质；②保证边界曲面半解析性质；③保证正则性。缺点有：①无法保证边界的流形性质，如图10所示；②模型表示不唯一(一个模型对应多个CSG树)。

图10 CSG无法保证边界的流形性质[34]

B-rep实体模型的主要优点有：①模型表示具有唯一性；②(理论上)可以表示任意复杂的实体；③由于是显式表示，可直接用于后续模型处理。其缺点有：①无法保证所存储实体模型的正则性和流形性质(一般情况下可保证有限体积性质和半解析性质)；②计算不鲁棒问题；③当模型比较复杂时，存储量比CSG大。

可以看出，B-rep和CSG具有一定的互补性。正因为如此，现代实体建模系统一般采用B-rep和CSG相混合的表示格式[18,40-43]。CSG的二叉树结构作为骨架，B-rep模型替代了CSG中的体元，同时二叉树的中间节点不仅存储操作步骤，还存储部分运算结果，比如重要边界面的信息。存储这些中间信息目的是为了将操作从布尔扩大至一些局部操作，如偏移、圆角等[16,40,44-45]。这些操作需引用被操作对象(即实体模型的某一局部几何元素)，故而对这些对象进行存储或标记至关重要。

2.3 实体建模算法

实体建模算法指构建和编辑实体模型的算法，一般分为3个层次实现：①底层数值算法；②中层几何/拓扑计算；③上层实体操作。

其中上层实体操作主要包括布尔、过渡(圆角/倒角)、偏移、抽壳、扫掠、拔模、修复等1Euler操作文献[16,152]也是实体建模的重要操作，但似乎现代几何建模内核里面的几何操作都不再基于Euler操作来实现了。。这些操作在背后调用中层的几何计算或拓扑判定，主要包括求交、投影、成员判别、排序、曲面拟合等。如，2个B-rep实体模型间的布尔操作实质上调用的是曲面求交和成员判别2个操作。而几何计算/拓扑判定又会调用底层的数值算法来做解算，主要包括线性/非线性方程组求解、数值优化等通用数值算法。

此处不对具体的数值算法、几何计算/拓扑判定或实体操作的研究现状进行详述，而是对其中具有一般性的鲁棒性问题进行讨论。实体建模中的鲁棒性问题主要有3个来源：

(1) 由于底层数值算法存在表示误差(来源于浮点舍入误差)、数值计算误差(来源于数值求解或优化方法，常常伴随计算步骤的增加而累加)以及中层几何计算存在不完全表达误差(来源于利用低阶曲线曲面对高阶曲线曲面进行近似所带来的误差)等表示和计算误差，以其计算结果为基础所做的逻辑性的拓扑判定可能发生不一致的情况，比如交线分支选择错误，邻接关系不对称、无传递性等问题[46-49]。这方面典型的情况有布尔操作时曲面求交误差所引起的成员判别失误。

(2) 即使不存在任何表示和计算误差，拓扑判定结果也可能与几何数据不一致，并最终导致无效的实体模型。这种情况的根本原因在于B-rep数据结构要求拓扑和几何保持一致，才能保证模型的有效性。然而，拓扑和几何数据在B-rep中又是分离的，几何数据的变动不会自动反映到拓扑数据中，反之亦然[50]。正因为此，有些拓扑数据虽然从自身来看是有效的，但和几何一结合就会产生失效模型[51]。这方面典型的情况有模型修复时拓扑修正决策引发如图8所示模型自交(注意不是曲面自交)。所谓拓扑修正是指对无效模型(即：是B-rep模型，但不满足实体条件，如边界不是流形的)的拓扑进行调整，以使之变为有效模型。

(3) 永久命名问题(此处不讨论，详见3.1节)。

从上述讨论可以看出，实体建模中的鲁棒性问题本质是几何-拓扑不一致问题，其原因不全在数值误差，反而更在于拓扑判定的正确性。

为解决由数值误差引起的鲁棒性问题(即来源(1))，一个自然的思路是将底层算法换用精确计算，如符号计算方法、有理数方法等[52-57]，但是这些方法往往在通用性或效率方面存在问题，并不实用。另一个思路是使用容差来保证即使存在计算误差，拓扑判定仍是正确的[49,58-60]，如图11所示。这种方法在理论上可完美解决几何-拓扑不一致问题，实现鲁棒建模，也是工业界所采用的方法，但是目前的容差设计方法主要以人工规则和阈值试错的方式给出，尚缺少系统的方法。特别地，容差会在多个不同局部累积增大，当其相遇时，会发生不一致情况，进而导致错误的拓扑判定。

图11 容差建模((a)对立方体进行裁剪；(b)具有容差的相交线)[58]

总体而言，实体建模1.0 (至80年代末)奠定了实体建模的理论和算法基础。但是基础算法方面仍存在种种问题，尤其是鲁棒性问题，如鲁棒求交、鲁棒圆角等。

3 实体建模2.0 (中期发展)

实体建模在80年代末和90年代迎来重大发展，走向参数化建模[2]。简言之，参数化模型是在前述B-rep与CSG混合模型的基础之上增加了几何约束[20,61]。(几何约束其实早在第一代CAD系统“Sketchpad”上就已使用[8]。)尽管人们尝试了多种参数化建模技术，详见文献[18]，主流的方法由以下3个部分组成[17,62-63]：

(1) 2D草图绘制。用户首先在绘图平面上指定几何图元(点与边)的拓扑，然后在其间添加几何约束[64]。

(2) 3D特征生成。对所绘制的二维草图进行拉伸、旋转等操作，以生成三维实体特征(存储为B-rep模型)，类似于CSG中的体元。

(3) 特征组合。将生成的3D特征与之前的特征进行布尔等操作，使之与CSG类似。

所有特征生成与组合的步骤又被称为建模历史，当其中一个步骤的参数发生变动，所有被记录在建模历史中的步骤都会按顺序更新，并最终生成新的实体模型。于是有了参数驱动的实体模型变动。

从上述3个步骤中可以看出，参数化建模所带来的新问题主要有2个：①如何确保建模历史中所有引用对象的有效性，即所谓永久命名(或拓扑命名)问题；②如何求解用户给定的几何约束系统，即所谓几何约束求解问题。当然，还有特征识别、维护等问题，由于这些问题与高层语义更相关，而非底层的拓扑、几何、约束等，此处不展开讨论，参见文献[22,65-66]。

3.1 永久命名

在参数化建模中，当一个参数值发生变动，CAD软件就会根据建模历史重新生成模型。由于特征间具有“父-子”依赖关系，若这种关系在重生成过程中发生丢失或产生歧义，那么模型重生成就会失败，如图12所示。这一问题在90年代初被发现[24,41,67]，随后人们提出了多种方法[68-69]，但这方面的研究很少，目前尚无系统地解决方案。

图12 永久命名问题示例[18](此处，引用歧义指倒角操作所引用的边在被槽一切为二之后，对哪条边施加倒角操作存在歧义)

所有永久命名方法均致力于寻找B-rep模型在参数变动下的不变量。一种典型的不变量是以几何元素间的拓扑关系为主，辅以形状类型或相对位置，这方面典型的工作见文献[70–72]。后来，人们又在此基础上添加建模历史，即几何元素的生成与变动历史，提高命名的鲁棒性，这方面典型的工作有文献[72-78]。这一方法目前已经被工业界广泛使用。值得一提的是，其中文献[75]的工作来自于我国华中科技大学，已成为永久命名方面的经典算法。

除上述方法外，Shapiro将拓扑学引入永久命名的研究中，提出了拓扑不变2实质上，Shapiro给出的条件是允许拓扑变化的，但是这种变化需满足模型的边界面发生连续变形。的必要条件[41,79-81]，这为研究各种永久命名方法的适用范围提供了理论基础。另外，人们还从特征语义的角度研究了参数变动下的不变量[82-83]，从限定参数变动域的角度来避免出现永久命名问题[84-86]。然而，这些工作多以纯理论研究为主，尚未应用于实际。

混合几何、拓扑和建模历史来处理永久命名问题是目前工业界常用的方法，如几何内核Open CasCade即采用类似文献[70]中的方法。然而，这类方法往往需要混杂ad hoc规则，不够系统，也不能完整解决永久命名问题，尤其是难以处理发生大拓扑变动的情形。永久命名问题亟需新的思路，形成一个系统的解决方案。

3.2 几何约束求解

几何约束求解涉及2大问题：欠、过约束系统处理和恰定约束系统分解。其中约束处理是为了将用户输入的一个非恰定的约束系统修正为恰定约束系统，而约束分解是为了将一个大的约束系统分解为多个子系统，然后分别解算，以提高求解效率。

3.2.1 几何约束分析与分解

在过去的30余年里，人们提出了多种方法来分析几何约束系统的约束状态以及对其进行分解[43,87-88]。其大致可以分为4类：直接求解法、逻辑推演法、图匹配法和扰动法。其中，直接求解法最为简单，利用数值计算方法(如Newton-Raphson和homotopy)或者符号计算方法(如Grobner bases和Wu-Ritt triangulation)对几何系统进行直接解算。如果求解成功，则为恰定约束；如果失败，则其约束状态由求解中间过程信息给出。目前，此类方法由于计算效率太低已经很少被实际采用[43]。

逻辑推演法[89-90]以一组几何公理和推演规则为基础，测试一个给定的几何约束系统是否可以被逻辑推演出来。如果成功，那么该系统是恰定的；如果存在额外的几何约束，那么该系统是过约束；反之，该系统为欠约束。这种方法本质上是将数学中的公理化思想应用到几何约束分析与求解中，具有很高的数学价值。然而，目前所制定的几何公理和推演规则离能够实际应用还远远不够。

与上述直接处理几何约束的方法不同，图匹配法将一个给定的几何约束系统首先转化为一个图，然后以图上的性质来间接地反映原几何约束系统的性质。该方法有2条发展脉络，其一致力于在图中识别出一些特殊子图，这些子图会对应固定的几何形状或约束求解策略。这一思想首先由OWEN[91]提出，随后BOUMA等[92-94]对子图种类进行了有效扩充。其二致力于使用自由度分析来提取图中恰定的子系统。这一思想首先由BARDORD[95]和SERRANO[96]提出，随后AIT-AOUDIA等[97-99]对具体地提取算法做了补充。2001年文献[87]针对这 2条脉络进行了详细的总结，并使用“分解-组合”这样一个抽象框架来统一表述上述方法。这之后，图匹配法虽然仍有所发展，如文献[100]，但整个基础框架保持不变。值得一提的是，我国中科院和华中科技大学的学者在这类方法上也做出了重要贡献[101-102]。

尽管图匹配法在工业界得到了广泛应用(如DCM和LGS)，但其存在重大缺陷：不能处理具有约束依赖(除了最简单的结构性依赖)的系统[103]。其原因在于当几何约束系统转化成图后，只有约束系统内的组合类信息(combinatorial information)被保留，所有几何信息均被丢弃，而很多约束依赖却与几何约束系统当时所处的几何形状息息相关。

为克服上述缺陷，扰动法[103]于2006年被提出。其基本思路是对约束系统的变量施加一个微小扰动，然后分析约束系统的反应，不同的反应模式就对应了不同的约束状态。扰动法最重要的结论是：由于几何约束系统是非线性的，其反应随扰动施加位置的不同而有所变化，但是在一些代表性位置，扰动法的分析结果具有一般性[103]。文献[104]给出了计算代表性位置的算法。这一方法由MICHELUCCI等[103,105-106]首先提出，最近在文献[107-108]中得到实际应用，在文献[30]中提升了其通用性(该问题讨论见文献[109])。完整解决其通用性问题尚需新的发展。

总体而言，几何约束分析与分解虽然在算法和应用上取得了长足进步，但几个根本问题一直未得到解决：

(1) 仍缺少有效的恰定约束状态判定准则。目前广泛使用的基于自由度的判定准则缺乏理论保证，尤其是针对3D几何约束系统。实际例子也已经多次证实此类准则会失效[103,110]。

(2) 仍无法做到最优分解。整个约束系统求解的效率由最大子系统的规模决定，因而需要将每个子系统的规模降到最低，但目前尚缺少有效的算法。

(3) 仍无法高效求解大型3D几何约束系统。其原因一方面是因为缺少有效的判定准则，约束分解的鲁棒性问题突出；另一方面，传统基于分解的思路难以应对大型系统，也许并行计算是一个突破口。

(4) 仍无法自动处理多解选择问题。理论上，恰定几何约束系统解的个数与约束数量是指数关系。如何自动在这么多解中选择出用户想要的解是长久以来一直存在的一个问题，这方面研究很少，而工业界多采用基于规则的方法，尚缺少系统的解决方案。

3.2.2 几何约束系统处理

约束处理的核心任务是在系统中添加或删除约束，以消除欠、过约束状态，形成恰定约束系统，其难点在于：能够满足条件的约束往往不唯一，需要对候选约束进行设计语义方面的评价并依此做出排序。

与约束分析和分解相比，约束处理方面的研究工作较少，进展也很小[88,111]。初期的典型工作如文献[98,112]，其思路是应用文献[113]中的最大加权方法，即给每个候选约束赋予一定的权重，然后从中选择那些能够形成最大加权总和的约束子集。这一方法的有效性严重依赖于权重的设计，而现有工作多采用基于ad hoc规则的方法，很难具有通用性。也有如文献[114-116]的方法是基于前述图匹配法来对约束进行选择，这显然会继承图匹配法的固有缺陷。还有如文献[117-120]的方法是基于纯人工规则，如约束类型等，这些策略也使其缺乏通用性。最近如文献[107-108,121]的方法是基于扰动法来做选择，但目前的进展还局限于简单约束系统[107]、纯过约束系统[108]，或一般约束系统但不能完全自动化[121]。

总之，目前尚缺少有效的智能约束处理方法，现有方法仍处于初级发展阶段。近来人工智能的快速发展也许会给这一领域带来新的进步。

4 实体建模3.0 (近期发展)

直接建模技术是实体建模继参数化建模后又一重要进展。此方法虽然于2010年左右由工业界正式提出，但其相关的技术可追溯到80年代由学术界提出的局部操作概念[16,25,45,122-123]。所谓局部操作是指对B-rep模型的局部几何元素直接进行编辑的方法，例如圆角、偏移等。直接建模技术就是在tweaking这一局部操作的基础之上发展起来的。Tweaking允许用户对B-rep模型的边界面进行旋转、平移等修改，但边界面的变动被严格控制在不破坏原有拓扑关系的范围内。

直接建模放松了上述限制，以获得对模型进行任意编辑的能力(图13)，并将之重命名为push-pull操作。Push-pull操作是初期直接建模技术唯一支持的操作，但目前已得到了极大地扩充，如删除面操作等。从最近的发展来看，任何允许用户对实体模型的几何元素(点、边、面)进行直接编辑(包括移动、删除、合并、分割等)的操作都可以归到直接建模[30]。

图13 直接建模图例((a)原模型；(b)编辑后模型[30])

与参数化建模中用户通过几何约束来显式、完整地表达设计意图，而计算机机械式地求解几何约束来更新模型不同，在直接建模中，用户只指定部分几何元素的目标位置(即只表达部分设计意图)，其他几何元素如何协调地进行变动(主要是拓扑更新[30])由计算机自主推断(即计算机补全用户设计意图)。如此，用户得以减负，并获得直观、快捷的模型编辑能力，而计算机是加负，需要变得更智能。如图14所示，如果计算机没有自主性，将得到一个失效模型。

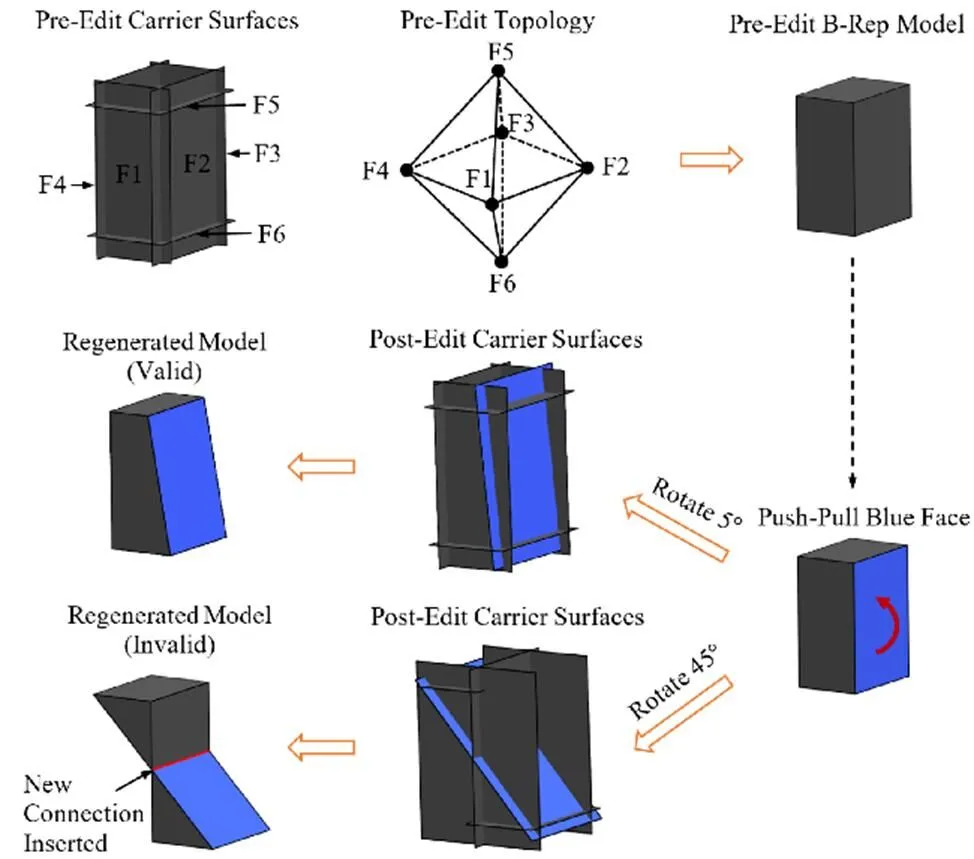
图14 直接建模中的协调更新问题[124]

在直接建模中，关键难点在于存在多个模型更新方案，有些不能给出有效的实体模型，有些虽然可以给出有效模型，但是不符合预期(与用户设计意图不一致)，一般而言，仅有一个方案是既能给出有效模型，又能与设计意图保持一致的，如图15所示。故而，直接建模的核心问题是方案决策问题(而参数化建模的核心问题是求解计算问题)。

图15 直接建模中的决策问题

针对这一问题，目前有2个思路：基于规则的以及基于连续性原理的。基于规则的方法[25,125-127]一般针对特定种类的实体模型和直接建模操作设计一组规则，来对模型进行更新。目前，这类方法已经可以鲁棒处理由平面组成的B-rep模型，但其他种类模型仍存在问题。基于连续性原理的方法[30,124]以模型更新时，其变动必须连续作为总要求，并将之转化成对几何元素的定量约束条件，从而实现对模型更新方案的系统决策。目前，这类方法已经可以鲁棒处理由平面和二次曲面组成的B-rep模型，但是尚不能处理含有自由曲面的B-rep模型。

总体而言，直接建模最核心的问题是对模型更新方案进行决策，其关键挑战在于决策方法的系统性，从而实现鲁棒的模型更新。当前的问题主要集中于[121,128]：

(1) 如何在直接编辑中保持设计语义(如边界面连接处的连续性)；

(2) 如何鲁棒地直接编辑带自由曲面的实体模型；

(3) 如何直接编辑参数化模型。

5 实体建模4.0 (未来发展)

实体建模的未来发展是多样的，此处仅能就某几个方面做出讨论，分别从新方法解决旧问题、新需求带来新问题、新技术带来新发展3个方面展开。

5.1 从支持详细设计到支持全过程设计——参数/直接融合建模

实体建模自诞生以来就一直被诟病为不能支撑全过程设计，仅对详细设计阶段有效，对概念设计阶段帮助不大[7]。人们往往只有在已经确定了设计细节后，才使用参数化CAD软件来建模[17,26-29]。直接建模带来了直观、任意的实体模型编辑能力，使其能够支撑概念设计。

然而，在目前的CAD系统中，参数化建模功能和直接建模功能是割裂的，分别支持详细设计阶段和概念设计阶段。如何无缝融合直接建模与参数化建模，解决长期以来大家期望的在一个统一的建模方法中同时支持概念设计和详细设计，是下一代CAD建模技术亟需解决的问题。

当前的融合方法尚无法达到无缝融合[129]。最常用的方法是以参数化建模为主干，将直接建模简单地当成一个特征加入到建模历史中，如图16(a)所示。这种基于“伪特征”的融合方法，会导致原设计语义的错乱或丢失，如图16(b)所示。理想的融合方法是基于直接建模操作重定义特征模型，实现模型中设计语义的智能维护，如图16(c)所示，如此，详细设计阶段的参数语义在概念设计阶段不会被直接建模操作所破坏。

图16 基于“伪特征”融合方法的缺陷((a)建模历史；(b)增大X的尺寸不会给出红圈中理想的模型更新，而是造成模型重生成失败，其原因在于边界面F2的丢失(见蓝圈中模型)；(c)无缝融合应该基于直接建模操作重定义被操作特征，实现参数模型中设计语义的智能维护)

参数/直接无缝融合的关键难点在于如何将旧的几何约束系统(代表设计语义)与直接建模作用后新的B-rep模型进行同步：直接建模作用后，CAD模型的边界表示(即B-rep模型)会发生变动，但是其建模历史(即特性信息，主要包括几何约束)仍保持不变，如此，计算机需要将B-rep模型的变动同步成为特性的变动(即需要更新特性信息以使得特征模型对应的B-rep模型和直接建模作用后的B-rep模型保持一致)。人们已经对此做了一些尝试[121,128]，其核心思想是将直接建模操作转译为特征重定义，比如几何约束增删、参数调整、特征调序等。这些方法在一些特定情形下取得了很好的结果，但在智能性和自动化程度上尚有很大进步空间。

5.2 从Computer-Aided Design 到Computer-Automated Design——复杂结构建模、设计、仿真与制造

3D打印(或增材制造)技术的快速发展使得制造具有复杂微观结构的产品成为可能，如图17所示。与传统实体建模中研究的复杂曲面完全不同，这种复杂结构在形状复杂度、数据规模量等方面发生了质的变化，对几何建模理论、几何表示数据结构、模型操作鲁棒性、自动化设计等方面都提出了新的需求，也带来了全新的问题。这将会给实体建模的基础理论和关键算法带来本质变化，主要包括：

(1) 实体的定义需要扩展。如前所述，传统实体概念所定义的对象是具有刚性、均质特性的产品，而复杂结构可能是刚性也可能是非刚性的(甚至是多模态的)，同时其还具有异质、多材料等特点。现有实体定义不能覆盖这些特点，需要被扩展以适用复杂结构。

(2) 复杂结构几何表示方法需要发展。复杂结构具有很高的“表面体积比”，这使得传统B-rep表示方法难以适用，否则将造成极大的存储消耗。如何实现复杂结构的轻量化表示，是当前复杂结构建模亟需解决的问题。目前的隐式表示[130]、参数表示[131]、图表示[132]、网格压缩表示[133]以及混合表示等方法都具有很大的局限性，往往只能处理特定类型的复杂结构[134]，与此同时，这些表示方法所能处理的结构复杂度仍非常有限，特别是难以处理如图17所示超复杂结构(这些结构如果以STL格式存储，将达到几百G存储量)。故而，发展新的统一高效复杂结构表示数据结构是当前需攻克的核心难题。

(3) 复杂结构自动设计方法需要发展。复杂结构的几何-性能-工艺具有强耦合的特点，这使得其难以像传统零件一样由人来设计，而是需要由计算机来自动设计，同时复杂结构所具有的丰富多样的几何细节，也让人工设计变得不可能。这些需求都促使工程设计从Computer-Aided Design向Computer-Automated Design发展。自动设计的关键问题落在CAD/CAE/CAM的一体化，旨在形成设计与性能和工艺仿真的自动化闭环，对CAD设计模型，通过CAE/CAM软件分析其性能和工艺，指导设计调整，反复迭代，达成设计目标，生成最优结构。形成这一自动化闭环的核心挑战在于CAD/CAE/CAM模型表示统一化[135]；然而，CAD模型面向制造和装配，CAE模型面向仿真计算，CAM模型面向工艺规划与控制，这三者的数据属性各不相同，但又互有重叠，故而设计一个既能满足设计、仿真、制造需求，又不重复存储数据，且不同属性数据能联动的产品表示数据结构是极具挑战的，即CAD/CAE/CAM统一模型表示需要满足三大极具挑战的要求：信息完整性、信息无冗余性、信息关联性。这方面的工作近年来进展很大，主要集中于结构优化(或称为拓扑优化、生成式设计，详见文献[136])，但是这些工作大多聚焦于CAD/CAE一体化，少数考虑CAM数据的工作也仅局限于简单工艺模型或约束[137]。

图17 简单、复杂、高度复杂结构实例[137-141]

5.3 智能CAD、云CAD

智能计算、云计算、并行计算以及虚拟现实等新一代计算技术将对CAD的发展有极大促进作用。

智能计算技术将推动CAD从设计师主导的人工建模向计算机主导的智能建模发展。通过机器学习，计算机将能够在一定程度上对设计师的设计、制造意图进行预测，从而实现对设计、制造语义的自动补全和识别，并将之转换为实体建模操作，这将极大地降低设计师的建模负担，尤其是在概念设计和工艺规划阶段。(本文中智能CAD的涵义并不包括下述功能：根据给定功能要求自动优化出产品形状或结构，这主要涉及机械式的优化算法，而非设计、制造意图的理解。)

虚拟现实技术、自然语言处理技术、计算机视觉技术将促使CAD系统从二维交互向三维智能交互发展，如通过手势、语言、草图来交互[142-145]，也会推动正、逆向设计的融合[146–150]。智能建模与智能交互相结合，正、逆向设计相互融合将极大提高产品设计的效率。然而值得一提的是，这一发展不要求实体建模基础理论和算法发生本质变化，更多的是在现有CAD技术基础上添加一层智能技术。

云计算带来了计算资源平台的变迁，这将使得CAD向“计算在云上而交互在本地”的模式发展。这一发展主要会带来2个需求：①快速“云-端”传输；②并行实体建模算法。其中，需求①显而易见，CAD建模的交互是实时的，故而云上的建模结果需要快速传输到本地，并作实时绘制。需求②的原因在于云CAD并不是简单将几何建模内核搬到云上，然后针对每个用户开一个建模线程(这种方式只是在套用云概念，和桌面CAD没有本质区别)，而是需要对用户操作(尤其是多人协同设计情况下，协同CAD系统的经典工作请参见文献[151])背后所调用的算法和资源进行管理、优化配置，合并相同类型计算，并行化不同类型计算，这本质上是要求实体建模算法向并行化发展。可以看出，云CAD和智能CAD不同，其对实体表示格式和操作算法都提出了本质变化要求。

另外，并行计算也能给实体建模中的一些老难题提供新思路。如，针对超大规模装配模型显示和编辑问题，并行计算可部分解决其中的效率问题。再如，针对实体建模鲁棒操作这个历史性难题，可以使用并行计算的高效率来换取曲面求交等计算的高精度，从而在一定程度上解决由计算误差带来的鲁棒性问题。传统上，需要在精度和效率之间平衡，进而造成不可控的计算误差。

6 总 结

本文对实体建模的发展历史作了简要梳理，按三段来介绍：早期实体建模基础理论与算法(50年代末到80年代末)，中期参数化建模(80年代末到2000年代末)，以及近期直接建模(2010年左右至今)。同时对各发展阶段的关键算法与难题以及其研究现状进行了讨论，对尚未形成系统解决方案的难题进行了重点评述。最后选取了3个方向对实体建模的未来做出展望。

值得注意的是，文中梳理的历史发展并不全面，仅涉及主要脉络。另外，未来展望也不全面，未来实体建模的发展必定是多样化而深刻的，特别是从Computer-Aided Design到Computer-Automated Design的发展趋势。这些发展也将给学术界和工业界带来众多有意义并且有趣的科研问题。

[1] COONS S, MANN R W. Computer-aided design related to the engineering design process[R]. Cambridge: M.I.T. Electronic Systems Laboratory, 1960.

[2] SHAH J, MÄNTYLÄ M. Parametric and feature-based CAD/CAM: concepts, techniques, and applications[EB/OL]. [2022-05-19]. https://www.researchgate.net/publication/44371716_Parametric_and_feature_based_CADCAM_concepts_techniques_and_applications_Jami_J_shah_Martti_Mantyla.

[3] COONS S A. An outline of the requirements for a computer-aided design system[C]//Proceedings of the Spring Joint Computer Conference. New York: ACM Press, 1963: 299-304.

[4] ROSS DT. Computer-aided design: a statement of objectives[R].Cambridge: Massachusetts Institute of Technology, 1960.

[5] REQUICHA A A G. GEOMETRIC MODELING : a First course 6-2, fundamental algorithms[R].Los Angeles: Univevsity of Southern California, 1999: 1-28.

[6] REQUICHA A A G. Representations for rigid solids: theory, methods, and systems[J]. ACM Computing Surveys, 1980, 12(4): 437-464.

[7] STAFF N A O E, COMPTON W D, ENGINEERING N A O. Design and Analysis of Integrated Manufacturing Systems[M]. Washington DC: National Academies Press, 1988: 167-199.

[8] SUTHERLAND I E. Sketchpad a man-machine graphical communication system[J]. SIMULATION, 1964, 2(5): R-3.

[9] REQUICHA A A G, VOELCKER H B. Solid modeling: current status and research directions[J]. IEEE Computer Graphics and Applications, 1983, 3(7): 25-37.

[10] BRAID I C. Geometric modelling[M]//Advances in computer graphics I. Berlin: Springer Berlin, 1986: 325-362.

[11] COHEN E, LYCHE T, RIESENFELD R F. MCAD: Key historical developments[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(5-8): 224-228.

[12] VOELCKER H B, REQUICHA A A G. Geometric modeling of mechanical parts and processes[J]. Computer, 1977, 10(12): 48-57.

[13] BRAID I C. The synthesis of solids bounded by many faces[J]. Communications of the ACM, 1975, 18(4): 209-216.

[14] SHAPIRO V. Solid modeling[M]//Handbook of computer aided geometric design. Amsterdam: Elsevier, 2002: 473-518.

[15] REQUICHA A A G. Constructive solid geometry[EB/OL]. [2022-06-19]. https://www.zhangqiaokeyan.com/ntis-science- repoort-thesis/020711454048.html.

[16] STROUD I. Boundary Representation Modelling Techniques[M]. London: Springer London, 2006.

[17] CAMBA J D, CONTERO M, COMPANY P. Parametric CAD modeling: an analysis of strategies for design reusability[J]. Computer-Aided Design, 2016, 74: 18-31.

[18] SHAH J J. Designing with Parametric CAD: classification and comparison of construction techniques[M]//Geometric modelling. Boston: Springer US, 2001: 53-68.

[19] HOFFMANN C M, JOAN-ARINYO R. Parametric modeling[M]//Handbook of computer aided geometric design. Amsterdam: Elsevier, 2002: 519-541.

[20] ROLLER D. An approach to computer-aided parametric design[J]. Computer-Aided Design, 1991, 23(5): 385-391.

[21] SHAH J J, ROGERS M T. Functional requirements and conceptual design of the Feature-Based Modelling System[J]. Computer-Aided Engineering Journal, 1988, 5(1): 9.

[22] SHAH J J, ANDERSON D, KIM Y S, et al. A discourse on geometric feature recognition from CAD models[J]. Journal of Computing and Information Science in Engineering, 2001, 1(1): 41-51.

[23] CAMBA J D, CONTERO M. Assessing the impact of geometric design intent annotations on parametric model alteration activities[J]. Computers in Industry, 2015, 71: 35-45.

[24] CHEN X P, HOFFMANN C M. On editability of feature-based design[J]. Computer-Aided Design, 1995, 27(12): 905-914.

[25] ROSSIGNAC J R. Issues on feature-based editing and interrogation of solid models[J]. Computers & Graphics, 1990, 14(2): 149-172.

[26] MONEDERO J. Parametric design: a review and some experiences[J]. Automation in Construction, 2000, 9(4): 369-377.

[27] ANDREWS P T J, SHAHIN T M M, SIVALOGANATHAN S. Design reuse in a CAD environment—four case studies[J]. Computers & Industrial Engineering, 1999, 37(1-2): 105-109.

[28] BETTIG B, BAPAT V, BHARADWAJ B. Limitations of parametric operators for supporting systematic design[C]// 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York: ASME, 2008: 131-142.

[29] BROWNP. CAD: do computers aid the design process after all?[J]. Intersect: The Stanford Journal of Science, Technology and Society, 2009, 2(1): 52-66.

[30] ZOU Q, FENG H Y. Push-pull direct modeling of solid CAD models[J]. Advances in Engineering Software, 2019, 127: 59-69.

[31] REQUICHA A A G. Mathematical models of rigid solid objects[EB/OL]. [2022-06-01]. https://www. zhangqiaokeyan. covn/ntis-science-report_other_thesis/020711446637.html.

[32] REQUICHA A A G. Representation of rigid solid objects[M]//Lecture notes in computer science. Berlin: Springer, 2006: 1-78.

[33] REQUICHA A A G, VOELCKER H B. Solid modeling: a historical summary and contemporary assessment[J]. IEEE Computer Graphics and Applications, 1982, 2(2): 9-24.

[34] MANTYLA M. A note on the modeling space of Euler operators[J]. Computer Vision, Graphics, and Image Processing, 1984, 26(1): 45-60.

[35] BAER A, EASTMAN C, HENRION M. Geometric modelling: a survey[J]. Computer-Aided Design, 1979, 11(5): 253-272.

[36] BOTSCH M, KOBBELT L, PAULY M, et al. Polygon Mesh Processing[M]. Wellesley: A K Peters, 2010: 1-250.

[37] JACOBSON A, KAVAN L, SORKINE-HORNUNG O. Robust inside-outside segmentation using generalized winding numbers[J]. ACM Transactions on Graphics, 2013, 32(4): 33.

[38] BRIDSON R, FEDKIW R, ANDERSON J. Robust treatment of collisions, contact and friction for cloth animation[C]// SIGGRAPH '05: ACM SIGGRAPH 2005 Courses. New York: ACM Press, 2005: 2-es.

[39] REQUICHA A A G, VOELCKER H B. Boolean operations in solid modeling: boundary evaluation and merging algorithms[J]. Proceedings of the IEEE, 1985, 73(1): 30-44.

[40] ROSSIGNAC J R, REQUICHA A A G. Offsetting operations in solid modelling[J]. Computer Aided Geometric Design, 1986, 3(2): 129-148.

[41] SHAPIRO V, VOSSLER D L. What is a parametric family of solids?[C]//The 3rd ACM Symposium on Solid Modeling and Applications. New York: ACM Press, 1995: 43-54.

[42] BODEIN Y, ROSE B, CAILLAUD E. Explicit reference modeling methodology in parametric CAD system[J]. Computers in Industry, 2014, 65(1): 136-147.

[43] BETTIG B, HOFFMANN C M. Geometric constraint solving in parametric computer-aided design[J]. Journal of Computing and Information Science in Engineering, 2011, 11(2): 1.

[44] BRAID I. Non-local blending of boundary models[J]. Computer-Aided Design, 1997, 29(2): 89-100.

[45] GRAYER A R. Alternative approaches in geometric modelling[J]. Computer-Aided Design, 1980, 12(4): 189-192.

[46] Michelucci D. An Introduction to the Robustness Issue[EB/OL]. [2022-05-21]. https://ufrsciencestech.u-bourgo gne.fr/master/mil-tc5/tmp/PAPERS/cadcam-swiss.pdf.

[47] HOFFMANN C M. Robustness in geometric computations[J]. Journal of Computing and Information Science in Engineering, 2001, 1(2): 143-155.

[48] ROSSIGNAC J R. Through the cracks of the solid modeling milestone[M]//From object modelling to advanced visual communication. Heidelberg: Springer, 1994: 1-75.

[49] HU C Y, PATRIKALAKIS N M, YE X Z. Robust interval solid modelling Part I: representations[J]. Computer-Aided Design, 1996, 28(10): 807-817.

[50] ZOU Q, FENG H Y. Push-pull direct modeling of solid CAD models[J]. Advances in Engineering Software, 2019, 127: 59-69.

[51] SHEN G L, SAKKALIS T, PATRIKALAKIS N. Analysis of boundary representation model rectification[C]//The 6th ACM Symposium on Solid Modeling and Applications. New York: ACM Press, 2001: 149-158.

[52] BERBERICH E, EIGENWILLIG A, HEMMER M, et al. Exacus: efficient and exact algorithms for curves and surfaces[M]//Algorithms - ESA 2005. Berlin: Springer, 2005: 155-166.

[53] KEYSER J, CULVER T, FOSKEY M, et al. ESOLID—a system for exact boundary evaluation[J]. Computer-Aided Design, 2004, 36(2): 175-193.

[54] BENOUAMER M, MICHELUCCI D, PÉROCHE B. Error-free boundary evaluation using lazy rational arithmetic: a detailed implementation[M]. New York: ACM Press, 1993: 115-26.

[55] TRETTNER P, NEHRING-WIRXEL J, KOBBELT L. EMBER: exact mesh booleans via efficient & robust local arrangements[J]. ACM Transactions on Graphics, 2022, 41(4): 39.

[56] WANG C C L, MANOCHA D. Efficient boundary extraction of BSP solids based on clipping operations[J]. IEEE Transactions on Visualization and Computer Graphics, 2013, 19(1): 16-29.

[57] BERNSTEIN G, FUSSELL D. Fast, exact, linear booleans[J]. Computer Graphics Forum, 2009, 28(5): 1269-1278.

[58] JACKSON D J. Boundary representation modelling with local tolerances[C]//The 3rd ACM Symposium on Solid Modeling and Applications. New York: ACM Press, 1995: 247-254.

[59] STROUD I, NAGY H. Solid modeling and CAD systems : how to survive a CAD system[EB/OL]. [2022-06-10]. https://www. researchgate.net/publication/267018694_solid_modelling_and_CAD_systems_How_to_survive_a_CAD_system.

[60] QI J C, SHAPIRO V. ε-Topological formulation of tolerant solid modeling[J]. Computer-Aided Design, 2006, 38(4): 367-377.

[61] ROSSIGNAC J R. Constraints in constructive solid geometry[C]//1986 Workshop on Interactive 3D graphics. New York: ACM Press, 1987: 93-110.

[62] MUN D, HAN S, KIM J, et al. A set of standard modeling commands for the history-based parametric approach[J]. Computer-Aided Design, 2003, 35(13): 1171-1179.

[63] HOFFMANN C M, JOAN-ARINYO R. On user-defined features[J]. Computer-Aided Design, 1998, 30(5): 321-332.

[64] BETTIG B, SHAH J. Derivation of a standard set of geometric constraints for parametric modeling and data exchange[J]. Computer-Aided Design, 2001, 33(1): 17-33.

[65] BIDARRA R, BRONSVOORT W F. Semantic feature modelling[J]. Computer-Aided Design, 2000, 32(3): 201-225.

[66] LI L, ZHENG Y F, YANG M L, et al. A survey of feature modeling methods: historical evolution and new development[J]. Robotics and Computer-Integrated Manufacturing, 2020, 61: 101851.

[67] HOFFMANN C M. On the semantics of generative geometry representations[C]//1993 Design Technical Conferences. New York: ASME, 2021: 411-419.

[68] MARCHEIX D, PIERRA G. A survey of the persistent Naming problem[C]//The 7th ACM Symposium on Solid Modeling and Applications. New York: ACM Press, 2002: 13-22.

[69] FARJANA S H, HAN S. Mechanisms of persistent identification of topological entities in CAD systems: a review[J]. Alexandria Engineering Journal, 2018, 57(4): 2837-2849.

[70] CAPOYLEAS V, CHEN X P, M HOFFMANN C. Generic Naming in generative, constraint-based design[J]. Computer- Aided Design, 1996, 28(1): 17-26.

[71] WANG Y, NNAJI B O. Geometry-based semantic ID for persistent and interoperable reference in feature-based parametric modeling[J]. Computer-Aided Design, 2005, 37(10): 1081-1093.

[72] BABA-ALI M, MARCHEIX D, SKAPIN X. A method to improve matching process by shape characteristics in parametric systems[J]. Computer-Aided Design and Applications, 2009, 6(3): 341-350.

[73] KRIPAC J. A mechanism for persistently Naming topological entities in history-based parametric solid models[J]. Computer-Aided Design, 1997, 29(2): 113-122.

[74] AGBODAN D, MARCHEIX D, PIERRA G, et al. A topological entity matching technique for geometric parametric models[C]//2003 Shape Modeling International. New York: IEEE Press, 2003: 235-244.

[75] WU J J, ZHANG T B, ZHANG X F, et al. A face based mechanism for Naming, recording and retrieving topological entities[J]. Computer-Aided Design, 2001, 33(10): 687-698.

[76] MUN D W, HAN S H. Identification of topological entities and Naming mapping for parametric CAD model exchanges[J]. International Journal of CAD/CAM, 2005, 5(1): 69-81.

[77] CHEON S U, MUN D, HAN S, et al. Name matching method using topology merging and splitting history for exchange of feature-based CAD models[J]. Journal of Mechanical Science and Technology, 2012, 26(10): 3201-3212.

[78] FARJANA S H, HAN S, MUN D. Implementation of persistent identification of topological entities based on macro-parametrics approach[J]. Journal of Computational Design and Engineering, 2016, 3(2): 161-177.

[79] RAGHOTHAMA S, SHAPIRO V. Boundary representation deformation in parametric solid modeling[J]. ACM Transactions on Graphics, 1998, 17(4): 259-286.

[80] RAGHOTHAMA S, SHAPIRO V. Topological framework for part families[J]. Journal of Computing and Information Science in Engineering, 2002, 2(4): 246-255.

[81] RAGHOTHAMA S, SHAPIRO V. Necessary conditions for boundary representation variance[C]//The 13th Annual Symposium on Computational Geometry. New York: ACM Press, 1997: 77-86.

[82] MARTIN K, WANG W P. Geometric modeling and processing 2000. Theory and applications[M]. New York: IEEE Press, 2002: 1-4.

[83] BIDARRA R, NYIRENDA P J, BRONSVOORT W F. A feature-based solution to the persistent Naming problem[J]. Computer-Aided Design and Applications, 2005, 2(1-4): 517-526.

[84] VAN DER MEIDEN H A, BRONSVOORT W F. Tracking topological changes in parametric models[J]. Computer Aided Geometric Design, 2010, 27(3): 281-293.

[85] HOFFMANN C M, KIM K J. Towards valid parametric CAD models[J]. Computer-Aided Design, 2001, 33(1): 81-90.

[86] TANG Z H, ZOU Q, GAO S M. Towards computing complete parameter ranges in parametric modeling[EB/OL]. [2022-05-19]. https://arxiv.org/abs/2206.08698.

[87] HOFFMAN C M, LOMONOSOV A, SITHARAM M. Decomposition plans for geometric constraint problems, part II: new algorithms[J]. Journal of Symbolic Computation, 2001, 31(4): 409-427.

[88] ZOU Q, TANG Z H, FENG H Y, et al. A review on geometric constraint solving[EB/OL]. [2022-04-21]. https://arxiv.org/ abs/2202.13795.

[89] DUFOURD J F, MATHIS P, SCHRECK P. Geometric construction by assembling solved subfigures[J]. Artificial Intelligence, 1998, 99(1): 73-119.

[90] JOAN-ARINYO R, SOTO A. A correct rule-based geometric constraint solver[J]. Computers & Graphics, 1997, 21(5): 599-609.

[91] OWEN J C. Algebraic solution for geometry from dimensional constraints[C]//The 1st ACM Symposium on Solid Modeling Foundations and CAD/CAM Applications. New York: ACM Press, 1991: 397-407.

[92] BOUMA W, FUDOS I, HOFFMANN C, et al. Geometric constraint solver[J]. Computer-Aided Design, 1995, 27(6): 487-501.

[93] FUDOS I, HOFFMANN C M. A graph-constructive approach to solving systems of geometric constraints[J]. ACM Transactions on Graphics, 1997, 16(2): 179-216.

[94] GAO X S, HOFFMANN C M, YANG W Q. Solving spatial basic geometric constraint configurations with locus intersection[C]//The 7th ACM Symposium on Solid Modeling and Applications. New York: ACM Press, 2002: 95-104.

[95] BARDORD L A. A graphical, language-based editor for generic solid models represented by constraints[M]. Ithaca: Cornell University, 1987.

[96] SERRANO D. Constraint management in conceptual design[EB/OL]. [2022-06-29]. https://www.researchgate.net/ publication/243764572_Constraints_in_conceptual_design.

[97] AIT-AOUDIA S, JEGOU R, MICHELUCCI D. Reduction of constraint systems[EB/OL]. [2022-05-17]. https://arxiv.org/ abs/1405.6131.

[98] LATHAM R S, MIDDLEDITCH A E. Connectivity analysis: a tool for processing geometric constraints[J]. Computer-Aided Design, 1996, 28(11): 917-928.

[99] HOFFMANN C M, LOMONOSOV A, SITHARAM M. Finding solvable subsets of constraint graphs[M]//Principles and practice of constraint programming-CP97. Berlin: Springer, 1997: 463-477.

[100]HIDALGO M, JOAN-ARINYO R. H-graphs: a new representation for tree decompositions of graphs[J]. Computer-Aided Design, 2015, 67-68: 38-47.

[101]GAO X S, LIN Q, ZHANG G F. A C-tree decomposition algorithm for 2D and 3D geometric constraint solving[J]. Computer-Aided Design, 2006, 38(1): 1-13.

[102]XIA H J, WANG B X, CHEN L P, et al. 3D geometric constraint solving using the method of kinematic analysis[J]. The International Journal of Advanced Manufacturing Technology, 2008, 35(7): 711-722.

[103]MICHELUCCI D, FOUFOU S. Geometric constraint solving: the witness configuration method[J]. Computer-Aided Design, 2006, 38(4): 284-299.

[104]KUBICKI A, MICHELUCCI D, FOUFOU S. Witness computation for solving geometric constraint systems[C]//2014 Science and Information Conference. New York: IEEE Press, 2014: 759-770.

[105]THIERRY S E B, SCHRECK P, MICHELUCCI D, et al. Extensions of the witness method to characterize under-, over- and well-constrained geometric constraint systems[J]. Computer-Aided Design, 2011, 43(10): 1234-1249.

[106]FOUFOU S, MICHELUCCI D. Interrogating witnesses for geometric constraint solving[J]. Information and Computation, 2012, 216: 24-38.

[107]MOINET M, MANDIL G, SERRE P. Defining tools to address over-constrained geometric problems in computer aided design[J]. Computer-Aided Design, 2014, 48: 42-52.

[108]HU H, KLEINER M, PERNOT J P. Over-constraints detection and resolution in geometric equation systems[J]. Computer- Aided Design, 2017, 90: 84-94.

[109]ZOU Q, FENG H Y. On limitations of the witness configuration method for geometric constraint solving in CAD modeling[EB/OL]. [2022-05-15]. https://arxiv.org/abs/1904. 00526.

[110]HALLER K, LEE-ST JOHN A, SITHARAM M, et al. Body-and-cad geometric constraint systems[J]. Computational Geometry, 2012, 45(8): 385-405.

[111]HU H, KLEINER M, PERNOT J P, et al. Correction to: geometric over-constraints detection: a survey[J]. Archives of Computational Methods in Engineering, 2021, 28(7): 5037.

[112]JERMANN C, HOSOBE H. A constraint hierarchies approach to geometric constraints on sketches[C]//2008 ACM Symposium on Applied Computing. New York: ACM Press, 2008: 1843-1844.

[113]BORNING A, FREEMAN-BENSON B, WILSON M. Constraint hierarchies[J]. LISP and Symbolic Computation, 1992, 5(3): 223-270.

[114]JOAN-ARINYO R, SOTO-RIERA A, VILA-MARTA S, et al. Transforming an under-constrained geometric constraint problem into a well-constrained one[C]//The 8th ACM Symposium on Solid Modeling and Applications. New York: ACM Press, 2003: 33-44.

[115]HOFFMANN C M, SITHARAM M, YUAN B. Making constraint solvers more usable: overconstraint problem[J]. Computer-Aided Design, 2004, 36(4): 377-399.

[116]ZHANG G F, GAO X S. Well-constrained completion and decomposition for under-constrained geometric constraint problems[J]. International Journal of Computational Geometry & Applications, 2006, 16(5/6): 461-478.

[117]MURUGAPPAN S, SELLAMANI S, RAMANI K. Towards beautification of freehand sketches using suggestions[C]//The 6th Eurographics Symposium on Sketch-Based Interfaces and Modeling. New York: ACM Press, 2009: 69-76.

[118]MILLS B I, LANGBEIN F C, MARSHALL A D, et al. Estimate of frequencies of geometric regularities for use in reverse engineering of simple mechanical components[EB/OL]. [2022-06-15]. https://www.researchgate.net/publication/20001 8274_Estimate_of_Frequencies_of_Geometric_Regularities_for_use_in_Reverse_Engineering_of_Simple_Mechanical_Components?channel=doi&linkld=0912f50b8c3cbzea23000000&showFulltes=true.

[119]ZOU H L, LEE Y T. Constraint-based beautification and dimensioning of 3D polyhedral models reconstructed from 2D sketches[J]. Computer-Aided Design, 2007, 39(11): 1025-1036.

[120]LANGBEIN F C, MARSHALL A D, MARTIN R R. Choosing consistent constraints for beautification of reverse engineered geometric models[J]. Computer-Aided Design, 2004, 36(3): 261-278.

[121]ZOU Q, FENG H Y. A decision-support method for information inconsistency resolution in direct modeling of CAD models[J]. Advanced Engineering Informatics, 2020, 44: 101087.

[122]STROUD I, XIROUCHAKIS P C. CAGD—computer-aided gravestone design[J]. Advances in Engineering Software, 2006, 37(5): 277-286.

[123]FAHLBUSCH K-P, ROSER TD. HP PE/SolidDesigner: dynamic modeling for three-dimensional computer-aided design[J]. Hewlett-Packard Journal, 1995, 46: 6-13.

[124]ZOU Q, FENG H Y. A robust direct modeling method for quadric B-rep models based on geometry–topology inconsistency tracking[J]. Engineering With Computers, 2022, 38(4): 3815-3830.

[125]WOO Y, LEE S H. Volumetric modification of solid CAD models independent of design features[J]. Advances in Engineering Software, 2006, 37(12): 826-835.

[126]KIM BC, Mun DW. Stepwise volume decomposition for the modification of B-rep models[J]. The International Journal of Advanced Manufacturing Technology, 2014, 75: 1393-403.

[127]FU J, CHEN X, GAO S M. Automatic synchronization of a feature model with direct editing based on cellular model[J]. Computer-Aided Design and Applications, 2017, 14(5): 680-692.

[128]QIN X L, TANG Z H, GAO S M. Automatic update of feature model after direct modeling operation[J]. Computer-Aided Design and Applications, 2020, 18(1): 170-185.

[129]ZOU Q. Parametric/direct CAD integration[EB/OL]. [2022- 05-17]. https://arxiv.org/abs/2203.02252.

[130]DING J H, ZOU Q, QU S, et al. STL-free design and manufacturing paradigm for high-precision powder bed fusion[J]. CIRP Annals, 2021, 70(1): 167-170.

[131]MASSARWI F, MACHCHHAR J, ANTOLIN P, et al. Hierarchical, random and bifurcation tiling with heterogeneity in micro-structures construction via functional composition[J]. Computer-Aided Design, 2018, 102: 148-159.

[132]GUPTA A, ALLEN G, ROSSIGNAC J. QUADOR: QUADric-of-revolution beams for lattices[J]. Computer-Aided Design, 2018, 102: 160-170.

[133]CHOUGRANI L, PERNOT J P, VÉRON P, et al. Lattice structure lightweight triangulation for additive manufacturing[J]. Computer-Aided Design, 2017, 90: 95-104.

[134]DONG G Y, TANG Y L, ZHAO Y F. A survey of modeling of lattice structures fabricated by additive manufacturing[J]. Journal of Mechanical Design, 2017, 139(10): 100906.

[135]SHAPIRO V, TSUKANOV I, GRISHIN A. Geometric issues in computer aided design/computer aided engineering integration[J]. Journal of Computing and Information Science in Engineering, 2011, 11(2): 1.

[136]WU J, SIGMUND O, GROEN J P. Topology optimization of multi-scale structures: a review[J].Structural and Multidisciplinary Optimization, 2021, 63(3): 1455-1480.

[137]DING J H, ZOU Q, QU S, et al. STL-free design and manufacturing paradigm for high-precision powder bed fusion[J]. CIRP Annals, 2021, 70(1): 167-170.

[138]LIU S J, LIU T, ZOU Q, et al. Memory-efficient modeling and slicing of large-scale adaptive lattice structures[J]. Journal of Computing and Information Science in Engineering, 2021: 1-16.

[139]GUPTA A, ALLEN G, ROSSIGNAC J. QUADOR: QUADric- of-revolution beams for lattices[J]. Computer-Aided Design, 2018, 102: 160-170.

[140]MASSARWI F, MACHCHHAR J, ANTOLIN P, et al. Hierarchical, random and bifurcation tiling with heterogeneity in micro-structures construction via functional composition[J]. Computer-Aided Design, 2018, 102: 148-159.

[141]LIU S J, LIU T, ZOU Q, et al. Memory-efficient modeling and slicing of large-scale adaptive lattice structures[J]. Journal of Computing and Information Science in Engineering, 2021: 1-16.

[142]LI C J, PAN H, BOUSSEAU A, et al. Free2CAD: parsing freehand drawings into CAD commands[J]. ACM Transactions on Graphics, 2022, 41(4): 93.

[143]LI C J, PAN H, BOUSSEAU A, et al. Sketch2CAD: sequential CAD modeling by sketching in context[J]. ACM Transactions on Graphics, 2020, 39(6): 164.

[144]SEFF A, ZHOU W D, RICHARDSON N, et al. Vitruvion: a generative model of parametric CAD sketches[EB/OL]. [2022-05-30]. https://arxiv.org/abs/2109.14124.

[145]GANIN Y, BARTUNOV S, LI Y N, et al. Computer-aided design as language[M]//Advances in neural information processing systems 2021. Cambridge: MIT Press, 2021: 5885-5897.

[146]UY M A, CHANG Y, SUNG M, et al. Point2Cyl: reverse engineering 3D objects from point clouds to extrusion cylinders[C]//2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2022: 11840-11850.

[147]GUO H X, LIU S L, PAN H, et al. ComplexGen: CAD reconstruction by B-rep chain complex generation[EB/OL]. [2022-05-18]. https://arxiv.org/abs/2205.1457.

[148]WU R D, XIAO C, ZHENG C X. DeepCAD: a deep generative network for computer-aided design models[C]//2021 IEEE/CVF International Conference on Computer Vision. New York: IEEE Press, 2022: 6752-6762.

[149]XU X H, PENG W Z, CHENG C Y, et al. Inferring CAD modeling sequences using zone graphs[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2021: 6058-6066.

[150]LAMBOURNE J G, WILLIS K D D, JAYARAMAN P K, et al. BRepNet: a topological message passing system for solid models[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2021: 12768-12777.

[151]LI M, GAO S M, WANG C C L. Real-time collaborative design with heterogeneous CAD systems based on neutral modeling commands[J]. Journal of Computing and Information Science in Engineering, 2007, 7(2): 113-125.

[152]EASTMAN C M, WEILER K J. Geometric modeling using the Euler operators[R]. Pittsburgh: Carnegie Mellon University; 1979.

A note on solid modeling: history, state of the art, future

ZOU Qiang

(State Key Lab of CAD&CG, Zhejiang University, Hangzhou Zhejiang 310027, China)

Solid modeling is a technique underlying CAD software as we see it today, and its theories and algorithms are among the most fundamental milestones in the historical development of CAD. Basically, it has answered the question of what geometric information a computer should store and how to store/manipulate them in order for the computer to aid the processes of design and manufacturing. This paper provides abrief review on the historical development of solid modeling, its fundamental research problems, as well as their challenges and state of the art. It then concludes with three prospective trends of solid modeling, especially the promising paradigm shift from “Computer-Aided Design” to “Computer-Automated Design”.

CAD; geometric modeling; solid modeling; parametric modeling; direct modeling; structure modeling; intelligent CAD

TP 391

10.11996/JG.j.2095-302X.2022060987

A

2095-302X(2022)06-0987-15

2022-07-31；

：2022-10-12

国家自然科学基金项目(62102355)；浙江省自然科学基金项目(LQ22F020012)

邹 强(1990-)，男，研究员，博士。主要研究方向为CAD。E-mail：qiangzou@cad.zju.edu.cn

31 July，2022；

12 October，2022

National Natural Science Foundation of China (62102355), Natural Science Foundation of Zhejiang Province (LQ22F020012)

ZOU Qiang (1990-), professor, Ph.D. His main research interest covers CAD. E-mail：qiangzou@cad.zju.edu.cn