Nesbitt不等式的一个新推广及引申
2023-01-12 07:27山东省邹平双语学校256200
中学数学研究(江西) 2023年1期
山东省邹平双语学校 (256200)
姜坤崇 高奇媚

这是一个对称、简洁、优美、内涵丰富、应用广泛的经典不等式,历史上曾作为1963年莫斯科数学竞赛题出现过,对它的研究(如证法、推广、加强、加细、应用等)也历久不衰,文献[1]给出了它的一种新推广,本文给出它的一种新推广.

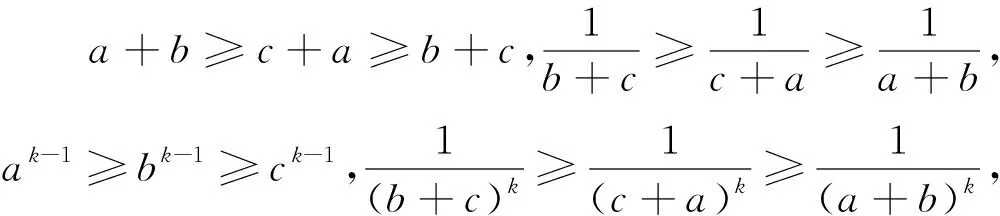
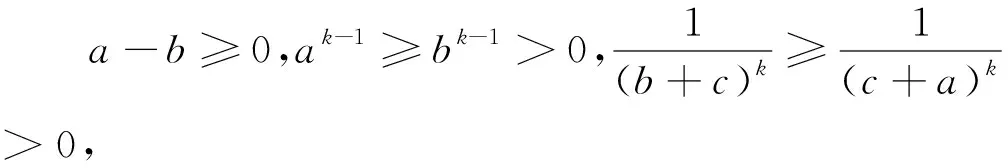
在不等式②中令k=1即得不等式①,所以不等式②为不等式①的一种推广.
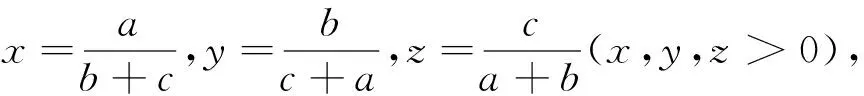
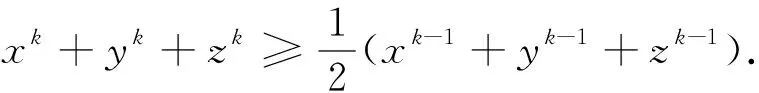
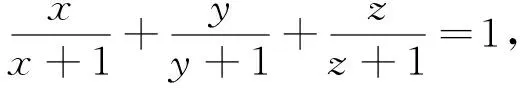

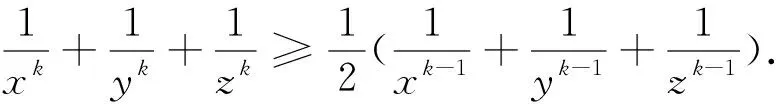
命题1中的不等式②是关于三个正数a,b,c的不等式,若将它推广为n(n≥3)个正数的不等式,则有如下命题4成立.
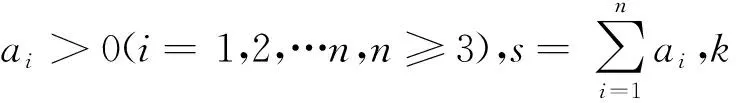
证明从略.
同样的,命题2、3中的不等式也可以推广到n(n≥3)个正数中去,有如下的两个命题成立.
命题5 设xi>0(i=1,2,…,n,n≥3),且
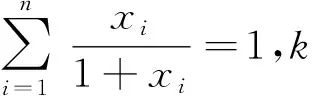
命题6 设xi>0(i=1,2,…,n,n≥3),且

以上两个命题的证明均从略.
由命题1,我们可得一个有趣的无穷长的代数不等式链:

同样,由命题2、3可分别得另两个无穷长的条件不等式链:
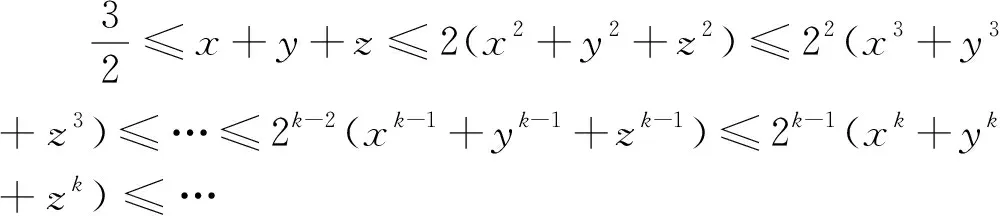

由命题8、9,我们也可得任意多的特例不等式.由命题4、5、6我们也可以分别得到无穷长的不等式链和无穷多的特例不等式,限于篇幅,这里不再给出.
猜你喜欢
中等数学(2022年4期)2022-08-29
中学数学研究(广东)(2022年1期)2022-03-14
儿童时代·快乐苗苗(2021年11期)2022-01-22
学校教育研究(2021年2期)2021-02-08
中等数学(2020年7期)2020-11-26
中等数学(2020年4期)2020-08-24
河北理科教学研究(2020年4期)2020-01-17
中等数学(2019年5期)2019-08-30
中学生英语·教师版(2019年12期)2019-08-03
廉政瞭望(2012年1期)2012-02-11

