初中物理课堂中图形结合的解题方法分析

张丽燕

(江苏省如东县茗海中学 226406)

在初中物理的学习中，学生解题能力的发展不是一蹴而就的，是学生综合运用所学物理学科知识，在逻辑思维、抽象思维等高阶思维支持下进行有效思考和推理论证等学习活动，并保证可以顺利完成相应物理问题求解任务.然而，解题能力的培养讲究技巧性，单纯从“量”的层面上进行解题训练是远远不够的，必须要注重传授给学生图形结合法等有价值有效的解题思想与方法，配合典型例题的解题训练，持续提高初中生自身的物理解题能力.

1 图形结合法及其在初中物理解题中应用价值

图形结合法实际上是相较于数形结合思想而言的一种有效解题法和思维方式，主要是结合物理问题中的题干信息与条件，将繁杂、抽象的物理分析过程或问题呈现方式以直观的图像形式展现出来，保证学生通过“观图”的方式来简化物理问题求解过程，降低学生思考及解题难度.特别是在碰到那些涉及到隐蔽解题条件或过大文字信息量的物理问题，为了简化相应的问题求解流程，降低学生分析问题的难度，可以采取画图的方式来具象化这些文字信息，保证相关信息以更加简化的方式展现出来，避免过多无用解题信息干扰学生顺利求解物理问题.图形结合法在物理问题求解中的融入，实际上源于数学领域中数形结合思想的应用，所谓的数形结合是指促使数与形二者之间形成等价转换的方式，来持续性简化物理问题求解的过程，帮助他们快速找到解决物理问题的突破口.因为在图形的支持下，可以促使学生更好结合形象思维与抽象思维，极大简化了繁杂的物理问题，对优化初中生物理解题思路，提高物理解题能力有很大帮助.比如，在遇到那些涉及到大量文字表述的物理问题期间，如果其中文字描述过于抽象，关系错综复杂，那么此时在对其进行求解时，可以灵活地应用图形结合法，以直观图形或图象的方式来展示有关繁杂、抽象的文字类物理问题题干信息，保证可以借助图形结合法的创新运用来辅助初中生对物理问题中的关键解题条件、解题信息等进行理解，并最终通过深入分析问题来形成正确的解题思路.

2 图形结合法及其在初中物理解题中应用策略

2.1 培养图形结合解题意识

在指导学生学习图形结合法来求解物理问题期间，首先需要抓住平时教学时机或解题训练时机，有计划地培养及强化他们的图形结合解题意识，助力他们运用图形结合法解决物理问题的良好习惯养成.特别是可以在学生运用常规解题法对物理问题求解过程中，如果无法快速确定解题的突破口与思路，那么可以指导他们亲自动手进行绘图，在画一画的过程中将相关物理问题信息及条件直观地进行表达.在学生利用这种画图的方式求解物理问题之后，可以使他们切实意识到图形结合法求解物理问题的重要价值，这样可以培养及强化他们的图形结合解题意识，对他们解题能力的培养有很大帮助.但是这种图形结合解题意识的培养不是一蹴而就的，必须要注意结合物理学科的基本教学要求和规定，采用绘图法进行绘图，同时借助图形结合解题意识指导他们逐步掌握利用绘图的方式来辅助自己审题，最终可以使他们在后续的物理问题分析或求解中，巧用画图的方式进行问题求解.

例1在某一水平地面上搁置有一木块B，之后在其上面搁置木块A，那么下列说法准确的为( ).

A.木块A的重力和木块B对木块A的支持力二者为一对平衡力

B.木块B的重力和地面对木块B的支持力二者为一对平衡力

C.木块A对木块B的压力和木块B对木块A的支持力二者为一对平衡力

D.木块A的重力和地面对木块B的支持力二者为一对相互作用力

解析本题是一道考查学生对相互作用力、平衡力方面物理知识理解情况的类型题，二者相同点主要表现为力的大小保持相等状态，并且力的方向保持相反状态.而它们的不同之处是平衡力相应地作用于同一个物体上面，而相互作用力则是作用在两个物体上面.只有初中生对相关的物理概念形成正确认知，并且在实际的问题分析中可以对不同受力状态进行点评，那么才能够对各个选项的正误进行判断.然而，如果学生在分析木块A和B所受力的情况中仅仅依靠文字描述或头脑想象的方式，那么学生很难形成深刻认知，最终得到的结果也可能不正确.但是如果可以指导学生在求解本道选择题的过程中，根据选项中各个给出的力，相应地绘制出对应的受力分析图，那么就可以帮助他们快速判断这些选项的正误.在这种基于图形结合的解题思路支持下，可以帮助他们快速确定本道题的正确解决答案是选项A.

2.2 结合他法用图形结合法

实际上不存在任何一种万能解题法，图形结合解题法虽然有效，但是同样不是万能解题法，因为图形结合法在物理问题求解中的应用，更多的是起到辅助初中生开展审题的一个关键解题环节.而学生能否顺利找到物理问题解题的突破口，除了要求他们通过认真审题来搞清解题条件和信息外，还需要在解题中对自己得到的解题思路进行认真梳理，保证可以找到能够准确求解物理问题的最终解题方法与思路.而基于图形结合解题法的应用，可以使学生在审题过程中挖掘出非常有价值的解题条件与信息，之后可以灵活地运用反推法等一些其他解题法来帮助他们对整个解题过程进行认真梳理，保证可以通过综合应用图形结合法同其他解题法来快速确定物理问题的最佳解题思路.而反推法实际上就是一种基于物理问题结论视角来反推的分析法，该法在物理问题求解中的灵活应用可以增强学生解题的严密性，避免学生混淆已知的有效条件和无效的解题信息，排除外在因素的干扰，对提高他们解题准确度有很大帮助.

例2 如图1，某一电路电源电压E是6V，其中R为一定值电阻，阻值为20Ω，现在闭合开关，试求：

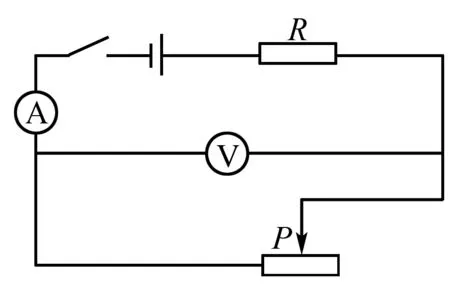
图1

(1)在V表示数是3V的时候，此时滑动变阻器的有效接入电阻是多少？

(2)在滑动变阻器接入电路的有效电阻值达到10Ω的情况下，R的对应功率是多少？

解析本道物理题是一道非常典型的电学问题，为了帮助学生简化问题求解过程，降低他们解题难度，可以采取图形结合解题法来帮助他们认真审题，助力他们高效地学习相关物理知识，具体的审题法表现如下：

其一，基于问题(1)，可以基于图形结合解题法来绘制出图1所示的等效电路图的有效解题部分(图2)，并且可以在其中标识出题干给出的已知量与未知量，以及统一相应的单位，这样可以帮助他们快速简化整个问题求解过程，提高了解题准确度.

图2 图3

其二，针对问题(2)的求解，也可以基于图形结合解题方法来绘制出图3所示的有效解题部分，保证可以在对各种关键解题中所涉及的物理量进行确定基础上，快速列式求解问题.

其三，在利用图形结合解题法对本道题中的问题(1)和(2)的求解过程进行有效梳理的基础上，可以继续指导他们创新运用反推法，来对整个物理问题求解过程中涉及到的解题思路进行有效梳理.比如，针对图2而言，可以结合相应等效电路图，给出U2=3V，求解R2=？这一求解思路，之后可以在这种等效电路图的支持下，反推出相应的解题思路与条件，最终可以通过欧姆定律来对I2进行求解，结合串联电路电流保持一致特性来确定I1.鉴于R1=20Ω，可以首先求解U1，之后结合串联电路电压的相应关系，求出U1=U总-U2，经过反推认真梳理问题求解思路，对提高学生解题准确度与效率有很大帮助.

2.3 基于图形结合强化训练

为了使初中生熟练掌握图形结合解题法，并且可以将其应用于解决物理问题，单纯依靠口授的方式或者纸上谈兵的方式，传授给学生图形结合法解题方法，会直接影响物理问题的顺利求解.只有通过反复参与解题训练，反复运用图形结合解题法求解物理问题，才能在这种反复解题训练实践过程中有效锻炼他们自身的解题能力.因此，在开展物理解题教学中，教师可以有计划地为学生选择一些典型的物理问题，并指导学生利用图形结合方法来对这些问题进行求解，这样就可以在反复用图形结合解题方法的过程中，有效锻炼及发展学生自身的问题求解能力.

例3现有两个阻值各不相同的电阻R1和R2，通过它们的电流会伴随着电压的改变而相应形成的电压电流变化图像(I-U图象)均表现为一次函数.在图4中R图线中主要涵盖了三个区域，对R1和R2二者进行串联或并联之后所形成的电路电阻相应地表现为R串和R并，并且它们对应的R曲线图(I-U图线)本身应该处于的区域应该在图4的哪个区域呢？

图4 图5

解析本道题是一道电力学方面的问题，整体的问题求解中涉及到图线，并且涉及到R、I和U等较多的抽象性比较强的物理参数，所以初中生分析问题的难度比较大，并且容易造成错解问题，整体解题难度比较大.但是如果可以指导学生在分析及求解问题的过程中可以灵活地融合图形结合解题法，那么可以帮助他们简化整个问题的求解过程.

如图5，作出一个平行于I轴的直线同U轴相较于U0，对应R1和R2阻值的电流分别是I1和I2，并且R线本身如果具有越大的斜率，那么对应I值也会更大.在图5给出的3个区域中，区域①涉及到最大电阻值，区域②次之，而区域③的电阻值最小.假定可以将两个电阻进行串联，那么可知R串处于区域①，并且这时候相应值比R1和R2阻值都大；假定对R1和R2阻值进行并联，那么可以确定R并本身处于区域③之中，并且该值要比R1和R2阻值都小.由此可见，基于图形结合解题法的运用，可以使学生在分析抽象性问题过程中更好地对自己的解题思路进行确定，简化了整个物理问题求解过程，求解难度也大大降低，非常有利于助力学生解题能力发展.

总之，图形结合法是助力初中生物理解题能力提升的一个有效解题方法.在平时物理教学中，教师要注意将图形结合法有效地贯穿于学生学习、解题训练等不同环节中，还要为他们提供一些典型物理问题，来强化他们使用图形结合解题法的运用能力，不断提高学生的物理解题能力.