浅谈在课堂教学中如何渗透方程与函数思想

倪行舟

(福建省福清市海口中学 350300)

对于数学教学来说，培养学生建模思想贯穿于整个初中数学教学的始终，是学习、理解和运用数学知识的重要手段.《数学课程标准》指出：“引导学生在实践场景当中对数学问题进行剥离，创建相应的数学模型，寻求数学问题的结果，进而对数学问题予以解决”.因此教师在教学过程中不能单纯或急于追求实现教学目标，而要根据具体的数学问题引导学生建立模型，还要不断地调整与创新，逐步培养学生解决数学问题的能力.

1 创设符合学情的学习环境，培养学生建模思想

数学教学的重要目的之一是培养学生的数学思维能力，因此课堂上必须创设良好的学习环境以促使学生学习.教师作为课堂教学的指导者，要根据学生的心理特点和实际情况来制定相应的学习方案，通过设计严谨的教学环节与有趣的数学问题，让学生进行数学思维的学习与训练，这是进行建模教学的前提与条件.

基于情境明确数学教学问题，逐步引导学生构建自身的数学思维体系.在数学教与学体系中，问题始终是核心，教师的教学需要将数学问题作为切入点.因此教师应善于利用教材，设计符合学生的学习情境，从而引导学生对建模思想产生兴趣.教师在这个过程中需要引导学生发现公式与定理的生成过程、原理与方法的获得过程、函数与方程模型的建立过程.

对互动合作的教学机制与模式进行创新，引导学生开展交流活动.在进行数学教学活动时，教师需要为学生们提供出更多的自我表达和互动交流的平台与机会，使学生能对自己的学习成果进行组织和梳理，并能清楚、准确地表达出来.

2 培养学生阅读理解能力，引导学生参与建模

苏联著名数学教育家斯托利亚尔曾经表示：在数学教学体系中，数学语言始终是知识的有效载体.那么，教师在进行实践教学工作时，我们需要关注学生自身数学阅读能力与素养的形成.课堂上抓住一切时机让学生进行阅读，自己理解，或与同学进行交流，切忌教师包办代替.还要教给学生科学合理的阅读方法，开始时教师可给予示范，接着让学生进行练习，带着学生进行不断地训练与强化，以达到培养学生主动阅读、有效阅读、科学阅读的良好习惯.

实际问题与方程、不等式、函数往往相结合，许多信息是“生活化”而非“数学化”的语言，数据多、关系隐蔽等等.因此，在平时的教学中教师要注重示范，教给学生提取关键信息的方法，教给学生如何抓住问题的本质，如何有效使用表格或画图的方法将问题形象化，建立起直观形象的数学信息.在面对较为复杂的问题时，指导学生理顺各种数量关系，并想方设法转化为数学的问题，呈现出问题中数学的“原貌”，为问题的解决铺平道路.

例如：在人教版的七年级上册教材当中有“电话计费”的问题，问题如下：下面表格各处的是两种不同类型针对移动电话的费用计算模式：

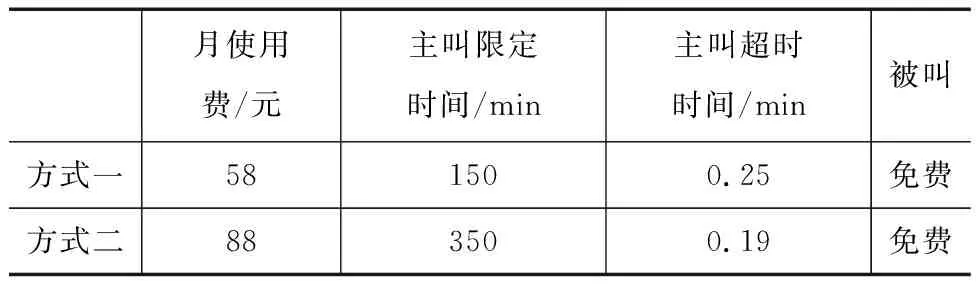
表1

你认为选择哪种计费方式更省钱呢？

A.对数学问题展开初步的解析与探索：假设一个月当中移动电话对应的主叫时间是t分(t代表的是正整数)．在对两种不同的模式进行比对时，先对如下表格进行设计：

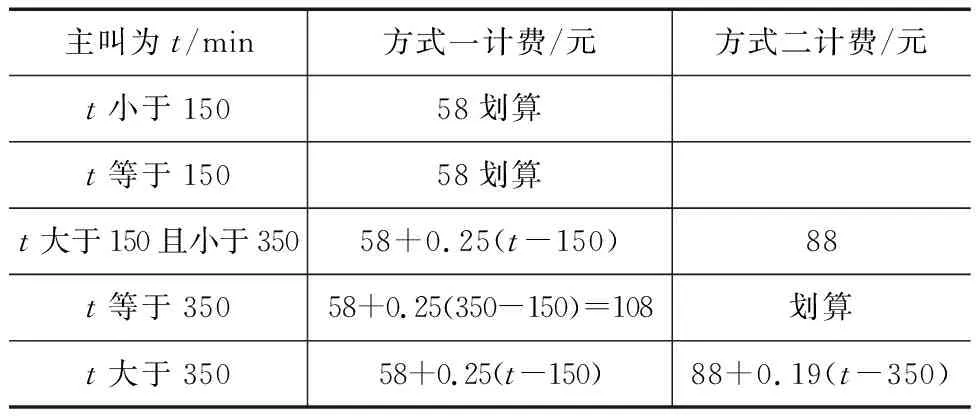
表2

B.对问题的深入探究：借助表格直观发现：当t大于150且小于350时，建立方程求出界点，即58+0.25(t-150)=88，解得t=270，故t小于270时，选择方式一省钱；t大于270时，选择方式二省钱．这类试题重点是“建立方程模型”，引领学生经历“猜想——探究——验证”的过程，也就是说教师不要急于呈现问题的结论，让学生体验建立方程模型解决实际问题的一般过程.

3 设计层次性的数学问题，引导学生主动建模

教学的过程是学生对新知识的认识过程，同时又是学生心智的发展过程，因此必须遵循循序渐进、由低到高、螺旋上升的原则.同时还要考虑数学问题的设置要符合学生的认知程度与解决问题的实际水平，特别是学生对实际问题的分析能力与读取信息的能力.

例如，进行围栏面积教学时，先设计出第一个数学问题：如下图1所示，用32 m长的围栏，一面靠墙(墙体可利用的最大长度为15m)，围成长方形的鸡舍．设与住房墙垂直一侧的鸡舍长度为xm，面积用Sm2来表示.当S=120 m2时，求所围长方形鸡舍的长、宽分别为多少？

图1 图2 图3

分析求长方形的面积首先要表示出长方形的长和宽，由鸡舍垂直于住房墙的一边为xm，利用总长32m的围栏减去垂直于住房墙的两边，就表示出平行墙的一边的长为(32-2x)m，学生很容易根据教师的引导列出一元二次方程：x(32-2x)=120，解得x1=6，x2=10．经检验当x1=6时，32-2x=20>15(不合题意，舍去)；当x2=10时，32-2x=12<15(符合题意)，故鸡舍的长、宽分别为12m、10m．

教师再次强调解决围栏问题首先是用未知数表示长和宽，然后建立方程模型，就能达到解决问题的目的.接着，追问：如果围成中间隔有一道栅栏的长方形鸡舍(如图2)，此时，如何表示长方形鸡舍的长和宽．学生根据刚才的解题经验很容易表示出鸡舍垂直于住房墙的一边为xm，平行墙的一边的长为(32-3x)m.

这时,我添加一个条件,当S=84 m2时，求鸡舍的长、宽各是多少米？

学生很快地建立方程模型：x(32-3x)=84，并解得x1=6，x2=14/3.经检验当x1=6时，32-3x=14<15(符合题意)；当x2=14/3时，32-3x=18>15(不符合题意，舍去)，故鸡舍的长、宽分别为14 m、6 m，问题就迎刃而解.

继续追问:为方便进出，在鸡舍的长和宽边上各留一个1 m的门(如图3)．此时，又如何表示长方形鸡舍的长和宽．

学生1：先垂直于住房墙的一边为xm，此时栅栏与留门分别xm与(x-1)m，用总长32m减去垂直于住房墙三边用的围栏，即[32-x-x-(x-1)]m，而{[32-x-x-(x-1)]+1}m就是表示平行墙的一边的长.

学生2：由前两个问题知在封闭的图形中，即不留门时很容易表示鸡舍的两边，故想象把留的门用材料堵上，留2个门就多准备这2个门的材料，所以问题就转化用34 m围栏围成图2的鸡舍分析即可.此时垂直于住房墙的一边为xm，平行墙的一边的长为(34-3x)m．

多好的想法呀，将“留门”问题变成“堵门”问题，很容易解决围栏“留门”的难题.

当S=96 m2时，求鸡舍的长、宽各是多少米？

学生都能快速地建立方程模型破解“留门”问题.如果课堂教学时间允许的话，还可以拓展鸡舍中间隔有2道栅栏或留更多的门的问题.

上述问题是由浅入深的进行，由围成1个长方形到2个长方形，在升级到“留门”，由封闭长方形到不封闭的长方形，从中归纳出不封闭化为封闭来破题，也让学生领略建立方程模型破解“留门问题”全过程,更能拓宽学生的视野,从而提升学生思维深度和缜密度.

4 巧用函数模型，破解最值问题

巧用函数模型解决数学问题，是初中学生学习的难点，也是中考的热点，如何把繁锁的问题进行转化是破题的关键.近些年来，在中考的函数应用类题目当中，融入了多元化的现实题材元素，结合实践生活背景创建数学题目，彰显出数学知识的实用价值，因为在高中数学体系内，函数占重要地位，函数思想方法的形成与否会对学生高中知识学习水平产生直接的影响.此外，在中考数学应用类题目当中，函数应用题出现得最多，是中考题的一大亮点，符合时代气息.因此，在课堂教学时，对“函数模型”的渗透是重中之重.

例如，某一公司的主营产品为某种类型的农产品，一箱此产品利用零售渠道获取的利润金额为70元，利用批发渠道获取的利润金额为40元．公司基于自身的经营性质作出规定，在产品总销售数量当中，零售产品数量不得超过30%．目前，此企业需要卖出1000箱此类农产品，应该怎样安排零售与批发的产品数量，企业才可以获取最大化的总利润？总利润最大为多少？

解设该公司利用零售渠道卖出m箱农产品，所获取的总利润数额为w元.那么，利用批发渠道卖出的农产品对应的数量则是(1000-m)箱，

因为该企业利用零售渠道卖出的产品数量不超过整体数量的30%，所以m≤300，结合题意信息可知，w=70m+40(1000-m)=30m+4000，m≤300．又因为30>0，所以w随着m的增大而增大，所以m=300时，取得最大值49000元，此时1000-m=700．

因此，此企业通过零售与批发渠道卖出的产品数量分别为300箱与700箱时，所获取的总利润是最多的，总利润最大值为49000元．

本题是一道对一次函数的实践运用的好题目：创建出一次函数的模型，运用一次函数自身的性质与自变量对应的取值范围来对最值的数学问题予以解决.

总之，数学问题中的许多背景素材，都与生活密切相关，在实践中发现数学问题，运用数学模型有效剖析问题，是在解决数学问题时所运用的一般性思路.其次，在解决几何问题时时常常用到方程与函数模型.在开展教学活动时，教师要认识到建模思想的重要性，设置合理的问题，引导学生深入探究，理解其内涵.