基于贝叶斯机械算法探究氯离子在钢筋混凝土结构中的扩散规律

喻宣瑞，刘慧平

（1.重庆交通大学土木工程学院，重庆 400074；2.中交三航重庆生态修复研究院，重庆 401120）

氯离子侵蚀钢筋混凝土基体从而诱发钢筋锈蚀，使得钢筋混凝土结构出现锈胀破坏，是影响钢筋混凝土结构耐久性的重要元凶.因此，揭示氯盐对钢筋混凝土构件的侵蚀机理，对于预测钢筋脱钝时间、延缓保护层开裂，提高结构在复杂服役环境中的耐久性与可靠性具有至关重要的意义［1-4］.

为此，有关学者开展了相应的试验研究，如孔德玉等［5］和Wang等［6-7］通过开展室内模型试验，模拟了氯离子对钢筋混凝土结构的侵蚀效应，得到了氯离子在混凝土各层间中的分布规律.陆春华等［8-13］发现氯离子在钢筋混凝土结构中的传输方式大致分为2种：稳态对流和非稳态扩散.对流一般发生在距混凝土面层2～3 mm内，氯离子浓度在该区域内会随着侵蚀深度的增加而升高；而扩散区域的氯离子浓度会逐渐降低.对流区氯离子的传递机制较为复杂，时常受到混凝土表面孔隙率和环境的共同影响，但相比扩散区而言，其影响范围较小，故在研究过程中一般忽略了对流区所带来的影响，主要研究氯离子在非稳态扩散区域中的传输规律［14］.Kranc等［15］基于Fick第二定律揭示了氯离子非稳态扩散的规律，提出了氯离子浓度预测模型.黄煜镔等［16］和张俊芝等［17］在Kranc等［15］的研究基础上还考虑了侵蚀时间对氯离子扩散的影响.但以上模型的精度都较为有限，与实测结果的系统误差值大多超过了15%，甚至某些模型误差达到了20%，这显然难以满足实际工程的需要.引起误差的原因大致可以归结于2点：一是在以往的模型中并未考虑钢筋对氯离子的阻碍效应，王元战等［18］研究发现钢筋对氯离子的传输有一定的阻滞作用，氯离子会在钢筋周围形成“堆积效应”；二是与模型中氯离子浓度的测试精度相关，表面氯离子浓度、氯离子传递系数等参数都是基于各层间氯离子浓度测量值进行回归计算所得，试验样本容量越大、测量数据越多，模型精度就越高.但是，在实际工程中所获取的试验样本和测量数据都较为有限，如何在有限样本的条件下提高预测模型的精度以满足实际工程要求就迫在眉睫.

鉴于此，本文通过模拟氯盐对钢筋混凝土的侵蚀作用，将氯离子非稳态扩散区划分为钢筋前沿区域和非前沿区域，以Fick第二定律为基础，对钢筋非前沿区域各层间的氯离子浓度进行预测，并提出相应的预测模型.在此基础上，考虑钢筋对氯盐的阻滞效应，引入钢筋阻滞系数对模型进行修正，得到钢筋前沿区域氯离子扩散预测模型，并通过贝叶斯理论，采用蒙特卡罗方法-马尔科夫链（MC-MC）进行系统抽样，修正了氯离子传输模型，提高了模型的计算精度，提出了氯离子在钢筋混凝土结构中的修正模型.

1 试验

1.1 原材料

P·O 42.5拉法基水泥；细度模数为2.5～3.0的中砂；粗骨料连续级配粒径位于5～20 mm之间［16］.减水剂采用高性能聚羧酸减水剂，减水率（质量分数）控制在20%左右.拌和水为蒸馏水，以最大限度保证混凝土内部氯离子浓度为0 mol/L.按表1所示的配合比来制作C35强度等级的混凝土试件［18］，水灰比（质量比）mW/mC=0.4.

表1 混凝土的配合比Table 1 Mix proportion of concrete kg/m3

1.2 试件制备及分组

根据表1中的配合比，分别制作7个尺寸为150 mm×150 mm×400 mm的试件，保护层厚度大约为20 mm，钢筋型号为HRB335热轧带肋钢筋，钢筋直径为16 mm，横向贯穿整个试件，如图1所示.将制作好的试件放置于（20±2）℃、相对湿度超过90%的恒温养护箱中养护24 h，待混凝土试件形成一定强度便拆除模具.随后，采用Ca（OH）2溶液对试件持续养护28 d，以防止混凝土在制作过程中掺杂氯盐.养护完成后，将试件表面进行切割抛光，采用环氧树脂对其余5个面进行密封，剩余1个端面暴露在环境当中，作为氯盐侵蚀面.待环氧树脂凝结后，将其放置于配有3.5%（质量分数，下同）NaCl溶液 的 环 境 箱 内［16］，如 图2所 示.每 隔7 d更 换1次NaCl溶液，以最大限度保证腐蚀环境中的氯离子浓度保持不变.

图1 钢筋混凝土试件Fig.1 Reinforcement concrete specimens

图2 环境箱Fig.2 Environment device

当试验分别进行到35、65、100、140、175、200、235 d这7个时间（t）时，将试件取出并测定其中各层的氯离子浓度（C）.具体过程如下：取出试件对其表面进行清洗，从氯离子侵蚀表面逐渐沿着氯盐的侵蚀路径进行研磨并逐层取样（见图3），在研磨初期和靠近钢筋附近区域按1 mm间隔进行研磨，中间区域（大约在4～15 mm之间）按2 mm间隔进行研磨［7］.研磨完成后，将其溶于加有AgNO3的溶液中，经过蒸发结晶来测量各层间不同时段的氯离子浓度.

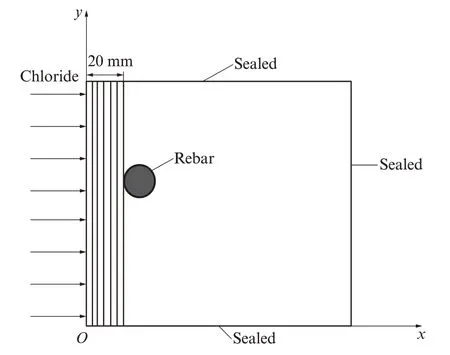
图3 氯离子浓度测定的取样方法Fig.3 Method of taking sample for determination of chloride ion concentration

2 结果与分析

氯离子浓度随扩散深度（x）的变化如图4所示.由图4可见：

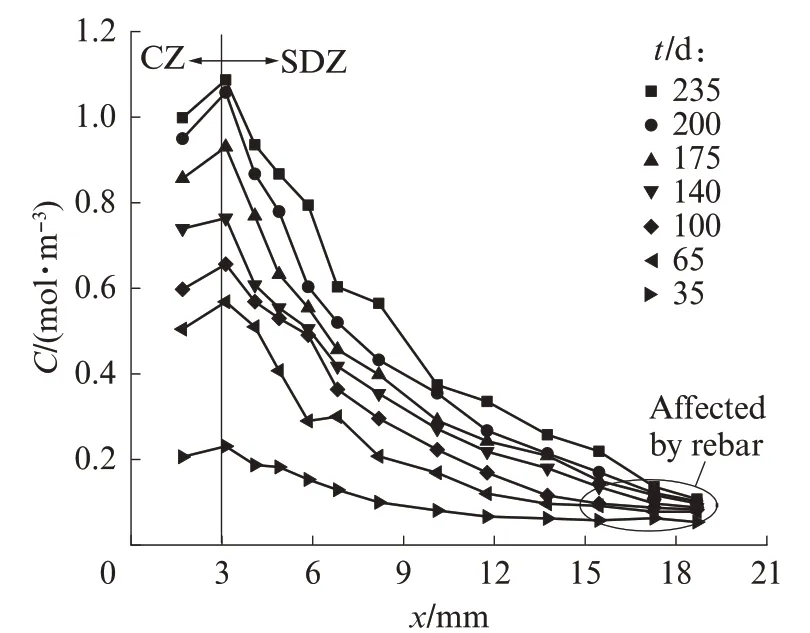
图4 氯离子浓度随扩散深度的变化Fig.4 Variation of chloride concentration with diffusion depth

（1）在混凝土层间（0～3 mm）内氯盐浓度呈现上升趋势.这说明在距离试件表层3 mm内形成了对流区（CZ），致使氯离子浓度在局部范围内随扩散深度的增加而升高，所得试验结果与相关文献较为吻合［9-13］.

（2）当扩散深度大于3 mm时，此时处于稳态扩散区（SDZ），氯离子在各层间的浓度呈现下降趋势，尤其是在3～15 mm之间其下降趋势十分明显，当扩散深度增加到15～20 mm时，氯离子浓度的下降趋势减缓，随时间的变化趋势也不再显著.这与吴林键［19］的研究较为一致.当钢筋嵌入混凝土结构中时，钢筋对氯离子传输将起到一定的阻滞作用，使得氯离子在钢筋的前沿区域堆积.

从试验结果可看出，氯离子进入钢筋混凝土构件中主要通过对流和非稳态扩散2种方式，相比对流区域，非稳态扩散区占据了主导地位.故大多数的研究主要还是针对氯离子的非稳态扩散区（3～20 mm）.对于氯离子在非稳态区的扩散规律可采用Fick第二定律来描述，氯离子在钢筋混凝土结构中本应是一个三维扩散的过程，但由于其复杂的扩散机制，目前绝大多数的研究主要还是仅从一维的角度来考虑氯离子的传递机理［17-18］.若仅考虑氯离子在混凝土中的一维扩散模型，则氯离子浓度与氯离子扩散系数（D）的关系如式（1）所示.

若将氯离子在混凝土中的扩散系数考虑为一常数时，结合初始边界条件C（x＞3 mm，t=0）=C0，C0为混凝土内部初始氯离子浓度；C（x＞3 mm，t＞0）=Cs，Cs为表面氯离子浓度，可以得到氯离子在混凝土各层间浓度的表达式：

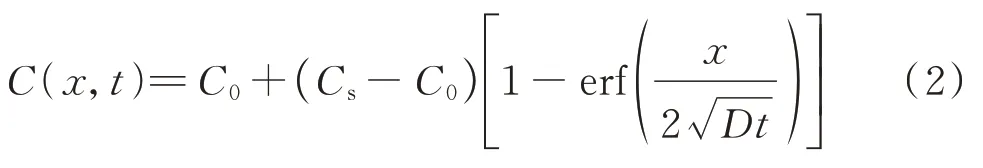
式中：erf(x)为误差函数，具体表达方式如式（3）所示，可通过最小二乘法进行回归求解.

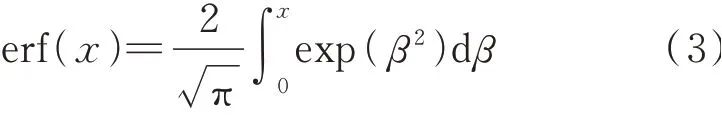
假定混凝土内部的初始氯离子浓度为0 mol/L，式（2）可进一步简化为：

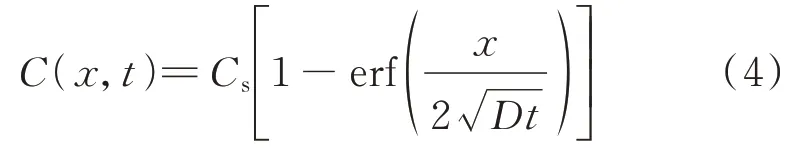
考虑到实际环境中混凝土表面氯离子浓度等参数的时变规律［18］，可将式（4）进一步改写为：

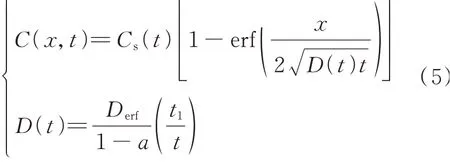
式中：Derf为参考氯离子扩散系数；a为龄期系数；t1为参考扩散时间，一般取28 d［18］；D(t)反映了氯离子扩散系数的时变规律；Cs(t)为表面氯离子浓度的时变函数，mol/m3.

基于最小二乘法原理，采用式（6）中C(x，t)的表达式对图4中实测各层间的氯离子浓度进行拟合，可回归得到D(t)和Cs(t)的时变规律，如图5所示.

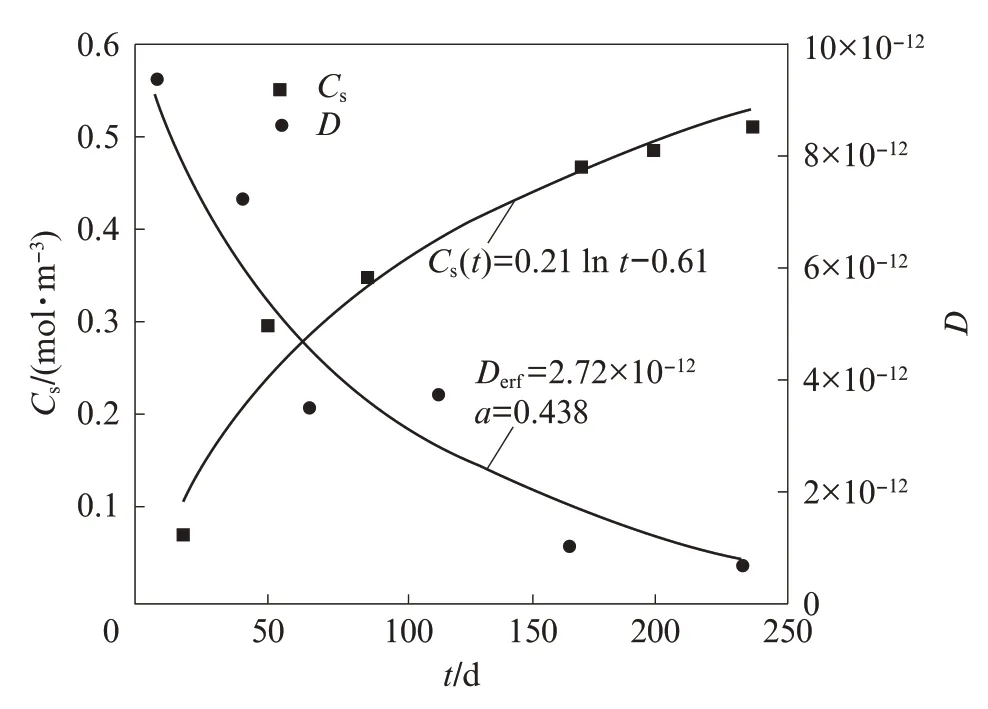
图5 氯离子浓度、氯离子扩散系数的时变规律Fig.5 Time varying law of chloride concentration and chloride diffusion coefficient

吴林键［19］研究发现，采用对数函数来模拟混凝土表面氯离子的时变规律最佳.通过对图5中的离散点进行回归，得到Cs(t)=Alnt+B.同理，采用式（5）中D(t)的表达式对图5中的离散点进行回归分析，可以得到Derf=2.72×10-12和龄期系数a=0.438.将以上参数代入式（5）中，可以建立氯离子扩散的预测模型1（Model 1），如式（6）所示（模型1主要针对非稳态扩散区3～20 mm）.

3 基于贝叶斯理论修正氯离子扩散模型

传统的统计学精度主要取决于数据样本的质量和数量，当数据样本较为有限时，预测模型计算结果与实际观测结果就会产生较大误差.在实际工程中，获取的实测样本数据较为有限，如何通过有限的样本数据来建立具有较高精度的预测模型就显得十分重要.随着机械算法和大数据理论的诞生，这一问题得到了很好的解决.近年来，在科学和工程的各个领域，机器学习方法在解决工程检测和模型性能预测方面得到了极大的关注.贝叶斯统计模型定义量化了模型表示数据的程度，通过有限的样本容量，利用MC-MC抽样进行数据更新，最终确定了模型本身可靠性的概率.

贝叶斯理论考虑了参数的随机性，假设其服从某一先验概率分布，通过MC-MC抽样进行数据更新逼近，得到后验概率分布，将二者进行比对，以此来验证模型的正确性，具体表示方法如下［20］：

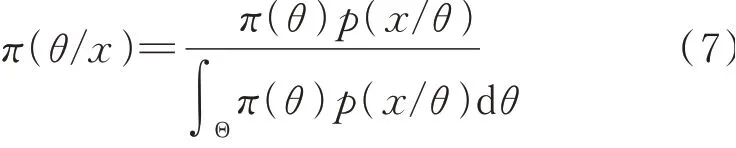
式中：θ表示所修正的参数，通常情况下可假设其服从正态分布；π(θ)表示该参数的先验分布概率；p(x/θ)表示抽样分布形式；π(θ/x)为后验分布概率.当后验分布概率与先验分布概率不断逐次逼近（位于置信区间内）时，则更新完成.为了让修正结果具有较高精度，预估计失效概率设定为0.005，抽样次数满足如下要求［21］：

式中：pf表示预估计失效概率；N表示随机抽样次数，随机抽样次数设定为2万次.

得到钢筋混凝土构件表面氯离子浓度表达式中参数A、B的概率分布直方图，并通过曲线进行拟合，得到参数A的均值为0.197 2，方差为0，067；B的均值和方差分别为-0.620 4和0.072.同理，参考氯离子扩散系数Dref的均值和方差分别为2.715×10-12和0.016，龄期系数a的均值和方差分别为0.518和0.057.并采用卡方检验对以上分布模型进行相关验证，得到以上4个参数的变异系数分别为0.023、0.037、0.042、0.045，4个系数都小于0.05且位于置信区间内.

将各参数的修正结果代入式（6）中，得到修正后的氯离子扩散预测模型，如式（9）所示，将其命名为模型2（Model 2）.

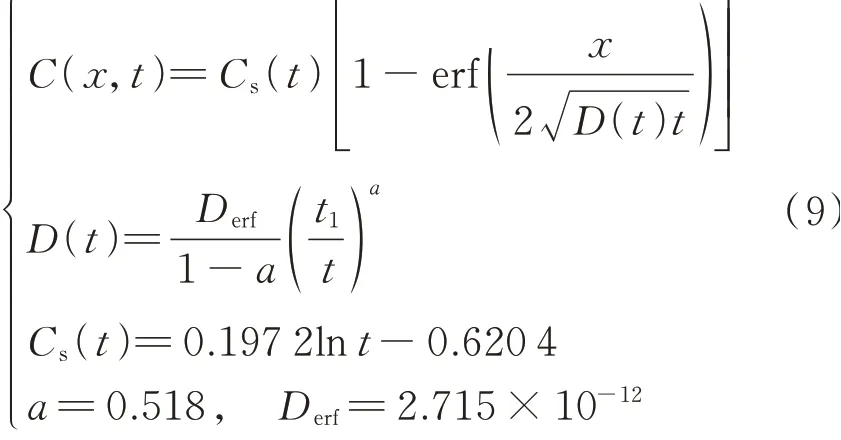
4 模型验证对比分析

为了验证模型1和模型2的精度，通过模型1和模型2分别计算得到混凝土各层间的氯离子浓度，将其与实测值进行比较，部分对比结果如图6所示.

由图6可知，与修正前的模型相比，修正后模型的精度得到了较大程度的提高，但是在钢筋前沿阻滞区域内（15～20 mm），无论是修正后的预测模型还是修正前的预测模型，其预测结果都远低于实测值，这可能是由于钢筋对氯离子传输的阻滞效应所致.为直观展示2个模型的预测精度，其相对误差如图7所示.

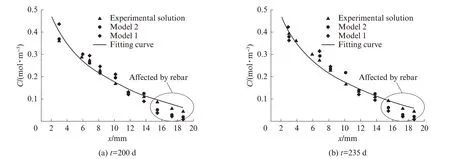
图6 氯离子浓度的对比Fig.6 Comparison results of chloride concentration

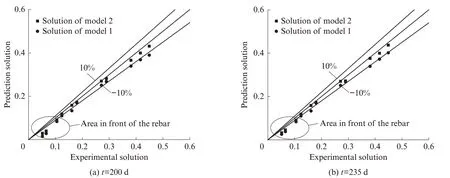
图7 相对误差值Fig.7 Relative error value

由图7可见：未修正的预测模型（Model 1）所计算得到混凝土各层间氯离子浓度与实测结果作比对，其误差值大多在10%以外；经过修正后的模型（Model 2）其精度得到了相应的提高，在钢筋非前沿区域（3～15 mm），其误差值位于10%以内，但对于钢筋前沿区域，预测结果与实际结果偏差较大，故模型2仅能预测钢筋非前沿区域（3～15 mm）各层间氯离子的浓度，对钢筋前沿区域（15～20 mm），钢筋对氯离子扩散的阻滞效应十分显著，氯离子浓度会显著提高，因此需对这一区域的氯离子浓度分布规律进一步研究.

5 钢筋对氯盐扩散的阻滞效应

钢筋嵌入混凝土结构中会对氯离子的扩散起到一定的阻滞效应，尤其是在钢筋前沿区域表现得十分明显.使得氯离子在钢筋附近堆积，最终导致钢筋前沿区域氯离子浓度增大.为了描述钢筋对其前沿区氯离子扩散的影响，提出钢筋阻滞系数（ID）来量化钢筋的阻滞效应，定义如下：

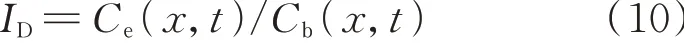
式中：Ce(x，t)表示当扩散时间为t时，在钢筋前沿区域内（15～20 mm）氯离子浓度实测值；Cb(x，t)为模型2的计算结果.

分别将t=65、140、175 d情况下的Ce(x，t)和Cb(x，t)值代入式（10）中，可计算得到钢筋的阻滞系数，其结果如图8所示.

图8 钢筋的阻滞系数Fig.8 Blocking effect coefficient of rebar

从图8可以看出，ID在不同时段的计算结果与其平均值之间的相对误差仅在4%以内，故取ID的平均值1.621为钢筋的阻滞系数.将ID=1.621引入模型2，从而建立考虑钢筋阻滞效应的氯离子扩散预测模型，但该模型主要是针对钢筋前沿区域氯离子扩散的模拟（x=15～20 mm），将该模型命名为模型3（Model 3），如式（11）所示.

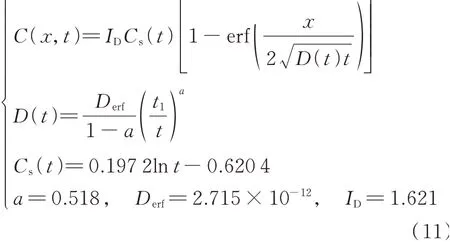
通过模型3计算得到钢筋前沿区域各层间氯离子浓度，将其与模型2和实测数据对比，对比结果如图9所示.由图9可知，修正后的预测模型计算所得到钢筋前沿区域各层间的氯离子浓度相比模型2的计算精度明显提高，经过误差分析，通过模型3所计算得到的结果与实测结果相比，相对误差位于10%以内.说明模型3能够较好地预测钢筋前沿区域各层间氯离子浓度的分布规律.

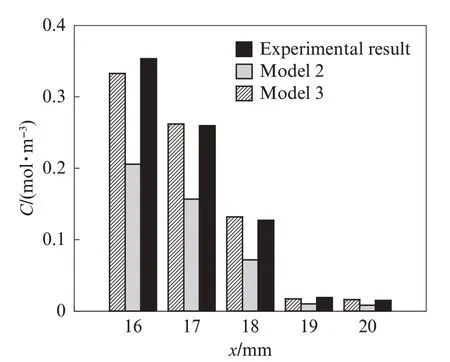
图9 氯离子浓度计算对比分析结果Fig.9 Comparison results among Model 2，Model 3 and the experimental data

6 结论

（1）钢筋会影响其前沿5 mm处的氯离子扩散，使得氯离子在其前沿堆叠，致使氯盐浓度提高.

（2）针对钢筋非前沿扩散区域，基于Fick定律提出了氯离子浓度预测模型.考虑到样本的局限性和测量数据的质量与精度，通过贝叶斯理论模型进行修正，得到修正过后的氯离子扩散预测模型，其精度得到显著提高.

（3）通过定义钢筋的阻滞系数来量化钢筋前沿区域（15～20 mm）对氯盐扩散的阻滞效应，其阻滞系数为1.621.