A modified forward and backward reaching inverse kinematics based incremental control for space manipulators

Gangqi DONG ,Panfeng HUANG,* ,Yongjie WANG ,Rongsheng LI

a National Key Laboratory of Aerospace Flight Dynamics,Northwestern Polytechnical University,Xi’an 710072,China

b Research Center for Intelligent Robotics,School of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China

KEYWORDS Forward and backward reaching inverse kinematics(FABRIK);Incremental control;Inverse kinematics;Manipulator control;Robotic capture

Abstract Forward and backward reaching inverse kinematics (FABRIK) is an efficient two-stage iterative solver for inverse kinematics of spherical-joint manipulator without the calculation of Jacobian matrix.Based on FABRIK,this paper presents an incremental control scheme for a free-floating space manipulator consists of revolute joints and rigid links with the consideration of joint constraints and dynamic coupling effect.Due to the characteristics of FABRIK,it can induce large angular movements on specific joints.Apart from that,FABRIK maps three dimensional (3D) problem into two dimensional (2D) problem by a simple geometric projection.This operation can cause infinite loops in some cases.In order to overcome these issues and apply FABRIK on space manipulators,an increments allocation method is developed to constrain the angular movements as well as to re-orient the end-effector.The manipulator is re-positioned based on the momentum conservation law.Instead of pure target position tracking,the orientation control of the end-effector is also considered.Numerical simulation is performed to testify and demonstrate the effectiveness and reliability of the proposed incremental control approach.

1.Introduction

Due to the growing application demands for automation,dexterity and efficiency in On Orbit Servicing (OOS) and Active Debris Removal (ADR) missions,robotic capture by space manipulator has been considered as one of the most promising techniques.1–3Generally,a space manipulator is mounted on certain ‘‘floating base”,such as satellite,spacecraft,space station,etc.According to the momentum conversation law,the motion of the manipulator varies the position and orientation of the floating base,and the translation and rotation of the base in turn affects the motion of the manipulator as well.This kind of phenomenon is called dynamic coupling.4

The effect of dynamic coupling can be neglected in cases where the mass and inertia of the space manipulator are much smaller than the base,or the position and orientation of the base are fully controlled.In such cases,the space manipulators are usually approximated as fixed base manipulators,similar to those on the ground.5,6During the past several decades,plenty of work has been reported in the literature dealing with the target estimation,motion planning and control issues of fixed base manipulators,which can be easily transplanted to tackle similar problems of space manipulators when the fixed-base approximation holds.It is worth mentioning that the fixed-base approximation may degrade the control accuracy and the dynamic performance.

The control of space manipulators will be complicated when dynamic coupling is not negligible.Generally,the control objective of a manipulator is a desired position of the end-effector in the Cartesian space,and the control input is the angular position or the angular velocity in joint space.7,8Existing control schemes can be classified into three categories:dynamics-based,data-based and kinematics-based.

Remarkable amount of the control approaches in the literature are dynamics-based.Nevertheless,in dynamics-based approaches,many parameters need to be measured and fed back in practice,such as angular position and velocity,force/-torque etc.Besides,model uncertainties and external disturbances are usually troublesome to cope.9With the consideration of dynamic coupling,Vafa and Dubowsky10introduced an analytical modeling method for space manipulators called the virtual manipulator (VM),which could be considered as an ideal kinematic chain with a fixed virtual base.Liang et al.11proposed an practical solution to map a floating base manipulator to a fixed base manipulator,named dynamically equivalent manipulator (DEM),with preserving both dynamic and kinematic properties.Both VM and DEM involve a passive spherical joint,which is not controllable.Based on the momentum conservation law,Umetani and Yoshida12derived a new Jacobian matrix for space manipulators called the generalized Jacobian matrix (GJM),which enabled the extension of a variety of control methods developed for a fixed base manipulator to a space manipulator by simply replacing the traditional Jacobian matrix into GJM.Due to the development of artificial intelligence technology,data-based approaches have emerged in recent years.The advantage of data-based approaches is that they do not require the dynamic and/or kinematic model of the manipulator,which is generally favored,especially when the model is hard to derive or highly nonlinear.But data-based approaches require large a priori data set to ensure the training accuracy of the model,which may not available in space applications.

Intuitively,it is more convenient to control a space manipulator by joint angles,like in those kinematics-based approaches.13,14However,the inverse kinematics will be encountered.By adopting pseudo-inverse of the Jacobian matrix and considering angular velocity limits as constraints,a predictive kinematic control scheme and an incremental kinematic control scheme were reported respectively,where the Jacobian matrix should be non-singular.15,16Yang et al.17transformed the motion control of a dual-arm space manipulator to an optimization problem as well.With joint acceleration considered as the control input,the end-effector could achieve the predefined waypoints without consideration of inverse kinematics.Xu et al.18proposed a hybrid modeling and analysis method to deal with the dynamic coupling.By resolving the linear and angular momentum conservation equations in different ways,the calculation of Jacobian matrix and its inverse was avoided.Aristidou and Lasenby19developed an efficient iterative solver for inverse kinematics in frame animation production,called forward and backward reaching inverse kinematics (FABRIK),where the Jacobian matrix was avoided.The FABRIK can easily incorporate with joint constraints,and is appropriate for multiple chains with multiple end-effectors.However,it tends to induce large angular movements on specific joints due to the characteristics of FABRIK,which is subject to the configuration of manipulator as well as the desired position and orientation of the end-effector.Furthermore,the FABRIK maps 3D problem into 2D problem by a simple geometric projection,this may cause infinite loops in specific cases.

In order to overcome the abovementioned issues and adaptively applying the FABRIK to address the control problem of a space manipulator,an angular increments allocation method is developed in this paper to break the infinite loops as well as to re-allocate the angular movements.Moreover,instead of pure target position tracking in the FABRIK,the orientation control of the end-effector is also considered.

The remainder of this paper is organized as follows.In Section 2,the basic procedures of the FABRIK in two dimensional case and three dimensional case are formulated,and the problems of applying FABRIK on space robotic manipulators are pointed out.A modified FABRIK-based incremental control approach is described in Section 3.In order to validate the proposed approach,numerical simulation results are reported and analyzed in Section 4.The conclusion of the paper is summarized in Section 5.

2.Preliminary

The FABRIK is an iterative solution for inverse kinematics.As the name implies,the basic procedure of one complete FABRIK iteration can be divided into two stages:the forward(inward) reaching stage and the backward (outward) reaching stage.19A schematic diagram of the FABRIK for a two dimensional(2D)chain with fixed base connected by 1 DOF(degree of freedom) revolute joints is shown in Fig.1,where Fig.1(a)to Fig.1(c) describe the forward reaching stage,and Fig.1(d)to Fig.1(f) describe the backward reaching stage.

Fig.1 A schematic diagram of one complete iteration of FABRIK in 2D.

Therefore,the steps of the forward reaching stage can be concisely formulated as

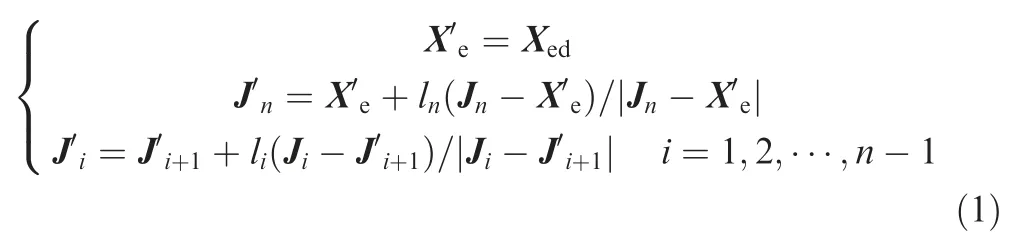
The backward reaching stage re-evaluates each of the joint position starting from the root joint to the end-effector.In order to distinguish from forward reaching stage,the position of each joint as well as the end-effector are with a two-prime superscript.The procedure of the backward reaching stage is described by the following steps:

Consequently,the steps of the backward reaching stage can be formulated as

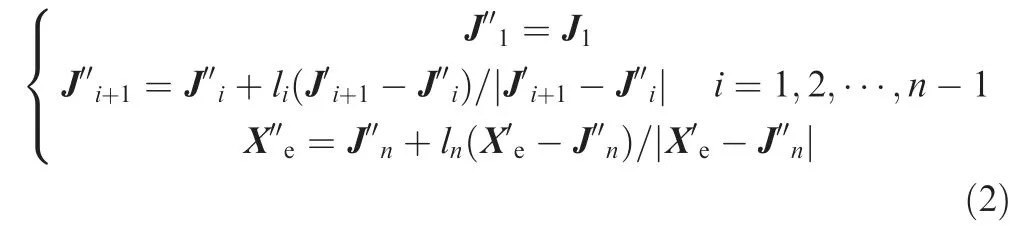
After one iteration of steps (a) to (f),the procedure is repeated until the desired position of the end-effector is achieved.From the above procedure,it is noted that the FABRIK is prone to induce large angular movements on specific joints,such as those close to the end-effector in Fig.1.

For three dimensional (3D) cases,the procedure described above can be directly adopted if a chain is connected by ideal ball-and-socket joints (3 DOFs).Considering the fact that robotic manipulators are connected mostly by revolute joints to achieve 3D motion of the end-effector in practical applications,the forward reaching stage is remaining the same as Eq.(1),and the re-evaluation procedure of a revolute joint position with joint restriction in the backward reaching stage is depicted in Fig.2(a).Becauseshould be within the dash line plane,in order to determinethe position ofis replaced by its projection onto this plane,denoted by

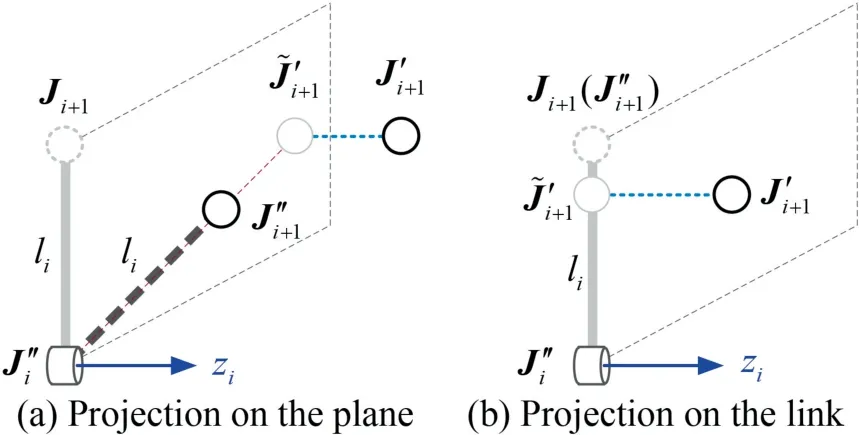
Fig.2 Geometric projection in backward reaching stage.

The DH frames of a multi-joint robotic manipulator are defined accordingly,20and let Tidenote the homogenous transformation matrix from the inertia frame to theith DH frame.The elements of Tiare trigonometric functions of joint variablesq1,q2,···,qiand other DH parameters.Then according to the DH convention,Ticould be easily obtained.Further define the projection matrix as

3.FABRIK-based incremental control

In order to adopt FABRIK to solve the position tracking control problem of a space manipulator,the forward reaching stage is remaining the same as described in Section 2.Considering the fact that the robotic manipulator is assumed as spherical-joint (3 DOFs) type in the forward reaching stage,and the end-effector is oriented to the desired position with the consideration of robotic geometry only.Subsequently,the angular movements as well as the robotic configuration may be impossible to be achieved by the revolute-joint (1 DOF)space robot.Therefore,in the backward reaching stage,the end-effector is re-oriented by applying physical constraints to limit the joint velocity,and considering the rotational degree of freedom of the revolute-joint to update the robotic configuration.

In the backward reaching stage,the position of the base do not need to keep because of the free floating nature.Therefore,the position of the root joint is set to maintain the estimated position in the forward reaching stage.In order to distinguish notations from Eq.(5),it is written as

In order to constrain the angular movements,joint velocity limits are applied while re-evaluating the next joint position.First,according to the geometric projection method illustrated in Fig.2,find the position of the（i+1）th joint,denoted assuch that

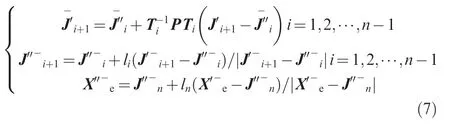
Define the dimensionality reduction matrix as

Such that the movements of each joint position with respect to the revolution plane of the previous joint can be determined by

Ifxi,thex-axis of theith DH frame,is parallel with linkliand pointing to Ji+1,as shown in Fig.3(a),the incremental joint angle is calculated by

Ifyi,the y-axis of theith DH frame,is parallel with linkliand pointing to Ji+1,as shown in Fig.3(b),the incremental joint angle should be calculated by

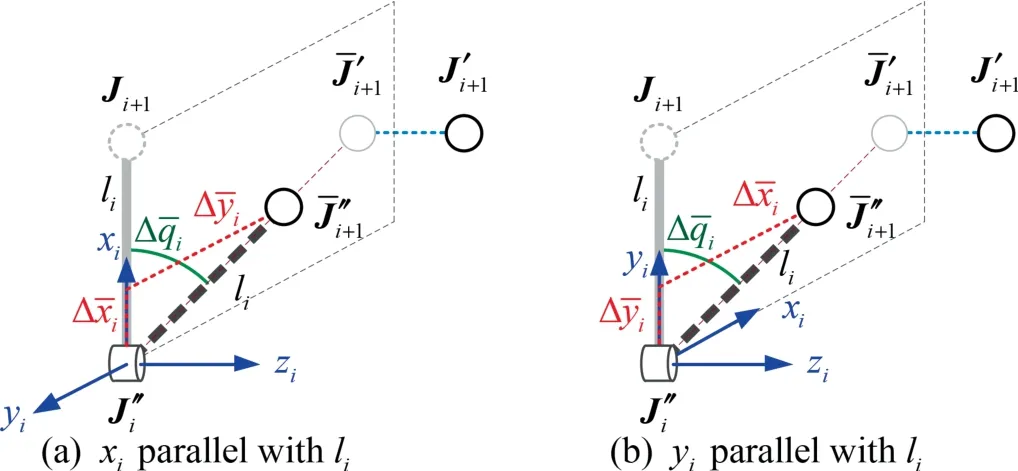
Fig.3 Projection in backward reaching stage with consideration of joint restriction.

Ifzi,the z-axis of theith DH frame,is parallel with linkliand pointing to Ji+1,the joint angle is set the same as the previous one,that is

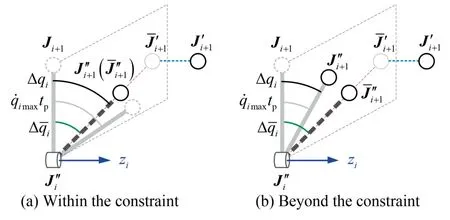
Fig.4 Process of constraining angular movement.

Subsequently,the Cartesian coordinates of the joint with respect to the inertia frame are determined by

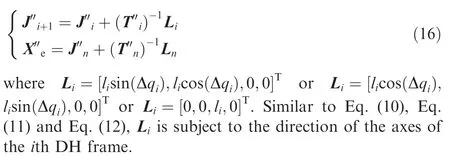
The process described by Eqs.(6)–(16) indicate the modified backward reaching stage with the consideration of joint constraints.Consequently,the end-effector is reoriented,meanwhile,the joint velocity limits are applied to constrain the angular movements.

For a free floating space manipulator,as illustrated in Fig.5,the center of mass can be calculated by

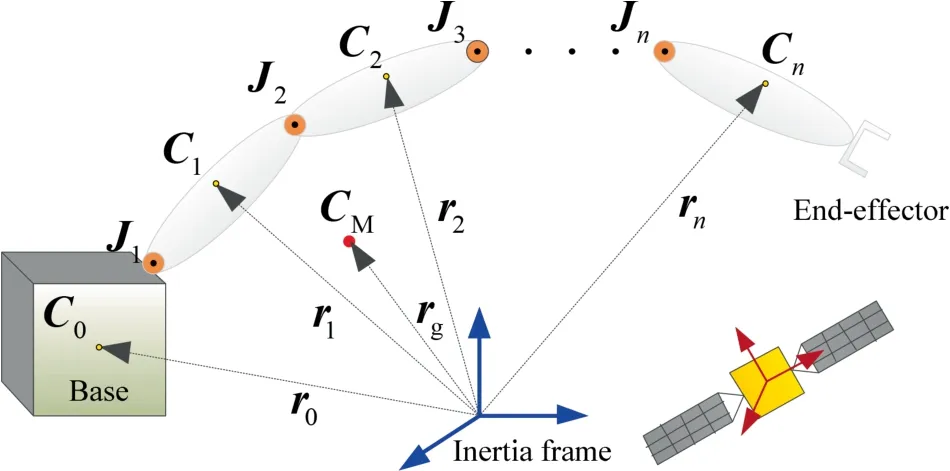
Fig.5 An illustration of a free floating space manipulator.

wheremiis the mass of each link (or base),riis the vector pointing from the origin of the inertia frame to the center of mass of each link(or base)Ci,and rgdenotes the vector pointing from the origin of the inertia frame to the center of mass of the space manipulator.To keep dimensional consistence,riand rgare also extended to homogeneous formation.

After the new backward reaching stage,the center of mass of the space manipulator is

To perform robotic capture,not only the desired position should be achieved,but also the end-effector should approach the desired position in specific direction as shown in Fig.6(a).If misalignments exist,as shown in Fig.6(b),capture failure will most likely occur,and may cause serious consequences.

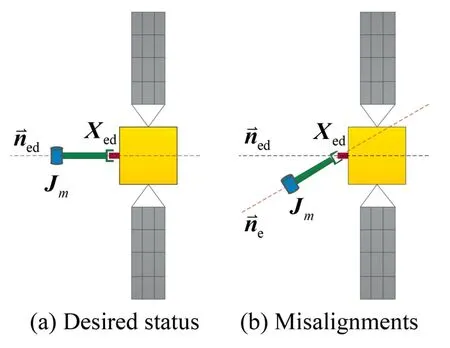
Fig.6 Robotic capture scenarios.

Without loss of generality,the desired orientation of the end-effector is denoted asSince the end-effector is fixed to the last link,the nearest joint should achieve a desired position in order to satisfy both position and orientation requirements of the end-effector.It is worth mentioning that the revolute axis of the joint,denoted by Jm,should not be parallel with the last link.The desired position of this joint is

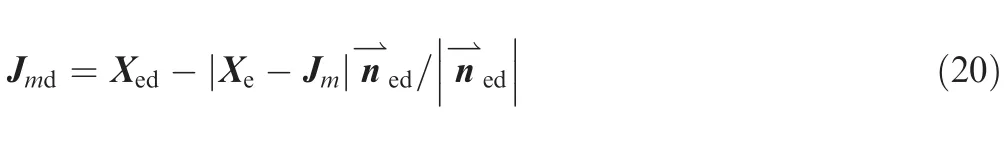
It is noted that the desired position of the joint is derived by both the desired position and orientation of the end-effector.Therefore,once the desired position of the last joint is achieved,both the desired position and orientation of the end-effector could be achieved.To conclude the modified FABRIK-based incremental control,the pseudo code of the iterative control procedure is presented as

4.Simulation results and analysis

In order to validate the proposed incremental control scheme,numerical simulation is performed on a 6R free floating robotic manipulator.The initial position of the manipulator and possible assignment of DH frames are shown in Fig.7.The inertia frameOxyzis fixed in the space.

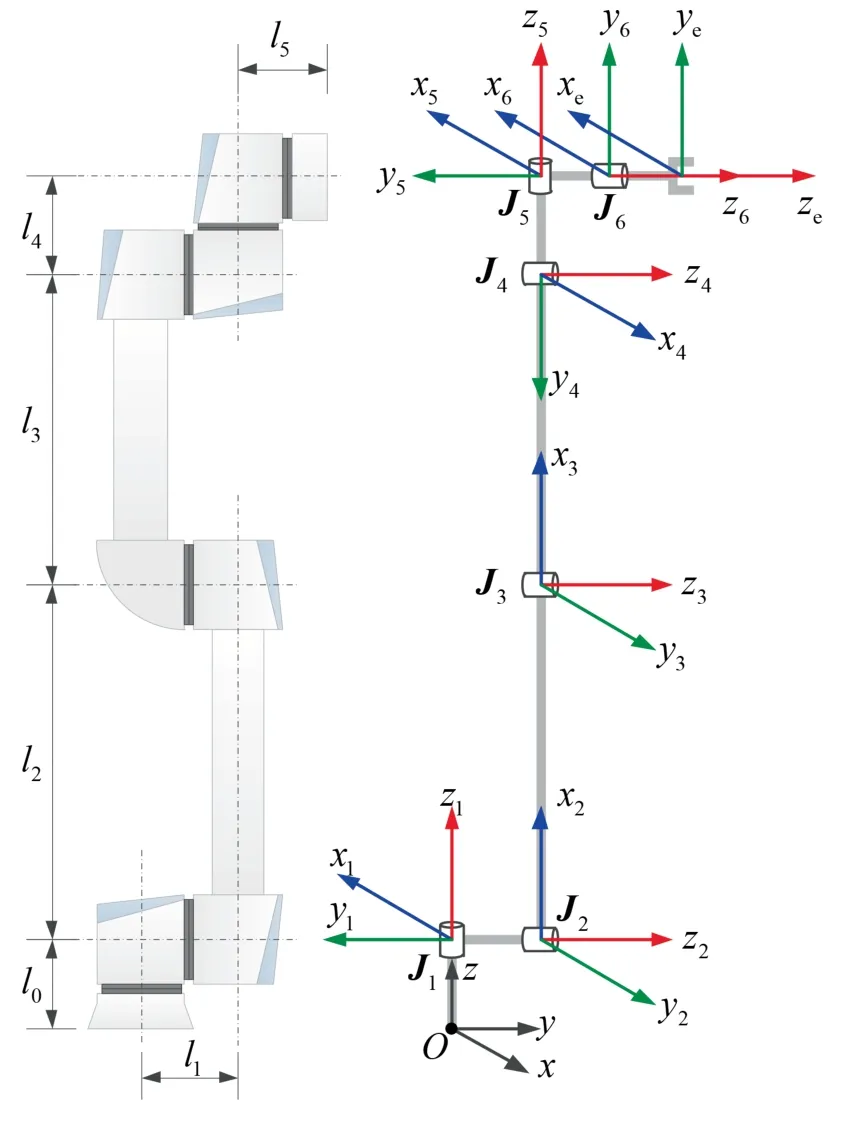
Fig.7 Initial position of manipulator and assignment of DH frames.

The prototype of the manipulator is UR5 (universalrobots),and the joint velocity limits are ±180（o）/s for all the joints.In the simulation,the manipulator is assumed to be mounted on a 100 kg free floating base satellite,the link length and mass are listed in Table 1.Accordingly,the DH parameters are listed in Table 2,whereq1,q2,···q6denote the joint variable.

Table 1 Length and mass distributions.

Table 2 DH parameters of space manipulator.

Within the working space,for given desired position and orientation of the end-effector in homogenous formation,such as Xed=[0.3 m,0.5 m,0.8 m,1]Tand=[1,1,-1,0]T,set the control period astp=0.01 s and tolerance as 0.01 m,the simulation results are shown in Figs.8–10.

Fig.8 intuitively shows the configuration of the manipulator at typical time steps.Starting from the home position,the end-effector moves towards the desired position as expected.Simultaneously,joint 5 approaches its desired position in order to achieve both the desired position and orientation of the endeffector.

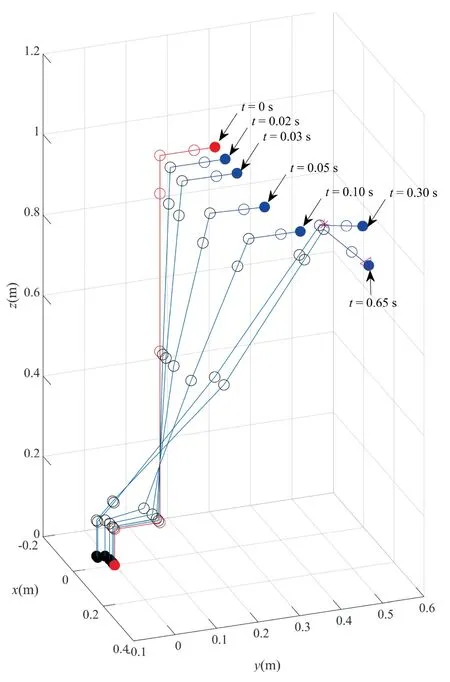
Fig.8 Configuration of manipulator at typical time steps.

Fig.9 shows the trajectory of the end-effector.It can be seen that the end-effector achieves the desired position after 0.62 s.Because thez-axis of joint 6 is parallel with link 5 and link 6,as shown in Fig.7,it has no contribution to the position of the end-effector.The corresponding joint angles are shown in Fig.10.The large variation of joint angles are mainly caused by the setting of joint velocity limits.Moreover,as formulated in Eq.(20),the desired position and direction of the end-effector are mapped to the desired position of the last revolute joint,where the revolute axis is not parallel with the last link.Then because the revolute axis of joint 6 is parallel with link 5 and link 6,the desired position and direction of the end-effector in the simulation are mapped to the desired position of joint 5.According to the proposed approach,the desired position and direction of the end-effector could be achieved by the first five joints.As a result,joint 6 becomes independent,which could be utilized for adjusting the angular bias between the endeffector and the grasping feature on the target.The above simulation results indicate that the proposed approach is effective in position and orientation control.

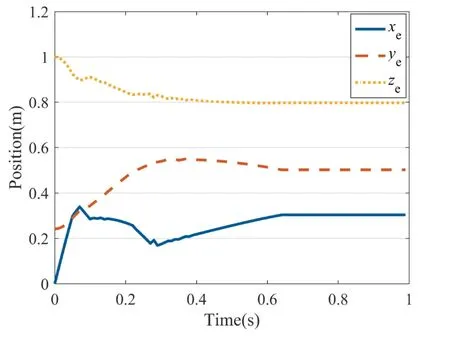
Fig.9 Trajectory of end-effector.

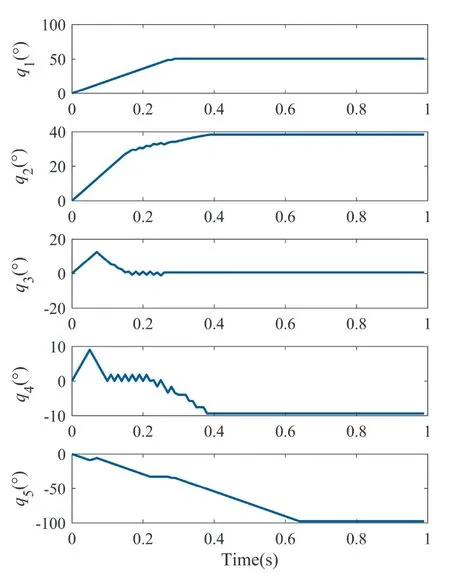
Fig.10 History of joint angles.

5.Conclusion

This paper presents an incremental control scheme for a freefloating space manipulator based on modified FABRIK.FABRIK is an efficient iterative solver for inverse kinematics of spherical-joint robotic manipulators.But in practical applications,most of the manipulators are consisted of one degree of freedom revolute-joint.In order to achieve both the desired position and orientation of the end-effector,the desired position of the nearest joint to the end-effector is derived,where the revolute axis of the joint is not parallel with the last link.Then the joint position is set as the derived desired one in the procedure of forward reaching stage.During the backward reaching stage,incremental joint angles are obtained ultimately with the consideration of joint velocity limits as well as the dynamic coupling effect.The advantages of the proposed scheme could be summarized as: (a) the basic FABRIK is modified for solving the inverse kinematics of practical revolute-joint robot;(b)because the end-effector is re-oriented in the modified backward reaching stage,the infinite iteration problem of the basic FABRIK is eliminated;(c) it is a Jacobian-free approach,such that,the complex calculation of matrices and non-singularity assumption of the Jacobian matrix is avoided;(d) Since the control input is incremental joint angle,multiple-solution-problem of robotic inverse kinematics is avoided.Numerical simulation results demonstrate the effectiveness of the proposed control scheme.The calculation of Jacobian matrix and the multiple solution issues are avoided by the proposed approach,which is generally favored in robotic capture and has great potential in practical applications.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This study was supported by the National Natural Science Foundation of China(Nos.61803312,91848205 and 61725303).