基于坐标变换的功能梯度材料空间映射建模研究

韩晓伟，段国林，王世杰，韩 硕，马 硕，杨 杰

（河北工业大学机械工程学院，天津 300401）

功能梯度材料（functionally graded material,FGM）是一种可实现某些特殊功能的新型非均质材料[1]，其从内部组分、结构到物理特性和化学特性等方面均呈现连续的变化。与传统单一材质材料相比，功能梯度材料具备很多特殊的优点：既可解决非均质材料的界面应力问题，又能保持材料的复合特性[2]。功能梯度材料最早应用于航空、机械领域中需耐高温、腐蚀和磨损的结构[3]，现已扩展到核、生物、热电或热离子转换、医学和电磁等领域[4]。在功能梯度材料的制备过程中，最重要的是采取合适的措施来确保材料在组成、结构上的梯度变化，其制备过程通常结合材料复合技术、计算机辅助材料设计和制造技术[5]。功能梯度材料可通过利用物理或化学方法将金属、高分子聚合物以及陶瓷等结合的方式来制备。传统的制备方法有物理化学气相沉积法、粉末冶金法、等离子喷涂法和自蔓延高温合成法等[6]。功能梯度材料在各类对材料有特殊要求的领域中有广阔的应用前景[7]。

功能梯度材料建模是其制备过程中的关键环节。但是，传统的三维CAD（computer aided design，计算机辅助设计）建模方法对实体模型的表示主要基于构造表示和边界表示[8]，且将模型内部视作单一均质材料来处理，只能表示实体外表面的基本信息，而难以表示其内部的材料结构和组织信息。因此，需要设计可实现模型几何信息与材料信息有效结合的方法，以满足功能梯度材料建模的要求。

为此，吴晓军等[9]提出了基于八叉树的体素化建模方法，即采用几何运算方法体素化三维网格模型，该方法可建立材料分布不均匀的模型，但只能通过体素根据一定的分辨率逼近实体，导致模型的精度较低，且储存体素需要大量空间。Biswas等[10]提出了一种基于距离场的建模方法，通过精确或近似于材料特征的距离对空间进行参数化，该方法适用于大多数尺寸、形状和拓扑结构等材料特征，缺点是计算过程繁琐。Jackson等[11]提出将几何信息与材料信息赋予有限元网格节点的建模方法，但基于有限元网格建立的模型由于被细分成小四面体单元，使得后续的切片等数据处理复杂化。张贺等[12]提出了利用等值面表示材料信息的建模方法，通过对不同层的等值面进行处理，可以实现不同几何形状和不同材料分布的功能梯度材料的建模，但该方法只限于材料分布呈等值面均匀分布的情况。葛正浩等[13]提出了基于控制点的建模方法，该方法假设几何空间由空间点组成，利用梯度源方法将材料信息附着于空间点，以实现材料信息的映射，该方法适用于构建简单模型或回转体模型，但建模过程繁琐，对材料分布复杂的零件处理困难，且大量的点会占用较多的储存空间。Yang等[14]提出了一种基于B样条的建模方法，通过异质材料放样构建异质体模型，该方法不需要设置控制点网格，而是直接通过配置模型材料特征来设计材料分布和几何形状。

综上所述，功能梯度材料建模需要建立几何空间和材料空间并将其有效结合。其中，几何空间可通过建模软件直接构建，材料空间的构建可通过功能梯度材料结构设计来完成[15]。传统的功能梯度材料建模方法通常先将几何模型离散成体素或四面体，而后将材料信息导入离散的体素或四面体[16]。离散重组的方法虽然简化了建模过程，但通过一定分辨率逼近实体的方法会大大降低模型的精度，且随着分辨率的增大，所需储存空间增大，导致后续处理变得复杂。为方便几何信息与材料信息的结合，笔者提出一种新的基于坐标变换的功能梯度材料空间映射建模方法，通过基于坐标变换的映射方法来避免传统功能梯度材料建模精度低的弊端。

1 功能梯度材料建模设计

功能梯度材料建模时，首先要定义模型几何空间，然后设计模型材料分布以得到所需的梯度变化，从而确定材料空间和映射关系，最后基于映射关系将材料模型从材料空间映射到几何空间，以构建功能梯度材料模型。通过空间映射建模的核心是确定材料空间到几何空间的映射关系，即定义功能梯度材料的材料组分变化规律，这个变化规律用关于几何空间坐标的函数表示。当存在多个映射关系时，映射关系具有严格的作用区间，即在从材料空间向几何空间映射的过程中，不同区间对应不同的映射函数。

定义欧几里得空间为E3，功能梯度材料建模空间B=G3×M，其中G3表示三维几何空间，G3⊆E3，M表示材料空间，n表示功能梯度材料所含材料的种类（n≥1），则功能梯度材料模型可表示为：

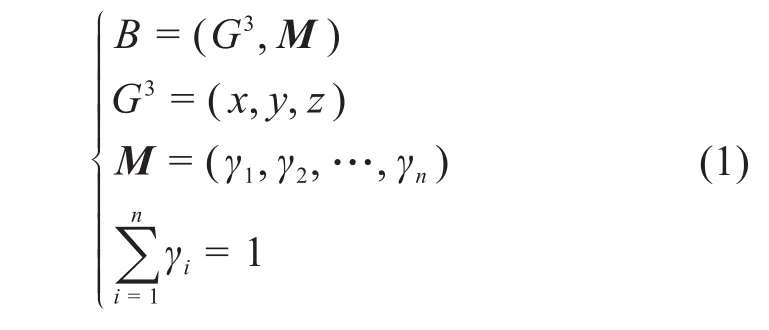
式中：(x,y,z)为几何空间坐标；γi为某点处第i种材料（i=1,2,…,n） 的占比，0≤γi≤1，γi=0表示该点不含第i种材料，γi=1表示该点只含第i种材料。

将材料空间中的材料分布情况按照映射关系映射到几何空间中，得到各材料相在几何空间中的空间分布情况，而后将各材料相的分布组合起来，即可得到功能梯度材料模型。以包含3种材料（m1、m2、m3）的功能梯度材料模型为例，其几何空间到材料空间的映射关系如图1所示。

图1 某功能梯度材料模型几何空间与材料空间的映射关系Fig.1 Mapping relationship between geometric space and material space of a functionally graded material model

根据材料变化的复杂程度，将基于空间映射的功能梯度材料建模大致分为3种情况。

1）材料组分以单一函数规律变化的功能梯度材料模型。

材料组分以单一函数规律变化的功能梯度材料模型大多属于几何形状简单的模型。如图2所示，某一预打印条块由2种材料（m1、m2）组成，其中材料m1、m2的体积分数分别用函数f1、f2表示，则图2所示的材料m1的梯度变化规律分别为：f1(x)=x，f1(y)=y，f1(x)=x2-x+1，f1(x,y)=0.25xy+0.5x-0.5y。相对应的，材料m2的梯度变化规律f2=1-f1。函数f1与f2即构成该预打印条块的材料分布函数F。对于材料组分以单一函数规律变化的功能梯度材料模型，材料空间到几何空间的映射只有一个映射规律，在这种情况下，材料分布函数与映射关系一致。

图2 材料组分以单一函数规律变化的功能梯度材料模型Fig.2 Functionally graded material model of material composition changing with single function law

2）材料组分以多个函数规律变化的功能梯度材料模型。

如图3所示，对于材料变化规律比单一函数复杂的功能梯度材料模型，其往往需要多个映射关系来确定。

图3 材料组分以多个函数规律变化的功能梯度材料模型Fig.3 Functional gradient material model of material composition changing with multiple function laws

对于图3所示情况，一般认为材料是多个方向变化的且每个方向满足一定的映射关系。在不同的材料变化区域，分别确定相应的映射关系Φ1,Φ2,…,Φj,…,Φq，如式(2)所示：

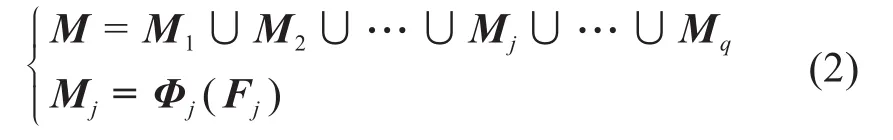
式中：Mj为材料空间的某一区域；Fj为区域Mj的材料分布函数；Φj为材料空间到几何空间的映射关系。

当材料组分以多个函数规律变化时，功能梯度材料建模要解决多个梯度源下材料接触区域材料过渡时的平滑性以及连续性。在这种情况下，多个映射关系对应多个梯度变化规律。以多个函数规律变化的功能梯度材料模型的映射关系如图4所示。

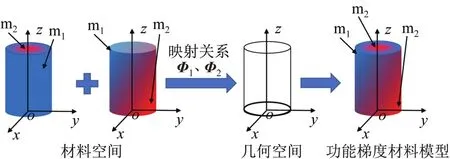
图4 材料组分以多个函数规律变化的功能梯度材料模型的映射示意Fig.4 Mapping schematic of functionally graded material model of material composition changing with multiple function laws

3）无映射规律的功能梯度材料模型。

在实际应用中，往往存在材料变化规律较为复杂的功能梯度材料模型，这些模型一般不存在映射规律。对于无映射规律的功能梯度材料模型，通常采用点云法、体素法或切片处理法进行建模。其中，体素法是将几何模型离散成体素点，并将材料信息添加至每一个体素点来完成建模的，将材料信息加到每一个体素点即可认为是一种映射。基于体素法的功能梯度材料模型的空间映射如图5所示。

图5 基于体素法的功能梯度材料建模映射示意Fig.5 Mapping schematic of functional gradient material modeling

通过以上分析，除第3种情况外，均可根据实际需要设计功能梯度材料从材料空间到几何空间的映射关系，而第3种情况虽然没有具体的映射规律，但可以根据转换算法得到材料梯度信息，即第3种情况也可以认为具有多个映射关系。因此，可以统一用材料分布函数来表达功能梯度材料中的材料组分体积占比信息，即功能梯度材料模型的每一个映射关系对应一个材料分布函数。

2 功能梯度材料建模表示

2.1 基于梯度源法的材料空间建立

本文采用梯度源法来表示功能梯度材料的材料分布，以建立材料空间。选取功能梯度材料模型中的一些特征作为参考特征（即梯度源），以模型上任意一点到梯度源的欧氏距离作为自变量来设计材料分布函数。为方便材料分布函数的计算，通常选取特殊的特征作为梯度源。

2.1.1 单梯度源法

如图6所示，对于仅含单个梯度源的功能梯度材料模型，通常选取圆心、球心、轴心线或底面等作为梯度源，较为复杂的也可选取表面轮廓作为梯度源。

图6 点、线、面单梯度源功能梯度材料模型Fig.6 Functionally graded material model based on single point,line and plane gradient source

对于单梯度源功能梯度材料模型，其材料分布函数F(x,y,z)是一个由一组材料组分梯度变化规律函数构成的向量：

式中：fi(x,y,z)表示第i种材料组分在(x,y,z)处的分布规律，各个材料在空间某一点处的体积分数之和等于 1，即。

材料分布函数可以为线性或非线性，根据不同材料分布函数建立不同维度的材料空间。图7所示为由2种材料构成的一维、二维、三维材料空间，其材料分布函数分别表示为：

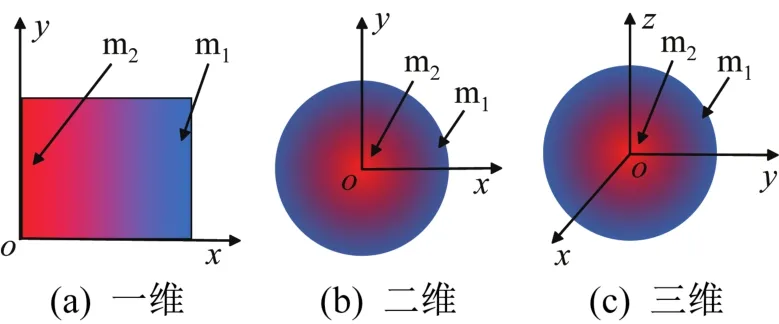
图7 不同维度的材料空间示意Fig.7 Material space of different dimensions

式中：L为正方形边长；r为圆形半径；R为球体半径。

选取不同的梯度源可以得到不同的梯度变化规律，通过修改几何形状、梯度源和材料分布函数，可得到所需的功能梯度材料模型。

2.1.2 多梯度源法

在实际的功能梯度材料建模设计中，材料变化往往不是单一材料的简单变化，而是多种材料的复杂变化，则会出现多个梯度源。多个梯度源的情况可分为2种：非交叉梯度源和交叉梯度源。

1）非交叉梯度源。

当同一模型中出现2个或多个梯度源时，功能梯度分级区域之间会发生交集。图8所示为具有2个梯度源（G1和G2）的功能梯度材料模型，其从材料m1变为材料m2和从材料m2变为材料m3的2个梯度变化区域之间不相交，将这种不同梯度变化区域共存而互不干扰的梯度源称为非交叉梯度源。

图8 非交叉梯度源功能梯度材料模型Fig.8 Functionally graded material model of non-cross gradient source

对于2个非交叉梯度源的梯度变化区域，分别根据空间点与梯度源G1、G2之间的欧式距离d1、d2来定义梯度变化区域的材料组成。若空间点更接近梯度源G1（即d1＜d2），则根据梯度源G1计算材料组成，反之亦然；若空间点与2个梯度源的距离相等（d1=d2），则根据任意梯度源计算材料组成。对于含多个非交叉梯度源的功能梯度材料模型，可以此类推。

2）交叉梯度源。

若图8所示的2个梯度变化区域相交时，该相交区域的材料组成利用相交算子“⊗”根据用户定义的权重比进行求和。

式中：k1、k2分别为不同梯度源的权重比；F1、F2分别为不同梯度源的材料分布函数。

式(4)表明，通过控制梯度源的权重比即可实现对不同交叉梯度源的控制。对于具有更为复杂材料分布的功能梯度材料模型，其可能含有2个以上的交叉梯度源。当存在多个交叉梯度源时，相交区域的材料组成可用式(5)计算：

式中：m为梯度源个数。

与单梯度源功能梯度材料模型一样，多梯度源功能梯度材料模型中各个材料在空间某一点处的体积分数之和也等于1，即：

式中：Fti为第t个梯度源中第i种材料的材料分布函数。

2.2 材料空间到几何空间的映射

根据已建立的材料空间，确定从材料空间映射到几何空间的映射函数。在大部分情况下，几何空间与材料空间的坐标系不重合，导致空间映射无法进行。因此，实现2个空间坐标系的重合为实现几何信息和材料信息有效结合的关键，即需要找到一个映射矩阵以实现材料空间到几何空间的映射。利用坐标变换法，即通过平移、旋转、缩放、投影等一系列坐标变换可实现材料空间与几何空间的坐标系重合。本文以平移变换和旋转变换为例，说明材料空间到几何空间的映射流程。平移变换和旋转变换可分别表示为：

式中：tx、ty、tz为3个方向的平移距离；θ为旋转角度。

图9所示为基于坐标平移变换的材料空间到几何空间的映射流程（以球形材料空间映射到正方体几何空间为例）。

图9 基于坐标平移变换的材料空间到几何空间的映射流程Fig.9 Mapping process from material space to geometric space based on coordinate translation transformation

图9所示材料空间中的材料分布函数可表示为：

鉴于只需平移即可将材料空间映射到几何空间，根据F′(x,y,z)=ΦF(x,y,z)，可得映射后的材料分布函数F′(x,y,z)：

由此可得，最终功能梯度材料模型的材料分布函数为：

图10所示为基于坐标旋转变换的材料空间到几何空间的映射流程（以横向圆柱形材料空间映射到纵向圆柱形几何空间为例）。

图10 基于坐标旋转变换的材料空间到几何空间的映射流程Fig.10 Mapping process from material space to geometric space based on coordinate rotation transformation

图10所示材料空间中的材料分布函数可表示为：

式中：H为圆柱的高度。

鉴于图10所示是将材料空间沿x轴旋转θ=90°后映射到几何空间，则可得：

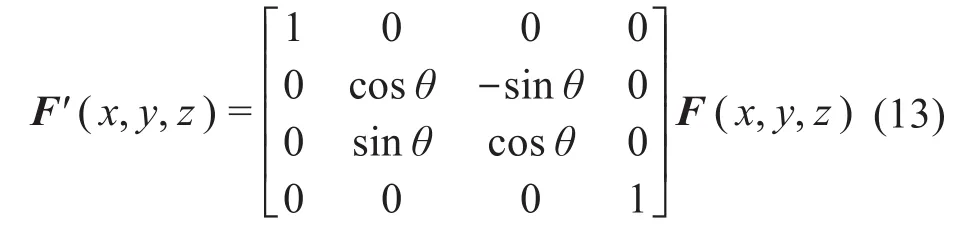
由此可得，最终功能梯度材料模型的材料分布函数为：

其中：

式中：r1为圆柱的底面半径。

3 实例建模及OpenGL可视化分析

根据上述基于坐标变换的功能梯度材料空间映射建模方法，在Visual Studio 2019软件与OpenGL编程语言下，分别对单梯度源和多梯度源功能梯度材料进行建模。

3.1 基于单梯度源的实例建模

基于图9所示的坐标变换方法，对尺寸为100 mm×100 mm×100 mm的正方体功能梯度材料模型进行实例建模。利用式(7)和式(9)计算得到加入材料信息后功能梯度材料模型的材料分布函数。同时，通过OpenGL可视化分析显示最终的功能梯度材料模型，如图11所示。在OpenGL程序中，用R（红）、G（绿）、B（蓝）表示不同的材料。

图11 单梯度源正方体功能梯度材料模型的可视化结果Fig.11 Visualization results of cube functionally graded material model with single gradient source

3.2 基于多梯度源的实例建模

锥齿轮可以传递2个不平行轴之间的运动和动力，具有传动效率高、传动比准确和使用寿命长等优点，在实际生产中被广泛应用。但在一些特殊场合下，锥齿轮各个位置的磨损有所不同，则要求其不同位置处材料的硬度应有所区别，为典型的多梯度源。下文将针对未加工齿的功能梯度材料锥齿轮毛坯件进行建模分析。

假设锥齿轮毛坯件内部有2种材料变化规律，如图12所示，其中一种是从轴线到外表面的径向梯度变化，另一种是从底面到顶面的轴向梯度变化，可分别建立2个梯度源G1和G2。

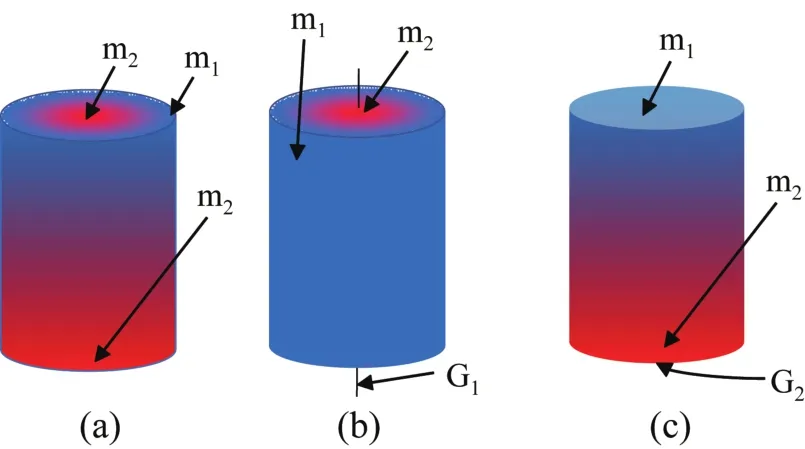
图12 锥齿轮毛坯件的材料空间分解示意Fig.12 Material space decomposition of bevel gear blank

图12(b)所示的梯度源G1的分配数据如下：

1）材料梯度变化方式为沿圆柱中心轴向外扩散；

2）参考特征为圆柱中心轴；

4）权重比k1=0.5。

图12(c)所示的梯度源G2的分配数据如下：

1）材料梯度变化方式为沿圆柱底面向上扩散；

2）参考特征为圆柱底面；

4）权重比k2=0.5。

鉴于梯度源G1和梯度源G2为交叉梯度源，根据权重比k1和k2，利用相交算子“⊗”对2种不同的梯度源进行求和，最终得到的材料分布函数为：

由此得到的功能梯度材料模型具有如图12(a)所示的2个方向的材料分级。对于未加工齿的功能梯度材料锥齿轮毛坯件（大端圆的直径为100 mm），其材料空间到几何空间的映射流程如图13所示。

图13 锥齿轮毛坯件材料空间到几何空间的映射流程Fig.13 Mapping process from material space to geometric space of bevel gear blank

由图13可知，要使两坐标系重合，需要进行的坐标变换如下：1）绕x轴顺时针旋转90°；2）沿x轴平移50 mm；3）沿z轴平移50 mm。由此可得，最终锥齿轮毛坯件的材料分布函数为：

代入具体参数的数值并简化，可得：

由此可得，映射关系为：

通过OpenGL可视化分析可得多梯度源功能梯度材料锥齿轮毛坯件的模型，如图14所示。

图14 多梯度源功能梯度材料锥齿轮毛坯件模型的可视化结果Fig.14 Visualization results of functionally gradient material bevel gear blank model with multiple gradient sources

上述建模实例的结果表明，本文所提出的建模方法有助于避免某些不同材料组成连接处材料的急剧变化，因此可以抑制材料界面区域的严重应力集中和热失配。

在利用基于坐标变换的功能梯度材料空间映射建模方法处理交叉梯度源模型时，可根据人为设定的权重比，较容易地实现对材料空间中材料信息的修改，且利用坐标变换进行映射可大大缩短建模时间。表1所示为本文坐标变换算法与估值建模中普通体素化算法以及非估值建模中显式函数算法的建模时间对比。

表1 坐标变换算法与其他算法的建模时间对比Table 1 Comparison of modeling time between coordinate transformation algorithm and other algorithms单位：s

4 结论

针对功能梯度材料建模研究，提出了一种基于坐标变换的功能梯度材料空间映射建模方法，即通过坐标变换将几何空间与材料空间有效结合起来，进而建立所需的功能梯度材料模型。该方法较其他方法有如下优点。

1）基于坐标变换的功能梯度材料空间映射建模方法通过坐标变换有效地结合了几何信息与材料信息，可通过映射函数将材料分布映射至几何模型，建立所需的功能梯度材料模型。同时，通过OpenGL可视化分析，利用RGB颜色显现，可以清晰表示所建立的模型。

2）通过建模实例与建模时间比较可知，基于坐标变换的功能梯度材料空间映射建模方法大大缩短了建模时间，从根本上解决了一些算法造成的储存空间不足和建模过程繁琐等问题，使得功能梯度材料模型的设计变得直观且具有灵活性。

然而，本文提出的基于坐标变换的功能梯度材料空间映射建模方法还有一定的局限性。当建立具有复杂几何形状或者具有多种材料分布的功能梯度材料模型时，表示几何信息或者材料信息的解析函数也会变得非常复杂，使得某些部分的计算变得困难，而且通过非估值建模方法建立的模型在进行材料查询时并不方便。今后有必要开展材料分布函数简化研究，以简化具有多个材料分布的模型材料空间的坐标变换过程，并优化相应程序，使得材料查询更加方便。