基于电流解耦的表贴式永磁同步电机无源控制研究

樊峰宇，周兆忠，赵 颖，汪 骏

（衢州学院机械工程学院，浙江衢州 324000）

永磁同步电机具有良好的动、静态性能和较低的能量损耗，被广泛应用于工业机器人、数控机床和新能源汽车等[1]。作为一个多变量、强耦合的非线性系统[2]，永磁同步电机的电流环常采用PI（proportional integral，比例积分）控制算法。但随着工业发展水平的不断提高，对永磁同步电机控制性能的要求越来越高，使得传统的PI控制已不能满足系统的高精度控制要求。因此，多种非线性控制算法开始得到应用，如反步控制、滑模控制和无源控制等。其中，无源控制是从系统能量角度出发，将永磁同步电机看作一个电能为输入、机械能为输出的能量转换装置[3]，利用能量平衡原理，基于端口受控耗散哈密顿系统（port control Hamilton system with dissipation,PCHD），通过互联和阻尼配置的无源控制（interconnection and damping assignment passivity-based control,IDA-PBC）方法进行无源控制器设计。

针对无源控制方法，国内外学者进行了大量的研究。吕成兴等[4]为提高电力双推进无人船的能量利用率，采用无源控制方法对无人船用永磁同步电机的速度控制进行研究，并通过仿真验证了该方法可有效降低驱动系统的能量损耗和提高无人船的续航能力。付晓阳等[5]针对永磁同步风力发电系统在低风速下的最大功率追踪，提出了一种无源控制与扩张状态观测器相结合的控制策略，仿真结果表明该方法具有较强的转速控制性能和抗负载扰动能力。Mocanu等[6]将无源控制与干扰观测器相结合，通过观测器对电气和机械扰动进行观测与补偿，提高了永磁同步电机的控制性能和稳定性。何洁等[7]结合无源控制与鲁棒控制技术，设计了鲁棒无源控制器，提高了永磁同步电机无源控制的稳定性，并设计了基于负载转矩观测的速度环滑模观测器，增强了永磁同步电机驱动系统的负载适应性。任丽娜等[8]提出了一种基于无源控制与增广无迹卡尔曼滤波模型的无速度传感器控制策略，有效地减小了由电阻摄动引起的转速误差，提高了永磁同步电机驱动系统的鲁棒性。程启明等[9]提出了一种基于准Z源矩阵变换器的永磁同步电机无源控制系统，该系统具有较好的动、静态性能和抗干扰能力，有效提高了永磁同步电机驱动装置的电压传输比及其调速范围。Liu等[10]针对由永磁同步电机驱动的关节式机器人，设计了一种基于位置误差的平滑切换函数，实现了永磁同步电机控制方式在单环反馈线性化控制与无源控制间的平滑切换，从而使机器人系统具有良好的动态和稳态性能。李红斌等[11]为提高永磁同步电机的控制性能，将负载扰动观测器与无源控制器相结合，经仿真验证该控制算法具有良好的控制性能与抗扰动能力。刘佳雯等[12]提出了一种控制策略平滑切换方案，使永磁同步电机驱动系统根据需要在反步积分滑模控制和无源控制间进行切换，提高了该系统的抗干扰能力和控制精度。侯利民等[13]基于表贴式永磁同步电机的PCHD模型设计了整形控制器，并结合滑模控制有效抑制了负载扰动，改善了其驱动系统的动态品质。金宁治等[14]结合自抗扰技术与无源控制技术，设计了一种新的内置式永磁同步电机控制系统，提高了系统的响应速度与抗干扰能力。袁宏哲[15]为提高永磁同步电机的动态性能，结合线性自抗扰控制技术与无源控制技术，对其位置控制进行了研究，仿真结果表明，所设计的控制算法具有良好的控制性能和较强的抗干扰能力。Belkhier等[16]将非线性观测器与IDA-PBC方法相结合，设计了一种新型控制算法并将其应用于永磁同步电机，同时通过仿真验证了该控制算法的有效性。

然而，在基于PCHD的表贴式永磁同步电机无源控制器的设计过程中，因d轴与q轴电流存在耦合，使得期望互联矩阵的未知参数过多，增加了设计的复杂性，且已有研究缺乏对采用无源控制器时电流环响应带宽的测试。为减少期望互联矩阵中的未知参数，笔者提出了一种基于电流解耦的无源控制器新型设计方法，并通过实验测试电流环的响应带宽和转速响应性能，以验证所提出方法的有效性。

1 基于PCHD的IDA-PBC方法

1.1 PCHD的数学模型

基于欧拉-拉格朗日方程获得PCHD的数学模型[17]：

式中：x为状态变量；u为控制器；H(x)为系统能量函数；J(x)为互联矩阵，表征系统内部的互联结构，J(x)=-JT(x)；R(x)为阻尼矩阵，表征系统的端口阻性结构，R(x)=RT(x)；ξ为外部干扰；g(x)为外部互联矩阵。

1.2 IDA-PBC方法

针对基于PCHD的无源控制器的设计问题，Ortega[18]提出了IDA-PBC方法。该方法通过配置互联矩阵、阻尼矩阵和能量函数来设计无源控制器，使得给定的PCHD在该控制器的作用下转换为一个期望的PCHD，该期望PCHD在期望平衡点处稳定运行。期望PCHD的数学模型可表示为：

式中：Jd(x)为期望互联矩阵，表征期望系统内部的互联结构；Rd(x)为期望阻尼矩阵，表征期望系统的端口阻性结构；Hd(x)为期望系统的能量函数，其在系统稳定运行的平衡点处有严格的极小值。

一般的非线性系统可表示为：

式中：f(x)、h(x)为关于状态变量x的任意函数。

根据文献[19]中的定理2-1，对于式(3)所示的非线性系统，当存在反对称互联矩阵Jd(x)和半正定对称阻尼矩阵Rd(x)，使得式(4)所示的偏微分方程有解时，其无源控制器u的求解方法如式(5)所示。

式中：g⊥(x)g(x)=0。

2 表贴式永磁同步电机的无源控制器设计

2.1 表贴式永磁同步电机的数学模型

表贴式永磁同步电机是一个多输入、多输出、高阶、强耦合的非线性系统，其在d-q坐标系下的数学模型可表示为：

式中：I为转动惯量；Ld、Lq分别为电机在d-q坐标系下的d轴和q轴电感；id、iq分别为电机在d-q坐标系下的d轴和q轴电流；ud、uq分别为电机在d-q坐标系下的d轴和q轴电压；Rs为定子电阻；TL为负载转矩；Ψf为永磁体产生的磁链；P为电机的极对数；ωm为电机的机械角速度。

2.2 基于电流解耦的无源控制器新型设计方法

由式(6)可知，表贴式永磁同步电机的d轴、q轴电流相互耦合，其耦合关系如图1所示[20]，图中s为拉普拉斯算子。为此，结合电压前馈解耦控制，提出了一种基于电流解耦的无源控制器新型设计方法，以消除互联矩阵中d轴电流与q轴电流的耦合关系，使得期望互联矩阵的未知参数由3个减少为1个，大大简化无源控制器的求解过程。

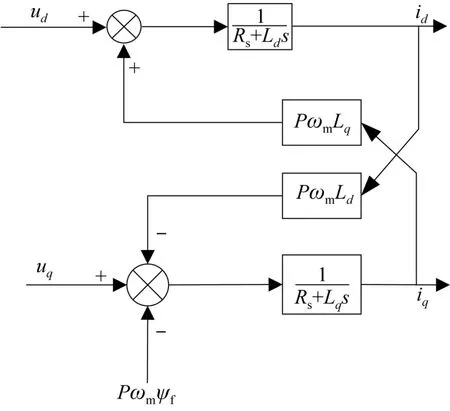
图1 表贴式永磁同步电机d轴、q轴电流的耦合关系Fig.1 Coupling relationship between d-axis and q-axis current of surface-mounted permanent magnet synchronous motor

电流解耦后表贴式永磁同步电机的数学模型可表示为：

3 实验验证

3.1 实验条件

为测试表贴式永磁同步电机的电流环在采用基于电流解耦的无源控制器时的响应带宽和转速响应特性，开展实验进行验证，并与电流环采用传统PI控制器时的结果进行对比。实验中选用的微处理器为STM32F407，电流环控制周期为125 μs，电流采样分辨率为12位，位置编码器的分辨率为17位。实验数据由微处理器采集，通过串口通信将所采集的数据传输给上位机。表贴式永磁同步电机测试平台如图2所示，该电机的基本参数如表1所示。

图2 表贴式永磁同步电机测试平台Fig.2 Test platform for surface-mounted permanent magnet synchronous motor

表1 表贴式永磁同步电机基本参数Table 1 Basic parameters of surface-mounted permanentmagnet synchronous motor

3.2 电流环响应带宽测试与分析

在永磁同步电机矢量控制中，电流环响应带宽是衡量控制器的一个重要指标：响应带宽越高，控制性能越好。为测试表贴式永磁同步电机的电流环在采用基于电流解耦的无源控制器时的性能，开展响应带宽测试，并与采用传统PI控制器的响应带宽进行对比。其中，电流环采用无源控制器时给定转速设定为额定转速1 000 r/min，阻尼系数r1=r2=1；采用传统PI控制器时，其参数Kp、Ki通过自整定方式得到。

电流环响应带宽测试方法如下：输入信号为q轴的正弦电流，其幅值为5 A，频率分别为100，200，250，333 Hz。通过测试得到不同频率下的q轴电流响应曲线，结果分别如图3至图6所示。不同频率下q轴电流响应的幅值衰减（输出信号与输入信号的幅值之比）和相位滞后如表2所示。

图3 频率为100 Hz时q轴电流响应曲线对比Fig.3 Comparison of q-axis current response curve with frequency of 100 Hz

图4 频率为200 Hz时q轴电流响应曲线对比Fig.4 Comparison of q-axis current response curve with frequency of 200 Hz

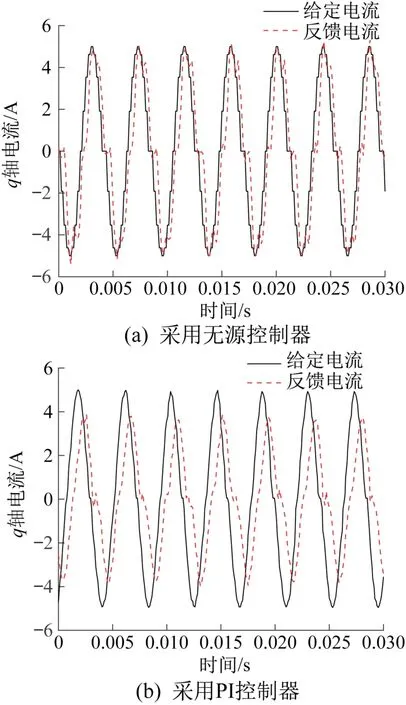
图5 频率为250 Hz时q轴电流响应曲线对比Fig.5 Comparison of q-axis current response curve with frequency of 250 Hz

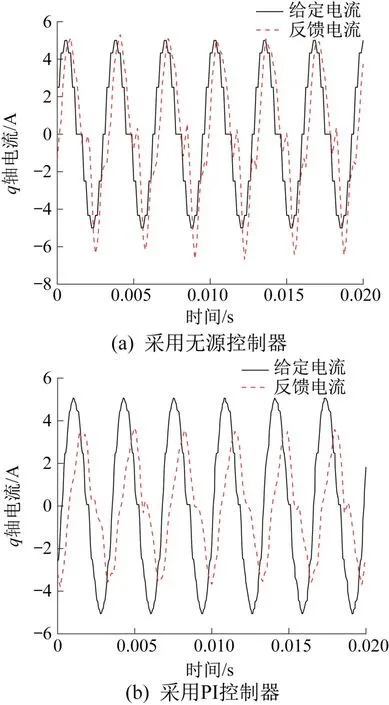
图6 频率为333 Hz时q轴电流响应曲线对比Fig.6 Comparison of q-axis current response curve with frequency of 333 Hz

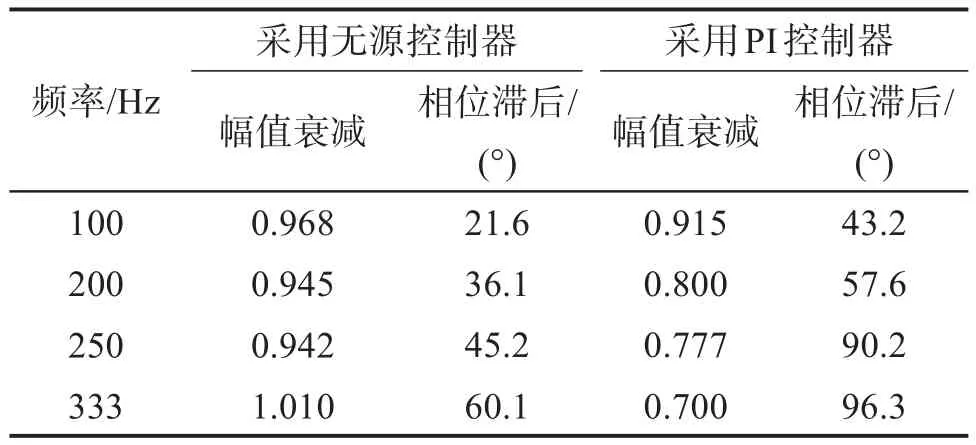
表2 不同频率下q轴电流响应的幅值衰减和相位滞后Table 2 Amplitude attenuation and phase hysteresis of qaxis current response at different frequencies

由实验结果可知，随着输入电流频率的逐渐增大，电流环采用基于电流解耦的无源控制器时q轴电流响应的幅值衰减和相位滞后均小于采用传统PI控制器时的，响应频率由小于250 Hz增大为大于333 Hz。

3.3 转速响应测试与分析

为测试电流环响应带宽提高对速度环的影响，分别在给定转速为500，1 000 r/min下开展转速响应测试及负载突变时的抗干扰能力测试。其中，负载扰动为表贴式永磁同步电机平稳运行后突增3 N·m负载。当表贴式永磁同步电机的速度环采用传统PI控制器，电流环分别采用基于电流解耦的无源控制器和传统PI控制器时，不同给定转速下的转速响应测试结果如图7和图8所示，转速响应的动态特性如表3所示。

图7 给定转速为500 r/min时的转速响应曲线对比Fig.7 Comparison of speed response curves with given speed of 500 r/min

图8 给定转速为1 000 r/min时的转速响应曲线对比Fig.8 Comparison of speed response curves with given speed of 1 000 r/min

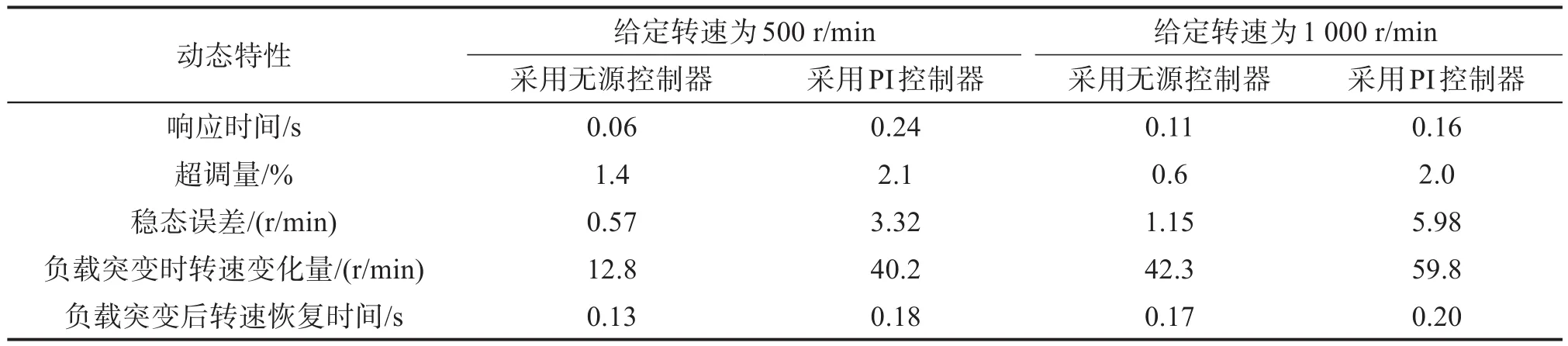
表3 不同给定转速下转速响应的动态特性对比Table 3 Comparison of dynamic characteristics of speed response under different given speeds

由实验结果可知，表贴式永磁同步电机的电流环采用基于电流解耦的无源控制器时，其转速响应时间、超调量、稳态误差和抗干扰能力均优于采用传统PI控制器时的。

4 结 论

针对在基于PCHD的表贴式永磁同步电机无源控制器设计过程中，因d轴、q轴电流存在耦合而导致期望互联矩阵未知参数过多的问题，提出了一种基于电流解耦的无源控制器新型设计方法，使期望互联矩阵的未知参数由3个减少为1个，并通过实验进行了电流环响应带宽测试和转速响应测试。实验结果表明，当表贴式永磁同步电机的电流环采用基于电流解耦的无源控制器时，其具有更高的电流环响应带宽，且转速响应时间、超调量、稳态误差及抗干扰能力均优于采用传统PI控制器时的。但是，无源控制器是基于永磁同步电机各参数间的物理关系计算得到的，对准确识别参数的要求较高。后续将结合参数在线辨识方法，针对永磁同步电机运行过程中参数变化对系统性能的影响进行研究。