铁路电气化接触网硬横跨的力学性能分析研究

陈 成

（中铁建电气化局集团南方工程有限公司，湖北 武汉 430223）

1 研究背景

电气化接触网硬横跨是高铁正常运行的关键设施，是一种门式桁架结构。它与硬横跨连接的悬挂设备、支持设备悬挂电力导线共同作用，为高铁运行提供动力[1]。硬横跨的立柱和横梁采用框架式结构，通常由角钢组装而成。硬横跨具有良好的刚性和耐磨性，在国内外的高铁建设中得到广泛应用[2]。硬横跨的结构稳定性对保证列车稳定运行具有至关重要的作用。因此，对硬横跨的力学性能进行分析有重要的意义。本文对硬横跨结构建立数学模型，运用一阶弹性分析法和二阶弹性分析法，计算各点的弯矩和集中力（剪力），分析其力学性能，为硬横跨的优化设计提供参考。

2 电气化接触网硬横跨力学模型

电气化接触网的硬横跨由两侧的立柱和中间的横梁连接而成，为了保证高铁正常运行，横梁上搭载悬挂设备、支持设备和测量仪器等[3]。立柱和横梁是硬横跨的主要承载结构。为了简化运算，本文忽略横梁上其他设备的尺寸影响，仅考虑横梁和立柱。悬挂设备、支持设备和测量仪器等的自重载荷，按照均匀载荷附加到横梁上处理。横梁主要承受弯矩和集中力；两侧的立柱主要承受轴向力、弯矩和集中力。图1为硬横跨的结构简图。

图1中，横梁的自重载荷qc包括横梁自重、悬挂设备和支持设备等的自重，本文选择常用的尺寸为80 mm×80 mm×8 mm的Q235B角钢建立模型，横梁自重按200 kg/m考虑，qc=2 kN/m。横梁的抗弯刚度E·I=151.4 kN·m2。

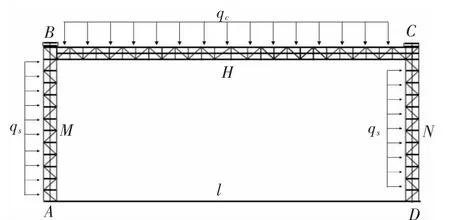
图1 硬横跨的结构简图

立柱部分高度为9 m，立柱角钢采用尺寸为100 mm×100 mm×10 mm的Q235B角钢连接而成，立柱自重按1 500 kg计算。设计最大风速为40 m/s，考虑最不利条件，假定风向垂直向右，风载荷qs按12 kN/m计算。立柱的抗弯刚度E·I=370.8 kN·m2。

3 硬横跨结构力学分析计算

结构的力学性能分析通常采用极限状态设计法，将研究对象视为理想材料，符合胡克弹性定律[4]。对于横梁，不考虑轴向力，两端只承受弯矩和集中力的作用；对于立柱，则考虑两端接点处的集中弯矩、集中轴向力和集中力的作用。

3.1 一阶弹性分析法

一阶弹性分析法，不考虑研究对象本身的微小变形，按照未变形的几何模型建立力学平衡方程，分析研究对象的受力情况及位移情况。假定转角和位移为未知量，通过接点处的平衡建立力学平衡方程，进而求出横梁和立柱的端点及中点所承受的弯矩和集中力。转角和弯矩取顺时针方向为正值；轴向力以受拉为正；集中力以向右为正。图2为硬横跨的立柱受力分析简图（为了方便绘图，将立柱横放）。横梁的受力分析与之类似，区别为左端的固定方式不同。

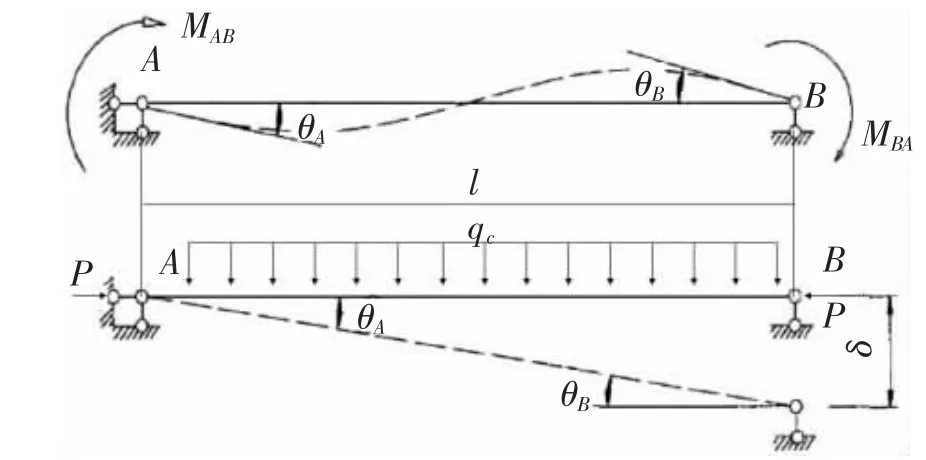
图2 硬横跨的立柱受力分析简图

由图2可知，立柱两端在力矩的作用下，将产生转角θA和θB。同时，立柱的右端由于侧向载荷而会产生较小的竖直方向的位移（竖向位移）δ，同时产生转角。由于实际的立柱受到两种作用的叠加，因此立柱转角的表达式为

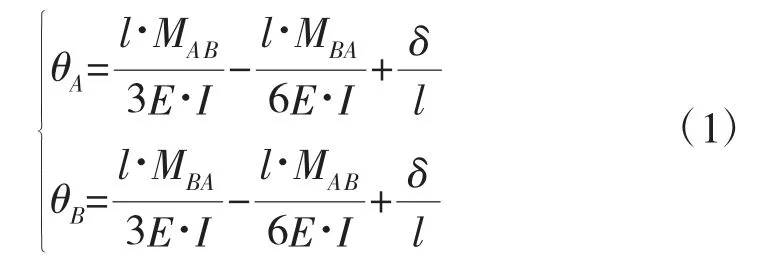
式中：l为立柱的长度，若是求解横梁的转角，则应代入跨距；MAB、MBA为作用在立柱两端的集中力的力矩；E·I为抗弯刚度；δ为构件竖向位移。

根据A、B点的平衡关系，得出弯矩和集中力与转角θA、θB以及竖向位移δ的关系为

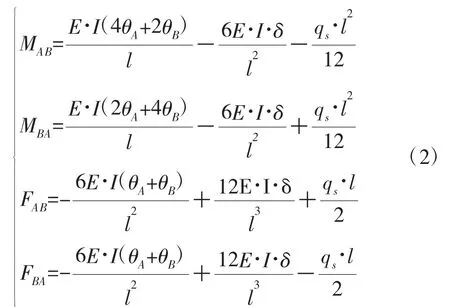
式中：qs为风载荷，若求解横梁的受力情况，应代入横梁自重载荷；其他参数符号含义同上。

根据边界条件，两个立柱的固定点处转角为零。分别取立柱或横梁作为分析对象，建立力学平衡方程组，利用计算机求解，即可得出立柱和横梁端点以及中点的弯矩和集中力。

3.2 二阶弹性分析法

二阶弹性分析法，需要考虑立柱的侧向位移和挠度。侧向位移会增大立柱接点处的弯矩，而挠度会增加立柱中间处的弯矩。

进行二阶弹性分析时，上述对于刚性材料的假设仍然成立。依旧假定硬横跨的转角和位移为未知量，此时应考虑横向载荷P的作用。受弯矩和横向载荷的作用，立柱产生侧向位移和挠曲变形，考虑这两种变形后的立柱转角的表达式为

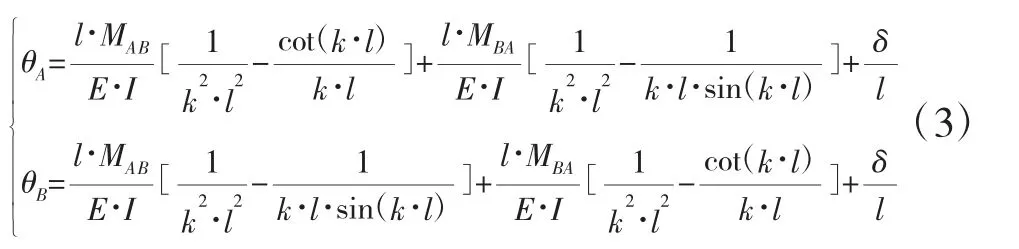
将式（3）代入式（2），可得二阶弹性分析法的弯矩和集中力的表达式。计算过程复杂，利用计算机求解。

3.3 算例验证

选定硬横跨跨距分别为21m、31 m、41 m这3种常用的跨距进行计算，分别得到4个端点A、B、C、D，3个中点M、N、H的弯矩和集中力，进行分析讨论。

一阶弹性分析法计算得到弯矩数据（见表1）和集中力数据（见表2）；二阶弹性分析法计算得到弯矩数据（见表3）和集中力数据（见表4）。

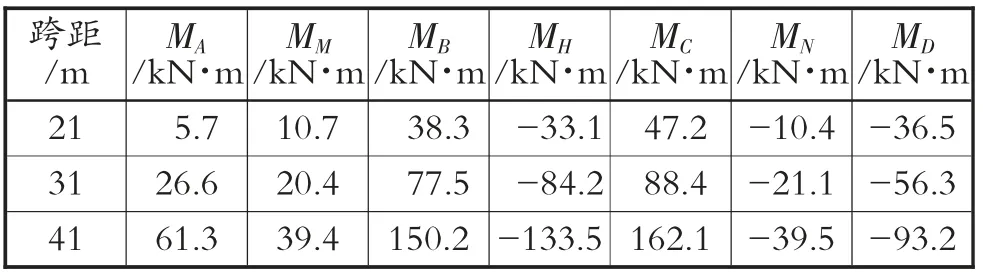
表1 一阶弹性分析法算例的弯矩数据

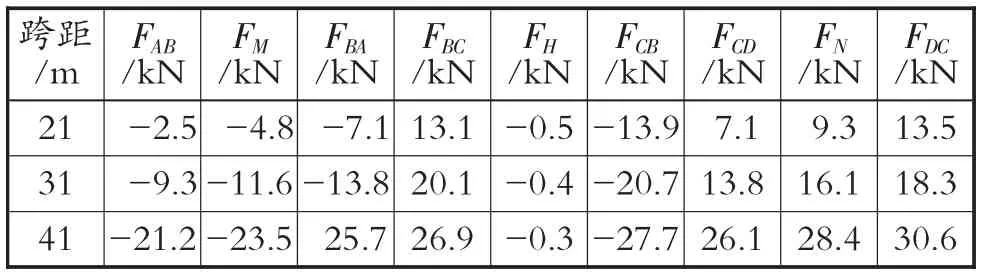
表2 一阶弹性分析法算例的集中力数据

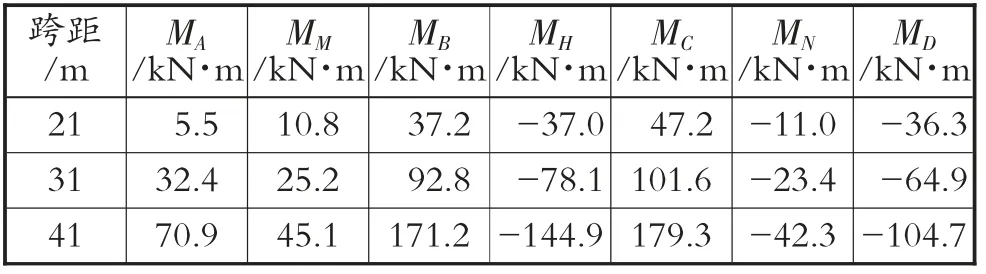
表3 二阶弹性分析法算例的弯矩数据

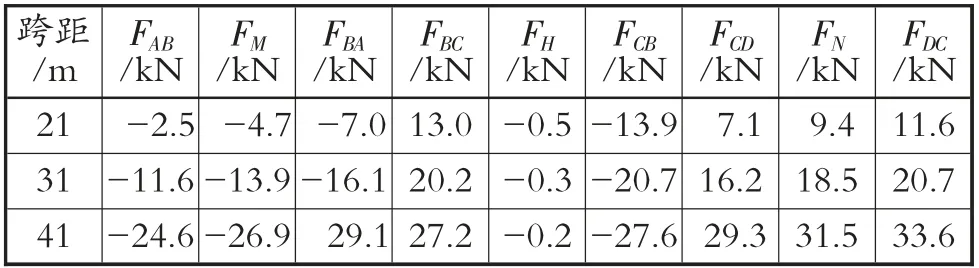
表4 二阶弹性分析法算例的集中力数据

将表1～表4中41 m跨距的数据绘制成折线图，见图3。将表3和表4中不同跨距条件下的数据绘制成折线图，见图4。为了对比分析，绘制折线图时，忽略弯矩和集中力的方向，所有数值取绝对值。

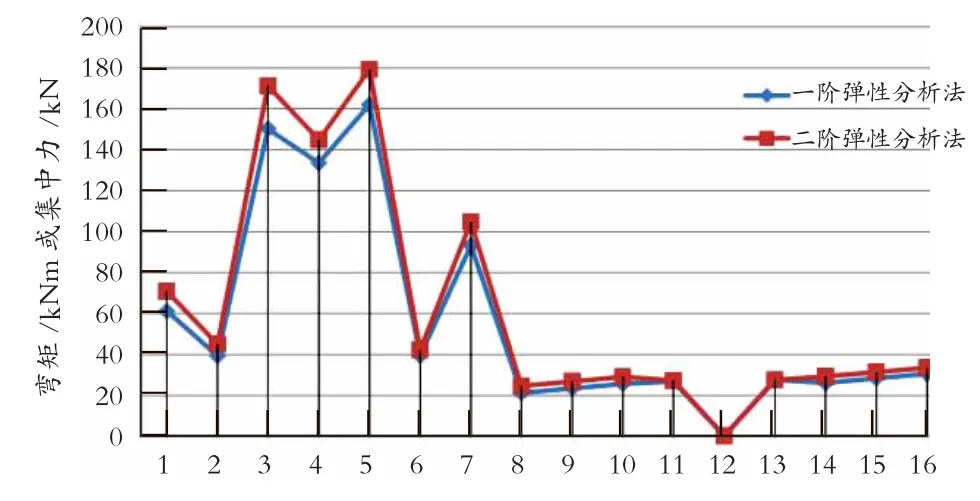
图3 一阶弹性分析法和二阶弹性分析法在41 m跨距时的对比折线图

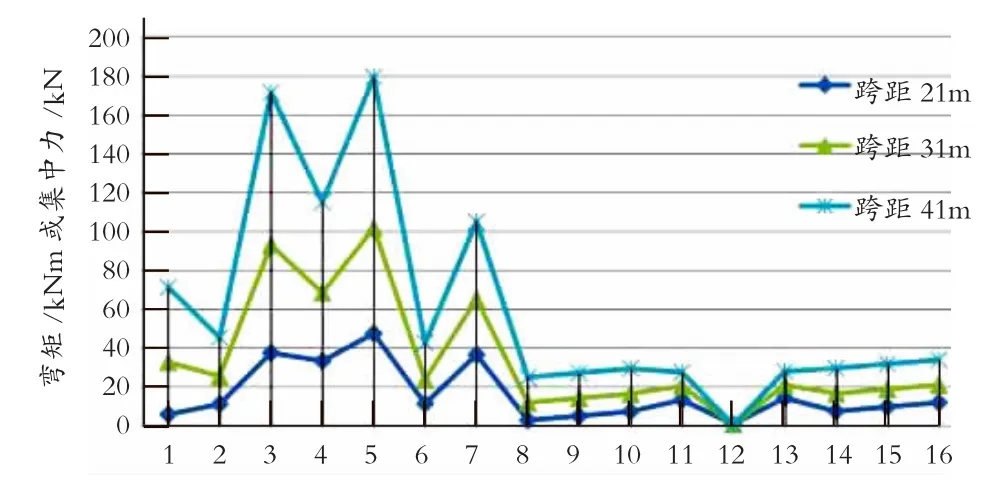
图4 不同跨距的受力情况对比折线图

由表1～表4的数据可知，随着硬横跨的跨距增大，各点处的内力呈增大趋势，立柱与横梁的接点处的表现最为明显。立柱和横梁的中点位置的弯矩和集中力均较小。

由表1～表4对比可知，一阶弹性分析法和二阶弹性分析法得到的力学性能变化规律具有一致性。由图3可知，二阶弹性分析法得到的受力分析数据，比一阶弹性分析法略大，表明二阶弹性分析法更符合硬横跨的实际受力情况。而且，两种弹性分析法在同一点的数值差距，随着硬横跨跨距的增加而呈现增大的趋势，对于大跨距的硬横跨，其实际受力情况较复杂，仅用一阶弹性分析法，难以达到理想的分析效果。

4 结论

电气化接触网硬横跨的结构稳定性对保证高铁正常运行至关重要，分析其力学性能具有重要意义。本文对硬横跨结构建立了力学模型，运用一阶弹性分析法和二阶弹性分析法，计算并验证了硬横跨各点的弯矩和集中力。结果表明随着硬横跨的跨距增大，各点处的内力呈增大的趋势，在立柱与横梁的接点处的表现最为明显；一阶弹性分析法和二阶弹性分析法得到的力学性能变化规律具有一致性；但二阶弹性分析法得到的数据比一阶弹性分析法得到的数据略大，更符合硬横跨实际受力情况。