引汉济渭二期高地下水位盾构隧洞渗流应力耦合研究

董 鹏， 李唱唱， 王正中， 刘 彪， 刘铨鸿， 马清瑞

(1.陕西省引汉济渭工程建设有限公司， 陕西 西安 710024； 2.西北农林科技大学 水利与建筑工程学院， 陕西 杨凌 712100)

1 研究背景

引汉济渭工程是由汉江向渭河关中地区调水的省内南水北调骨干工程，是缓解近期关中渭河沿线城市和工业缺水问题的根本性措施，总投资199.06×108元。工程位于黄土高原地区，其中白鹿塬段洞身最大埋深为300 m，洞顶最大水头为222.02 m，在国内无类似工程可参考。大埋深、高水头的黄土盾构结构设计是工程安全施工、运营的关键。

盾构法施工已有近200年的历史，是我国地下工程中一种重要的施工方法。盾构可分为机械式盾构、半机械式盾构、手掘式盾构、网格式盾构、挤压式盾构，其中机械式又分为泥水加压式盾构、土压平衡式盾构、局部气压式盾构。如今盾构法的施工变得更加机械化，施工对地层的要求较低，即在土质差、水位高的工况下也能通过盾构法修建埋深较大的盾构隧洞，其施工具有较高的技术经济优越性[1]。

盾构隧洞的施工过程包含4个阶段，分别为挖土阶段、盾尾注浆阶段、盾尾脱开阶段和固结沉降阶段，各阶段的科学、合理概化是盾构隧洞施工仿真的关键。其中，生死单元法是通过单元的“生”或者“死”来模拟材料对系统整体的贡献程度，被证明能有效模拟隧洞挖土过程，并且已被国内外许多工程实践证明其可靠性[2-11]。同时，应用有限元生死单元法，能较为准确地预报隧洞开挖过程的围岩卸载以及地表固结沉降变形等演变规律[12-17]。区别于矿山法，隧洞盾构施工过程会在盾尾产生一定的空隙，称为盾尾脱空。盾尾脱空对盾构法施工衬砌结构的应力变形影响显著[18-19]，是隧洞盾构施工仿真模拟的难点和重点。张海波等[20]应用Goodman单元模拟了盾构前行、盾尾脱空及注浆；丁文其等[21]采用注浆材料变刚度等效法模拟了注浆材料的凝固过程，为盾尾注浆模拟提供了参考。此外，围岩的本构关系是围岩以及衬砌结构变形应力准确预报的核心，为偏安全多采用弹塑性本构模型[12, 22]。西安市地铁施工的仿真研究结果表明[23]，基于摩尔库伦(Mohr-Coulomb)准则的弹塑性模型适用于西安黄土高原地区地下空间开挖模拟研究。但西安地铁工程的研究成果多未考虑地下水的作用，且其埋深一般在200 m以内。200～300 m埋深高地下水位黄土地区盾构施工相关研究较少。

引汉济渭二期工程中白鹿塬隧洞处于高地下水且地质条件复杂的砂砾岩、泥岩环境中，该工程在国内外非常罕见，缺乏工程经验、相关理论和设计方法，采用盾构法对该段隧洞施工的安全性不明确。其中，高地下水复杂地质条件下围岩与衬砌相互作用机制及其承载力、抗裂能力更是盾构法施工的关键指标。基于此，本文以该工程为依托，采用有限元法建立盾构隧洞三维渗流-应力耦合有限元模型，应用生死单元技术开展洞段三维动态掘进过程的模拟，重点分析高埋深、高地下水位作用下盾构掘进过程中围岩孔隙水压力、围岩与衬砌结构的受力变形等变化规律，为引汉济渭工程的安全运营提供参考依据。

2 隧洞渗流-应力全耦合模型

2.1 围岩水动力学方程

考虑渗流时，渗流体积力以地下水在孔隙内的流动为主，通常为层状流动，且符合达西(Darcy)定律[23]。假设土体为均值材料，Darcy定律认为通过介质中单位面积的自由液体的体积速率vw与水头的梯度成正比，即：

(1)

式中：k为介质的渗流系数，m/s；h为水头，m，l为渗径，m。

由质量守恒定律可得非饱和土的渗流连续方程：

(2)

式中：Q为源汇项，kg/(m3·s)；Cm为比水容重，其值为土-水特征曲线斜率的绝对值，m-1；z为重力方向空间坐标，m；t为时间，s;εv为围岩的体积应变。

渗透系数k为饱和度和材料孔隙比的函数。对于一个特定的液体而言，它在给定的孔隙介质中的渗透系数依赖于介质中该液体的饱和度，假设这种依赖是可以分离开的，即

k=krks

(3)

(4)

式中：ks为围岩的饱和渗透系数，m/s；kr为折减系数，是饱和度Se的函数，当完全饱和即Se= 1.0时，有kr= 1.0。

2.2 应力应变方程

假设围岩、衬砌以及砂浆等材料均为各向同性材料，其力学平衡方程可用下式表示：

σ′ij+Fj=0

(5)

根据有效应力原理，孔隙水作用下的岩体本构方程为：

σ′ij=Dijklεkl-αρwghδij

(6)

几何方程为：

εij=(Ui,j+Uj,i)/2

(7)

式中：σij为应力张量，Pa；σ′ij为有效应力张量，Pa；εij为应变张量；Fj为体积力，Pa；Dijkl为弹性模量张量，Pa；h为孔隙水压力，m；α为Biot系数，Pa-1；δij为Kronecker常数；Ui为固体位移，m。

2.3 围岩屈服准则

摩尔-库伦模型对岩体从受力到变形破坏均有较好的计算效果，尤其是对岩体稳定及卸载分析上特别有效[24]。摩尔-库伦模型破坏有拉伸破坏准则，当发生剪切破坏时，遵守非关联的流动法则，拉伸破坏时，满足相关联的流动法则[25]。Mohr-Coulomb准则不仅能较好地反映岩土材料拉压不等的特性，同时模型简单易用，已成功应用于富水地区黄土隧道的地层变形控制[25]、西安地区地裂缝区段黄土地铁隧道开挖模拟[26]和西安地区黄土、古壤土层中盾构施工模拟[27]以及高埋深(埋深170 m)软岩隧道土体开挖变形模拟[28]。

基于此，本文中黄土围岩的屈服准则采用Mohr-Coulomb准则[6,29-30]。摩尔-库伦模型的屈服面函数可以表示为：

F=Rmcq-ptanφ-c=0

(8)

其中：

(9)

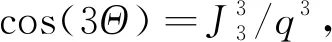
2.4 隧洞施工模拟实现方法

本文应用大型有限元商业软件ABAQUS实现隧洞开挖的数值仿真以及影响参数分析。通过单元“生死”实现盾构施工连续掘进的动态开挖模拟，得出隧洞开挖过程渗流场、应力场、位移场以及衬砌的受力动态演变规律。盾构施工过程的动态模拟采用刚度迁移法来完成。即在盾构隧洞的盾首以及盾尾提前设置盾构、衬砌、砂浆等单元，并通过单元激活和杀死的手段进行单元刚度的变化。

把盾构推进的过程当作非连续的过程进行研究，盾构隧道每次前进的距离为一个管片单元的宽度，盾构前进时需要进行单元材料的变换；每顶进一环，盾首前方的开挖面土体单元和预设单元变换为盾构单元和超开挖间隙单元，盾构壳尾部单元变为盾尾孔隙单元；而盾尾孔隙单元变为注浆单元，同时朝开挖方向激活1环管片单元[31]。根据实际施工过程，为了减小边界对计算的影响，将主要研究位置放在整个模型的中部位置并模拟开挖过程，每个长度是一个管片长度[32]。

3 引汉济渭二期隧洞有限元模拟

3.1 工程概况

引汉济渭二期输配水工程是引汉济渭工程的重要组成部分，输水区域东西长约163 km，南北宽约84 km，总面积约为1.4 km2。其中南干线全长102.07 km，主要穿越秦岭岭北中低山区、山前洪积扇区、河谷阶地、黄土台塬四大地貌单元，出露地层主要为下元古界宽坪群变质岩、燕山期花岗岩、新近系沉积岩及四系松散堆积层。地下水以基岩裂隙水、第四系松散岩类孔隙水、新近系碎屑岩类裂隙孔隙水为主。

南干线输水线路总长102.07 km，起点黄池沟配水枢纽水位为514.88 m，末点灞河分水口要求水位为470.00 m，水面高差为44.88 m。白鹿塬隧洞(4#隧洞段)位于南干线桩号78+000～90+735处，线路长9.37 km，埋深一般在140～300 m，隧洞均为明流长洞。隧洞进口位于浐河东岸，长安区鸣犊镇狮村三村东侧；出口位于灞河西岸，灞桥区灞陵乡寇家村北侧。设计洞底起点高程为472.663 m，末点高程为469.540 m；设计起点水位为475.78 m，末点水位为472.66m。隧洞洞室围岩为泥岩夹砂岩，采用盾构法施工，隧洞断面为圆形，内径4.40 m。盾构段衬砌采用预制C50钢筋混凝土管片，管片环分为6块，内径4.40 m，环宽1.20 m，管片厚0.35 cm，采用错缝拼装。隧道计算断面选择隧道埋深最深处S4Z-2，地表至隧道顶部的距离为282.22 m，地下水面至隧道顶部的距离为222.02 m。隧洞为泥岩、砂砾岩隧洞，隧洞上部为Q3～Q1风积、风洪积地层，洞身主要为新近系泥岩、砂砾岩，隧洞Ⅳ类围岩长度为2 440 m，约占26.04%；Ⅴ类围岩长度为6 930 m，约占73.96%。隧洞基本位于地下水位以下。隧洞进口段黄土塬边冲沟发育，沟坎陡立，斜坡稳定性较差，开挖前应做好防护及防排水措施。出口段洞身可能会达到极限欠稳定状态。

由于洞段在无地下水的情况下稳定性相对较好，位于地下水位以下时围岩自稳性差。隧洞大部分洞段位于地下水位以下，饱和度大于80%，处于饱和状态。由于泥岩隧洞成洞条件十分困难，隧洞施工开挖后，其围岩稳定性极差，自稳时间很短。考虑到地表有村落房屋等建筑物，在高地下水位的泥砂岩洞段，采用常规钻爆法施工风险极高。而采用盾构法施工，具有施工安全性高、掘进速度快、地层适应性强、环境影响小、地表沉降小等显著优点。因此，项目拟采用盾构法施工。

3.2 有限元模型的建立

3.2.1 几何尺寸 本文取引汉济渭二期白鹿塬隧洞最大埋深洞段S4Z-2为研究对象。隧洞埋深取282.22 m，地下水位取222.02 m。结构尺寸的初步设计方案为：盾构机长为3.60 m，盾构外径为2.21 m，管片宽度为1.20 m；衬砌的厚度为0.35 m，注浆层厚度为0.15 cm；隧洞开挖半径为2.20 m；预制混凝土管片混凝土强度等级为C50。为消除边界效应和准确反映衬砌结构的真实受力变形特征，本文取隧洞模拟开挖段36 m，即模拟30步的盾构掘进过程。此外，根据圣维南原理，模型沿轴线方向(y向)前后各取18 m，洞顶与洞侧范围约取7.5倍洞径，即模型长72 m，宽30 m，高60 m。有限元模型中取隧洞圆心为坐标原点o，y正方向为开挖方向，z负方向为重力方向。本文在隧洞开挖仿真时，为消除模型边界的约束影响，沿隧洞轴线方向共设置3个控制段，见图1。3个控制段包括已开挖段(0≤y<18 m)、开挖模拟段(18m≤y<54 m，相当于30个开挖分析步)和预留不开挖段(54m≤y≤72 m)。在初始地应力场平衡分析后，已开挖段通过“生死单元”技术将该段内的岩体单元去掉，衬砌对应的位置用管片混凝土、注浆混凝土材料代替。在此基础上，在已开挖段的掘进前缘置放盾构机并开始30个开挖步的模拟。此外，为了进一步提高计算结果的合理性，选择开挖段的中间断面(图1中的A-A断面，后称“参考断面”)作为代表衬砌，分析开挖过程管片的外水压力、受力变形演变规律。

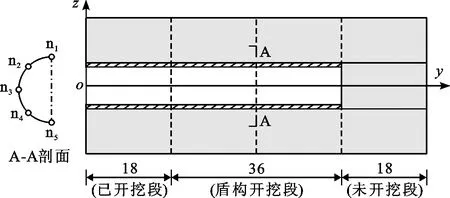
图1 隧洞开挖模拟边界控制及参考面选取示意图(单位：m)

在进行模拟单元剖分时，为兼顾模型求解的精度和计算成本，综合考虑模型几何特征、收敛和精度，采用“疏密技术”对模型不同部位进行不同精细程度的单元划分[33]。衬砌、注浆层沿厚度方向分别取2层和1层单元；隧洞径向2.5倍半径范围内采用渐变网格；纵向间距取一个管片宽度；模型共35 280个单元，33 547个节点。隧洞有限元模型的网格及主要尺寸见图2。岩土体采用ABAQUS渗流-应力耦合单元C3D8RP单元模拟，砂浆层、衬砌和盾构则采用C3D8R单元模拟。

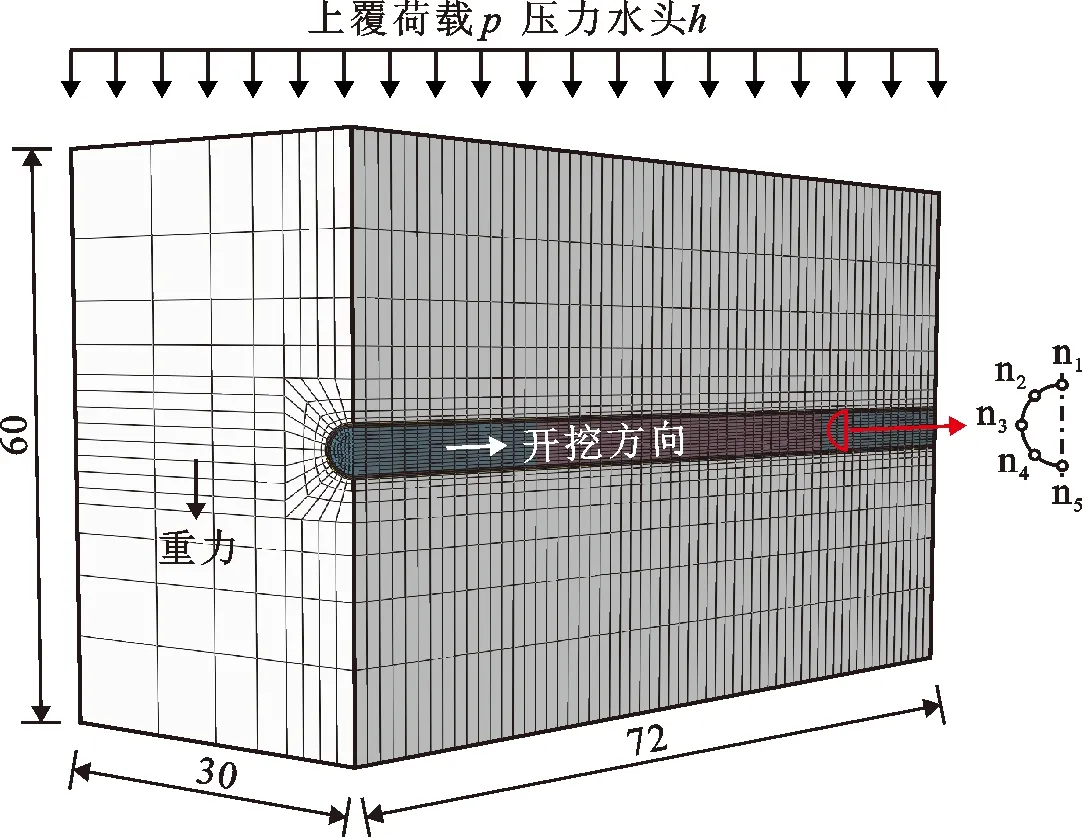
图2 隧洞有限元网格与主要尺寸示意图(单位：m)

3.2.2 边界条件 除模型上表面外，其余竖平面均设为不透水边界。x=0对称面设对称约束，除模型上表面外设法向定向铰支座约束。上边界设模型上覆土层的压力和孔压边界，按围岩覆盖厚度以及地下水位情况分别计算得到其总应力值为3.63 MPa、孔压值为1.94 MPa。综合考虑工程的安全性以及地下水的保护等因素，开挖过程不考虑排水作用，即开挖面与衬砌内径均为自由排水边界。

3.2.3 材料参数取值 研究洞段洞身围岩主要是泥岩，模型中假设其为均匀弹塑性体，可用Mohr-Coulomb本构描述；孔隙水服从Darcy定律。盾构机、注浆层以及衬砌视为弹性材料。按照工程典型洞段的土工试验结果，以及泥岩现有相关研究成果[28-29]，确定模型计算的参数，如表1所示。

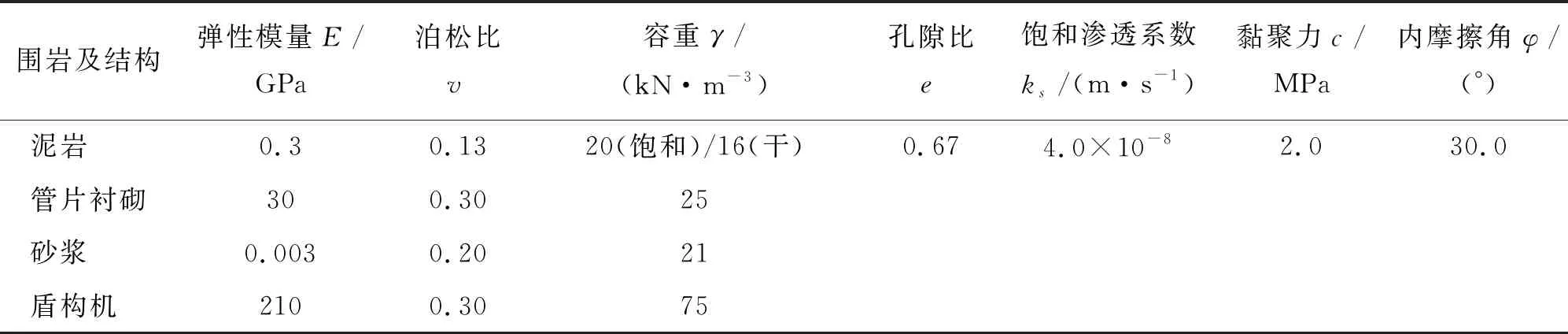
表1 计算所用的地层和材料参数

3.3 有限元仿真结果分析

3.3.1 渗流场计算结果 隧洞开挖前和结束时刻，模拟计算的围岩孔隙水压力变化情况见图3。由图3(a)可知，隧洞开挖前孔压在2倍洞径范围内引起显著的孔隙水压力重分布。洞周水压力分布关于洞轴线中心对称分布。洞顶与洞底的水压力远低于洞侧，洞顶水压力值约为0.98 MPa(98 m压力水头)、洞侧约为2.98 MPa(298 m压力水头)。模拟结束时刻，最小孔隙水压力出现在掌子面中心点处(图3(b))，其值约为1.44 MPa(144 m压力水头)。

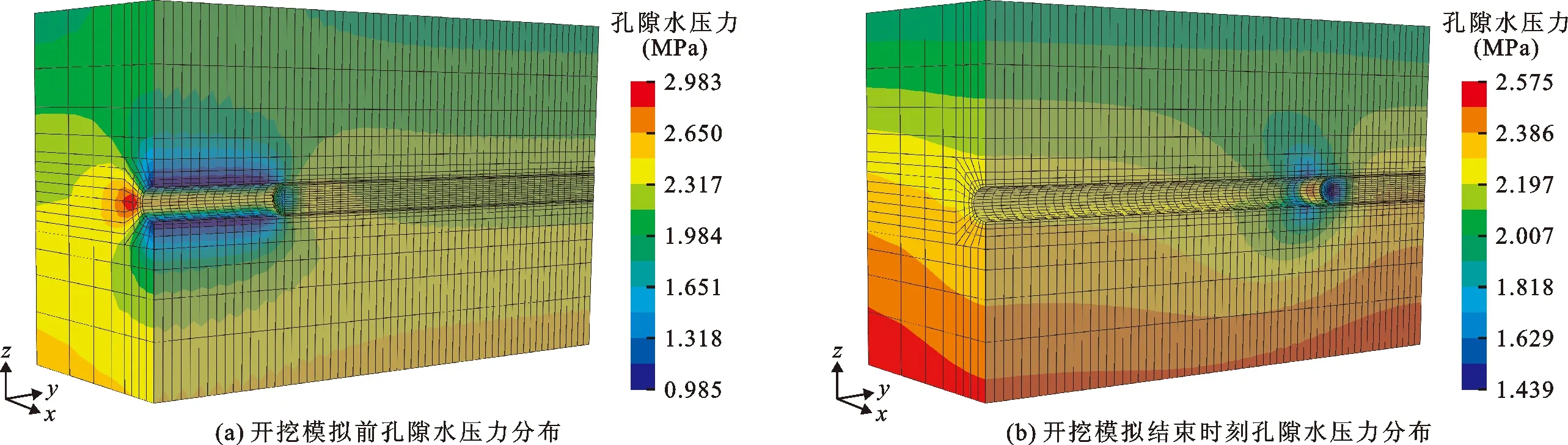
图3 隧洞开挖前和结束时刻围岩三维孔隙水压力分布

模拟结束时刻参考面(y=36 m)至掌子面的围岩孔压分布如图4所示。

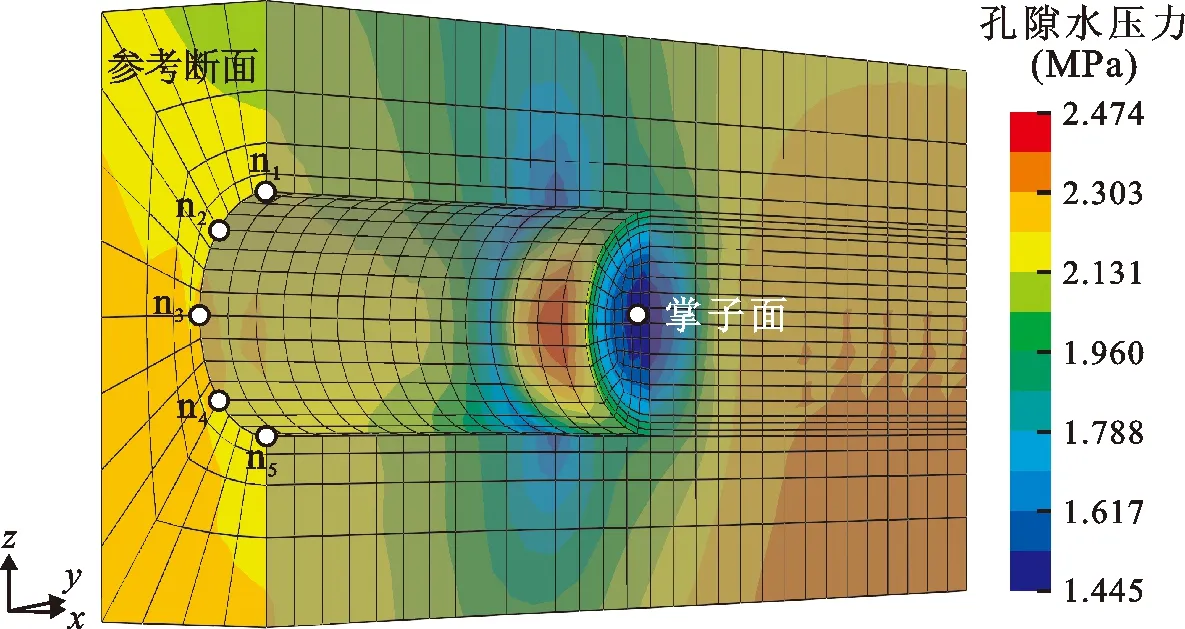
图4 开挖模拟结束时刻参考面-掌子面段孔压分布

由图4可见，在隧洞开挖面1倍洞径范围内发生了较大的孔压下降，最小孔隙水压力出现在掌子面中心处，其值约为1.44 MPa(144 m压力水头)。盾构机围岩受到盾构机的约束以及掌子面法向卸载变形的双重作用，出现了超孔隙水压力，最大值约为2.48 MPa(248 m压力水头)，超过原始状态(平均地下水位224.22 m)约0.24 MPa(24 m压力水头)。超孔隙水压力在盾构机后的1倍盾构机宽度范围内逐渐消散。

为具体分析开挖过程中隧洞轴线上水压力的变化规律，绘制参考断面特征点(见图4中参考断面的点n1～n5)孔隙水压力随开挖过程的变化，如图5所示。在图5中，下横坐标表示掌子面距参考断面的相对距离，负值表示掌子面向参考面开挖靠近的相对长度，其绝对值越小表示掌子面离参考断面越近；反之，正值表示掌子面离参考断面的相对长度，其绝对值越大表示距参考面越远。双横坐标用于识别参考面的相对位置以及开挖的绝对长度。通过图5对比不同分析步下洞周渗流场的分布情况可知，参考面不同部位的孔压变化曲线基本重合，表明洞周不同部位的孔压受其高程差的影响相对较小。洞周孔隙水压力的变化受开挖过程的影响显著，孔隙水压力随开挖过程先降低后回升，随后趋于稳定；孔隙压力等值线在纵剖面内出现较大的降落漏斗，降落漏斗中心距掌子面在-8～-10 m之间，远离掌子面时孔隙水压力有一定的回升。衬砌任一点外水压力值均随着开挖过程呈左高右低的V字形变化，最低点位于当前开挖步(为混凝土管片刚支护时)，其压力水头值为154.9～174.2 m，随着后续开挖则逐渐回升，当开挖距离距初始开挖点30 m时，孔隙水压力基本稳定在219.7～224.2 m水头。

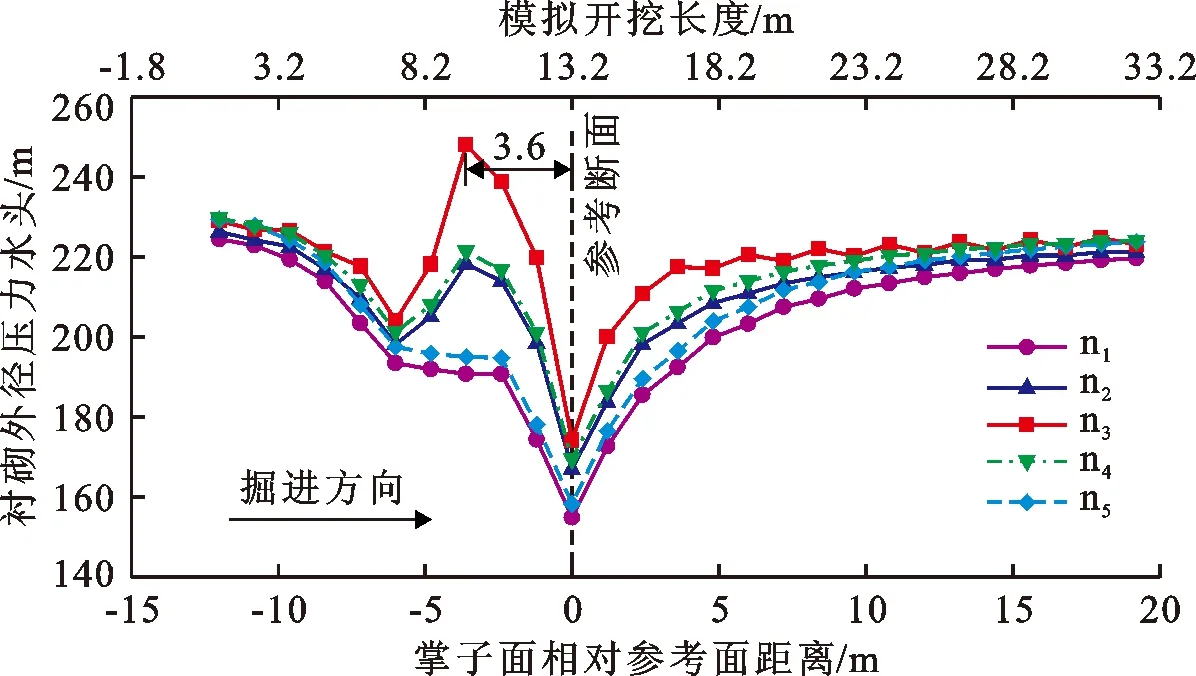
图5 参考断面围岩特征点压力水头变化过程线

特别地，在洞轴线上距离掌子面前缘3.6 m处出现超孔隙水压力，其孔压最大值约为248.0 m。由公式(2)可知，孔隙水压力的变化不仅与压力水头梯度有关， 而且与围岩的体积变形有关。根据热力学第二定律，压力梯度作用不会引起超孔隙水压力。故计算结果中超孔隙水压力主要是因为隧洞开挖过程掌子面前缘围岩体积压缩变形而引起的。随着掌子面离开并继续向前推进，围岩的应力将进一步释放、体积压缩变形减小，加之渗流作用使得超孔隙水压力逐渐消散。

3.3.2 应力变形场计算结果 图6和7分别为隧洞开挖后围岩的应力和应变计算云图(以拉应力为正)。隧洞开挖后，由于地应力重新调整，在隧洞周围发生应力集中现象，尤其是在隧洞洞侧最为明显。盾构机掘进使岩土体的应力场发生了改变。由图6可以看出，洞周以及隧洞开挖面前方一定范围内岩土体的主应力发生明显变化。由于地应力的释放，开挖后隧洞围岩附近最大主压应力约为7.145 MPa；最大主拉应力约为1.424 MPa。结合图7可知，应力和应变的变化基本上是以挤压区和卸载区的分界线为界。在模拟盾构的开挖过程中，盾构对周围地层的影响有显著的分区特点和规律性。应力和应变在洞周呈对称性分布。

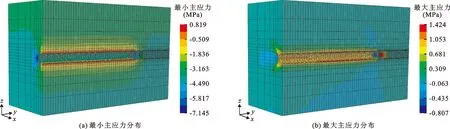
图6 隧洞开挖后围岩的主应力分布

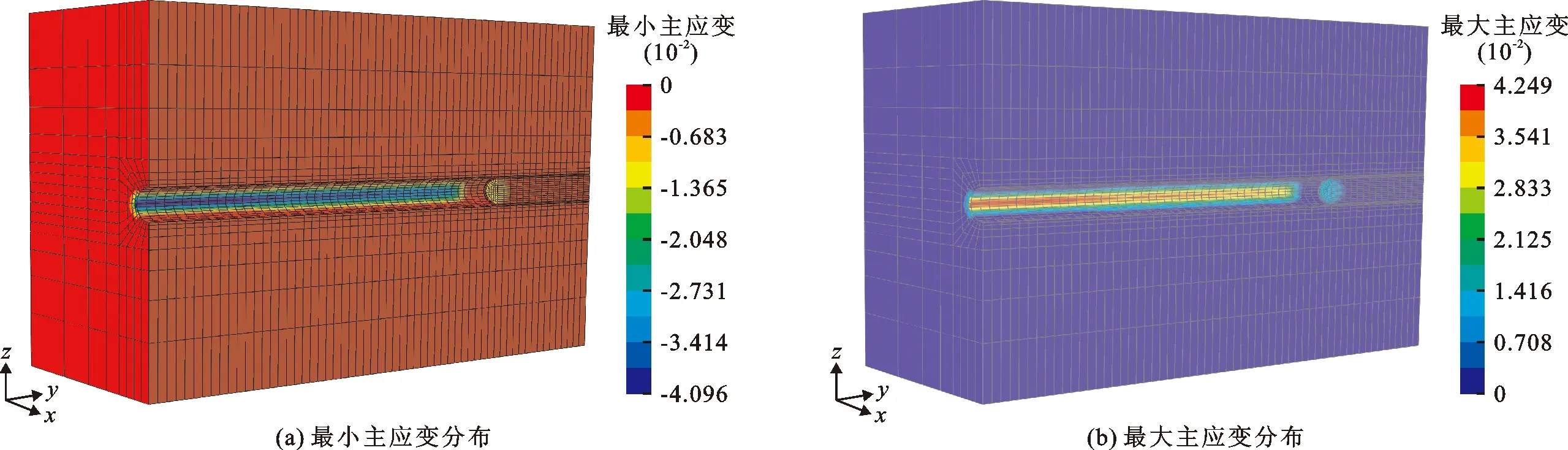
图7 隧洞开挖后围岩的主应变分布

3.3.3 围岩等效塑性应变分布 隧洞开挖后围岩等效塑性应变分布见图8。由图8可以看出，因开挖扰动，隧洞周围出现了较小范围的塑性区，塑性区主要在盾构开挖前缘以及洞侧土体；洞顶和底部未出现明显的塑性变形。表明该工程的隧洞采用盾构法施工时，盾构开挖前缘及洞侧围岩的失稳破坏是隧洞围岩的主要破坏模式。塑性应变沿轴向影响范围约为6 m，沿洞侧水平向的影响范围约为3 m，塑性区最大值分布在拱腰附近。

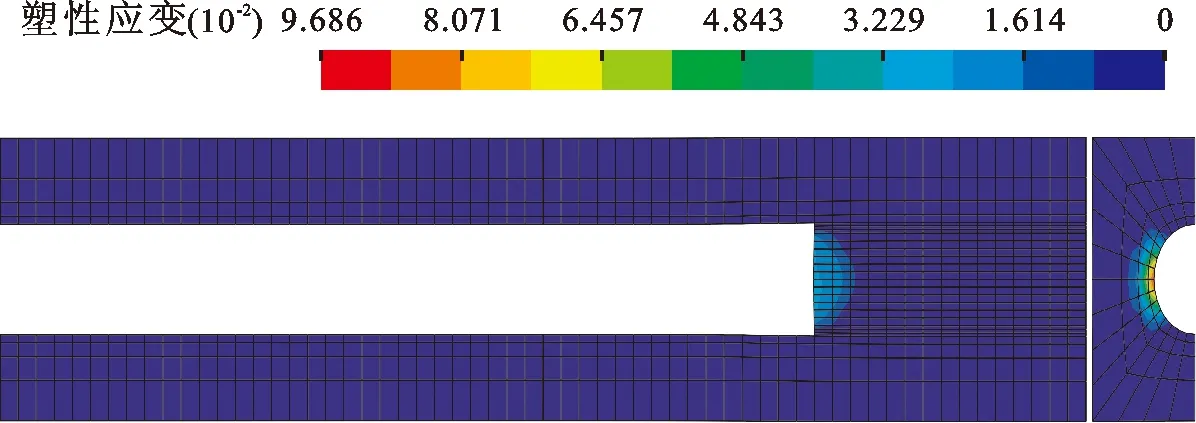
图8 隧洞开挖后围岩等效塑性应变分布

3.3.4 衬砌结构应力变形计算结果 隧洞开挖过程中断面各特征点衬砌内、外缘切向正应力随相对开挖长度的变化见图9。由图9可见，衬砌内、外缘基本属于受压状态；应力在支护后相对开挖长度为5 m的范围内变化相对明显，随后趋于稳定。数值上，外缘切向压应力值内径沿环向的变化范围约为外径的2倍；最大切向压应力和拉应力发生在边墙处,中其值分别为18.77、0.85 MPa, 小于C50混凝土的抗压强度设计值23.10 MPa和抗拉强度标准值1.89 MPa，即衬砌结构满足承载力和抗裂要求。

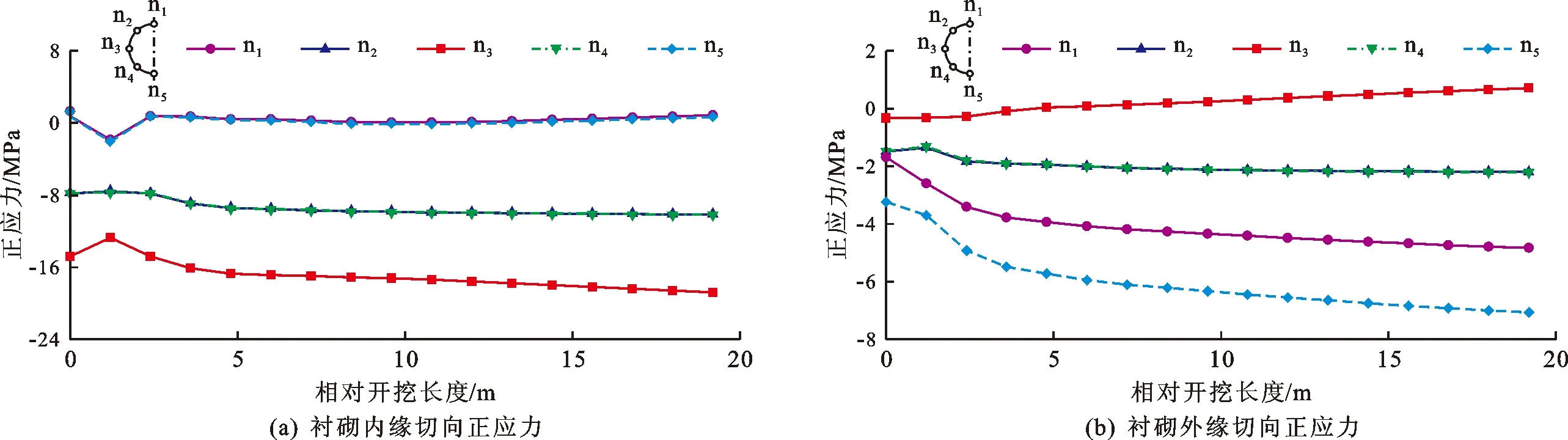
图9 隧洞开挖过程中断面各特征点衬砌内、外缘切向正应力变化(以拉应力为正)

以指向圆心的径向位移为负值，绘制隧洞断面各特征点衬砌的径向位移，如图10所示。根据图10中洞周位移分布情况，隧洞顶拱出现明显的径向收缩，而底部并未产生明显的径向变形，侧拱及拱腰处发生向外变形。由此可以判断，隧洞衬砌的变形为垂直向的上下挤压及洞侧向外变位。

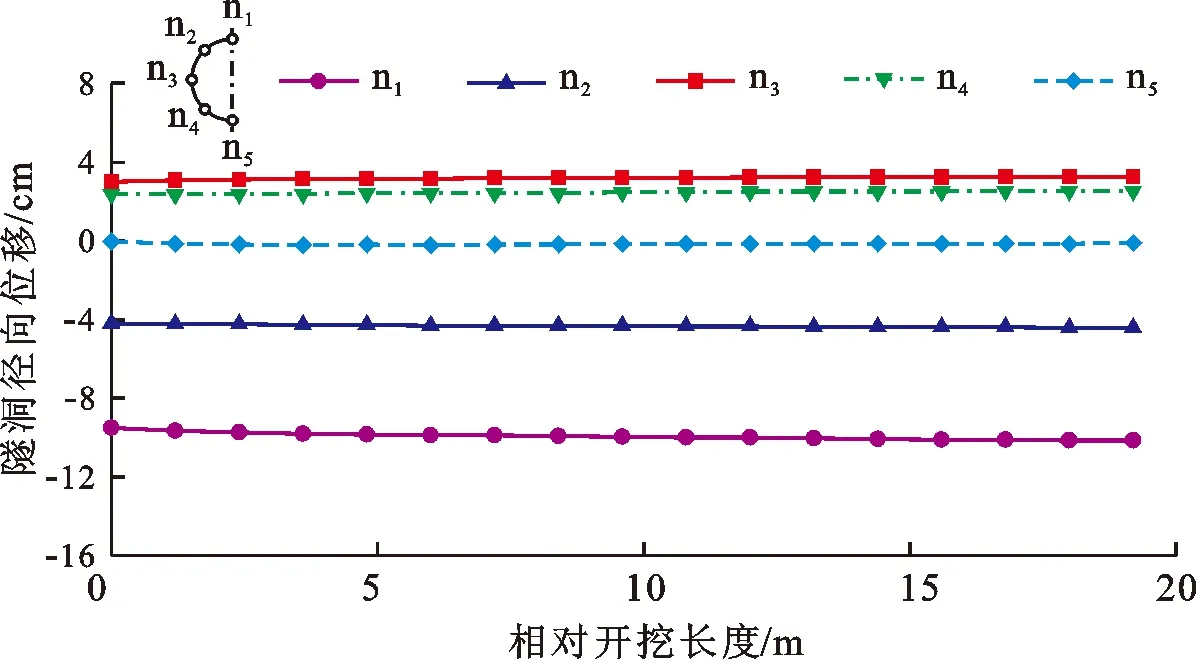
图10 隧洞开挖过程中断面各特征点衬砌径向位移变化

位移最大值发生在顶拱，约为-10.2 cm；侧拱处发生最大向外变位径向位移，其值为3.3 cm。衬砌整体径向位移在衬砌支护瞬时产生，随开挖过程无明显变化，表明衬砌结构具有较好的刚度，受后续掘进施工的影响可以忽略不计。

4 结 论

以引汉济渭二期工程南干线白鹿塬隧洞最大埋设洞段作为研究对象，采用ABAQUS渗流-应力全耦合数值模拟方法研究了隧洞0.35 cm衬砌、0.15 cm注浆设计工况下，开挖过程中围岩孔隙水压力、围岩应力变形以及衬砌应力变形的分布规律，主要结论如下：

(1)白鹿塬隧洞采用盾构法施工时，衬砌外缘孔隙水压力随开挖面靠近与继续推进呈先减小后增大的V型分布，随后趋于稳定；距离掌子面前缘约3.6 m的隧洞断面处会因围岩变形作用而引起超孔隙水压力，最大值约为248.0 m。

(2)隧洞围岩应力、应变、位移呈对称性分布；位移场表现出顶拱下沉，底拱隆起，最大位移发生在顶拱。侧拱处围岩等效塑性变形较顶拱和底拱明显，故侧拱的围岩失稳是围岩的主要破坏形式。管片内、外缘在施工时主要表现为受压状态，最大压应力为18.77 MPa。

(3)衬砌的受力变形在支护瞬间产生，随后的开挖掘进对衬砌的径向变位的影响可以忽略不计；衬砌内、外缘环向正应力随开挖步先减小后增加，增加幅度约为12%，随后稳定。环向正应力绝对值虽有所增加，但增幅不大，数值上满足C50混凝土的强度要求。