反例教学法在高中数学教学中的应用
江苏省梁丰高级中学
施冬芳
美国数学家盖尔鲍姆提出:“数学由证明和反例构成,并朝着证明与反例构造发展.”反例是指通过变换事物的属性,引发思辨,从反面凸显出事物的本质属性的例证.证明是通过已知为真来确定某一事物的真实性,反例则是用已知为真揭露另一个判断是虚假的,两者的目的都是为了揭露事物的本质属性,它们呈相辅相成的关系.
新课标明确提出:“数学教学应用实例进行合情推理,让学生在猜测、探索、演绎推理中确定结论的正确性,或构造反例来驳回错误的猜想.”反例的构造能凸显概念及定理的本质特征,让学生在反思中发现错误,加深对知识的理解与掌握程度;同时,构造反例还可打开学生的逆向思维,帮助学生从反面理解所学知识,培养学生解决问题的能力.
1 反例法在分类讨论中的应用
任何一个结论的成立都离不开一定条件的辅助,每种数学思想方法的应用也有其相应的范围.高中数学相对复杂,不少问题的结论并不唯一,分析时需根据问题的特点,从若干类出发,将一个大问题转化为一个个小问题.这种根据实际情况分类,再逐个突破研究的数学思想就是常见的分类讨论思想.
然而,当我们遇到的命题似真似假时,利用反证法常会出现分类不全或假设错误,导致解题失败.而反例的构造,则能凸显问题的本质,快速解决问题.解题中,学生常会遇到一些问题无法直接求解,此时巧妙地从问题的反面进行分析,可使问题变得更加简单.
例1已知关于x的方程x2+2ax+2a2-1=0至少有一个负实数根,则实数a的取值范围是什么?
解析:此题若从正面来论证,需分别从三种情况来分析.①存在两个负实数根;②正、负实数根各一个;③存在一个零根,一个负实数根.
若分别讨论以上三种情况,不仅过程繁琐、冗长,还容易出现失误.本题若构建反例,设方程无负实数根时实数a的范围为A,则方程至少有一个负实数根时a的范围即为A的补集.
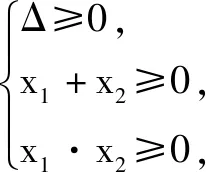
点评:本题若从正面论证,需耗费大量的时间与精力,而从反例的角度去分析,则使繁杂的问题变得简捷很多.因此,遇到分类讨论的问题时,不要受思维定式的影响,应从多角度去思考、分析问题,必要的情况下通过反例的构造,能让冗长的问题变得短小、精炼.
2 反例法在概念教学中的应用
高中数学概念比较抽象,有些学生在学习概念时不得法,凭借死记硬背来掌握概念,因对概念的内涵缺乏深刻理解,而导致在概念的表达或应用时错误百出.倘若在概念形成的教学阶段,能让学生从深层次剖析概念的内涵,辨析常见错误产生的原因,则能帮助学生从反面或侧面挖掘出概念的本质,建构完整的认知.将反例法应用到概念教学中,对一些基础薄弱的学生而言,能改变他们所存在的概念模糊或认识不完整的状况.
比如,对韦达定理的认识,学生的思维受原有认知经验的束缚,常认为两根之和为一次项系数的相反数,两根的积为常数项.妥妥地忽略了定理中一个很重要的条件:平方项的系数未必是1.
这是一个可以避免的错误,教师在教学时,可向学生提出:ax2+bx=c=0两根的和是-b,积为c,这种说法对吗?
若学生认为这种说法是错误的,教师就趁机追问,错在哪儿?
通过反例的构造,不仅能弥补学生思维中对韦达定理认识不全的问题,还能让学生对概念学习产生新的认识,为后期的学习奠定基础.
3 反例法在错题教学中的应用
教学中,不少学生受惯性思维的影响,解题时会想当然地按照自己的意愿给出相应的结论.为了避免思维定式带来的副作用,教师可引导学生在适当的时候应用反例,激发学生的认知冲突,通过矛盾的解决来获得问题的本质.
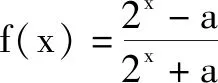
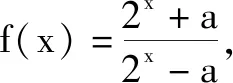
不论f(0)=0还是f(-x)=-f(x)的计算,这些错误发生的关键性因素,还是因为学生对于奇函数的定义没有达到深刻理解的程度,对f(0)=0的适用范围没有产生足够的认识.为了让学生找到错误产生的根源,避免此类问题的再次发生,笔者构造了反例问题,达到帮助学生纠错,提升思维的作用.
问题(1)a=1是怎么得到的?(根据f(0)=0得来.)
(2)是不是奇函数就一定有f(0)=0?(f(x)是奇函数时,f(-x)=-f(x)⟹f(-x)+f(x)=0,f(0)=0.)

(4)回顾第(2)个问题,来分析另一个学生的答案.(函数f(x)定义域为D,如果0∈D,根据f(0)=0可以得到a=1;如果0∉D,根据20+a=0⟹a=-1;也可以利用特殊值f(1)+f(-1)=0⟹a=±1.)
通过以上环环相扣的问题,容易发现,函数f(x)定义域为D,如果0∈D,就一定存在f(0)=0;而0∉D,f(x)为奇函数时,就一定存在20+a=0,a=-1.
随着设问、追问,以及反例的应用,学生经历了探究错误根源的过程,并在不断的思考、分析与推理中更进一步理解问题的本质.
正例与反例是相互对立又统一的关系,教学中若想单纯地凭借正例解决一切问题,这是不现实的.很多时候,反例能衬托出知识的核心,让不易发现的错误暴露于学生的思维中.因此,笔者常将反例法应用到错题教学中,以激活学生的思维,帮助学生提炼知识,达到融会贯通的目的.
4 反例法在特殊情况中的应用
特殊与一般是相互对立又相互依赖的关系,有些问题可把它们的特殊情形作为突破口,从独特的性质或变化规律中,找出解题途径,实现从特殊中发现一般的规律,又用特殊来否定一般的目的.因此,将反例应用于特殊情况中,是实现问题突破的重要方法之一.
例3判断正误:如果函数f(x)与其反函数f-1(x)的图象存在交点,那么此交点一定在直线y=x上.
面对此题,若从正面去判断比较麻烦,而反例的应用,则能使判断过程变得清晰,简洁.本题若用“函数y=-x”作为反例,即可判断,问题也就得以解决.但不少学生遇到此题时,并不能一下子就想到用反例法,这就需要教师在日常教学中多加引导,让学生有更多机会接触到类似的问题.如此,对培养学生的创新意识与逆向思维具有深远的影响.
其实,反例教学法除了应用于以上几种情况,还有更多、更广泛的应用范围,在此就不一一举例说明,但它对数学教学的重要影响有目共睹.教学中,教师应引导学生在恰当的时候,灵活应用反例,以增强学生对知识的理解,提高解题能力的同时形成良好的数学思想.
总之,反例教学法对数学概念、定义、解题等教学具有重要影响.它能提高学生对谬误的识别能力,锤炼学生的数学思维,为抽象逻辑思维与逆向思维的发展奠定基础,还能帮助学生形成辩证统一的思维品质,为学生的可持续性发展与数学核心素养的形成夯实基础.

