一题多解 提升数学创新思维能力
——以“立体几何二面角的多种解法”为例
江苏省苏州市相城区陆慕高级中学
吴 静
二面角的解法是立体几何的一个重要内容,它能有效地培养学生的空间想象、几何直观、逻辑推理、运算求解等能力.教师如果能引导学生一题多解,更能充分提升他们思维的广阔性、深刻性、探索性、灵活性、独创性等,进而促进创新思维的形成.
1 “一题一解”不能适应学生素养发展的需求
学生处理二面角的计算问题主要有两个方法:一是通过作出二面角的平面角,再在三角形中使用余弦定理.另外一个是向量法,即通过建立空间直角坐标系,计算出两个平面的法向量的夹角.但是在平常的数学训练中,学生遇到具体的问题时,往往只能想到其中一种方法,当这种方法出现卡壳时,解题就会出现困难.比如,学生会遇到作不出二面角的平面角或图形不规则不能够顺利建系等情况.
例1如图1所示,在三棱柱ABC-A1B1C1中,点E,F分别在棱BB1,CC1上(均异于端点),AB=AC,∠ABE=∠ACF,BB1⊥平面AEF.

图1
(1)求证:四边形BEFC是矩形;
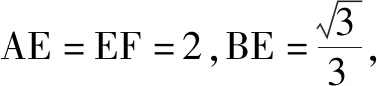
教师可以先问学生例1考查的知识点是什么.显然例1以斜三棱柱为载体,考查线面的位置关系以及二面角的计算.对于第(1)问,学生通过证△ABE≌△ACF得到BE=CF.又从BE∥CF,BE⊥EF出发,进而证得四边形BEFC是矩形.班上中游以上的学生基本能做出来.对于第(2)问,可以转化为求平面ABC与平面AEF所成的锐二面角,但是学生却发现这两个平面没有现成的交线,因而不好直接作出二面角的平面角.这道题目的难点就在于图形不常规,学生不知道如何建系.要让学生突破“一题一解”的羁绊,即突破一种类型的题目一种解法的瓶颈,教师就需要培养学生的创新思维.
2 “一题多解”提升创新思维能力的策略
教师可以结合二面角的解法,基于变式教学理论,以例1为例,以“一题多解”为展示的主要方式,最终促成学生创新能力的生长.
2.1 直接建系法
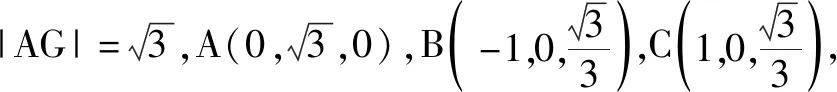
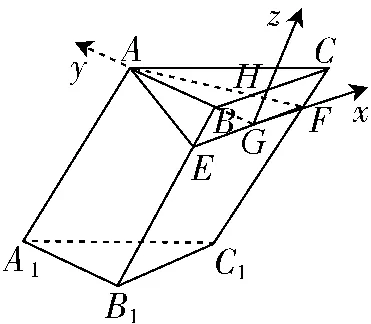
图2
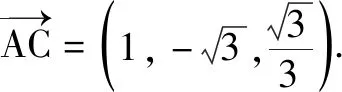
2.2 补交作角法
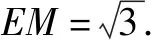
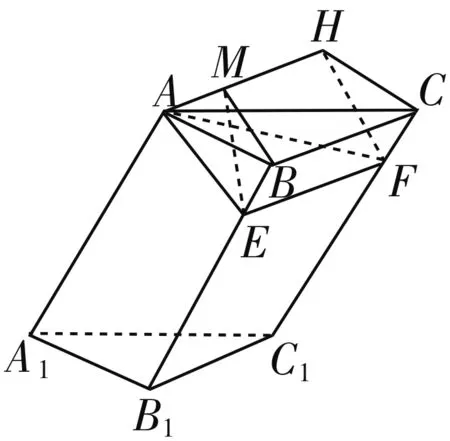
图3
这种解法的创新在于,通过延展两个平面找到两个半平面交线,在一个平面内向交线作一条垂线再证一个垂直(三垂线定理)得到二面角的平面角.学生只需要在直角三角形中通过勾股定理计算各边,进而直接得到余弦值.
2.3 平行平面法
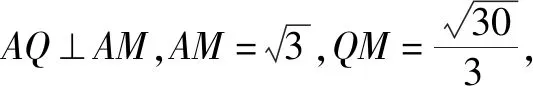
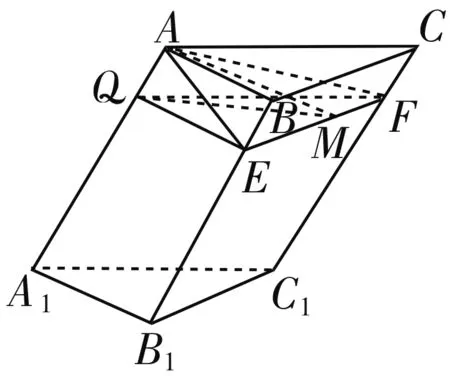
图4
这种解法的创新在于,学生通过作出一个平面的平行平面,将问题转化到两个有交线的平面上,学生可以直观地作出二面角的平面角,但教师要提醒他们有时候转化后的平行平面所成的二面角与原二面角是补角关系.
2.4 抽象作角法
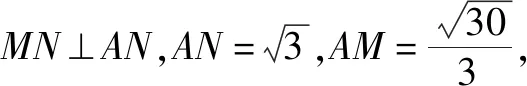

图5
这种解法的创新之处有反其道而行之的意蕴,教师不是指导学生找两个平面的交线,而是从交线上的一个点出发,在两个平面内分别作交线平行线的垂线作出二面角,表面上貌似不按图“索骥”,实则真正抓住了二面角平面角的本质.一言以蔽之,立体几何作为高中数学的主干知识之一,教师可借助“一题多解”将几何体的形状、大小与位置关系等,通过二面角的解法呈现出来.学生在解题的过程中将空间点、直线、平面的位置关系,空间向量与空间角的计算等串联起来.创新能力盘活了学生的认知,激发了他们的思维,进而促进了他们多元能力的生长.
高中数学课堂要以学生为本,教师要注重学生能力发生的过程.“一题多解”将教学的关注点转移到学生身上,不再是“一题多讲”,而是要凸显学生在思维上的“多”,即多创新思维;同时也凸显学生在展示上的”多“,即多创新展示.这样,学生的创新能力在具体的教学环节中才能得到长足的发展.
——四川美术学院雕塑系建系70周年文献展在重庆开幕

