基于往返式平漂探空的FY-3D卫星反演温度检验
周雪松 郭启云 夏元彩 田 泓
1)(内蒙古自治区呼和浩特市气象局,呼和浩特 010020)
2)(中国气象局气象探测中心,北京 100081)
引 言
目前世界各国进行高空气象探测的手段包括气球探空、卫星、飞机、雷达等[1],探测数据的准确性是数据应用的基础[2]。卫星作为重要的大气探测设备,发射升空后需对其上的仪器载荷进行定标和检验评估[3]。气球探空观测在当代气象观测中具有极其重要的地位[4],因其受地形、地物及人类活动影响较小,可定时定点对高空大气进行观测[5]。气球探测可获得大气温度、气压、湿度、风等要素的直接观测数据[6],数据准确度相对较高[7],可作为地基遥感观测、卫星遥感观测等的比对参考标准[8-10]。探空数据能够反映强对流天气发生前大气的温湿结构及动力特征[11],是分析局地强对流天气的重要数据之一,预报员常使用对流参数进行潜势预报[12]。目前,常规气球探空观测业务施放时间为每日07:15(北京时,下同)和19:15,获得的探测廓线间隔为12 h。强对流天气持续时间短、空间尺度小[13],常规探空观测对强对流天气过程预报预警的能力偏弱。往返式平漂探空观测是中国气象局研发的一种新型探空观测技术,该技术通过1 次施放,实现上升-平漂-下降3段观测[14],可实现间隔约6 h 的两次对流层垂直探测(上升段和下降段)和持续4 h 平流层高度的持续水平探测[15]。平漂探空采用导航卫星定位,技术更先进、数据更稳定[16]。经评估,平漂探空探测精度达到世界气象组织(World Meteorological Organization,WMO)规定的突破目标[17]。本文主要介绍利用平漂探空数据对卫星温度廓线和平流层大气温度数据的检验评估。
1 数据与方法
1.1 数据简介
1.1.1 探空数据
探空数据是探空仪跟随探空气球升空直接测量的大气状态数据,是目前准确度相对较高的大气探测数据,可作为卫星反演大气温湿度廓线的评估基准[18-19]。探空仪探测的数据包括时间、经度、纬度、海拔高度、温度、湿度和气压[20-21]。本文采用长江中下游的安庆、武汉、南昌、赣州、长沙、宜昌6个探空站的平漂探空数据。本次平漂探空观测于2021年3月开始,首次在国内开展了长达7个月的连续观测,施放时间为每日07:30和19:30(为保证业务探空顺利进行,平漂探空观测试验施放时间延后15 min)。经统计,平漂时段平均高度为28.489 km,主要集中在平流层中下层。
1.1.2 卫星数据
FY-3D 卫星是我国第2代极轨气象卫星[22],其装载的微波温度计、微波湿度计等设备可为数值预报、灾害性天气监测、气候变化研究提供有力数据支撑[23-24]。卫星轨道高度830 km,每日绕地14圈完成对全球的完整探测。卫星每完成1圈探测生成1个HDF格式数据文件(HDF 格式是一种具有自我描述性、可扩展性、自我组织性的广泛应用于科学研究领域的数据存储格式)[25-26]。卫星数据采用L2级产品中的大气温湿度廓线(AVP),垂直方向包含43个规定气压层,数据内容包括1212条扫描线的时间(日和毫秒计数数据)及每条扫描线90个像元数据的地理经纬度、海陆掩码、高程、太阳天顶角/方位角、卫星天顶角/方位角等数据,以及每个微波温度计(MWTS)视场的MWTS亮温、匹配微波湿度计(MWHS)亮温、云量(融合自成像仪)、微波湿度计反演的洋面降水检测结果、大气温湿廓线、由数值预报场插值至MWTS视场的大气温湿度廓线等数据。
1.2 时空匹配
气象观测数据具有代表性、准确性、可比较性,不同仪器的观测数据在一定的时间和空间范围内才具有可比性。因此,利用平漂探空数据对卫星数据检验,需设定时间和空间匹配条件。黄艺伟等[27]利用L波段探空数据对FY-4A 卫星温度廓线进行检验评估,其时间匹配利用探空气球施放和爆炸时间筛选时间段内的卫星数据。空间匹配则根据探空气球漂移的经纬度,以探空气球漂移轨迹的中点和漂移最远点的距离为半径画圆,采用最邻近法筛选卫星数据。本文时空匹配算法基于卫星数据和平漂探空数据的经纬差和时间差匹配,时间匹配条件为3 h,距离匹配条件为300 km。
时间匹配以卫星时间为基准,按照时间匹配条件,卫星数据与平漂探空数据时间差小于3 h。通过卫星和平漂探空数据文件中观测起止时间,筛选符合时间匹配的数据文件。对卫星数据检验时还需要对每组匹配数据进行时间匹配检查,确保检验评估的准确性。平漂探空数据的时间为北京时,卫星数据时间为世界时,本研究将时间统一转换为北京时。
空间匹配保证对比分析的一组卫星和平漂探空数据间的距离小于300 km。由于卫星数据覆盖范围远大于平漂探空的轨迹范围,为简化计算,可先确定平漂探空3段数据中每段的经纬度范围,据此确定矩形区域,将该区域向外扩展300 km,即可获得符合空间匹配的全部卫星数据。假设两点的经纬度分别为(H,J)和(K,L),则两点之间的距离

式(1)中,E=sinL·sinJ·cos(K-H)+cosI·cosJ,R是地球半径,为6371.39 km,π为圆周率。
1.3 数据处理
本文卫星数据气压范围为0.1~1013.25 h Pa,包含43个规定气压层。平漂探空数据由其状态时间信息分为3段分别处理:施放时间与外球炸时间(外球炸时间是指平漂探空观测外球爆炸的时间)确定上升段数据的起止索引;平漂开始时间与下降开始时间确定平漂段数据的起止索引;下降开始时间与终止时间确定下降段数据起止索引。
1.3.1 廓线数据处理方法
平漂探空上升和下降段为廓线数据,数据处理方法相同。根据卫星43个规定气压层将上升段、下降段数据稀疏化处理为与卫星数据垂直分辨率相同的廓线数据。上升段、下降段数据从地面至高空10 h Pa左右,探空仪升速约400 m·min-1,每秒发送1次数据,具有较高垂直分辨率,垂直层次可达数千层[28],因此,利用线性插值(式(2))计算温度误差也相对较小,可满足卫星数据检验要求:

式(2)中,T和P为插值点的温度和气压,T0和P0为下层的温度和气压,T1和P1为上层的温度和气压。
根据平漂探空上升、下降段廓线轨迹提取卫星廓线数据,具体步骤:①根据平漂探空廓线的气压值范围,筛选其包含的卫星规定气压层次。②获取探空廓线中规定气压层次(与卫星对应)的数据时间、温度、湿度、经度、纬度。③利用数据经纬度、数据质量标志、数据时间,从卫星数据的各规定气压层中筛选与探空轨迹距离最近且满足时空匹配条件的数据,即完成卫星廓线提取。
1.3.2 平漂段数据处理方法
平漂探空的平漂段数据是高时间分辨率、长持续时间的平流层观测,其平漂距离可达300~500 km,可用于卫星平流层反演温度的检验评估,数据处理方法如下:
①确定卫星数据的经纬度。首先确定探空平漂段轨迹的经度和纬度范围,筛选卫星数据。由于卫星数据的范围远大于平漂探空的轨迹范围,平漂探空数据通常被包含在卫星数据的经纬度范围内。为避免数据遗漏,将平漂段的经纬度范围向外扩展300 km(最大匹配距离),此范围内的卫星数据即为符合空间匹配条件的数据集合。将范围内的卫星数据与平漂段数据进行时间和空间匹配,由于平漂段的数据分辨率较高,每个卫星数据点将获得多个符合空间匹配条件的平漂探空数据点,选取距离最近的数据点作为检验数据。
②确定卫星数据的规定气压层次。卫星温度数据的空间定位信息为三维数组,确定其经度、纬度后,由平漂探空数据的气压确定卫星数据的气压层。平漂段的理想高度约为25 km,但气球平漂高度受天气、大气运动、净举力等因素影响,平漂高度存在微小浮动。平漂气压通常为10~30 hPa,跨越3~4个卫星规定气压层(10.37 hPa,14.81 hPa,20.4 hPa和27.26 hPa),每两个气压层间的垂直高度差约为2 km。同一时次的平漂段,其探测高度(气压)也非定值。利用平漂探空上升段廓线,统计10~30 h Pa间4个规定气压层附近的温度变化趋势发现:当平漂探空气压与卫星规定气压的差值小于临近规定气压值的百分之一时,平漂数据点与卫星规定气压处的温度差值较小,可直接采用该气压处的温度作为平漂高度的卫星温度数据;当平漂气压与规定气压的差值大于规定气压值的百分之一时,可利用卫星上下规定层的温度和气压,通过插值算法计得到该平漂高度的卫星温度数据,且误差较小。气压温度插值公式如下:
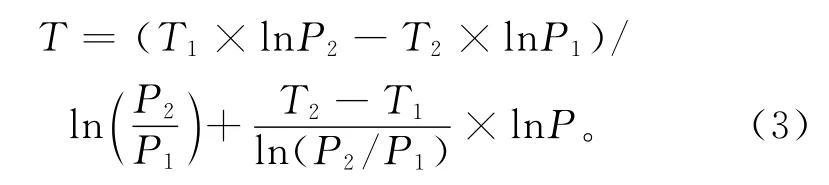
整理式(3),得到
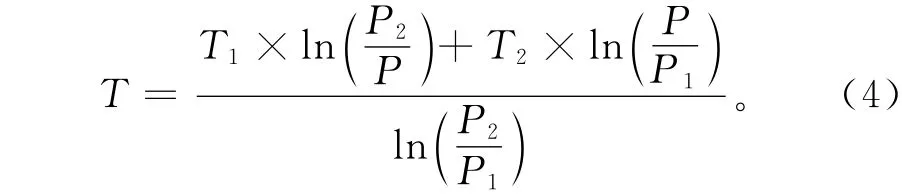
式(4)中,P1和P2为两规定气压层,T1和T2为两规定层处的温度,P为插值点气压,T为插值点温度[29]。利用2021年3—9月长江中下游试验上升段温度数据验证气压温度插值算法,结果显示:在10.37~14.81 hPa,14.81~20.4 hPa,20.4~27.26 hPa规定气压层内,误差集中在±2℃内,4个规定气压层间的平均绝对偏差分别为0.70,0.65℃和0.56℃,误差相对较小。因此,上述方法满足卫星平流层温度的检验评估需求。
2 检验结果
选取2021年3—9月长江中下游6个站点的平漂探空试验数据,以及该时间段中国区域FY-3D 卫星数据,其中平漂探空数据文件共2798份,卫星数据文件1110份。文中将平漂探空数据分为上升段、平漂段和下降段分别统计,统计结果如表1 所示。由表1可知,卫星温度廓线与平漂探空上升段温度平均相关系数为0.99(达到0.01显著性水平),平均绝对偏差为1.34℃,平均均方根误差为1.95℃。与下降段温度平均相关系数为0.99(达到0.01显著性水平),平均绝对偏差为1.93℃,平均均方根误差为2.46℃。上升段与下降段的平均绝对偏差小于2℃,平均均方根误差为2~2.5℃,相关系数接近1。由检验结果数据可知,对流层内卫星反演温度廓线数据准确度较高。卫星平流层温度与平漂段相关系数仅为0.04(相关不显著),平均绝对偏差和平均均方根误差分别为3.92℃和4.10℃,比对流层内卫星反演温度廓线的误差略大。由于平漂段数据观测持续时间较长,平漂距离较远且方向随机,最优时间匹配和最优空间匹配二者不可兼得。本文采用距离优先的匹配算法,即从时间差小于3 h的数据中筛选距离卫星数据点最近的平漂段数据点作为检验数据。再者,匹配条件是通过时间差和距离差筛选数据,差值不区分正负,因此平漂段的检验结果相关性较差。

表1 卫星数据检验评估结果Table 1 Inspection and evaluation of satellite data
2.1 利用上升段数据的检验评估
上升段数据是由6 个探空站每日07:30 和19:30 施放探空仪至外球爆炸的探空观测获得,共完成367次匹配,平均每站61次,各站检验结果如表2所示。
2.1.1 07:30上升段检验
07:30平漂探空上升段观测数据代表清晨时刻的温度廓线,清晨太阳初升,地面升温较快,数据时差对检验结果影响较大,尤其是近地面至850 hPa[30]。由于卫星数据与探空数据时间差小于3 h,较多匹配数据时差大于1 h,造成近地面检验结果误差偏大。图1是2021年4月11日07:30南昌站上升段探空数据对卫星温度廓线检验。由图1可知,卫星廓线与平漂探空上升段温度数据趋势基本一致(图1a),800 h Pa 以上误差较小(图1c和图1d),但受日出辐射和局地地形因素影响,近地面温度误差略大,最大超过-3.5℃(图1b和图1c),平漂探空温度数据与卫星温度数据误差主要集中在-2.0~2.0℃(图1d)。由表2 各站07:30检验结果可知,除长沙站平均绝对偏差为2.15℃,均方根误差达到2.95℃外,其余各站偏差均为1.12~1.51℃,均方根误差为1.48~1.99℃。各站平均绝对偏差为1.44℃,平均均方根误差为1.94℃。因此,07:30卫星温度廓线数据的总体准确度较高。
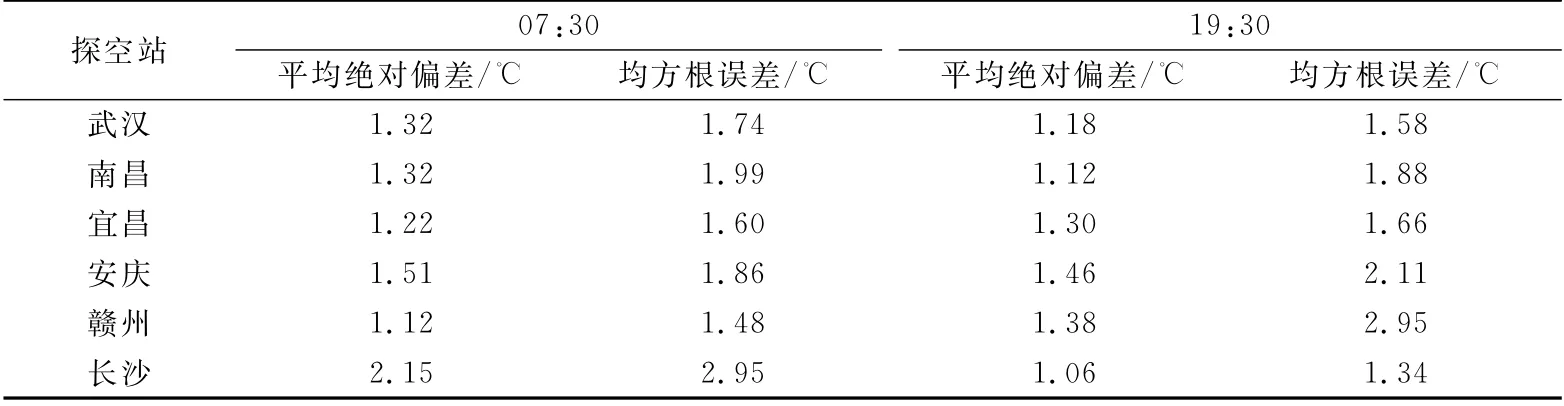
表2 上升段卫星数据检验评估结果Table 2 Inspection and evaluation of satellite data at ascending section
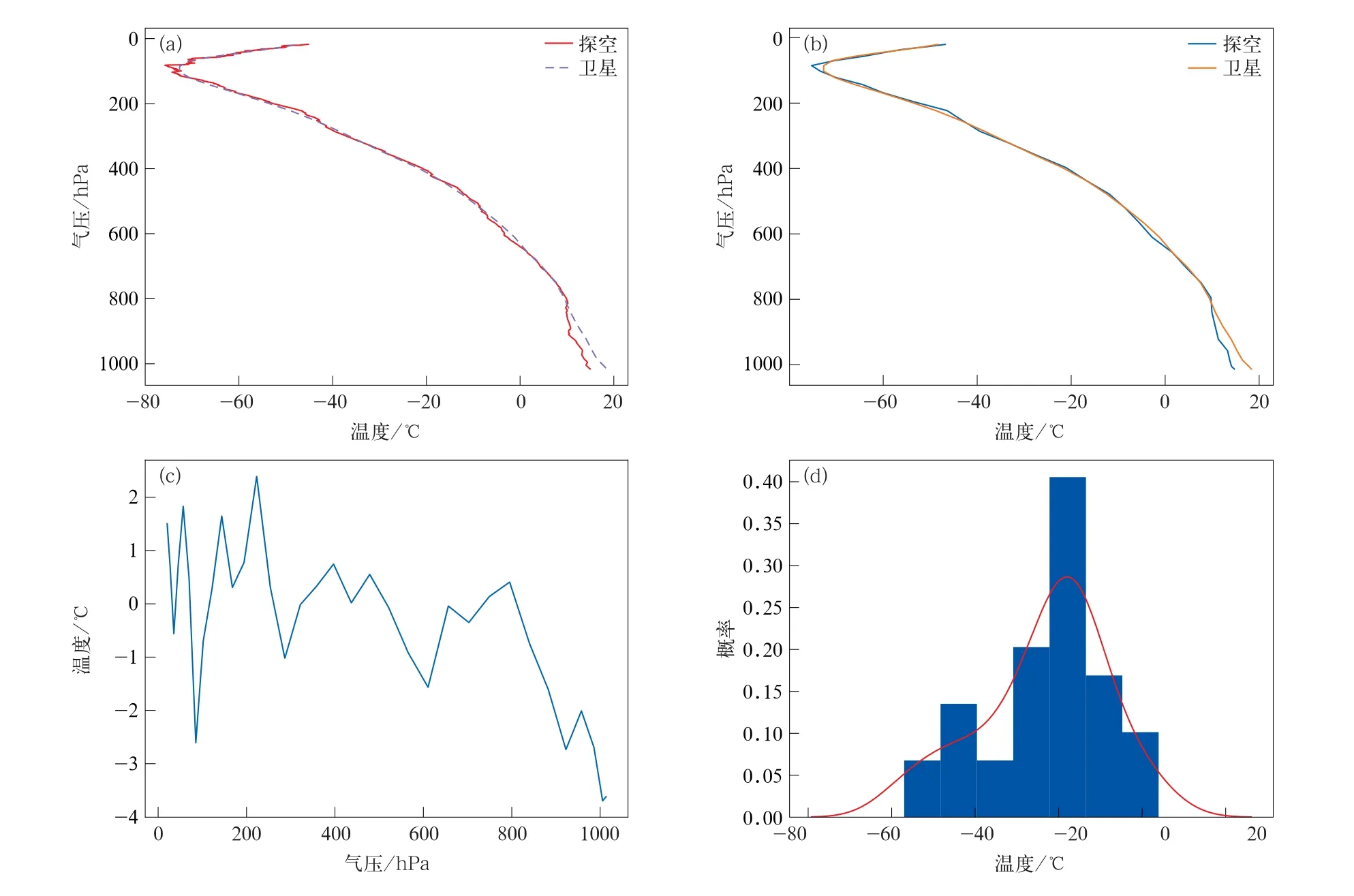
图1 2021年4月11日07:30南昌站上升段(a)卫星与原始探空温度廓线,(b)卫星与稀疏化探空温度廓线,(c)温度误差随气压变化,(d)温度廓线误差分布(红色曲线为拟合线)Fig.1 Ascending section of Nanchang Station at 0730 BT 11 Apr 2021(a)temperature profiles from satellite and original sounding,(b)temperature profiles from satellite and sparse sounding,(c)temperature error varying with air pressure,(d)error distribution of temperature profile(red curve denotes fitting curve)
2.1.2 19:30上升段检验
19:30平漂探空上升段温度廓线代表傍晚时刻的温度廓线数据。图2是2021 年4 月5日19:30赣州站上升段探空数据对卫星温度廓线数据的检验评估。由图2可知,19:30的卫星数据与探空温度廓线一致性较好(图2a和图2b),仅在100 h Pa高度以上和850 hPa附近误差偏大(图2c),卫星数据与探空数据温度误差较小,总体误差集中在±1℃(图2d)。由表2 可知,各站19:30 数据的平均绝对偏差、平均均方根误差较小,分别为1.25℃和1.92℃。与07:30上升段数据的检验结果相比,19:30上升段各站数据检验误差更小。
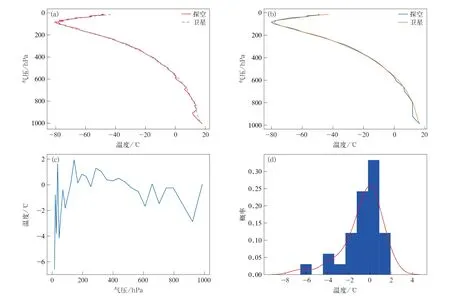
图2 2021年4月5日19:30赣州站上升段(a)卫星与原始探空温度廓线,(b)卫星与稀疏化探空温度廓线,(c)温度误差随气压变化曲线,(d)温度廓线误差分布(红色曲线为拟合线)Fig.2 Ascending section of Ganzhou Station at 1930 BT 5 Apr 2021(a)temperature profiles from satellite and original sounding,(b)temperature profiles from satellite and sparse sounding,(c)temperature error varying with air pressure,(d)error distribution of temperature profile(red curve denotes fitting curve)
2.2 利用平漂段数据的检验评估
由于日间平漂段探测数据的太阳辐射订正尚未完成,卫星平流层大气温度检验仅选取19:30施放的夜间平漂段探测数据。19:30平漂段为平流层的夜间持续观测,气球升空后距离放球点较远,且无太阳辐射影响,各探空站数据差异主要由平漂轨迹和高度决定。图3是2021年6月11日19:30长沙站平漂段数据对卫星平流层反演温度的检验评估。由图3可知,平漂探空温度与卫星反演温度趋势基本一致,但卫星反演温度比平漂探空观测温度值偏高且误差符号一致(图3b和图3c)。平漂探空数据波动明显,更真实地展示大气温度的变化情况,而卫星反演的温度数据受分辨率限制,曲线相对平滑,无法反映平流层大气温度的细微变化(图3a和图3b)。卫星平流层反演温度误差多为-4~-1℃(图3c和图3d),与温度廓线相比,误差偏大。

图3 2021年6月11日19:30长沙站平漂段(a)卫星与原始探空温度廓线,(b)卫星与稀疏化探空温度廓线,(c)温度误差随时间变化曲线,(d)温度廓线误差分布(红色曲线为拟合线)Fig.3 The horizontal drift section of Changsha Station at 1930 BT 11 June 2021(a)satellite and original sounding temperature profile,(b)satellite and sparse sounding temperature profile,(c)curve of temperature error changing with time,(d)error distribution of temperature profile(red curve denotes fitting curve)
19:30平漂段与卫星数据匹配249次,各站统计结果如表3所示。由表3可知,卫星平流层反演温度的检验结果比温度廓线略差,各探空站温度平均绝对偏差为3.93℃,平均均方根误差为4.10℃。南昌站的检验结果最优,温度平均绝对偏差为3.03℃,均方根误差为3.20℃;武汉站、宜昌站、赣州站次之,温度平均绝对偏差为3.24~3.56℃,均方根误差为3.41~3.72℃;长沙站的数据偏差最大,温度平均绝对偏差达5.97℃,均方根误差为6.09℃。由于平漂段气球飞行的高度非定值,探测高度难以准确控制在卫星规定气压高度,检验评估时需将卫星规定气压层的温度插值至平漂探测高度,插值算法误差为-2~2℃,造成卫星平流层反演温度的检验结果存在一定误差。
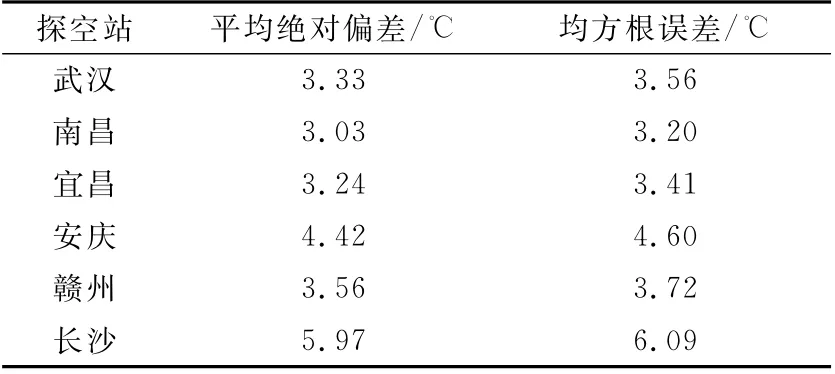
表3 平漂段卫星数据检验评估结果Table 3 Inspection and evaluation of satellite data at horizontal drift section
2.3 利用下降段数据检验评估
下降段数据为平漂结束、探空仪随降落伞下落的观测数据,与上升段时间间隔约为6 h。下降段共匹配769次,受平漂距离和接收机布设密度影响,下降段数据质量、终止气压因站而异。下降段数据的检验结果如表4所示。
2.3.1 13:30下降段检验
07:30平漂探空下降段数据为13:30廓线,代表探测气球下落点午后的廓线数据。图4是2021年6月25日13:30武汉站下降段探空数据对卫星温度廓线检验评估。由图4可知,下降终止气压约为660 hPa,下降段整体温度曲线趋势一致,下降段探空数据总体比卫星温度廓线数值偏高(图4a和图4b)。温度数据误差多为0~2℃,但100 hPa以上误差明显偏大,(图4c和图4d)。由表4中13:30 检验结果可知,平均绝对偏差和均方根误差因站而异,其中武汉站、长沙站的平均绝对偏差分别为3.67℃和3.26℃,均方根误差分别为4.43℃和3.79℃,其余各站平均绝对偏差均在1.5℃左右,均方根误差约为2.0℃。6个探空站的平均绝对偏差、均方根误差的平均值分别为2.18℃和2.69℃。因此,13:30卫星廓线数据质量相对较高,明显优于平流层温度探测结果,但相较于上升段的检验评估结果,误差略大。
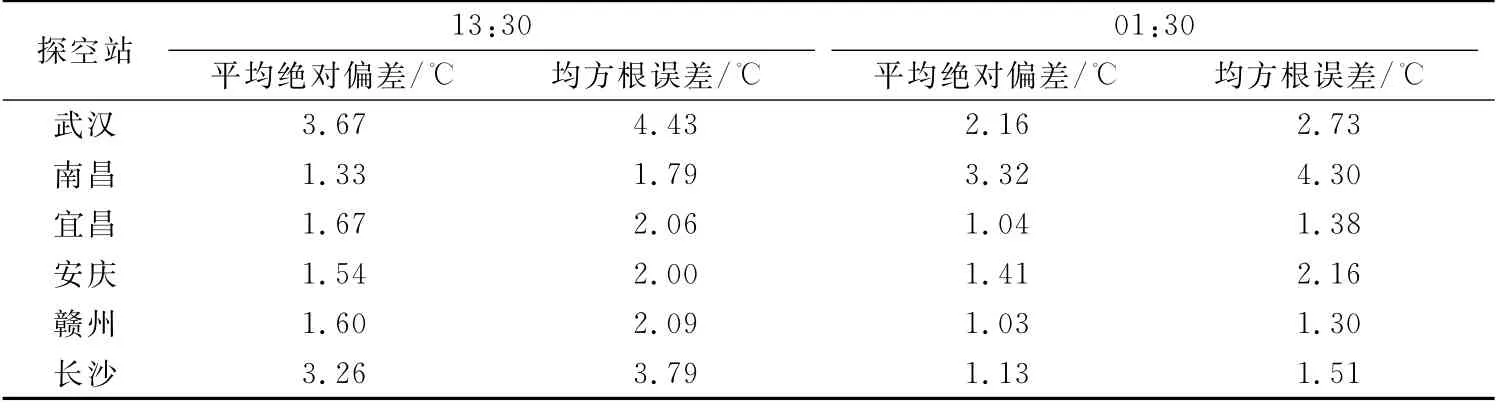
表4 下降段卫星数据检验评估结果Table 4 Inspection and evaluation of satellite data at descending section
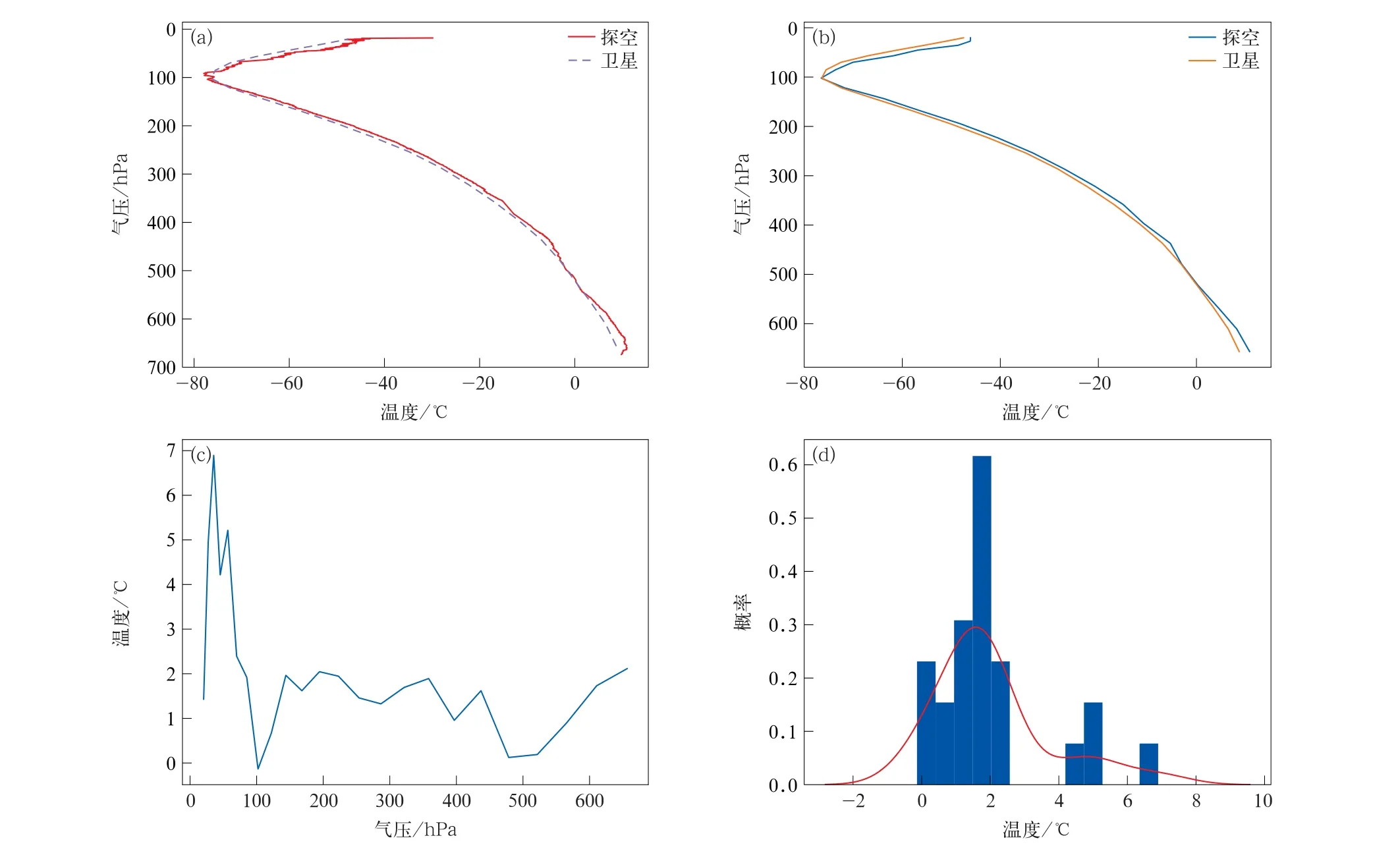
图4 2021年6月25日13:30武汉站下降段(a)卫星与原始探空温度廓线,(b)卫星与稀疏化探空温度廓线,(c)温度误差随气压变化曲线,(d)温度廓线误差分布(红色曲线为拟合线)Fig.4 Descending section of Wuhan Station at 1330 BT 25 Jun 2021(a)temperature profiles from satellite and original sounding,(b)temperature profiles from satellite and sparse sounding,(c)temperature error varying with air pressure,(d)error distribution of temperature profile(red curve denotes fitting curve)
2.3.2 01:30下降段检验
19:30平漂探空的下降段数据为次日01:30廓线,代表探测气球下落点夜间的温度廓线数据。图5是2021年4月9日01:30 宜昌站下降段探空数据对卫星温度廓线的检验评估。由图5可知,下降段整体温度曲线趋势一致,但探空温度廓线展示更多温度变化细节,而卫星廓线相对平滑(图5a和图5b)。卫星廓线检验误差多为-2~2℃以内,在50~200 hPa高度,误差略大(图5c和图5d)。由表4 01:30检验结果可知,01:30卫星温度廓线与探空温度廓线平均绝对偏差和均方根误差总体较小,其中武汉站、南昌站平均绝对偏差为2.16℃和3.32℃,均方根误差为2.73℃和4.30℃,其余各站平均绝对偏差为1.0~1.4℃,均方根误差为1.30~2.16℃。由于夜间无太阳辐射影响,近地面温度随时间变化较小,与13:30 的卫星温度廓线检验结果相比,01:30 卫星廓线检验结果相对较好。

图5 2021年4月9日01:30宜昌站下降段(a)卫星与原始探空温度廓线,(b)卫星与稀疏化探空温度廓线,(c)温度误差随气压变化曲线,(d)温度廓线误差分布(红色曲线为拟合线)Fig.5 Descending section of Yichang Station at 0130 BT 9 Apr 2021(a)temperature profiles from satellite and original sounding,(b)temperature profiles from satellite and sparse sounding,(c)temperature error varying with air pressure,(d)error distribution of temperature profile(red curve denotes fitting curve)
2.4 下降段检验评估误差
由表1可知,与上升段相比,下降段数据的检验评估结果误差偏大。其中平均绝对偏差偏大0.59℃,平均均方根误差偏大0.51℃,存在明显的系统性误差。目前,利用气球携带探空仪的上升段探空观测技术成熟、数据质量稳定,已经在试验和业务中得到充分验证。因此,下降段的误差来源需进一步讨论。
影响探空仪温度探测精度的因子很多,如升速/降速、传感器元器件的滞后性、天气系统、辐射订正等。上升段和下降段主要区别在于升速和降速的大小,经统计,上升段平均升速为340.1 m·s-1,平均最大升速为502.6 m·s-1,平均最小升速为273.0 m·s-1;下降段平均降速为498.1 m·s-1,平均最大降速为871.6 m·s-1,平均最小降速为297.6 m·s-1。下降段速度明显大于上升段,平均速度为上升段的1.46倍,平均最大速度为上升段的1.73倍,平均最小速度差别较小。上升段的升速相对稳定,受垂直气流影响升速略有波动,基本维持在6~8 m·s-1。下降段受天气系统、降落伞等原因影响,较多时次探测记录中探空仪下降速度从外球炸至落地逐渐增大,最大可达30 m·s-1。因此,受空气摩擦、温度传感器滞后误差等因素影响,探空仪下降段温度探测数据误差偏大。与上升段相比,下降段温度平均绝对偏差和均方根误差均增大约0.5℃。
2.5 卫星廓线误差
由2.3节可知,卫星温度廓线数据准确度总体较高,但不同高度的反演结果略有不同(表5)。由表5 可知,850 hPa以下(含850 h Pa)和100 h Pa至10 hPa的平均绝对偏差比850 hPa至100 hPa(含100 hPa)分别偏大0.52℃和0.59℃,平均均方根误差分别偏大0.31℃和0.59℃。由于地面至850 h Pa清晨温度变化较快,3 h匹配时间对检验结果影响较大,因此,850 hPa以下的检验结果不理想,并非完全由卫星数据造成。为减小时间偏差对检验结果的影响,利用19:30 上升段廓线对850 hPa 以下的卫星数据进行检验,其平均绝对偏差为1.49℃,平均均方根误差为1.71℃。与850 hPa至100 h Pa的检验结果相比,平均绝对偏差偏大0.33℃,平均均方根误差偏大0.09℃。

表5 不同高度卫星数据的检验结果Table 5 Test of satellite data at different altitudes
2.6 云对卫星反演温度的影响分析
卫星作为重要的天基遥感设备,其反演的大气温度廓线受云系影响较大[31]。由于长江中下游各站的云观测数据有限,暂时无法开展云对卫星反演温度影响的分析。周毓荃等[32]探讨利用探空数据分析云的垂直特征的方法,并利用云雷达观测数据对该方法进行验证,因此可利用探空湿度廓线分析云对检验结果的影响。与此同时,FY-3D 卫星的温湿廓线数据也包含每个像元的云量信息,为云占天空的百分比[33],范围为0~100%。由于数据中云量为0 和100%的样本较少,因此本文将云量低于10%记为无云,90%以上记为有云。利用探空湿度廓线云判识算法和FY-3D 卫星成像仪云数据分析云对卫星反演的温度数据的影响,结果如表6所示。

表6 云对卫星反演温度的影响Table 6 Influence of statistical cloud on satellite inversion temperature
由表6可知,利用探空湿度廓线云判识算法,有云情况下,上升段温度的平均绝对偏差偏大0.32℃,平均均方根误差偏大1.31℃;下降段温度的平均绝对偏差偏大0.35℃,平均均方根误差偏大0.28℃。由此可见,受云系影响,卫星反演温度的平均绝对偏差增大0.3~0.4℃,云对上升段检验结果的均方根误差的影响大于下降段。由FY-3D 卫星成像仪云数据的统计结果(表6)可知,有云情况下,上升段温度的平均绝对偏差偏大0.3℃,平均均方根误差偏大1.0℃;下降段温度的平均绝对偏差和平均均方根误差均偏大0.5℃,这与探空湿度廓线数据云判识算法的结果区别不大。
以上两种方法的统计数据均存在计算误差,主要有以下原因:①文中FY-3D 卫星成像仪云数据仅包含云量的占比,不能完全确定卫星反演的温度数据是否受云影响,且不同类型云的高度、厚度不同,对卫星反演的温度数据影响也不同;②探空湿度廓线的云识别方法只能识别廓线是否经过云层,由于探空廓线的水平移动距离较远,因此与其匹配的卫星数据未必受云影响;③云的移动速度较快,匹配条件的3 h时差、300 km 距离差对分析结果有较大影响。
3 结 论
本文介绍利用平漂探空数据检验卫星数据的算法,并实现对卫星温度廓线和平流层反演温度的检验。经验证,算法可实现对卫星数据检验,主要结论如下:
1)FY-3D 卫星反演温度数据的准确度总体较高,与平漂探空上升段和下降段数据的平均绝对偏差分别为1.34℃和1.93℃,平均均方根误差分别为1.95℃和2.46℃。
2)由19:30的上升段探空廓线对卫星数据检验的结果可知,100 hPa以上和850 hPa以下(含850 h Pa)卫星反演温度的平均绝对偏差比850 hPa至100 hPa(含100 hPa)分别偏大0.59℃和0.33℃。
3)由于卫星温度数据在100 hPa以上误差偏大,卫星反演平流层的温度准确度低于温度廓线,平均绝对偏差约为3.92℃。
4)与平漂探空数据相比,卫星反演的大气温度分辨率较低、趋势较平滑,无法显示大气温度垂直分布和平流层温度水平分布的细节特征。由于卫星平流层温度检验利用上下两规定气压层温度通过插值计算平漂高度的温度,因此卫星平流层温度检验算法误差为-2~2℃。
5)由探空湿度廓线数据云判识算法可知,受大气中云的影响,卫星反演温度的平均绝对偏差增大0.3~0.4℃。
由于检验评估的数据存在较多匹配数据接近临界匹配条件,使检验结果存在一定误差,今后将利用时空匹配度更高的观测数据对卫星反演的温度数据进行检验评估。

