应用贝叶斯模型平均法建立东北云冷杉针阔混交林蓄积生长模型1)

贾勃 王新杰

(北京林业大学，北京，100083)

针阔混交林是一种典型的森林植被类型，在东北地区森林生态系统中具有不可替代的作用，准确预估针阔混交林蓄积量对森林经营具有现实意义。随着模型的愈加成熟，林业研究人员根据自变量和因变量的关系采用了多种模型方法进行预估蓄积量，参数回归方法大致分为线性方程和非线性方程，具有解释性强的优点；非参数回归方法(例如机器学习)简单易操作，但存在计算量大，对样本数要求高，易发生过拟合的缺点。洪奕丰等[1]、刘琼阁等[2]基于偏最小二乘法估测蓄积量；闵志强等[3]采用多元线性回归的方法对云南松的蓄积量进行估算；唐文静等[4]采用随机森林的方法估测森林蓄积量及其动态变化；周宇飞等[5]、曾霞辉[6]采用无人机影像数据估测森林蓄积量；王海宾等[7]和李世波等[8]基于高分一号遥感估测森林蓄积量；曾伟生等[9]、袁钰娜等[10]利用激光雷达数据估测森林蓄积量。

然而不断发展的这些蓄积量模型，仍无法很好地解决模型存在较大的不确定性的问题[11]。解决模型不确定性的方法主要是将模型误差归结为模型参数的不确定性，进而以观测数据为基准进行模型参数优化。但这种方法也忽略了模型结构的不确定性，因此，针对模型结构的不确定性，贝叶斯模型平均法(BMA)被众多研究者采纳应用，被认为可以解决模型的不确定性问题，较单一模型也能够提高模型模拟和预测的精度[12]。贝叶斯模型平均法是利用多模式集合进行概率预报的处理方法，它允许枚举和评估大量可能的模型，以清楚地表示它们与数据和参数的匹配程度。与典型的逐步回归方法相比，贝叶斯模型平均法降低了在变量选择上产生偏差的可能性。大量研究表明，贝叶斯模型平均法的预测结果比单一模型的结果更为可靠。贝叶斯模型平均法在医学[13]、水利[14]等方面得到了广泛应用。王慧亮等[15]运用贝叶斯模型平均法进行了河流污染点的模拟，巴欢欢等[16]、刘家琳等[17]、赫淑杰等[18]应用贝叶斯模型平均法对洪水发生的概率进行了预测；Lu et al.[19]利用贝叶斯模型平均法构建了杉木人工林树木死亡率与立地、竞争和气候因素的关系；白海峰等[20]运用贝叶斯模型平均法构建森林火灾预测模型，有效提高林火预测的精度；王震等[21]构建了福建杉木人工林林分蓄积量生长模型，模型表现优于逐步回归方法。

本文应用贝叶斯模型平均法针对东北云冷杉针阔混交林进行林分蓄积生长模拟，分析林分蓄积量与林分因子、气候因子的关系，以期为东北云冷杉针阔混交林的合理经营提供依据。

1 研究区概况

研究地点位于吉林省汪清林业局金沟岭林场，东经130°5′～130°20′，北纬43°17′～43°25′，属吉林省东部山区长白山系老爷岭山脉雪岭支脉(见图1)。地貌属于低山丘陵，海拔300～1 200 m，平均坡度10°～25°。该地区属温带大陆性季风气候，年均气温3.9 ℃。1月份气温最低，平均最低气温-32 ℃；7月份气温最高，平均最高气温32 ℃；全年无霜期达138 d；年降水量600～700 mm，降水多集中在7月。土壤类型主要为暗棕壤，土层平均厚度40 cm。主要树种有水曲柳(Fraxinusmandshurica)、鱼鳞云杉(Piceajezoensis)、枫桦(Betulacostata)、紫椴(Tiliaamurensis)、红松(Pinuskoraiensis)和色木槭(Acermono)等。

图1 调查样地位置示意

2 研究方法

2.1 数据来源

数据来源于2003、2008、2012、2017年对金沟岭林场固定样地部分调查数据，样地大小均为20 m×20 m。对样地内胸径大于5 cm的活立木进行每木检尺，记录树种名称、胸径、林分密度、坡向、坡度、海拔、土壤类型、坐标位置等信息。沿着坡的方向记录坡向，从坡上看坡下，表达方式为：以正北为0°，顺时针读度数，直到360°。经过选择符合要求的样地并剔除缺失数据的样地后，最终确定198块固定样地作为研究对象。

本文选择林分因子(林分平均胸径、林分断面积、林分密度)、地形因子(海拔、坡度、坡向)和气候因子作为构建模型的初始变量。

利用汪清地区一元材积表法[22]获得单木材积，汇总单木材积可得样地蓄积量，进一步推算出每公顷林分蓄积量(M)。样地林分因子和地形因子统计量见表1。

表1 林分因子统计表

气候变量是根据各样地经纬度坐标及海拔数据利用Climate AP软件[23]获得，本文获取的因子主要有年平均温度(MAT)、年均降雨量(MAP)、最暖月平均温度(MWMT)，最冷月平均温度(MCMT)、平均气温差(TD)、水分指数(AHM)、<0 ℃积温(DD_0)、>5 ℃积温(DD5)、<18 ℃积温(DD_18)、>18 ℃积温(DD18)、无霜期(NFED)、降雪量(PAS)、参考蒸发(EreF)、气候水分亏损(CMD)等，气候因子统计见表2。

表2 气候因子统计值

统计量>5℃积温/℃<18℃积温/℃>18℃积温/℃无霜期/d年降雪量/mm参考蒸发量/mm气候水分亏损/mm平均值1848.195363.47157.28171.7953.40701.78203.68标准差47.82215.4830.764.4519.2621.0571.29

2.2 模型构建

2.2.1 逐步回归(SR)

逐步回归是回归分析方法中常用的一种方法，运用逐步回归法进行建模，即选择一些线性关系较强的因子与因变量进行建模，从而得到较为理想的估测模型。逐步回归的一般表达式为：

Y=a0+a1x1+a2x2+a3x3+…+anxn+ε。

式中：Y为解释变量，a0为常数项，a1、a2、…、an为回归系数，x1、x2、…、xn为自变量，n为自变量个数。

逐步回归模型根据模型赤池信息量准则(AIC)值的变化及变量显著与否，剔除与因变量不显著的因子，最终确定模型形式。

2.2.2 贝叶斯模型平均法(BMA)

贝叶斯模型平均法(BMA)是由Rafery et al.[23]提出的一种利用多模型组合进行概率预报的统计方法，通过估算潜在变量(X)的所有可能组合的模型构建加权平均模型。在贝叶斯模型平均法中，模型的数量相当大，如果有n个自变量，模型个数为2n。贝叶斯模型平均法通过选择可能模型的子集，并使用这些模型的模型后验概率执行所有推断和预测。贝叶斯模型平均法指定先验分布，以模型后验概率(PMP)为权重对可能的单项模型进行加权平均，以解释变量的后验包含概率(PIP)的大小作为选择解释变量的客观标准。

一般认为，P<0.5表示该变量对因变量没有影响；0.50≤P<0.75表示该变量对因变量有弱的影响；0.75≤P<0.95表示该变量对因变量有较强的影响；P≥0.95表示该变量对因变量有极强的影响。

2.2.3 模型评价

本研究评价模型的拟合效果和预估精度采用决定系数(R2)和均方根误差(RMSE)。计算公式如下：

本研究选取数据的70%作为模拟数据，剩余的30%作为预测数据。分别使用逐步回归法和贝叶斯模型平均法构建林分蓄积量模型。所有的计算均在R软件中完成，利用step函数进行逐步回归，利用贝叶斯自适应抽样包BAS包实现贝叶斯模型平均法模型的构建[24]。在贝叶斯模型平均法的计算过程中，参数的先验分布采用Zellner-Siow柯西先验分布[25]。

3 结果与分析

3.1 变量选择

本文采用14种气候因子及7种林分因子进入模型拟合过程。贝叶斯模型平均法和逐步回归选择的变量如表3所示。采用逐步回归方法最终确定坡向、海拔、林分密度、林分断面积、林分平均胸径、最暖月平均温度、<0 ℃积温、<18 ℃积温、参考蒸发量等9个因子为模型影响因子，贝叶斯模型平均法(BMA)前5个模型选择的变量各不相同，以此建立与蓄积量的关系。

表3 模型选择

3.2 模型参数估计

逐步回归根据变量显著与否得出模型最佳形式，在一定程度上忽略了模型本身的不确定性。BMA模型考虑了所有可能的变量组合，考虑了林分蓄积量模型的不确定性。分别给出逐步回归和BMA法的参数估计值。

由表4、表5可知，在逐步回归方法中，林分蓄积量与坡位、林分断面积、平均胸径、最暖月平均温度、<18 ℃积温呈显著正相关关系，与海拔、林分密度、<0 ℃积温、参考蒸发呈显著负相关关系。在BMA方法中，林分蓄积量与林分密度呈极显著负相关关系(后验概率P>0.95)，与林分断面积呈极显著正相关关系(后验概率P>0.95),与海拔、<0 ℃积温、参考蒸发呈弱负相关关系(后验概率P<0.95)，与平均胸径、<18 ℃积温呈弱正相关关系(后验概率P<0.95)。

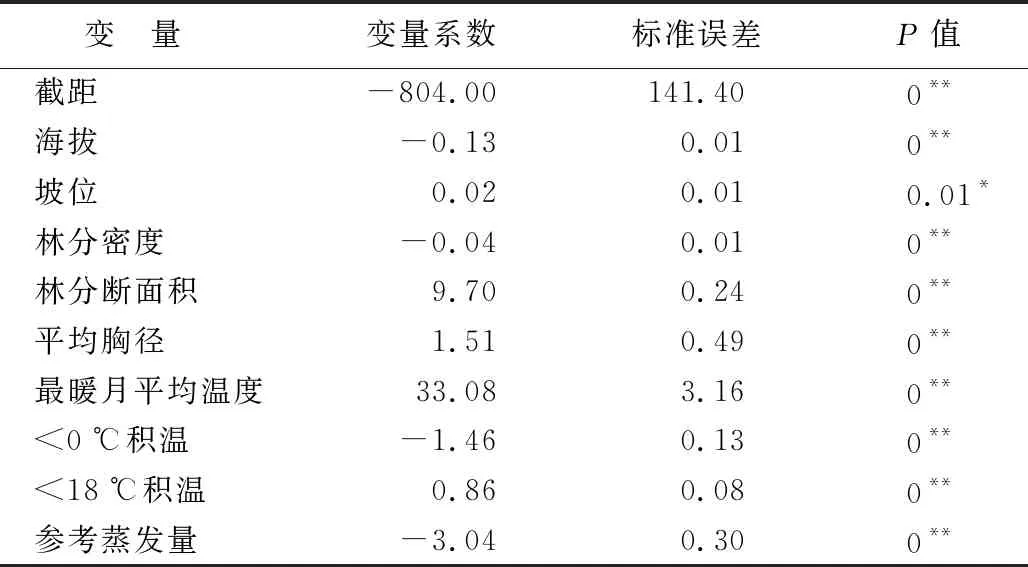
表4 逐步回归的参数估计

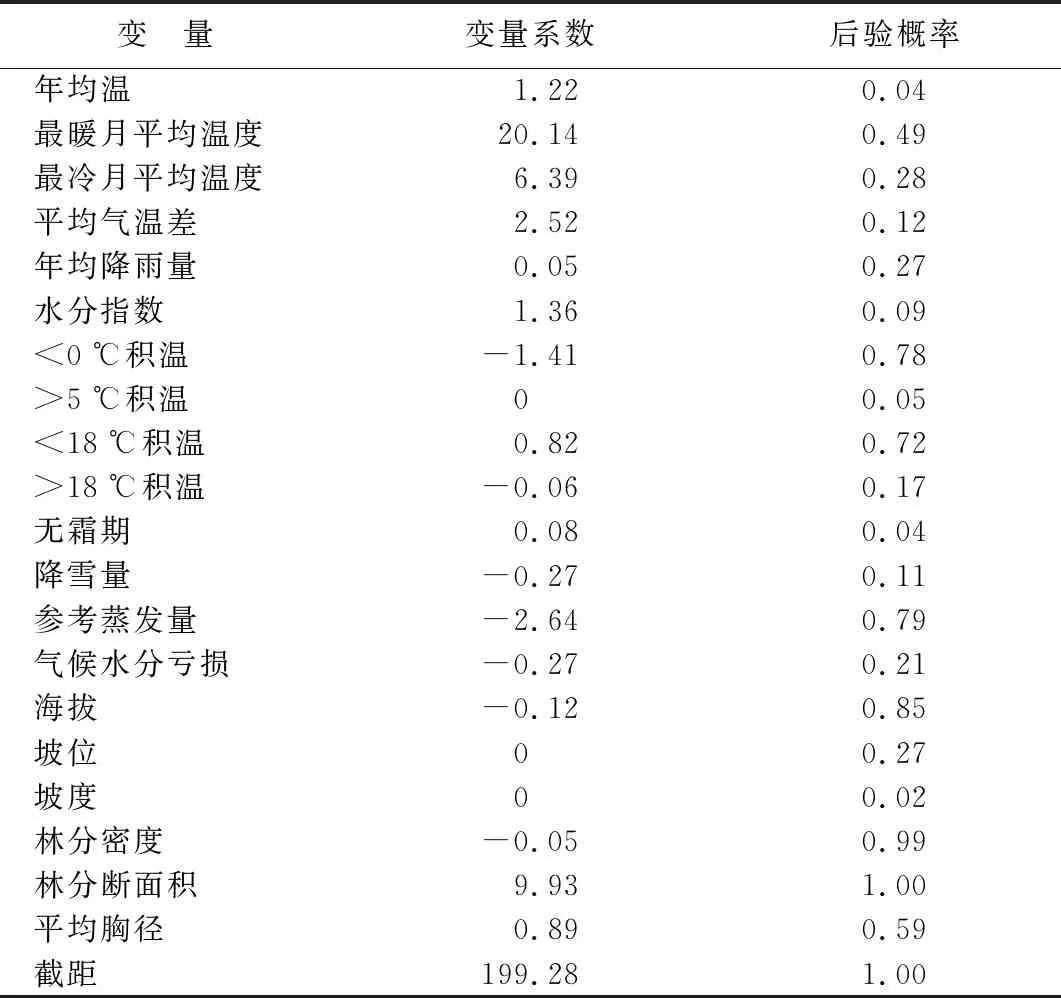
表5 基于贝叶斯模型的参数估计值及后验概率

通过两个模型的对比评价可知，逐步回归的决定系数(R2)为0.95，均方根误差(RMSE)为17.53。而BMA的决定系数(R2)也为0.95，均方根误差(RMSE)为37.51。

图2模型按照后验概率从左侧最好到右侧最差排序，排名在顶部X轴上。模型中排除的变量以黑色显示，而包含的变量则以颜色显示，颜色与对数后验概率相关。每列的颜色与该模型的后验概率(X轴)的对数成正比。由此可知，林分蓄积量模型并非只是一个简单的模型，而是由多种模型组合。

Intercept.截距；aspect.坡位；N.林分密度；Dg.林分平均胸径；MWMT.最暖月平均温度；TD.平均气温差；AHM.水分指数；DD5.>5 ℃积温；DD18.>18 ℃积温；PAS.降雪量；CMD.气候水分亏损。

图3可知，根据BMA方法预测的混交林林分蓄积量残差波动相对平稳，逐步回归预测的林分蓄积量残差波动较大。

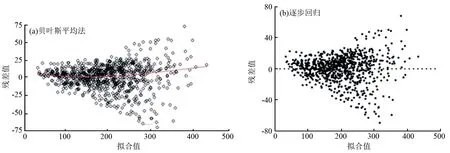
图3 贝叶斯模型和逐步回归法的林分蓄积量残差

4 讨论

本文应用逐步回归法和贝叶斯模型平均法建立了东北针阔混交林蓄积生长模型，对比分析了逐步回归和贝叶斯模型平均法对林分蓄积量的预估效果，进一步分析了贝叶斯模型平均法在模型组合方面的解释的能力。

本文采用了气候因子和林分因子共计21个变量进入模型。在逐步回归中，最终选择坡位、海拔、林分密度、林分断面积、林分平均胸径、最暖月平均温度、<0 ℃积温、<18 ℃积温、参考蒸发9个因子进入模型。在BMA方法中，后验概率高于0.5的只有海拔、林分密度、林分断面积、平均胸径、<0 ℃积温、<18 ℃积温、参考蒸发量等7个变量，说明这7个变量是影响林分蓄积量生长的主要因素。胸高断面积和林分平均胸径与云冷杉针阔混交林蓄积量呈正相关关系，与前人研究结果一致[26-27]。但是林分密度、海拔与蓄积量却呈现负相关关系。这是因为随着海拔增加气温降低，导致树木生长缓慢，林分中小树生长频繁，林分密度不再主导林木生长；由于林木间的竞争关系，随着林分密度的逐渐增大，林木发育逐渐受到抑制，蓄积呈现下降趋势。气候因子方面年均气温温和年降水量对林木蓄积生长影响不显著，因为东北独特的气候条件，巨大的昼夜温差等间接影响林木生长，所以导致<0 ℃积温、<18 ℃积温等与温度相关的因子同时可以影响林木生长发育。因此，在混交林的经营中，应合理调整林分密度及树木径级比例，从而促进树木生长发育。

贝叶斯模型平均法的预测准确率和逐步回归基本一致，一方面是由于逐步回归更容易选择冗余变量，会简单地提升模型拟合效果，但贝叶斯平均法选择的变量更加准确，所选变量更加可靠；另一方面由于总样本量太大，贝叶斯模型平均法的预测准确率没有充分体现，对于小样本数据，贝叶斯方法的性能会显著优于传统方法[28]。另外，逐步回归所确定的模型与贝叶斯模型平均法所确定的前5种模型选择变量不尽相同，因为逐步回归法相对于贝叶斯模型平均法更易选择冗余变量[29]，且逐步回归法忽略了模型的不确定性，造成结果出现差异。贝叶斯模型平均法通过考虑模型的不确定性，将不显著因子剔除，模型结果更加准确可靠。

通过考虑模型的不确定性，贝叶斯模型平均法使模型更加准确。在不显著降低预测精度的情况下，应该考虑如何利用贝叶斯模型平均法更全面地包括所有影响因素且不出现冗余现象是未来研究的方向，同时未来应该偏向小样本数据且可拓展到森林生物量、碳储量等方面进行研究。