基于压缩感知谱反演算法及其在随钻过程中的应用
舒梦珵, 张峰, 邹佳儒, 霍守东*, 罗鸣, 张万栋,李文拓, 穆盛强, 梁瑶
1 中国石油大学(北京)地球物理学院, 北京 102249 2 中国科学院地质与地球物理研究所, 北京 100029 3 中海石油(中国)有限公司海南分公司, 海南海口 570312 4 中海石油(中国)有限公司湛江分公司, 广东湛江 524057 5 中国地质科学院地质研究所, 自然资源部深地动力学重点实验室, 北京 100037
0 引言
南海资源丰富,勘探的开发前景广阔,北部南海莺歌海盆地和琼东南盆地超过75%的地区高温超压地层发育,高温高压天然气资源量大约有4万亿m3的资源量,是我国南海典型的高温高压盆地,也是南海大气区建设和国家南海能源基地建设重点区域(陈多福等,2004; 李绪深等,2017).钻井是超高温高压油气勘探开发的关键环节,是南海资源开发不可缺少的技术.但由于南海地区高温超压地层的发育,在钻井过程中,受关键层位、尤其是薄弱层影响,较易导致井漏、溢流等复杂事故,部分井甚至无法实现钻探目标的精准卡层,会大大增加钻井风险,以致钻井事故频发,给海上超高温高压油气勘探开发带来巨大安全隐患.
目前,通过地震数据进行关键层位及薄弱层识别是最为有效的手段.但由于常规地震数据分辨率不足,在随钻的卡层和风险评估中无法精准识别特殊地层的分布,亟需高分辨率处理技术来提高地震数据的纵向分辨率,从而提高地震数据识别风险的能力(李庆忠, 1993).常规的地震资料高分辨率方法主要有反褶积(章珂等,1999)、时变谱白化(范小冬等,1995)、反Q滤波(姚振兴等,2003;王珺等,2008)和基于反演方法的拓频处理(曹孟起等,2003).虽然上述方法均取得了实际应用效果,但都存在着一些不足.反褶积法地震数据并不能完全满足地层反射系数序列的统计规律和子波相位的前提假设,对高频噪声敏感,因此会影响反褶积方法的应用效果.谱白化法没有考虑子波在传播过程中的时变特性,得到的地震记录结果通常无法保持原始剖面的反射能量相对关系,而且对于能量弱的同相轴效果较差.反Q滤波法需要求出地下地质体的吸收衰减Q因子模型,但实际应用过程中Q因子很难求取准确,极大地限制了该方法在实际资料处理中的应用.拓展频带方法虽然在原理上可以保持地震数据有效的高频成分,恢复的薄层信息相对保真,但其稳定性和可靠性受到参数的影响比较大.常规的谱反演方法通常在L2范数的约束条件下进行求解,提高地震数据分辨率效果有限.针对上述不足,本文选取基于谱反演的方法进行地震数据高分辨率处理,通过利用反射系数的奇偶分解原理(刘建辉等,2018)及偶分量对于薄层分辨能力更高等优点,通过反演方法求解目标函数(刘万金,2013),得到分辨率更高的反射系数.
近年来迅速发展的压缩感知理论(Donoho, 2006; Baraniuk, 2007; Candes and Wakin,2008)给信号带来了新的采集与处理方法.在压缩感知问题中,可以通过求解一个范数的稀疏约束优化问题重建稀疏信号,从而达到保幅、保真提高信号高频信息的目的.但该问题是一个典型的NP难题.有学者为了解决这一问题,提出了一系列的迭代阈值类算法.Blumensath等(2007)提出了硬阈值迭代算法.Mallat和Zhang(1992)提出了匹配追踪(Matching Pursuit,MP)算法,通过从字典矩阵中选择与信号最为匹配的原子构建稀疏逼近,求出信号残差,然后通过迭代选择与残差最为匹配的原子,直到残差满足要求,但该算法收敛需要很多次迭代.Tropp 和Gilbert(2007)针对匹配追踪算法的不足,提出了正交匹配追踪算法,该算法能够确保残差与已选择原子之间的正交性,使得在有限次迭代中达到收敛的效果.Blumensath和Davies(2008)提出了基于贪婪算法的方向追踪法,该算法通过选择合适的方向和步长进行搜索最优解.Needell和Tropp(2009)提出了一种新的迭代重建算法——压缩采样匹配追踪算法(Compressive Sampling Matching Pursuit, CoSaMP),该算法在达到最优化算法的重建精度的同时大大降低了算法的计算复杂度以及计算空间.Foucart(2011)在正交匹配追踪算法和压缩采样匹配追踪算法的基础之上,提出了一种新的求解欠定方程的迭代算法——硬阈值追踪算法(Hard Thresholding Pursuit, HTP),该算法有效提升了计算效率.该类算法还有正则化的正交匹配追踪算法(Regularized Orthogonal Matching Pursuit, ROMP)、改进的后退型OOMP(Improved backward optimized OMP, IBOOMP)等.本文提出将基于压缩感知理论应用于谱反演算法中以实现提高地震数据分辨率的目的.通过对上述稀疏约束优化问题求解方法对比,最终本文选用硬阈值法求解方法直接进行压缩感知L0范数求解,该方法不但可以保持尺度独立,而且还可大大提高算法及信号重建的稳定性.
同时,本文提出了一种稳健的压缩感知谱反演算法及技术流程:首先利用薄层匹配追踪算法求取初始反射系数;在此基础上,进行基于L0范数压缩感知理论的叠后稀疏反演,得到最终反射系数模型;最后基于整形正则化进行子波提取,并进行小波分解以及高频子波替换,以达到保幅、保真地拓展高频,大幅提高地震数据分辨率的目的.将本文方法应用于随钻过程中,不但能够相对保幅、保真地提高地震数据的分辨率,而且还可精细刻画超高温高压关键层位及薄弱层的地震响应特征.
1 基本原理
本文提出了一套基于压缩感知L0范数谱反演算法提高地震数据分辨率方法和实现流程,主要分为如下三个步骤:
(1)基于薄层匹配追踪算法求取地震数据初始反射系数.
(2)在步骤(1)所获得初始反射系数的基础上,进行基于压缩感知L0范数谱反演计算,反演求得最终反射系数.
(3)基于整形正则化进行子波提取,并进行小波分解及高频子波替换,最终实现提高分辨率的目的.
1.1 薄层匹配追踪
薄层匹配追踪有单层假设和双层假设,为了能够提高地震数据的分辨能力,本文采用双层假设匹配追踪算法.假设两个单反射层位于时间ta和tb,反射系数为a和b,对应的初始子波分别为wa和wb,那么,目标函数obj表达为:
obj=min∑(d-awa-bwb)2,
(1)
其中,d为地震记录.对该方程求极值:
(2)
线性方程的解为:
(3)
在初始计算时可以设置零反射系数或随机初始反射系数模型,通过薄层匹配追踪,可以得到初始的反射系数模型,如图1所示.

图1 (a)输入地震剖面;(b)初始反射系数
1.2 基于L0范数压缩感知的叠后稀疏反演
在获得初始反射系数后,文中在求解反射系数的过程中引入L0范数约束,目标函数为
obj=∑(d-a*w)2+λ‖a‖0(a≠0),
(4)
其中,d为叠后地震数据,a为反射系数,w为子波褶积算子矩阵,λ为L0范数的权重,‖a‖0为反射系数L0范数,表示非零值的个数.由于(4)式中L0范数约束的优化问题求解为非凸的,实际计算较为困难,因此我们采用硬阈值算法(Li et al., 2011)直接求解L0范数约束的优化问题.
为对比不同范数约束下目标函数求解的效果,我们将(4)中目标函数的L0范数约束换为L1范数约束及L2范数约束,可得到L1范数约束及L2范数约束的优化问题.采用一道地震数据为例,得到三种范数约束下优化问题求解的反射系数反演结果如图2所示.对比结果表明,相较于L1范数约束和L2范数约束,L0范数结果更加稀疏,信噪比更高,能够得到频带更宽的地震反射系数模型.为进一步提频处理提供较好的结果,随后将匹配追踪结果作为初始输入进行基于L0范数压缩感知的叠后稀疏反演,相关测试结果(图3)表明,相较于匹配追踪的结果,通过L0范数叠后稀疏反演(图3c)结果可以得到更加准确的反射系数.

图2 (a) 输入地震数据反射系数; (b) L0范数反演; (c) L1范数反演; (d) L2范数反演

图3 (a) 输入地震剖面; (b) 匹配追踪结果; (c) 稀疏反演结果
1.3 连续小波变换-Morlet小波
Morlet小波ψ(t)可视为高斯包络调幅下的复正弦函数(Morlet et al., 1982):
(5)
其中σ为Morlet子波的调制频率,通常情况下取值需大于5.33.Morlet子波ψ(t)的傅里叶变换为:
(6)
典型的Morlet小波时间域波形及其振幅谱如图4所示.随后采用地震道的傅里叶变换D(ω)和反射系数傅里叶变换R(ω)优化得到Morlet子波的最优尺度,可通过最小化式(7)的优化目标函数得到最优尺度aopt:

图4 (a) 时间域Morlet小波; (b) 频率域Morlet小波
(7)

(8)
最终利用高频Morlet小波或者其他高频子波ψhigh(t)对ψ(t)进行替换并重构(如图5所示即为一个Morlet子波及一个高频子波),可自然地拓展低、高频能量:

图5 (a) 低频Morlet小波示意图; (b) 替换用Morlet高频小波示意图
(9)
应用上述步骤对图6a所示数据进行处理,得到最终宽频处理结果如图6b所示,可明显提高地震剖面的分辨率.

图6 提高分辨率处理前后对比
基于以上三个步骤,本文形成了基于压缩感知L0范数谱反演提高分辨率技术流程(图7),在技术流程中,为了能够保证子波计算过程中的稳定性,采用整形正则化子波提取方法(Huo,2015),以保证在反射系数较小区域或信噪比较低的地震数据情况下可提高求取子波的稳定性.

图7 基于压缩感知L0范数谱反演提高分辨率技术流程
2 基于压缩感知谱反演算法实际数据试算效果
通过实验数据测试,合成地震记录标定结果(图8)显示,文中提出的提高分辨方法能够相对保幅、保真的恢复原始数据中的高频信息.原始实验数据应用26 Hz雷克子波较好标定,对地层厚度识别能力有限,提高分辨率结果能够应用48 Hz雷克子波进行很好标定,地层厚度识别能力提高一倍.同时,拓频后地震数据的波组特征与合成记录吻合较好(如图8中黑色实线及黑色虚线方框范围显示),很好地保留了原始地震数据波组强弱对应关系,并且相较于原始地震数据,能够突出更为精细的小尺度沉积地层分布规律.

图8 提高分辨率前、后井震标定对比图
另一方面,从测试区的沿T31层位均方根属性(RMS)图可以看出,提高分辨率处理结果(图9b)对于地层、断层和水道体的刻画与原始地震数据基本一致,同时可反映出更多地质体的细节信息(如图9b中黑色圆圈显示区域).由此说明,文中方法在实现了相对保幅、保真提高分辨率目的的基础之上,还能对地震数据中的小尺度地质信息进行精细刻画.

图9 提高分辨率前(a)、后(b)沿T31层段RMS属性切片对比图
3 随钻中实际资料分析
本文在基于压缩感知谱反演算法的基础上,将其应用于随钻过程中的精准卡层识别,并形成针对薄弱层精准卡层识别及薄储层精细深度矫正两项技术流程.
3.1 薄弱层精准卡层识别
文章选取井C进行实际数据试算,井C位于莺歌海凹陷斜坡带南段,主要目的层为黄流组一段和二段,该区存在薄弱层发育,在钻井过程中造成钻井液漏失的复杂情况.
原始数据显示(图10),该区薄弱层主要位于区域地震反射T31(蓝色层)与强波峰(绿色层)位置中间,为复合波谷或中强波峰反射特征,由于研究区地震数据频率较低,常规数据处理方法得到的处理成果不能有效地对超高温高压薄弱层进行单独识别.

图10 原始地震数据薄弱层空间分布示意图
利用文中方法对现有地震数据进行保幅、保真高分辨率处理,如图11所示通过井C合成记录标定后的井旁道分析,原始数据复合波谷处薄层及其空间分布范围得到有效分离,钻井证实该套薄层为薄弱层,该处发生钻井液漏失的钻井复杂情况.

图11 提高分辨率前、后井的合成地震记录对比图
文章通过研究区多井纵波阻抗和密度曲线的交会,进一步开展岩石物理分析(图12).通过岩性的标定,确定了图中红色方框内为砂体阻抗及密度分布范围.进一步,将漏失段多井测量的阻抗和密度值在交会图中标出,范围为图中紫色方框区域,揭示了试验区薄弱漏失层波阻抗的数值分布范围(阻抗值9300~11400 m·s-1·g·cm-3).基于此结果可以半定量的刻画出工区内实验井薄弱层漏失的空间分布范围.
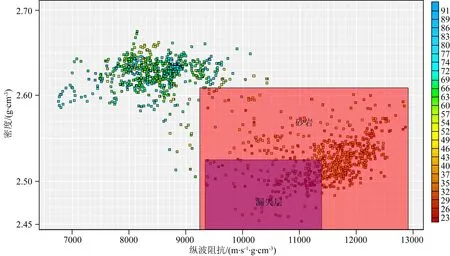
图12 三口实验井波阻抗-密度测井曲线交会图
拓频前后反演结果对比(图13)表明,拓频后反演结果能够很好地反映出薄弱层的反射特征,与已知钻井岩性信息吻合;拓频后反演数据纵向分辨率提高,横向连续性增强,通过反演的波阻抗数据标定,大大提高了砂体薄弱层及漏失区域的可追踪性及可识别性.
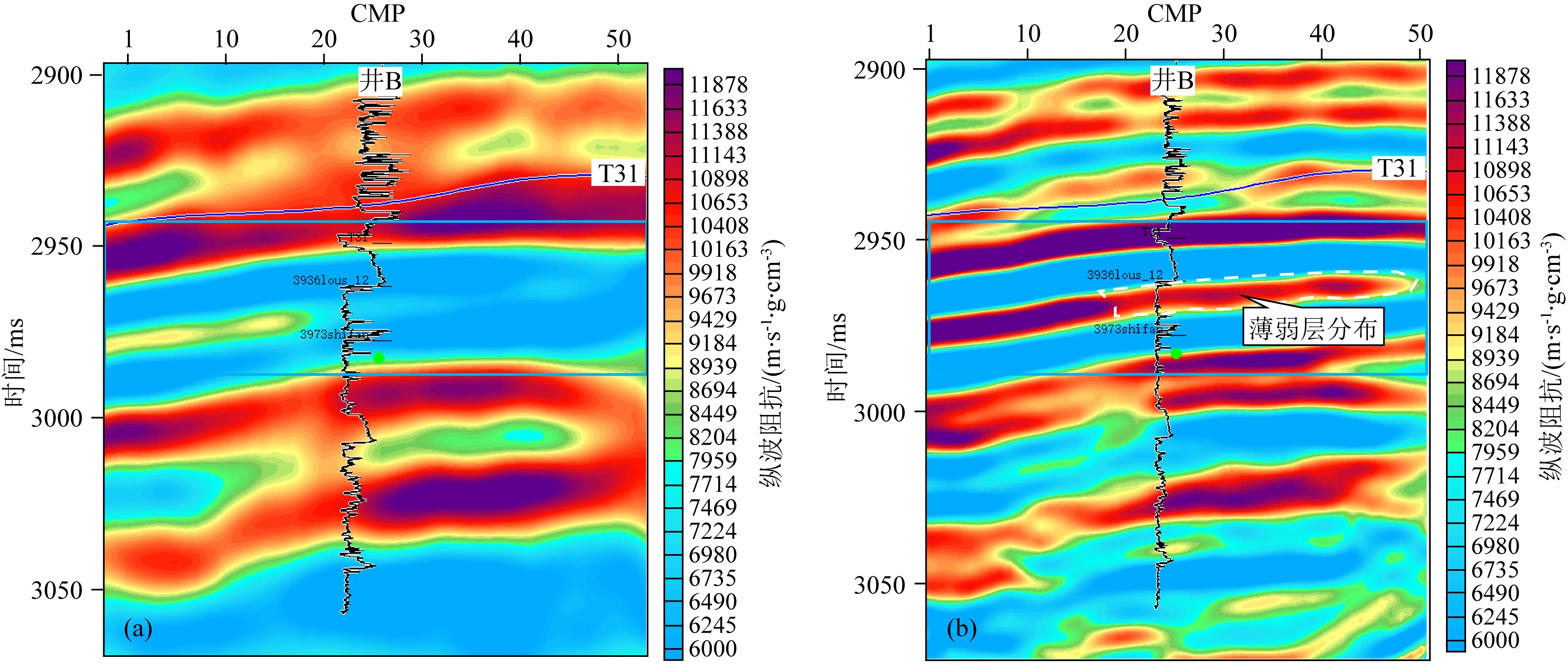
图13 提高分辨率前(a)、后(b)过井反演剖面对比
通过上述的分析,文中总结了高精度薄弱层识别卡层的技术流程如图14所示.
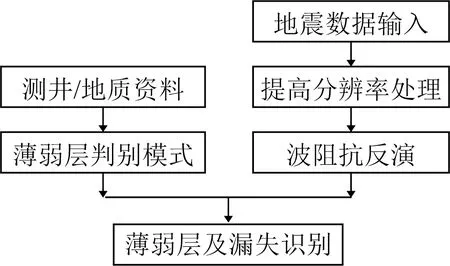
图14 高精度薄弱层识别技术流程
3.2 薄储层精细深度矫正
文中选取莺歌海盆地乐东区中央底辟带的测试数据,进行薄储层精细刻画及深度矫正实际数据计算,测试目标区主要目的层为黄流组一段,发育多套薄砂体沉积,现有地震数据难以精确识别砂体分布.井D为该区一口探井,在随钻过程中对砂体深度的精准卡层预测,可以有效指导施工方案调整,为钻井安全实施提供依据.
原始数据显示(图15a)该区砂体储层主要位于区域地震反射T30(黄色层)下覆,为复合波反射特征.由于研究区地震数据频率较低,常规数据处理方法得到的成果剖面无法对目标井黄流组一段(N1hl1-B至N1hl1-C)中三套主力砂体进行刻画.而提高分辨率数据结果(图15b)可以清楚的突显出复合波组中薄砂体的空间分布.

图15 提高分辨率前(a)、后(b)目标井D过井地震偏移剖面对比图
基于提高分辨率数据进行地震反演(图16)可以看到,原始数据的反演结果无法对井D的三套主力砂体有效刻画(图16a,暖色为砂体波阻抗特征),而基于本文提高分辨率数据得到的高精度反演结果能够清楚地反映三套砂体的空间分布及相互间的交接关系(图16b,暖色为砂体波阻抗特征),其中可识别砂体的最小厚度为二号砂体13 m.
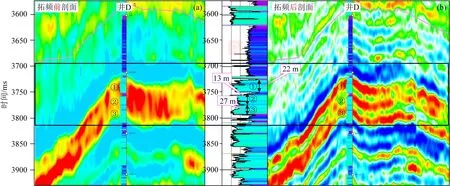
图16 提高分辨率前(a)、后(b)目标井D过井波阻抗反演剖面对比图
另外,在T30反射层的上覆,与原始地震数据相比,提高分辨率之后的数据能够很好的突出莺歌海组二段N2hgh2-A层和N2hgh2-B层的反射特征,从剖面上看(图17b),这两层在提高分辨率剖面上表现为中弱振幅连续反射特征,全区可追踪.由于原始数据在T30反射层前无法进行深度标定卡层,在钻遇T30时,钻遇地层深度与预测深度的误差为20 m,而通过提高分辨率数据,可以在钻遇T30前,通过N2hgh2-A层和N2hgh2-B层进行深度标定,在钻遇T30储层顶时,钻遇地层深度与预测深度的误差仅为8 m,预测误差为2.2‰(图17c).

图17 提高分辨率前(a)、后(b)—(c)目标井D井深度识别误差对比图
通过随钻过程中对砂体深度的精准卡层预测的应用,文章提出了高精度薄储层识别及精准卡层技术流程(图18),实现了随钻过程中的精准卡层及薄储层识别,为钻井过程中的风险评估和钻井方案的调整提供了可靠依据.

图18 高精度薄储层识别及精准地层识别技术流程
4 结论与展望
本文系统的论述了目前主流的提高分辨率处理方法和压缩感知算法的研究现状及方法优势,提出了基于压缩感知谱反演算法提高分辨率技术及计算流程,并将该技术应用于随钻过程精准卡层及风险层评估的应用中,取得了较好效果.
文中提出的基于压缩感知L0范数谱反演算法,可以较好的实现反射系数的求解,对弱反射系数有更好的保护性.同时,基于该算法的计算流程,可以有效的保证L0范数求解反射系数过程中的计算稳定性,提高计算迭代效率,实现相对保幅、保真的提高地震数据分辨率的目的.
该算法在超高温高压随钻过程的实际数据计算中,通过对实际地震数据保幅、保真高分辨率处理,有效的识别了随钻过程中钻遇的关键层位(尤其是薄弱层)的地震响应特征及空间分布规律.并且,文中针对薄弱层和薄储层精准卡层的情况提出了针对性的计算流程,在实际数据应用中取得了较好的应用效果.
该方法在随钻过程中的应用,可以有效避免因为薄弱层难以识别及关键层位卡层不准而引起的钻井事故和经济损失,为南海西部油田超高温高压钻井的安全生产及钻井方案的调整提供保障.
致谢感谢审稿人和编辑对本文提出的宝贵修改建议.

