475型静态推靠式旋转导向钻具组合的弯曲应力分布规律

贾建波， 兰洪波， 菅志军， 张玉霖， 孙师贤， 孟巍

中海油田服务股份有限公司， 北京 101149

0 引言

旋转导向钻井系统(Rotary Steerable drilling System，RSS)是定向钻井的核心装备，也是高难度定向钻井的必备利器(张绍槐，2003；王鹏等，2013；Jerez and Tilley，2014).经过多年努力，目前国内三大石油公司均研制出了675型静态推靠式旋转导向钻井系统(导向头直径6.75 in，适用井眼φ215.9 mm左右)(菅志军等，2017；冯定等，2021；赵文庄等，2021).不仅如此，中海油服油田技术研究院还率先研制出了475型静态推靠式旋转导向钻井系统(导向头直径4.75 in，适用井眼φ152.4 mm左右)；2019年实钻最高造斜率达到14.31°/30 m(尚捷等，2021)；2021年实钻最高造斜率突破20°/30 m.与675型旋转导向钻井系统相比，475型旋转导向钻井系统适用于小井眼定向钻井作业，普遍要求实钻最高造斜率应达到15°/30 m以上.现有研究成果表明，在高造斜率井眼中旋转钻进时，钻具组合的弯曲应力较大，疲劳失效风险较高(Wu，1996；朱全塔等，2014).近年来，国内钻井现场已经多次发生静态推靠式旋转导向钻井系统的导向头芯轴和挠性短节断裂事故(进口及国产系统均有发生)，亟需开展事故原因分析及对策研究.

鉴于此，以中海油服475型静态推靠式旋转导向钻井系统为例，建立旋转导向钻具组合(Rotary Steerable Bottom-Hole Assembly，RSBHA)力学分析模型，模拟分析RSBHA的弯曲应力总体分布规律、最大弯曲应力变化规律，为提升该系统的造斜能力和降低疲劳失效风险提供支持.

1 RSBHA力学分析模型

1.1 RSBHA的基本形式

RSBHA基本形式见图1，自左而右依次为钻头、导向头模块、挠性短节、供电通讯模块.此外，有时还在稳定器和挠性短节之间安放近钻头伽马短节；为了保护供电通讯模块，有时还在该模块上安放第2个稳定器.

图1 475型静态推靠式RSBHA

1.2 底部钻具组合力学模型

目前有多种方法建立下部钻具组合受力分析模型，包括有限元法(Akgun，2004)、有限差分法(杨东全，2003)、纵横弯曲梁法(唐雪平，2011；唐雪平等，2013；洪迪峰等，2014；史玉才等，2018)等.综合考虑建模和求解难度，以及计算精度要求，此处选择纵横弯曲连续梁方法建立RSBHA力学分析模型.其中，对导向头、导向翼肋和挠性短节进行等效处理是关键.

如图2所示，基于静态推靠式旋转导向钻井系统的结构及工作原理，将导向翼肋等效为偏心稳定器(该处支撑力等于导向合力，内弯矩和偏心位移均未知)，并以该偏心稳定器为支点将导向头分成两跨梁；借鉴变截面梁等效处理方法，将挠性短节的两个台阶面均等效为“虚支座”(该处内弯矩、偏心位移均未知).经过上述等效处理，整个RSBHA由6个支座(钻头、导向翼肋、稳定器、挠性短节的两个台阶面、上切点)、5跨纵横弯曲梁组成.其中，钻头中心至导向翼肋中心为第1跨梁；导向翼肋中心至稳定器中心为第2跨梁；稳定器中心至挠性短节下台阶面为第3跨梁；挠性短节下台阶面至上台阶面为第4跨梁；挠性短节上台阶面至井壁切点为第5跨梁.设钻头外径为Db，稳定器外径为Ds1；第i跨梁长度为Li(i=1～5)、外径为Dci、内径为di.

图2 475型静态推靠式RSBHA力学分析模型

以二维圆弧井眼为例，应用纵横弯曲连续梁理论直接给出各个支座对应的三弯矩方程组(式(1)—(2)；将导向翼肋等效为偏心稳定器，利用该处“支撑力等于导向力合力”这个补充条件，可以建立第1个补充方程(式(3))；将挠性短节的两个台阶面均等效为“虚支座”，利用“台阶面左右两侧剪力相等”这个补充条件，可以建立2个补充方程(式(4)).

(1)

(2)

(3)

(4)

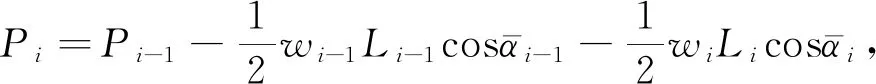
(5)

(6)

(7)

(8)

M5=EI5K.

(9)

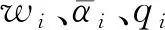
式(1)—(4)即为475型静态推靠式RSBHA力学模型对应的基本方程组，共有8个基本方程、8个基本未知数，需要采用数值求解方法.其中，基本未知数包括：导向翼肋处内弯矩M1和偏心位移Δ1(Δ1隐含于支座高度y1中)，稳定器处内弯矩M2，挠性短节台阶面处内弯矩M3(下台阶)和M4(上台阶)，偏心位移Δ3和Δ4(Δ3、Δ4分别隐含于支座高度y3、y4中)，切点位置L5(最后一跨梁长度).

1.3 弯曲应力计算方法

求解上述基本方程组之后可以计算出各跨梁对应的弯曲应力，计算步骤如下：

(1)利用上述基本方程组(1)—(4)求出切点位置L5(最后一跨梁长度)、各个支座对应的内弯矩Mi(i=1～4)和偏心位移Δi(i=1，3，4)；

(2)应用纵横弯曲梁基本理论(白家祉和苏义脑，1990)，依次求出各跨梁对应的挠度函数fi(s)、曲率函数f′i(s)；

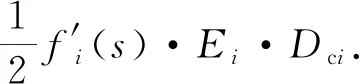
2 弯曲应力总体分布规律分析

以中海油服475型静态推靠式旋转导向钻井系统为例.限定钻头直径152.4 mm、导向合力20 kN、钻压20～50 kN、当前弯曲井段的平均井斜角30°、井眼曲率(10°～18°)/30 m，模拟计算结果见图3.该钻具组合的弯曲应力总体分布规律如下：

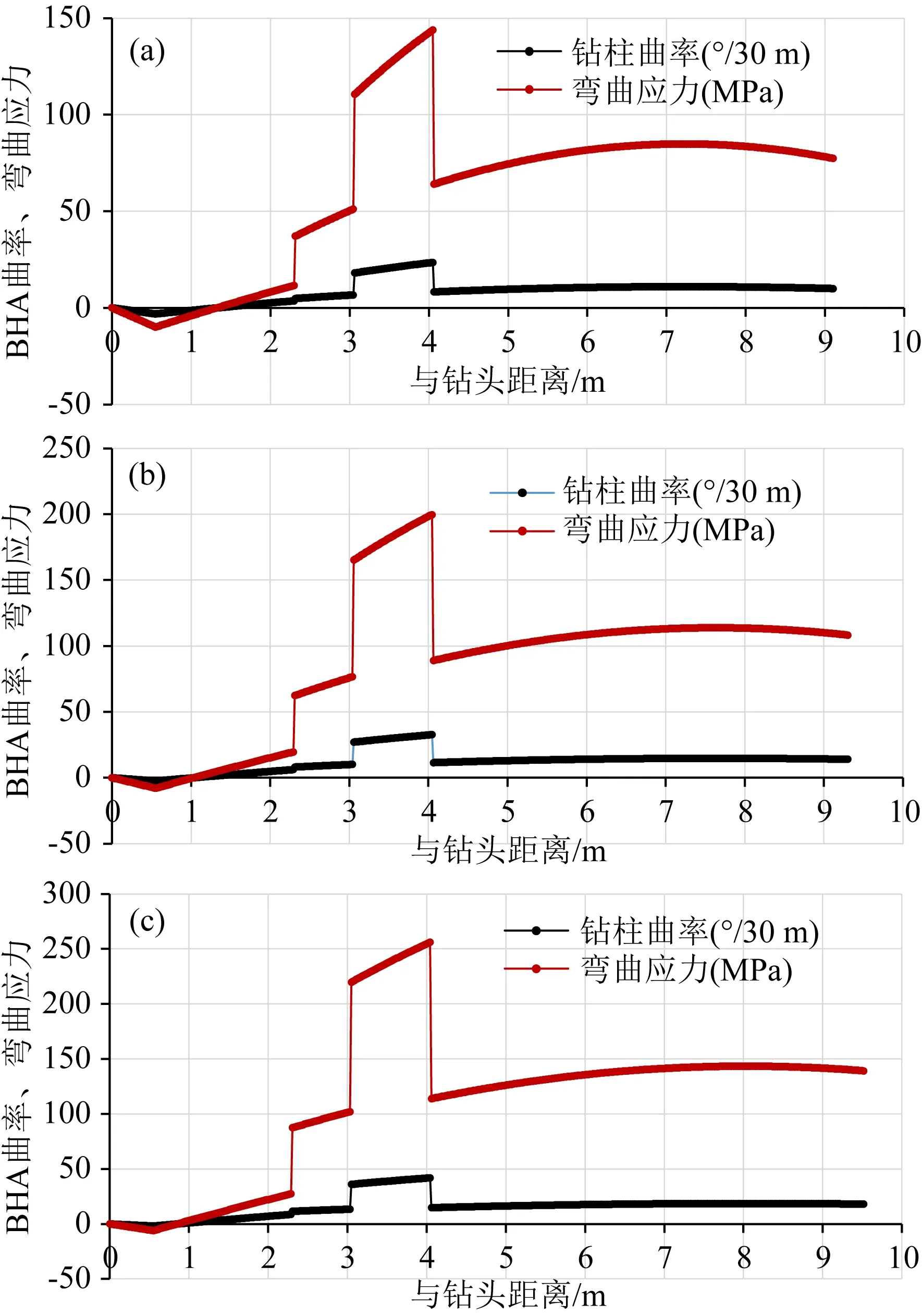
图3 475型静态推靠式RSBHA的弯曲应力总体分布规律

(1)导向头模块(钻头至稳定器)的直径较大、刚度较大，不容易变形，该部分钻柱曲率远小于当前井眼曲率；相应地，导向头芯轴对应的曲率和弯曲应力也比较小.

(2)挠性短节模块的直径最小、刚度最小，最容易变形，该部分钻柱曲率和弯曲应力总体上远大于其他部分；最大曲率和弯曲应力位于挠性短节上台阶面处；最大曲率约为井眼曲率的2～2.5倍.井眼曲率(16°～18°)/30 m时，该部分钻柱的最大弯曲应力约为200～250 MPa.

(3)供电通讯模块的直径和刚度、曲率和弯曲应力均介于导向头模块和挠性短节模块之间；该部分钻柱的最大曲率和弯曲应力位于挠性短节上台阶面与上切点之间；最大曲率稍大于井眼曲率.井眼曲率(16°～18°)/30 m时，该部分钻柱的最大弯曲应力约为125～150 MPa.

3 最大弯曲应力变化规律分析

上文分析表明，现有475型静态推靠式RSBHA的最大弯曲应力位于挠性短节上台阶面处.限定导向头结构参数不变，此处重点分析挠性短节有效长度、钻压、井眼曲率对最大弯曲应力影响规律.

3.1 井眼曲率

限定挠性短节有效长度L4=1.0 m、导向合力20 kN、钻压20 kN，RSBHA的最大曲率及弯曲应力随井眼曲率变化规律见图4.可以看出，最大曲率及弯曲应力随井眼曲率增大而显著增大，并近似呈线性变化.

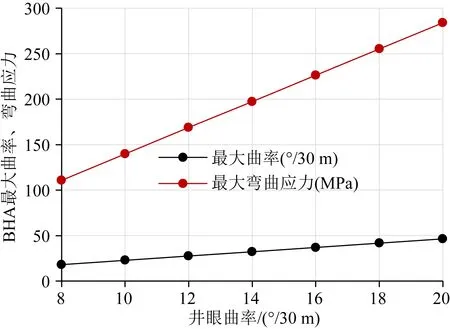
图4 最大弯曲应力随井眼曲率变化规律

上述分析还表明，475型静态推靠式RSBHA的最大曲率约为井眼曲率的2.0～2.5倍，井眼曲率大于16°/30 m时RSBHA的最大弯曲应力大于200 MPa，远高于直接采用井眼曲率所计算出的弯曲应力值.

3.2 挠性短节有效长度

挠性短节有效长度是指挠性短节上、下台阶面之间的距离，也就是上述旋转导向钻具组合力学模型中第4跨梁的长度L4.

限定导向合力20kN、钻压20kN、井眼曲率16°/30 m，RSBHA的最大弯曲应力随挠性短节有效长度L4变化规律见图5.可以看出，在给定条件下，最大弯曲应力随挠性短节有效长度增大而明显减小.

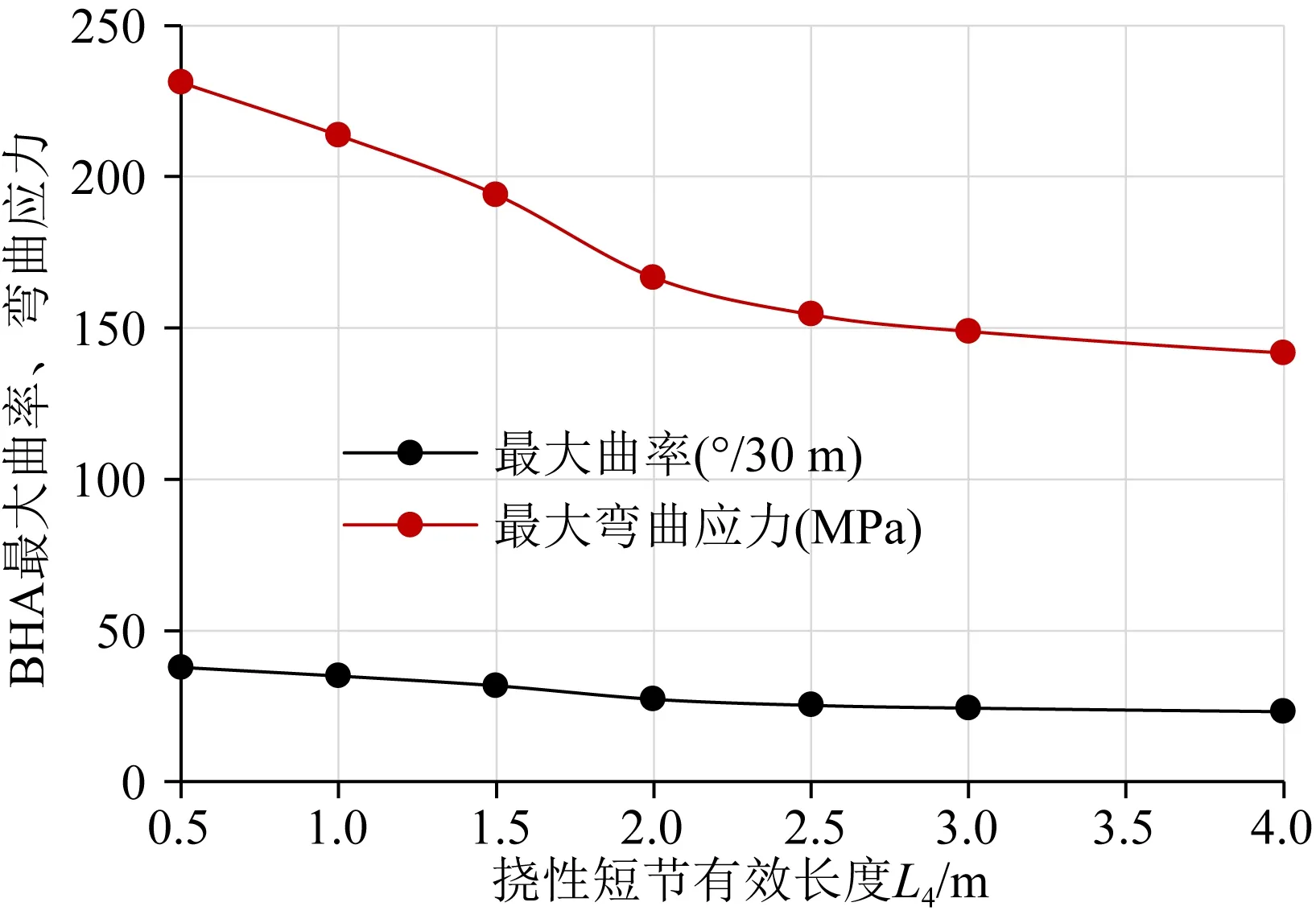
图5 最大弯曲应力随结构参数L4变化规律

上述分析表明，限定井眼曲率条件下，适当加长挠性短节有助于降低RSBHA的最大弯曲应力.此外，适当加长挠性短节还有助于提高造斜率.但是若继续加长挠性短节，挠性短节将会与井壁接触.模拟计算分析表明，当L4≥5.75 m时挠性短节与井壁接触.该情况下造斜率会降低，最大弯曲应力和疲劳失效风险会增大.因此，对于475型静态推靠式RSS来说，为了确保高造斜率且有助于降低RSBHA的最大弯曲应力，推荐挠性短节有效长度L4=1.5～3.0 m.

3.3 钻压、导向合力

限定挠性短节有效长度L4=1.0 m、导向合力20 kN、井眼曲率16°/30 m，RSBHA的最大弯曲应力随钻压变化规律见图6.可以看出，在给定钻压范围内，RSBHA的最大弯曲应力随钻压增大而稍增大.

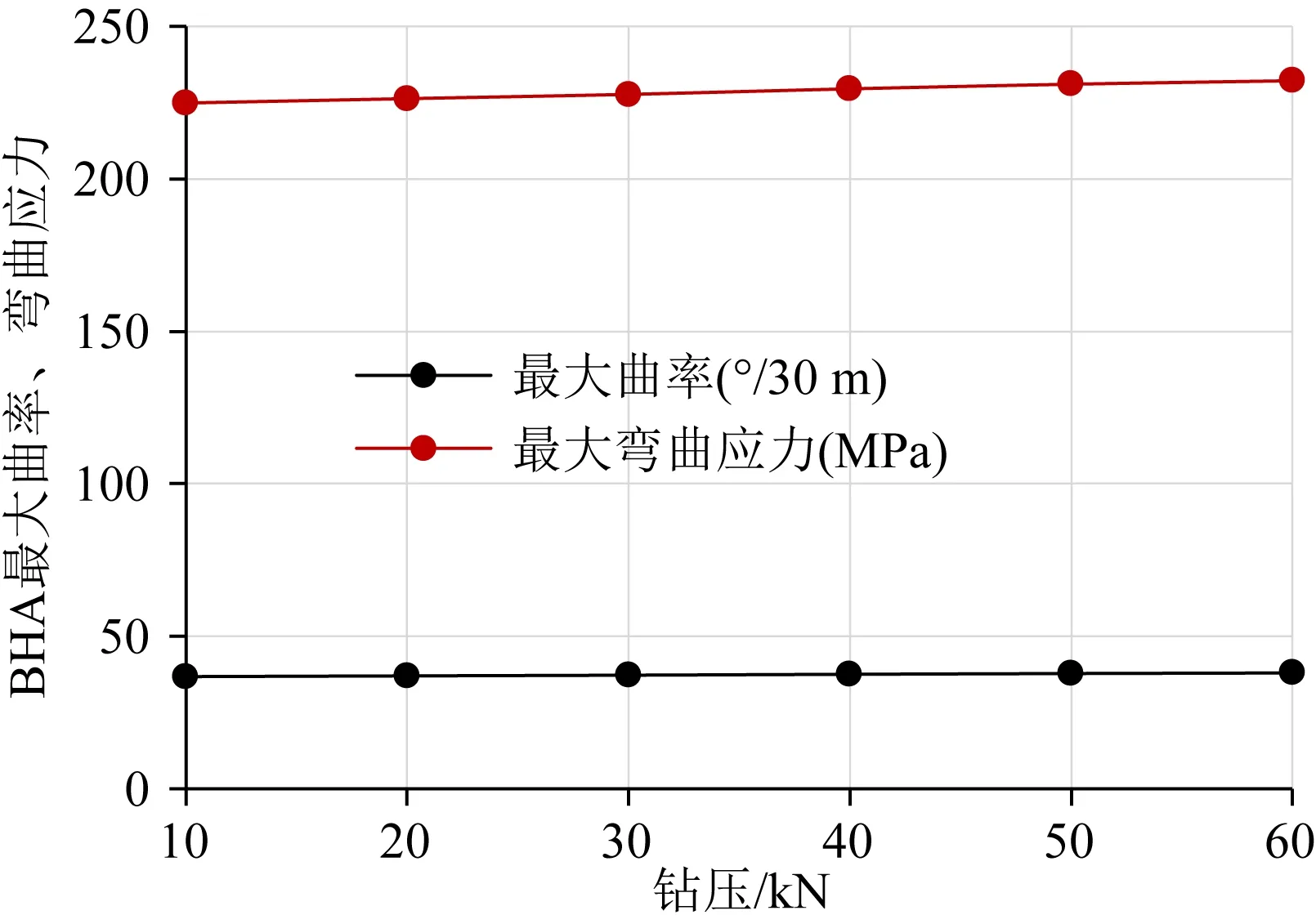
图6 最大弯曲应力随钻压变化规律

上述分析表明，限定井眼曲率条件下，钻压对475型静态推靠式RSBHA的最大弯曲应力影响较小.事实上，给定导向合力条件下，该系统的造斜率随钻压增大而显著减小，随钻压减小而显著增大(王恒等，2018；王恒，2019；滕志想，2020).该情况钻压显著影响新钻井眼曲率，显著影响RSBHA的最大弯曲应力.因此，对于现有475型静态推靠式旋转导向钻井系统来说，为了确保高造斜能力并有助于降低RSBHA的最大弯曲应力，推荐工作钻压30 kN左右.

此外，在给定钻压情况下，造斜率和新钻井眼曲率随导向合力增大而显著增大，随导向合力减小而显著减小.该情况下导向合力显著影响造斜率和井眼曲率，最终显著影响BHA的最大弯曲应力.

4 结论及建议

建立和求解了475型静态推靠式旋转导向钻具组合力学分析模型，模拟分析了该钻具组合的弯曲应力分布规律.基于模拟计算分析结果，给出以下结论：

(1)导向头芯轴的曲率和弯曲应力均比较小；挠性短节的曲率和弯曲应力总体上最大，最大曲率约为井眼曲率的2.0～2.5倍(通常位于挠性短节上台阶面处)；供电通讯模块的曲率和弯曲应力也较大，最大曲率稍大于井眼曲率.

(2)下部钻具组合的最大曲率和弯曲应力随井眼曲率增大而显著增大；限定导向头结构参数条件下，适当加长挠性短节并合理调控钻压和导向合力有助于提高造斜率并降低BHA最大曲率和弯曲应力.

(3)建议考虑钻柱旋转、螺纹及变截面处应力集中影响，继续深入探讨475型旋转导向钻具组合的疲劳失效风险及对策.

致谢感谢中国科学院地质与地球物理研究所智能导钻技术装备体系与相关理论研究团队为本研究提供支持和帮助，并向匿名审稿人提出的宝贵修改意见表示衷心的感谢.