低纬度磁异常的初始模型约束全卷积神经网络化极方法

张志厚， 刘慰心， 石泽玉， 张健， 路润琪，谢小国， 徐正宣,5， 张天一

1 西南交通大学地球科学与环境工程学院，成都 611756 2 西南交通大学， 高速铁路线路工程教育部重点实验室， 成都 610031 3 四川省华地建设工程有限责任公司， 成都 610081 4 四川省地质矿产勘查开发局成都水文地质工程地质中心， 成都 610081 5 中铁二院成都地勘岩土工程有限责任公司， 成都 610000

0 引言

磁异常化极(Reduction to the pole, RTP)是磁测数据处理与解译的重要基础工作，其过程是将任意磁化倾角的磁异常换算成垂直磁化方向的磁异常，其目的是将磁异常的峰值换算到异常体的正上方，使其形态简单化.化极可增强磁异常与场源分布的对应关系，有利于地质解译，甚至可以直接利用化极磁异常识别构造界限、圈定岩体范围、划分沉积盆地规模等(姚长利等, 2003; 骆遥, 2013; 荆磊等, 2017).

磁异常化极大体上可以分为空间域与频率域两类方法.空间域方法是基于等效源思想(Silva, 1986; Li and Oldenburg, 2001; 骆遥和薛典军, 2009; Zuo et al., 2021)，需要先求解等效源的大型线性方程组，然后在垂直磁化条件下再对等效源进行正演获得化极结果.等效源方法的主要缺点是计算时间长，且最终的RTP效果受到“源”的类型、个数、深度及其组合的影响.由于频率域化极原理清晰(Bhattacharyya, 1965)、易于实现、计算效率高，并且在很多情况下取得了较好的应用效果，使得此类方法成为化极常用方法.但在低纬度及赤道地区，频率域化极因子具有明显的放大作用(姚长利等, 2012)，化极计算不稳定.因此，诸多学者都基于化极因子的改进进行了相关研究，如滤波法(Hansen and Pawlowski, 1989; Kis, 1990; Keating and Zerbo, 1996)、泰勒级数法(Hao et al., 2018)、压制因子法(姚长利等, 2003)、非线性阈值法(Zhang et al., 2014)、阻尼法(林晓星和王平, 2012; 荆磊等, 2017)、伪倾角法(MacLeod et al., 1993; Li, 2008; 石磊等, 2012)等.以上方法虽各具有一定优势，也取得了较好地应用效果，但上述方法仍然存在一些问题与不足(姚长利等, 2012)，并且其计算结果还是难以达到精准地球物理勘探阶段科技工作者更高的期望(滕吉文, 2021).

深度学习(Deep Learning, DL)是深度神经网络的简称，是传统人工神经网络的扩展，其包含了更深的隐含层(LeCun et al., 2015).DL并不代表一个单一的算法，而是具有不同网络架构的大类方法总称，其包含监督、半监督和无监督方法.网络架构包括多个处理层和非线性转换层，每一层输出都作为下一层输入.十多年以来，随着大数据可利用性增强，以及在计算机性能日益强大的推动下，DL已经攻克了之前许多无法实现的任务，尤其是在图像语义分割(Krizhevsky et al., 2012)、语音识别(Hinton et al., 2012)和文本翻译等方面上取得了惊人的表现.随后DL的应用场景不仅拓展到了诸多自然科学领域(Dargan et al., 2020; Meade, 2019; Reichstein et al., 2019; Runge et al., 2019; Lai et al., 2020; Schoppe et al., 2020; Andersson et al., 2021; Cheng et al., 2021)，而且在日常生活中的应用也无处不在，如自动驾驶(Grigorescu et al., 2020)、深度伪装(Xiao et al., 2020)、虚拟私人助理等.DL作为一种相对于传统数据驱动的新技术，已被证明具有准确预测复杂系统状态和缓解“维数诅咒”的潜力.因此，DL也给地球物理数据处理带来了许多机遇，如利用训练人工合成数据集的DL网络可进行重、磁(张志厚等, 2021a,b; Yang et al., 2022)、电磁(Puzyrev, 2019; Moghadas, 2020; Liu et al., 2021d)、直流电法(Liu et al., 2020a; Shahriari et al., 2020)、地震(Li et al., 2020; Russell, 2019; Zhang and Alkhalifah, 2019; Liu et al., 2021b; Zhang et al., 2021a)、面波频散曲线(Aleardi and Stucchi, 2021; 张志厚等, 2022a )、探地雷达(Xie et al., 2020; Zhang et al., 2020; Leong and Zhu, 2021; Liu et al., 2021a)反演，利用训练人工标注数据集的DL网络进行余震预测(Fang et al., 2017; Meade, 2019)、以及与计算机视觉相关的地质地球物理自动化解译(Ishitsuka et al., 2018; Qian et al., 2018; Xiong et al., 2018; Li et al., 2019; Shi et al., 2019; Wu et al., 2019a,b; 冯德山和杨子龙, 2020; Liu et al., 2020b; Dai et al., 2021; Garg et al., 2021; 芦凤明等, 2022; 杨晶等, 2022; 张志厚等, 2022b)等.而且DL将极有可能成为地球科学时空结构分类与预测的主要方法(Reichstein et al., 2019).

然而，上述方法一是在训练和预测阶段只采用了地球物理响应数据作为输入，没有地质地球物理模型的理论基础，使得纯数据驱动方法处理结果存在不确定性；二是人工合成数据的标签具有局限性，并且有限人工标签数据也存在一定偏差，使得这些方法并没有较好的泛化能力(Bergen et al., 2019)；三是缺乏样本数据场景外的通用性，即DL的“黑盒”网络结构往往会拟合到一些非重要特征，导致该网络结构会局部塌陷到一些不好的特征上，反而未充分提取数据的主要目标特征，致使“黑盒”网络结构只能对样本数据集类似的数据进行精准预测.故而，亟需一种新方法去结合数据驱动方法和先验知识从而提高地球物理数据处理的稳定性和精度.并且在观测数据的基础上提供强大先验信息约束也许是成功应用深度学习的挑战与途径(Reichstein et al., 2019).

最近，Zhang等(2021b)研究了一种基于先验模型约束的叠后地震数据DL岩性/流体分类预测方法，随后又提出了一种基于地质背景模型约束的地震DL反演方法(Zhang et al., 2021a)，该方法获得结果相比纯数据驱动方法结果精度更高；Wu等(2021)将初始阻抗模型和地震数据作为DL网络的输入，获得了更加稳定与横向一致性较强的阻抗信息；Hou等(2021)实现了一种基于感知信息和先验信息约束的数字岩石DL图像语义超分辨率分割方法.时至如今，基于先验信息DL计算的落地案例不断丰富，不仅在地球物理领域中持续研究，在其他学科的研究中也被报道出来，如水文(Daw et al., 2021)、气候(O′Gorman and Dwyer, 2018)、生物(Peng et al., 2021)、医学成像(Liu et al., 2021c)等.这些研究将为磁异常化极带来了更为广泛的应用潜力，并期望在样本数量少的情况下获得更好的预测精度，以及在样本外场景下具有一定的通用性.

基于此，本文提出一种基于初始模型约束的低纬度磁异常全卷积神经网络(Fully Convolutional Network, FCN.FCN是一种典型的DL网络结构)化极方法.文中采用磁异常快速正演(张志厚等, 2021b)结合磁异常频率域换算(姚长利等, 2003)获取样本数据集，文中不仅将低纬度磁异常作为FCN的输入，而且将初始模型也加入到FCN网络的输入端，初始模型相当于一种低频背景趋势，是通过磁异常频率域换算获得，输出端为异常体模型垂直磁化下的磁异常.在此需要说明低纬度磁异常与化极后磁异常具有近似“180°倒相”关系(方迎尧等, 2006)，或者通过压制因子法或阻尼法也能获取相似的低频背景趋势，因此磁异常化极的初始模型相比其他地球物理线性反演(如重、磁、电物性反演)所需的初始模型更加容易稳定获取，这也是本文能够将先验知识融入FCN网络的关键步骤；此外，文中将含随机噪声的部分合成数据扩展到样本数据集中，类似的策略也被应用到地震阻抗反演(Puzyrev et al., 2019; Zhang et al., 2021a)中，并获得了更好的泛化性能.文中DL网络结构采用简化的FCN骨干结构(张志厚等，2022b).最后，对本文所提方法进行理论数据和实测数据的检验，以此来证实的文中方法的可行性、有效性和适用性.

1 磁异常FCN化极方法

1.1 磁异常化极问题描述

磁异常化极是指任意磁化方向磁异常u0换算成垂直磁化方向磁异常up的一种计算，假设地磁场方向与磁化方向一致，在空间域用式(1)表示化极换算关系：

up(x,y)=φ[u0(x,y)]，

(1)

式中，x,y表示水平位置坐标.

式(1)关系复杂，而在频率域中较为简单，可用式(2)表示(姚长利等, 2003)：

Up(kx,ky)=H(kx,ky)·U0(kx,ky)，

(2)

式中，Up(kx,ky)与U0(kx,ky)分别为up(x,y)与u0(x,y)的傅里叶变换，kx,ky分别为x,y方向的圆频率，H(kx,ky)为：

(3)

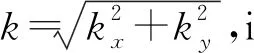
式(3)的极坐标表达式只与角度α有关，如下所示：

α=tan-1(ky/kx)，

(4)

H(α)=[icosI0cos(α-D0)+sinI0]-2，

(5)

在低纬度或者赤道区域，I0→0，并且当α→D0±90°时，H(α)→∞.

在实际计算中，一是数值的有限性存在误差，二是数据的有限性和离散性造成频谱的误差，而造成化极运算不稳定的主要因素是以上误差会被化极因子H(α)放大传递，且放大结果有时候是巨大的、发散的.因此，常用的化极方法是基于对H(α)的改造而进行的.

骆遥和薛典军(2009)考虑了式(2)的另外一种形式(“狭义化赤”)：

(6)

式(6)表示将垂直磁化方向的磁场(化极结果)换算为任意倾斜磁化方向，不同于传统意义上的“化赤”概念(换算为水平磁化方向)，化赤算子为：

SRTE=[icosI0cos(α-D0)+sinI0]2，

(7)

式(7)稳定，表明“狭义化赤”一种稳定的计算过程，其相对于“化极”是一种逆运算.在空间域表达式为：

u0(x,y)=ψ[up(x,y)].

(8)

因此，可以用残差ε作为化极的目标函数，ε为：

(9)

1.2 模型约束的FCN磁异常化极

基于FCN的磁异常化极，是将任意磁化方向的磁异常u0作为输入，垂直磁化方向的磁异常up作为输出(标签)，建立监督学习模型，目的是利用训练好的非线性网络映射函数实现u0到up的预测(转换).传统的FCN预测的目标函数如下所示：

(10)

式中，Θθ为将任意磁化方向磁异常u0转换为垂直磁化方向磁异常up的非线性映射函数，θ为待优化的FCN网络结构参数集(如权重、偏置等网络参数).磁异常化极FCN网络训练的目标就是求取非线性映射函数Θθ(即网络参数调优).Θθ也就是FCN磁异常化极运算函数，其等价于式(1)的运算.

在数学上，低纬度磁异常化极计算本质是位场低频、高频数据转换的问题.高频数据转向低频数据相对比较稳定(如去噪声)，但低频数据转向高频数据则存在不确定性，即使是监督类FCN方法也只能对相似样本数据具有较高的预测精度，缺乏样本数据场景外的通用性；此外，样本数据的有限性也降低了FCN的泛化性能.为了克服这些问题，本文提出了一种新的具有初始模型约束的磁异常化极FCN网络结构，该网络结构将初始模型加入到目标函数中，如下所示：

(11)

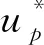
图1所示为本文基于初始模型约束的低纬度磁异常FCN化极流程.在训练阶段：样本数据通过快速正演方法(张志厚等, 2021b)合成，样本数据等效磁异常体通过约束遍历循环获取；利用频率域压制方法(姚长利等, 2003)获取稳定初始模型；将初始模型与任意磁化方向磁异常共同作为FCN网络结构的输入，垂直磁化方向磁异常作为标签进行训练FCN化极网络结构.在预测阶段：将实测数据与频率域压制方法获取的稳定初始模型共同作为输入，直接可以获得最终的预测结果.

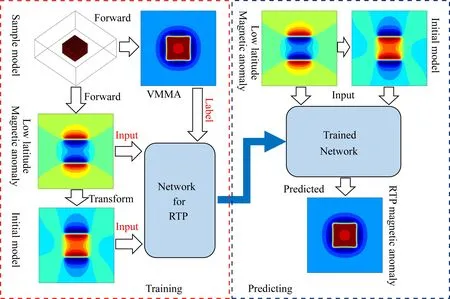
图1 模型约束的磁异常FCN化极流程

1.3 FCN化极网络结构

本文在典型FCN的基础上对其进行简化来作为磁异常化极的网络结构，文中称为RTP-Net，这也是FCN化极方法实现的重要研究内容，FCN化极相当于数据的回归问题，它需要一个稳定的、高分辨率的FCN网络.FCN编解码器网络与传统CNN网络一样是由多个卷积层衔接而成；然而，不同之处在于，编码器-解码器使用卷积层来保留所有空间信息并连接到多维数据，而不是在输出端使用完全连接层来连接分类数据.即，FCN网络结构可以实现任意磁化倾角磁异常数据到垂直磁化磁异常数据的回归，而不是在传统CNN情况下图像数据的分类问题.编解码器的一个重要特征是“瓶颈”架构，输入数据通过编码阶段逐层向下采样，该收缩路径用于获取数据的主要特征信息，然后在解码阶段逐层向上采样，该对称的扩展路径用于精准语义分割.图2为本文FCN化极的网络结构示意图，类似的网络结构在位场边界识别中(张志厚等，2022b)发挥了重要的作用.下采样执行数据的非线性降采样功能，其提取数据的显著信息，如最大池化.相反，上采样采用反卷积算法将数据重构到原始数据维度.传统的FCN下采样容易导致信息丢失，从而致使上采样结果局部信息损失；此外，卷积算子提取局部信息而降低了全局信息的辅助.基于此诸多学者(Badrinarayanan et al., 2017)提出了不同的技术，通过将编码阶段层信息连接到解码阶段对应层来缓解这个问题.文中采用“跳跃连接”技术将编码阶段的层信息复制后融合到解码阶段相应的层.

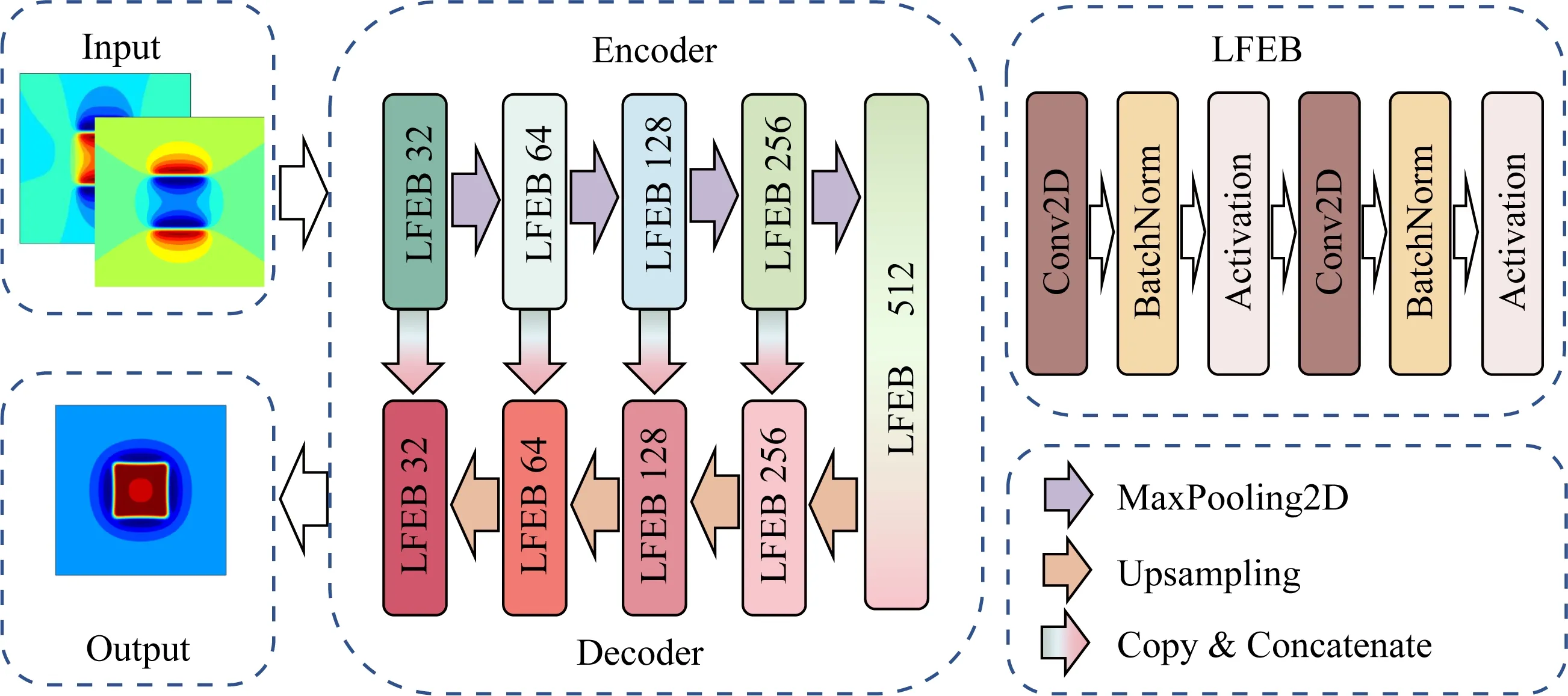
图2 模型约束的磁异常FCN化极网络结构

随着网络深度的增加，编码阶段收缩路径每一个局部特征提取模块(Local Feature Extraction Block, LFEB)的通道数分别为32、64、128、256和512，解码阶段扩展路径LFEB的通道数依次为512、256、128、64和32.每个LFEB包含了双卷积层，并在每个卷积之后进行批处理归一化层(Batch Norm, BN)和非线性激活层，二维卷积的表达式为：

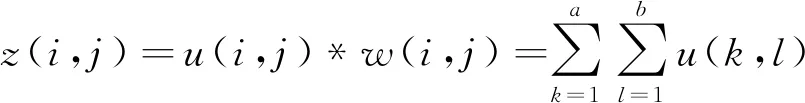
*w(i-k,j-l)，

(12)

式中，u为输入，卷积核w大小为a×b，z为输出.BN有助于稳定训练和防止梯度爆炸，BN的表达式为：

(13)

其中，E[u]与D[u]分别为输入变量u的数学期望和方差，∈是很小的正数，α是尺度因子，β是平移因子.激活函数采用ReLU函数，其表达式为：

ReLU(u)=max(u,0).

(14)

LFEB的输出作为最大池化层或者上采样层的输入，池化或上采样的输出又作为LFEB的输入.最后通过单通道卷积与sigmoid(Badrinarayanan et al., 2017)激活函数进行输出.网络的主体与经典的U-Net相似，网络中总共使用了19个卷积层.

1.4 优化算法

文中RTP-Net的优化即目标函数的极小化过程，采用自适应阶估计(Adam)(Kingma and Ba, 2017)优化计算.参数更新用等式(15)—(20)所示：

(15)

mt=β1mt-1+(1-β1)gt，

(16)

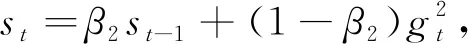
(17)

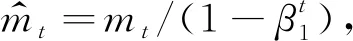
(18)

(19)

(20)

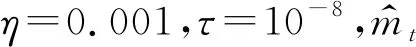
1.5 数据集的构建

数据集的有限性是数据驱动类方法的一大挑战，在精准勘探地球物理时代，大数据集的足量性、典型性与代表性需求显现的极为重要.FCN样本数据集可以是真实数据或仿真数据.针对监督类训练任务，真实样本数据必须提供准确的语义标注.然而，人工标注真实样本数据是一项具有挑战性且非常耗时的工作，并不能满足地球物理数据处理的要求(张志厚等，2022a).通过仿真模拟可以解决数据量大的需求问题，以此可以提高训练模型的泛化性，类似的数据集创建方法也已普遍应用于地球物理的反演中(Puzyrev, 2019; Puzyrev et al., 2019; Li et al., 2021; Liu et al., 2021b; Zhang et al., 2021a; 张志厚等, 2021a, b, 2022a).

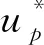
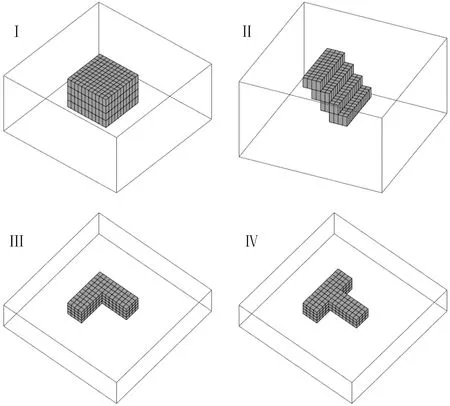
图3 异常体示意图

实际磁异常数据潜在的噪声、采集误差和处理误差将会给化极结果带来了更多的不确定性.为了加强RTP-Net的泛化性能，本文对数据集中10%的随机样本对加入了5%的高斯噪声，以此来增加RTP-Net网络结构的化极效果.与此类似的样本数据构建技术在石油地震(Zhang et al., 2021a)与面波反演(Puzyrev et al., 2019)中取得了较好的应用效果.

图4所示为训练集数据随监督学习轮数的增加目标函数L*(θ)的迅速衰减变化(训练批次大小为1024).可以看出，无论是误差均值的衰减、以及误差最大最小值的变化，还是大部分数据的误差分布规律的变化都表明模型训练良好.

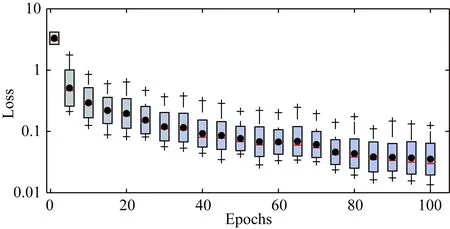
图4 训练数据误差箱线图

1.6 化极效果评估方法

为了定量评价本文所提化极方法的效果，采用决定系数(Barrett, 1974)的大小进行评估.决定系数相比均方误差能够更加直观直接判定结果的好坏，接近1代表效果越好，且不受不同数据量纲差异的影响.决定系数的表达式为：

(21)

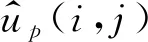
2 模型检验

2.1 单一模型检验

文中采用Hansen和Pawlowski(1989)提出的模型对本文的方法进行检验，该模型为一个20 m×20 m×2 m的棱柱体，顶面埋深为1 m，计算网格点数为64×64，计算点距为1 m×1 m，模型中心点水平方向坐标为(31 m, 31 m).此模型被普遍应用于各种化极方法(Mendonça and Silva, 1993; Keating and Zerbo, 1996; Li and Oldenburg, 2001; 姚长利等, 2003; 骆遥和薛典军, 2009, 2010; 彭利丽等, 2010; 姚长利等, 2012; 骆遥, 2013; Li et al., 2014; 荆磊等, 2017)的效果对比研究.图5a、b分别为水平磁化(I0=0°)和垂直磁化(I0=90°)条件下的磁异常，通过压制因子法获得初始模型如图5c所示.无噪声数据训练集与包含噪声数据训练集的不同网络结构化极结果如图5d—i所示，对比理论磁异常可以得出：(1)在形态上，不同FCN化极方法都获得了较好的结果；(2)磁异常FCN化极结果(图5d)相比初始模型FCN化极结果(图5e)和“初始模型&磁异常”联合驱动的FCN化极结果(图5f)稍差；(3)初始模型FCN化极结果(图5e、h)与“初始模型&磁异常数据”DL化极结果(图5f、i)较为接近，通过决定系数可认为联合驱动FCN化极结果略优；(4)通过决定系数R可以看出，同一方法包含噪声样本数据集训练的网络化极结果(图5g、h、i)相比无噪声样本数据集训练的网络化极结果(图5d、e、f)更好，表明样本数据中加入一定量的噪声样本数据可以增加FCN网络结构的鲁棒性.

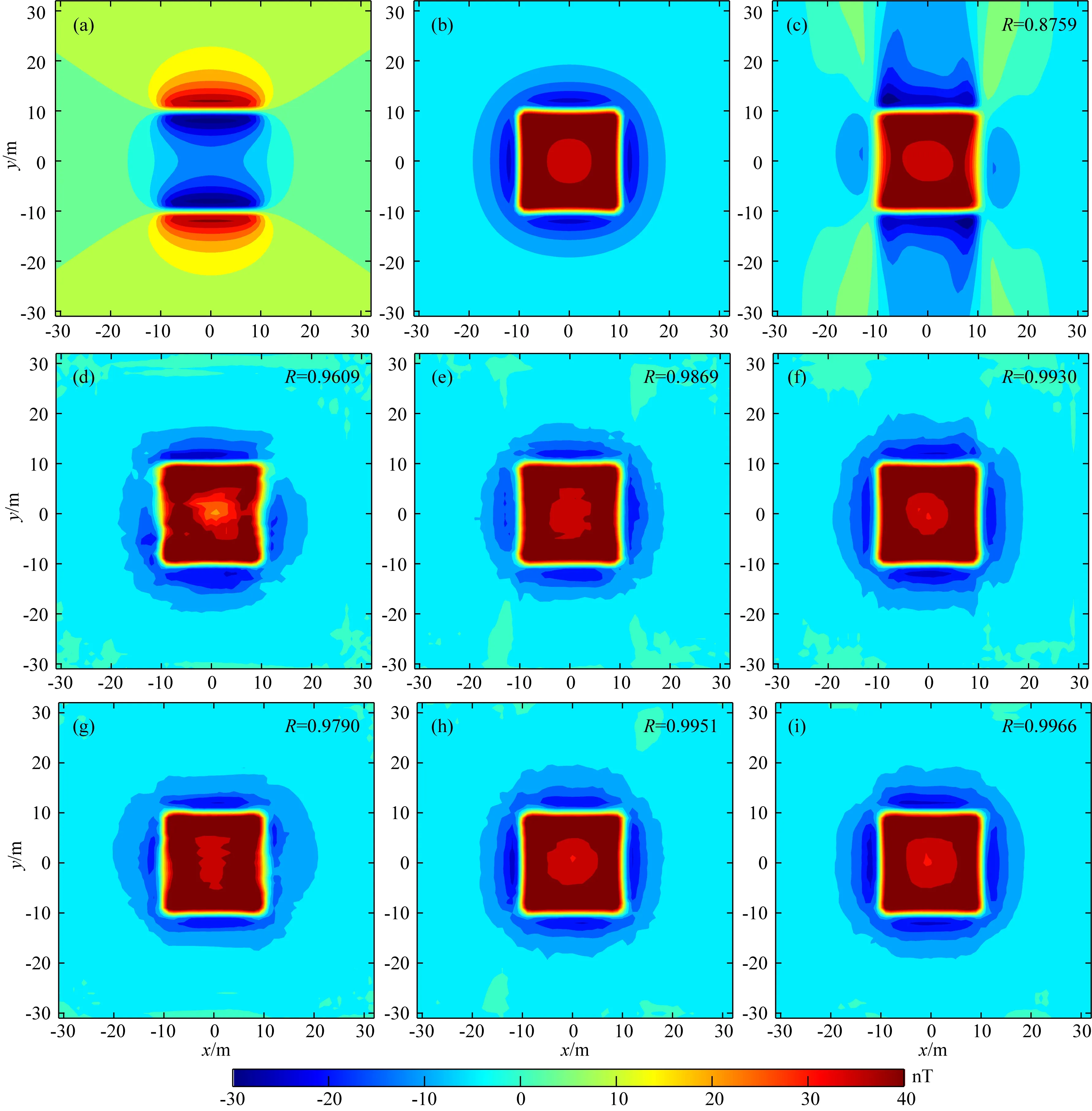
图5 理论模型磁异常化极结果

为了进一步评估化极结果的细节信息，文中抽取了与磁偏角相同方向、且在磁异常体边缘位置的3条剖面(图6).可以看出：(1)在精度上，通过压制因子法获得的初始模型在磁异常形态上与理论异常较为接近，但在磁异常体边缘位置处的计算结果(图6a、b、d、e)相比其他方法的结果较差，初始模型驱动与“初始模型&磁异常”联合驱动方法的精度较高，这两种方法的结果(青色与蓝色曲线)能够接近真实数据；(2)在稳定性方面，纯数据驱动方法(FCN-Magnetic anomalies)化极结果相比其他方法(FCN-Initial，FCN-Initial-Magnetic anomalies)化极结果较差，其包含了较多的随机噪声；(3)含噪声样本训练FCN结果(图6d、e、f)相比无噪声样本训练FCN结果(图6a、b、c)的精度更高.

1.1.1 试剂。党参总皂苷，自制；Cremophor EL40，德国BASF；PEG400，西安天正药用辅料有限公司；橄榄油，江西省吉水中南天然香料油厂；辛酸癸酸甘油三酯，武汉远成共创科技有限公司；Tween-80、Span-80、1,2-丙二醇、甲醇，江苏省海安石油化工厂；人参皂苷Re标准品，中国食品药品检定研究院；香草醛，西安拉维亚生物科技有限公司；高氯酸，天津市鑫源化工有限公司。

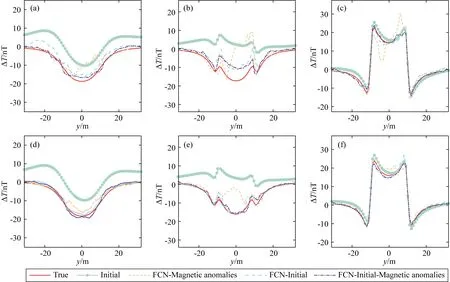
图6 磁异常化极剖面对比图

2.2 组合模型检验

组合模型为四层台阶与两个长方体的组合模型，如图7a所示，台阶模型的每一层大小都为7 m×14 m×1 m，第一层台阶的中心坐标为(48.5 m，26 m，1.5 m)，随着台阶深度每依次递增1 m，其在x方向向小坐标方向平移2 m，依次递增3次，共四层；两个长方体的地面埋深都为1 m，中心点坐标分别为(27 m，42 m，3 m)与(15 m，27 m，3 m)，组合模型的剩余磁化强度都为0.1 A·m-1，磁化偏角都为0°，分别计算了其水平方向(磁化倾角0°)与垂直方向(磁化倾角90°)的磁异常(图7b、c).

通过包含噪声样本数据集训练的DL网络对无噪声理论数据(图7b)以及不同信噪比(Signal to Noise Ratio, SNR)(图8a)磁异常数据进行初始模型频率域转换以及化极运算，结果如图8b、c、d、e所示.可以得到以下认识：(1)采用单一磁性异常体构建的样本数据集对FCN网络进行监督学习，获得的FCN网络可以对组合磁性体的磁异常进行化极，验证了卷积神经网络卷积算子所具有的权值共享性、平移等效性(Bronstein et al., 2017)优势，增加了样本数据场景外的通用性；(2)从结果异常形态上看，除去初始模型存在于磁化偏角平行的狭长条带干扰(图8b，SNR=20、10)，其余都与理论磁异常具有较好一致性；(3)FCN-Initial方法仅以初始模型作为FCN网络结构的输入，其消除了与磁化偏角平行的条带干扰(图8d)；(4)采用包含噪声的样本数据集对FCN网络进行训练，对噪声具有一定的抑制作用，如图8c(SNR=20、10)相比图8a(SNR=20、10)的椒盐噪声较少；(5)FCN-Initial-Mag方法以“磁异常&初始模型”作为网络结构的输入，其相比FCN-Mag与FCN-Initial方法仅以单一数据作为输入的预测结果精度更高、抑噪能力更强，并且效果明显优于其他几种方法.

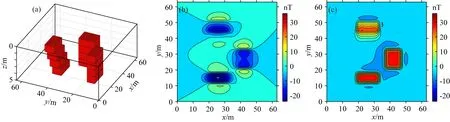
图7 组合模型透视图及磁异常正演结果

为了定量化评估各种方法的化极效果，文中统计了不同方法对不同SNR数据化极的决定系数，如图9所示.可以看出FCN-Initial-Mag方法的化极精度明显优于其他几种方法.另外，包含噪声样本数据训练FCN网络方法的化极结果精度更高(图9b).

2.3 其他维度磁异常化极模型检验

为了检验本文RTP-Net对中高维度磁异常化极效果，文中采用如图7a所示组合模型体进行测试，组合模型体剩余磁化强度为0.1 A·m-1，分别设计两种情况进行检验.第一种情况为磁化倾角为30°、磁化偏角为-2°条件下无噪声(图10a)与含噪声(SNR=20)(图10b)的化极结果，第二种情况为磁化倾角为60°、磁化偏角为-7°条件下无噪声(图11a)与含噪声(SNR=20)(图11b)的化极结果.可以看出，在中高维度情况下，本文所提的RTP-Net也都取得了较好的化极结果，对比各结果的形态与决定系数可以得出：在无噪与含噪两种情况下，“初始模型&磁异常”联合驱动的结果都优于磁异常与初始模型的单一数据源驱动的结果.表明本文所提方法在中高维度也具有一定的通用性.此外，相比低纬度的化极结果(图8)，维度较高区域的磁异常化极结果精度更高.

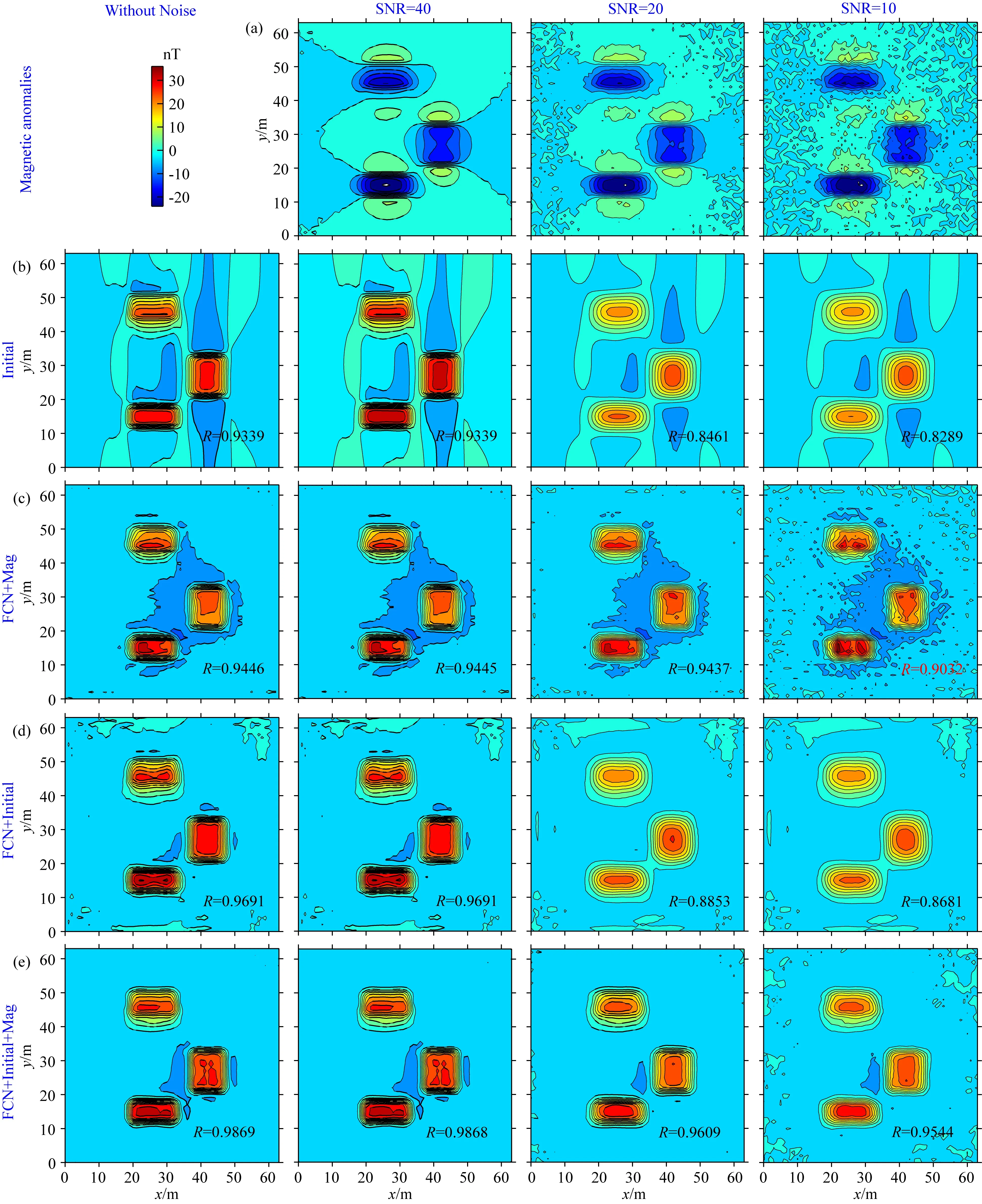
图8 组合模型磁异常及化极结果

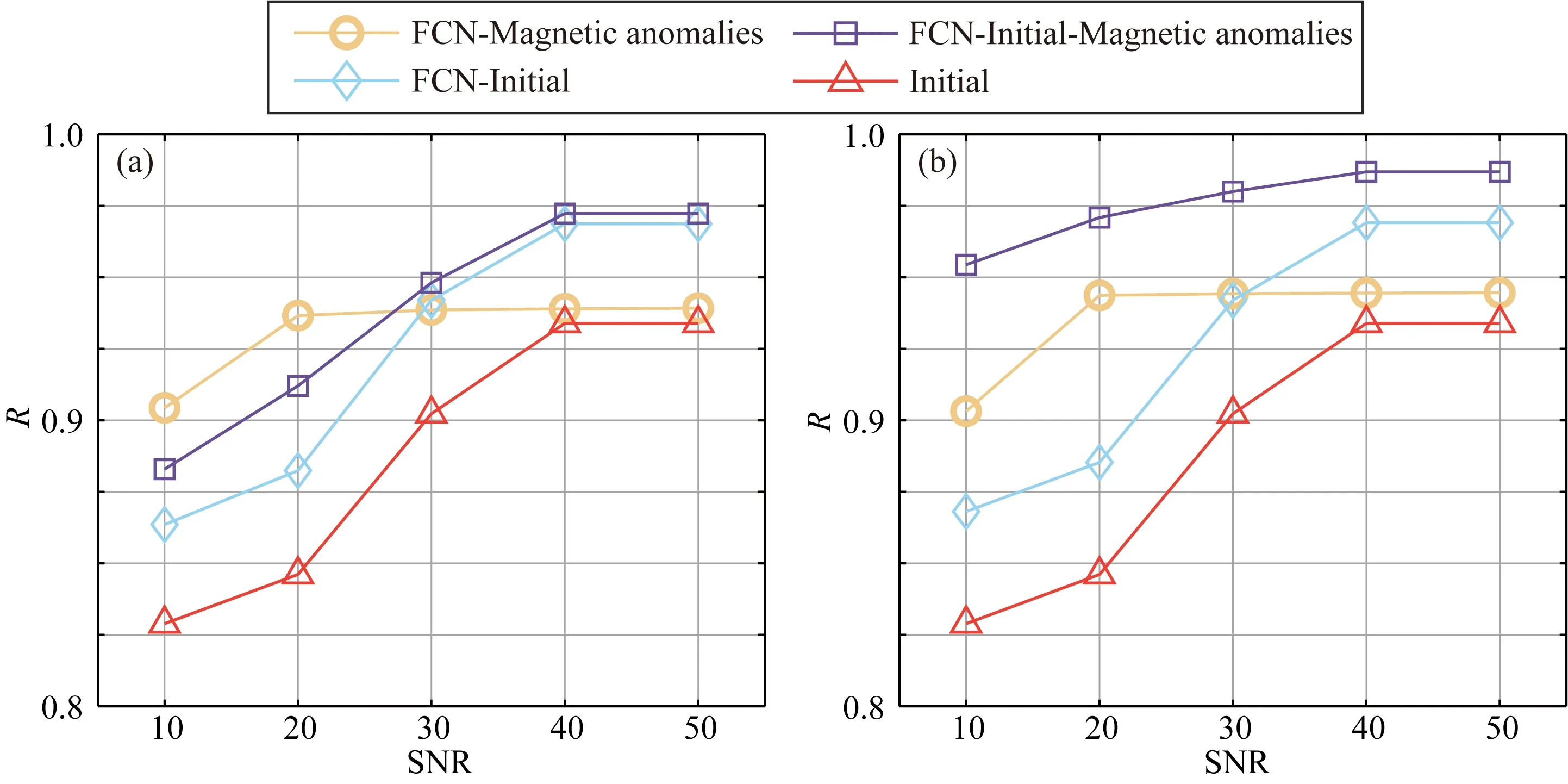
图9 不同方法信噪比的对比

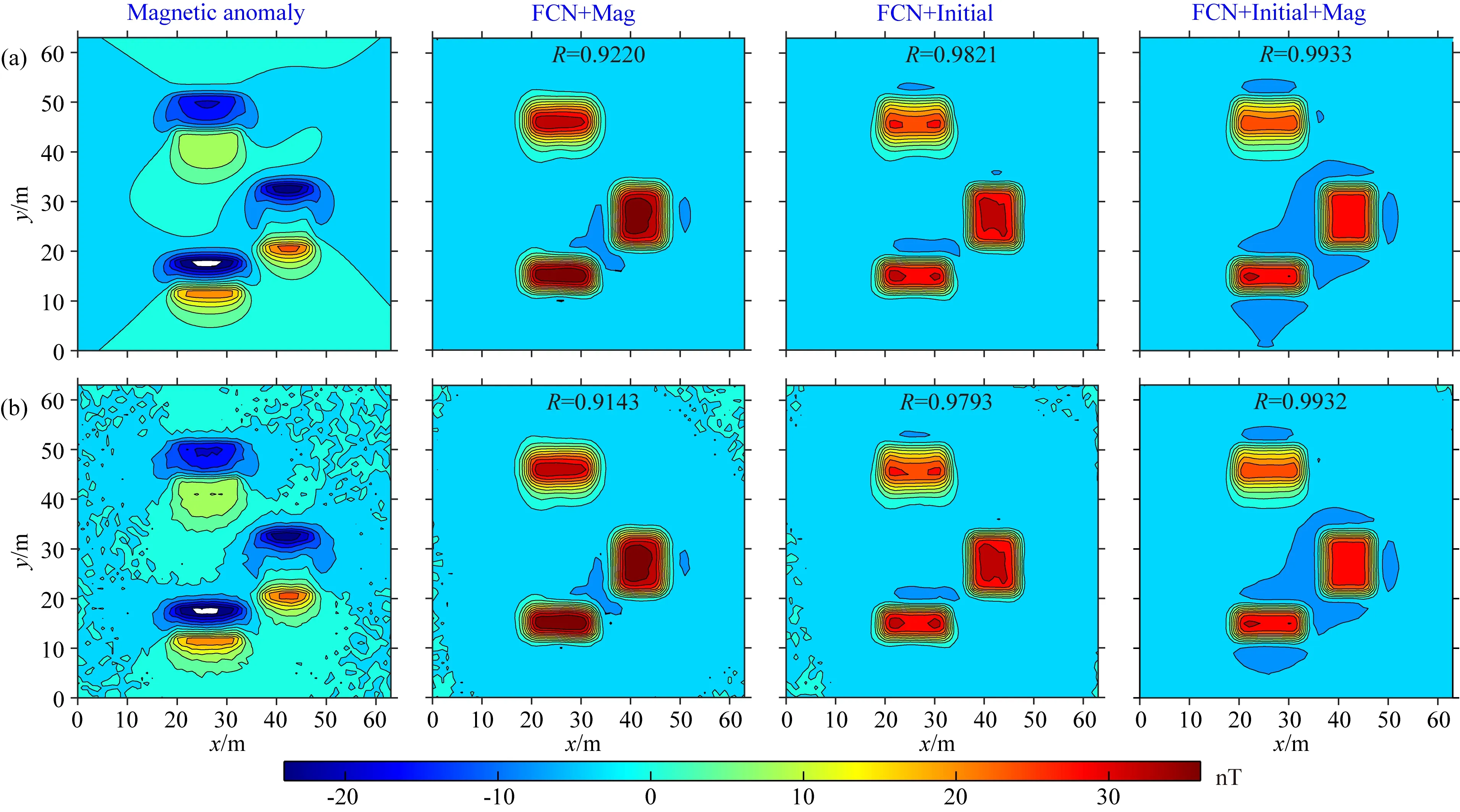
图10 磁化倾角30°情况下组合模型磁异常及化极结果

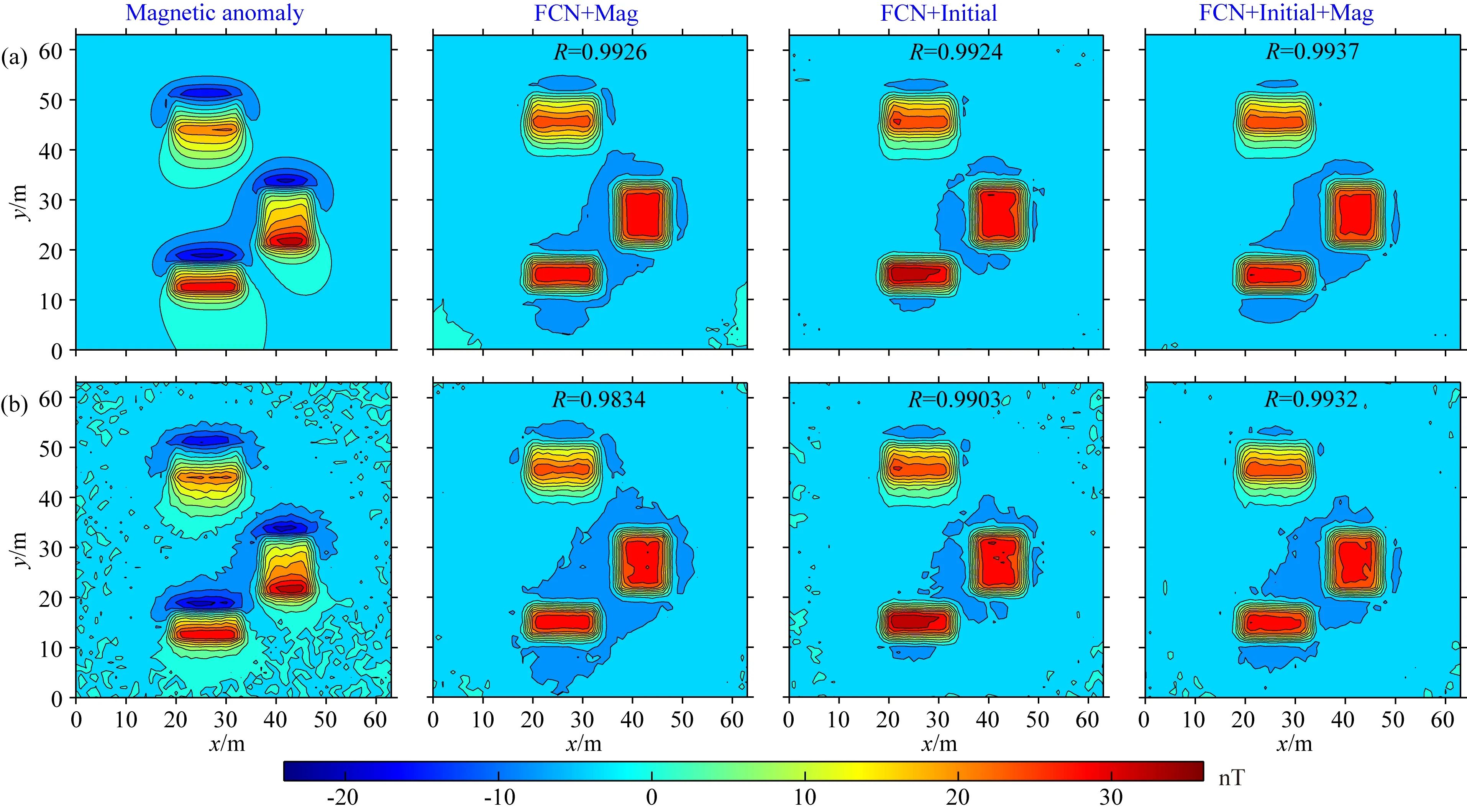
图11 磁化倾角60°情况下组合模型磁异常及化极结果

3 实际案例

采用本文所提方法对东亚某海域的磁测数据进行处理，该区域原始磁测资料点距约为2 km，重新网格化的点距为1.1 km，如图12a所示.测区内的磁化偏角以及磁化倾角均在0°附近，全区选用统一的磁化偏角与倾角分别进行压制因子法与FCN化极处理，结果如图12b、c、d、e所示.对比化极前后的结果，磁异常保持稳定都未畸变，但形态和幅度都发生了较大的变化，但总体而言，FCN方法化极结果(图12c、d、e)与压制因子法化极结果(图12b)较为一致.直接采用磁异常进行FCN化极结果(图12c)形态表现为多个正异常封闭圈，或许该结果有利于进行地质解译.由于东亚海域的特殊性，未能收集到地质或其他地球物理资料进行佐证，但另外两种方法化极结果(图12d、e)与原始磁异常的主要变化为“正、负”异常转换为“负、正”异常，这与文献(方迎尧等, 2006)提出的“倒相”观点更加吻合.“数据&先验信息”联合驱动FCN网络的化极结果(图12e)相比初始模型驱动的化极结果(图12d)能够提供更加丰富的细节信息.

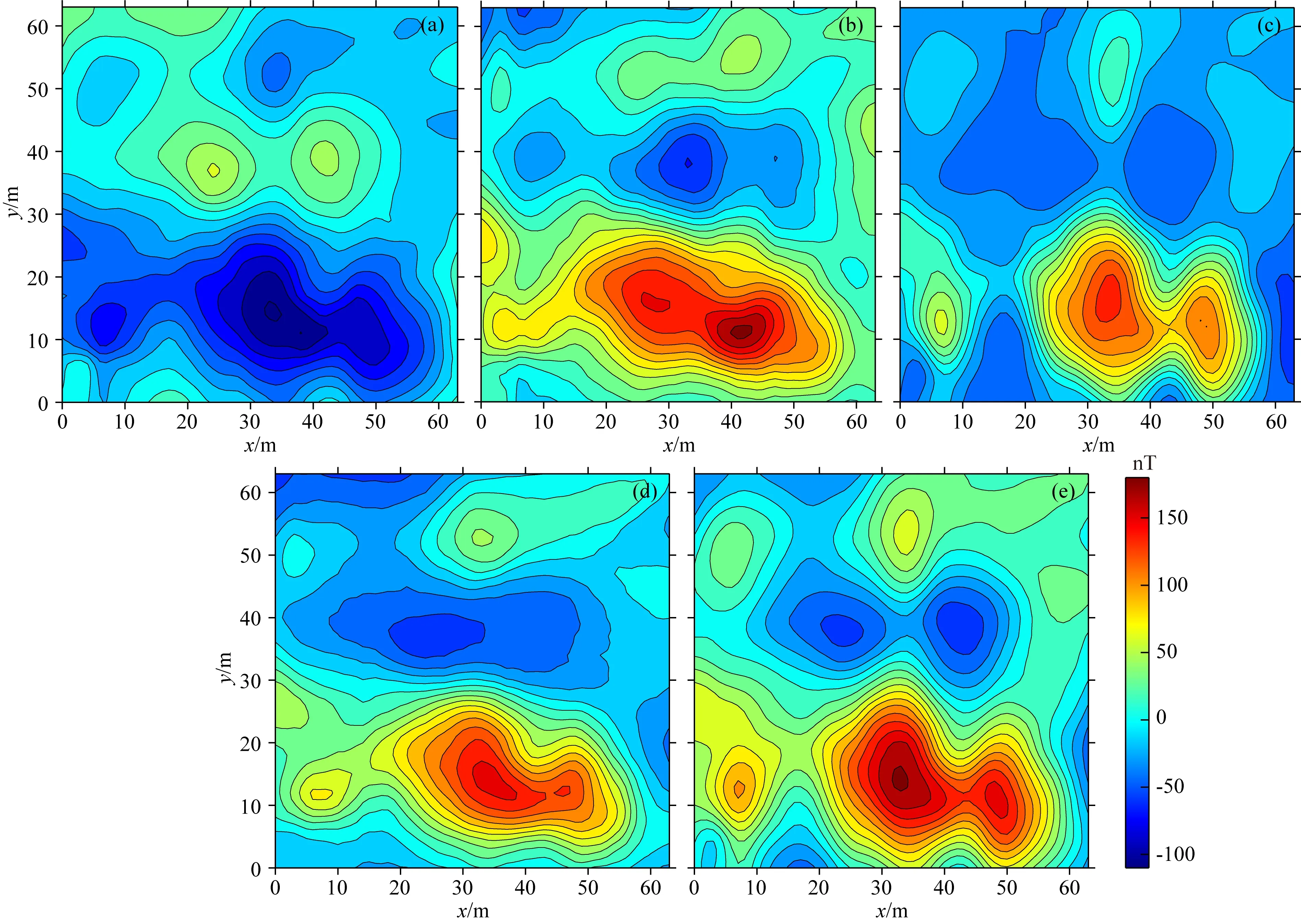
图12 磁异常及其化极结果

为了进一步检验本文方法对其他维度磁异常数据化极的效果，文中对河北保定某区域的航磁数据进行化极，图13a所示为网格化点距为100 m的磁异常数据，该区域的磁化倾角为58°、磁化偏角为-7°.分别采用伪倾角法与本文所提FCN方法化极，结果如图13b、c、d、e所示，可以看出，四种方法化极结果较为相似，且都能很好的将区域中两个范围较大强度较高(均在100 nT以上)的2个异常进行化极，其主要表现一是两个异常形态向北偏移，二是图中左侧的异常基本将正负异常化为正异常体.这两个异常体的展布与区域中北西向、近南北向断裂分布吻合(郭华，2016).另外，2个磁异常体的位置也与目前正在开采的矽卡岩型金属矿有较好的对应关系(郭华，2016).

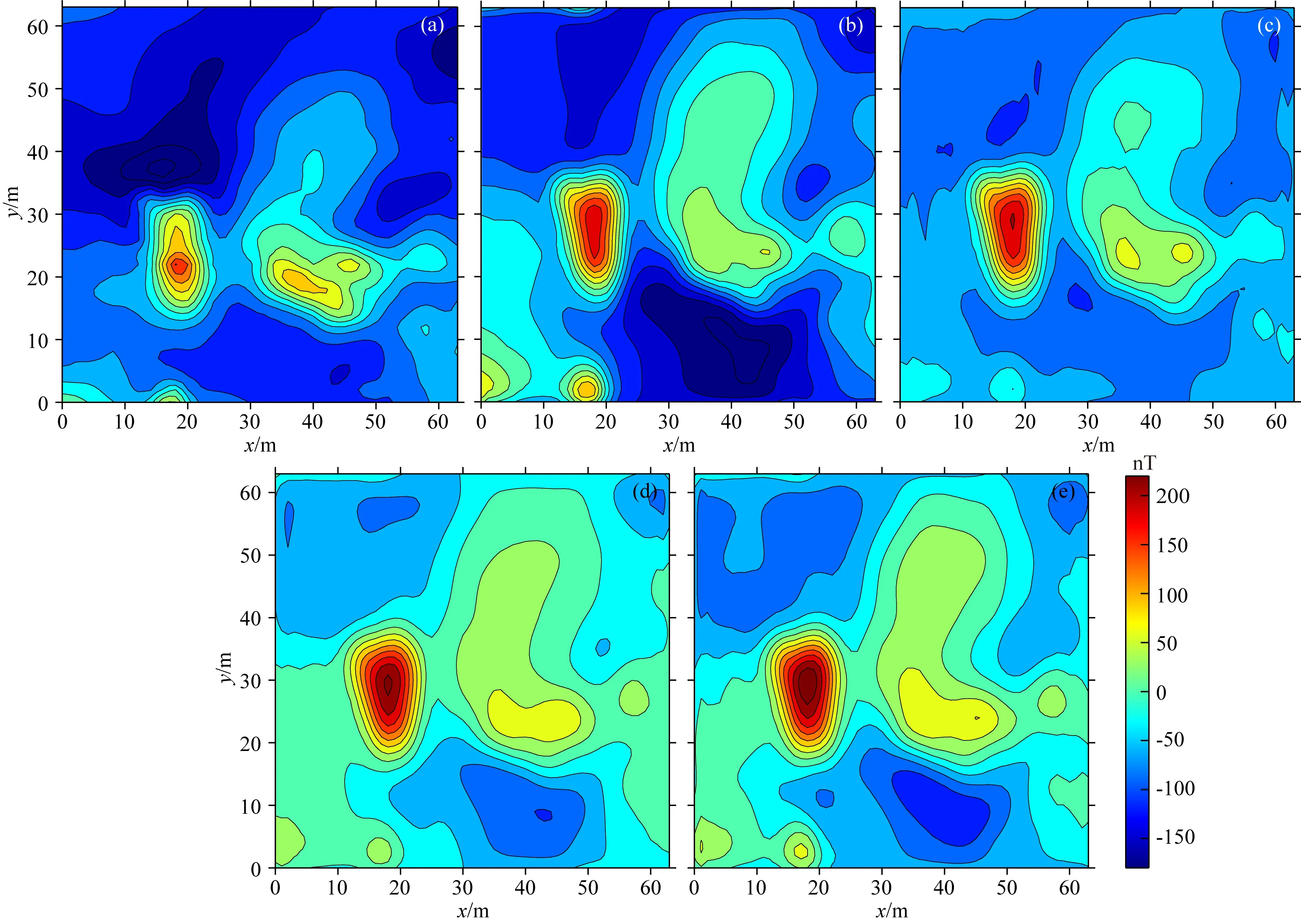
图13 河北某区域磁异常及其化极结果

4 结论与讨论

本文采用了Hansen和Pawlowski(1989)模型与组合模型检验了文中所述方法的效果.综合实验结果表明，联合驱动(FCN-Initial-Magnetic anomalies)方法相比FCN-Magnetic anomalies和FCN-Initial方法可以获得一个稳定、精度更高的垂直磁化磁异常.因此，初始模型有助于提高基于FCN低纬度磁异常化极的泛化能力及精度.中高维度的数据检验也表明文中方法具有一定的通用性.此外，训练样本数据中加入少量含噪声样本可以大大提高FCN网络的鲁棒性.本文所提方法能够实际应用的一个特点是，磁异常化极的低频初始模型可以通过频率域高效稳定的获取，与之相反，传统地球物理线性反演所需的初始模型却难以准确获取.因此，从初始模型获取条件以及准确性角度出发，文中策略还可应用于高精度的位场向下延拓计算.

人工智能崛起势如破竹，深度学习当下风头正劲，其在地球物理领域展现出了强大的能力.然而，这一切在同等计算能力下都需要“数据&算法”做支撑.在数据方面，如何有效地获取小样本数据集，替代遍历循环的大数据集，将是本课题下一步的研究工作，或许随机博弈(Tsiotras, 2021)有望能够改善；在算法方面，文中简化了FCN网络卷积的通道数取得了更为满意的结果，表明奥卡姆剃刀的“如无必要、勿增实体”原理亦然适用于磁异常化极FCN网络结构.因此，需针对不同的具体问题再进行网络结构的搭建或精修，而并非网络结构越深越复杂预测效果越好.除此之外，DL也需要与地球物理特定问题相融，正如本文加入了初始模型的策略才由此进一步增强了FCN化极的效果一样.故而，面对复杂抽象多元的地质地球物理先验知识，如何将其聚沙成塔加入到智能算法中，从而获得少样本条件下的高精度合理解，也值得进一步研究，作者期望未来“知识&数据”联合驱动DL方法也能够推动地球物理数据的高精度处理与解译.

致谢非常感谢匿名审稿专家对论文提出的宝贵修改建议，非常感谢中国地质调查局自然资源航空物探遥感中心郭华研究员、骆遥研究员提供的帮助！