6～50 MHz射频容性耦合Ar等离子体的放电特性

袁强华，秦 彪，殷桂琴，刘朝晖

(西北师范大学 物理与电子工程学院，甘肃 兰州 730070)

容性耦合等离子体源与其他等离子体源相比具有腔室结构简单、能产生大面积均匀等离子体的优点.容性耦合等离子体广泛应用于刻蚀、薄膜沉积、溅射和材料表面改性[1-2].容性耦合等离子体涉及一系列相对复杂的物理和技术过程，放电参数和功率匹配对容性耦合等离子体放电至关重要.研究不同放电参数下等离子体的特性可以更好地调节放电状态，进而提高工艺效率和效果.近年来，放电参数对容性耦合放电等离子体特性的影响仍是一个有意义的研究课题.很多团队利用Langmuir探针、发射光谱和PIC/MCC模拟研究了低温低气压容性耦合等离子体的特性[3-9].

Sarveshwar等[10]利用PIC/MCC方法研究了单频低气压容性耦合等离子体器件在不同射频电压和驱动频率下的动力学特性.他们的研究表明，通过控制驱动频率和施加电压，能够独立控制放电中离子的能量和密度，从而可以有效地应用于等离子体处理领域.Kikuchi等[11]研究了恒定电压和气压条件下的容性耦合放电中驱动频率对等离子体密度的影响，结果表明，80～500 MHz的等离子体密度与驱动频率成正比.Bhattacharjee等[12]利用PIC模拟研究了激发频率对低频放电中电子能量分布函数的影响.Colgan等[13]研究了低气压(250 mTorr)容性耦合氩气放电中频率变化对等离子体的影响，给出了空间分辨光发射和射频电压电流的测量结果.Schuengel等[14]利用PIC/MCC模拟研究了放电参数变化对低气压容性耦合氩等离子体的等离子体密度和电子动力学的影响.Abdel-fattah等[15]研究了在固定射频电压(50～130 V)和固定氩气气压为100 mTorr条件下，13.56～60 MHz激发频率对电子能量分布函数的影响.

文中采用光谱法和PIC/MCC模拟研究了气体流量为30 mL·min-1、气压为40 mTorr、驱动频率分别为6 MHz、15 MHz、35 MHz和50 MHz时容性耦合氩等离子体的放电特性.首先，在固定气压和驱动频率下，讨论了功率的增加对等离子体放电特性的影响.然后讨论了在功率和气压固定的情况下，驱动频率的增加对等离子体放电特性的影响.

1 实验装置

图1给出了实验装置图.这在我们前期的工作中有详细的介绍[16]，这里作简要叙述.气体在两侧为15 cm的平行方形电极之间放电产生等离子体，电极间距固定在3.2 cm.真空反应系统由一个机械泵和一个分子泵组成.平行电极位于腔室中，腔室长、宽、高分别为23,23,22 cm.腔室采用不锈钢外壳，可屏蔽电磁干扰，它具有良好的阻隔效果，避免了功率电极与室壁之间的等离子体击穿，可以提供稳定的放电环境.上电极与可调射频电源连接，下电极与地面连接，射频功率可调范围为0～300 W.电压波形由高压探头测量，数字示波器采集.在模拟中，测量到的电压波形被用作电位边界.在本实验中，进入腔室的气体流量固定在30 mL·min-1，气体流量由气体质量流量计控制，气体气压由MKS压力传感器调节，可以调节的范围是0～1 Torr.诊断时使用Avaspec-2048-8光谱仪测量等离子体发射光谱，测量波长范围为200～1078 nm，采集的实验光谱传输到计算机进行实时记录.

图1 实验装置图

2 电子温度和电子密度的计算方法

假设在所有选定能级上的各种自由速率粒子遵循麦克斯韦分布，而各激发态能级的布居遵循玻尔兹曼分布.在这种情况下，可以得到电子激发温度.具体过程是将多条谱线对应的谱线信息代入(1)式，其斜率为电子激发温度[17]:

(1)

其中，Iij和λij分别为光谱谱线强度和波长；gi和Ei为统计权重和上能级能量；k为玻尔兹曼常数；C为常数.

然而，在低密度、低气压条件下，要维持等离子体的局部热力学平衡很难.激发态的布居偏离了玻尔兹曼分布，所以用玻尔兹曼方法求得的电子激发温度并不等于电子温度.因此，可以使用一种修正的玻尔兹曼方法来计算等离子体非局部热力学平衡时的电子温度.因此，低气压等离子体符合日冕平衡方程[18-20]

(2)

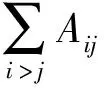
(3)

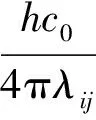
(4)

通过(2)～(4)式的推导，可以得到关于Te的表达式[18,22]

(5)

其中，D为常数；k为玻尔兹曼常数.非局部热力学平衡下的电子温度可由上式求得，拟合后，直线斜率的倒数即为电子温度.文中选取的6条谱线信息如表1所示.

表1 Ar光谱谱线的参数[21-22]

等离子体的电子密度由下式[5,17,23]得到

(6)

其中，上式中的jλ(λ)和gλ(λ,Te)可由(7)～(11)式得到

其中，k为玻尔兹曼常数；Te为电子温度；na为原子密度；ξfb(λ,Tb)和ξfb(λ,Te)比伯曼系数.

3 结果与讨论

图2给出了在功率为10 W、频率为6 MHz时实验测量得到的光谱图.当驱动频率固定在6 MHz时，所选光谱的6条谱线的强度随功率在10～80 W的变化情况如图2b所示.从图中可以看出，随着功率的增加，谱线强度相应增加.这可能是因为随着功率的增加，电子会从电场中获得更多的能量，从而进一步促进碰撞过程，碰撞产生的激发态粒子数量增多，光谱谱线强度增强.

图2 Ar的发射光谱及功率为10～80 W条件下Ar谱线强度的变化

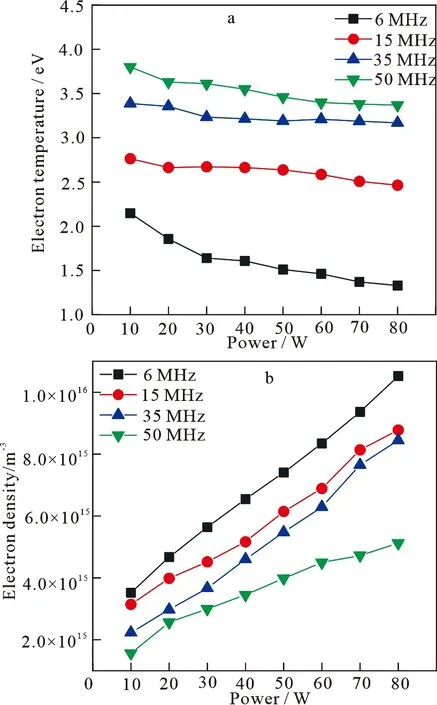
图3给出了固定气压为40 mTorr、射频功率为10～80 W、频率为6、15、35、50 MHz时的电子温度变化情况.随着功率的增大，电子温度由急剧下降到平缓下降，然后趋于稳定.这是由于随着射频功率的增加，电场强度增强.更强的电场使电子在鞘层区域加速，电子获得更多的能量，并由此随之产生更多的高能电子.另外，由于产生了越来越多的电子，特别是高能电子，电子平均自由程减小，所以与中性原子的碰撞就越强烈，能量越高的电子就会失去能量.这样，电子的平均动能逐渐减小，低能电子数逐步上升，高能量电子数逐渐下降，所以功率的升高使电子温度逐步降低[21-25].图3a也明显地展示了电子温度随驱动频率的增加而升高.在恒定功率为60 W的情况下，电子温度在6 MHz时为1.66 eV，在50 MHz时增加到2.74 eV.如图3b所示，在图3a相同条件下，放电中心的电子密度随着功率的增大而升高[26].这是因为随着功率的升高，电子可以获得更多的能量并电离中性气体.电离速率随功率的增加而增加，导致电子密度的增加.激发频率对电子密度的影响如图3b所示，随着频率的增加，电子密度减小.在功率恒定为60 W的情况下，从6 MHz到50 MHz，电子密度从1.36×1016m-3变化到4.68×1015m-3.Ahn等[27]得到了一个显著的结果，随着驱动频率的增加，电子温度升高，电子密度几乎保持不变或降低.这一结果与之前的研究结果相反.这一结果初步解释了在固定功率条件下，等离子体中碰撞加热随驱动频率的增加而增强.

气压为40 mTorr, 射频功率为10～80 W

4 PIC/MCC模拟

表2 反应类型、碰撞过程及其阈值[30]

图4给出了在6,15,35,50 MHz 4个频率下通过PIC/MCC模拟得到的电子温度和电子密度，可以看出，随着功率的增大，电子温度逐渐降低.随着驱动频率的增加，电子温度显著升高[8,31-34].在60 W的恒定功率下，电子温度在6 MHz时为1.46 eV，在50 MHz时为3.39 eV.电子密度如图4b所示，电子密度随功率的升高而升高，随驱动频率的增加而降低.随着频率从6 MHz增加到15 MHz，电子密度从8.34×1015m-3降低到4.49×1015m-3.因此，通过模拟与实验对比发现，模拟结果与实验结果变化趋势较一致.

固定气压为40 mTorr、射频功率为10～80 W

图5给出了不同功率和频率下的电子能量分布函数.在4个频率不同功率下的电子能量分布函数近似双麦克斯韦分布.结果表明，随着功率的增加，低能电子布居数不断增加，而高能电子布居数不断减少，所以电子温度随着功率的增加而降低，这与图4一致.

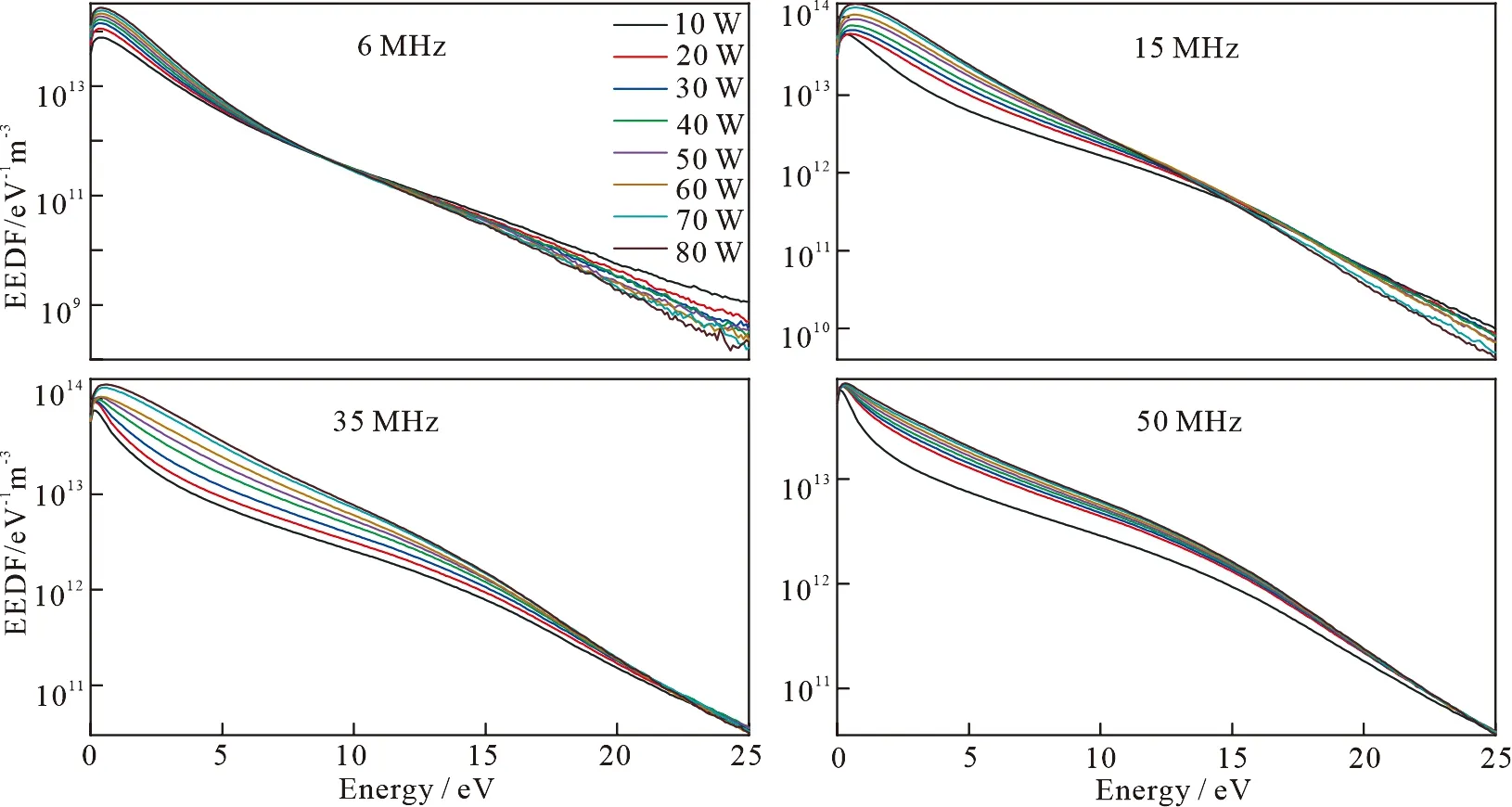
图5 在6～50 MHz的4个驱动频率下，10～80 W功率范围内放电中心的电子能量分布函数

图6给出了恒定功率为60 W时4种频率下的电子能量分布函数.随着频率的增加，高能电子的数量不断增加，而低能电子的数量不断减少.这可能是高能电子随着频率的增加而增加，但高能电子的能量没有达到碰撞的能量阈值，导致高能电子的积累.因此，电子温度升高，电子密度降低[35]，与图4一致.图7为固定频率为6 MHz时，20,40,60和80 W功率下电场强度的时空分布.结果表明，随着功率的增加，鞘层厚度变薄，电场强度增大.鞘层厚度随功率的变化可能是由于电子密度随功率的增大而增大.

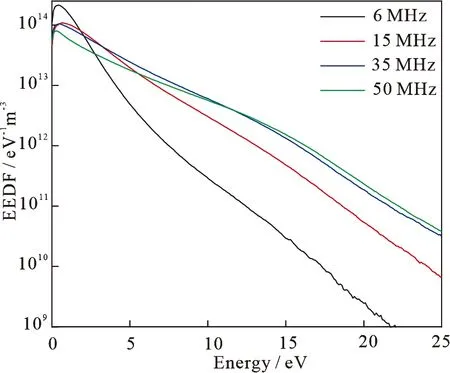
图6 固定功率为60 W时，驱动频率为6,15,35,50 MHz条件下放电中心的电子能量分布函数

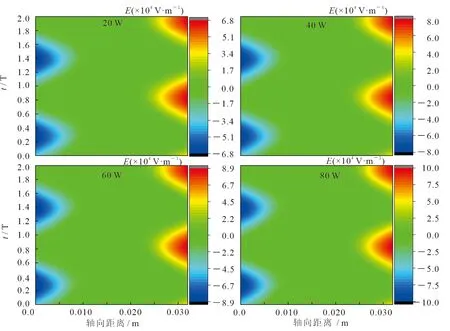
图7 频率为6 MHz，功率为20,40,60和80 W时的电场强度时空分布

图8给出了在功率为60 W时4个频率下的电场强度时空分布.这些结果表明，随着驱动频率的增加，鞘层区域的电场强度减小.频率越高，鞘层厚度越薄.在低气压下，等离子体的加热机制主要是随机加热.随着频率的增加和电场强度的减小，等离子体的随机加热减小，等离子体的边缘效应增大，这也可能是电子密度随驱动频率降低的原因[36-39].

图8 固定功率为60 W时，驱动频率为6，15，35，50 MHz的条件下电场强度的时空分布

5 结论

文中通过实验和PIC/MCC模拟研究了频率为6，15，35和50 MHz时容性耦合氩等离子体的放电特性.结果表明，在固定气压和固定频率条件下，随着功率的增大，电子密度升高，电子温度降低.当功率和气压一定时，随着频率的增加，电子密度降低，电子温度升高.通过PIC/MCC模拟得到的结果和实验比较后发现其变化趋势较一致.从模拟得到的电子能量分布函数可以看出，电子能量分布函数呈双麦克斯韦分布，高能电子布居数随功率的增大而减小，低能电子布居数随功率的增大而增大.当功率恒定为60 W时，高能电子布居数随频率的增加而增加，而低能电子布居数随频率的增加而减少.这可以解释电子温度随频率的增加而增加.通过电场的时空分布可以看出，电场强度随功率的增加而增大，随频率的增加而减小，鞘层厚度随功率和频率的增加而减小.