基于深度学习的波长调制吸收光谱非线性层析重建研究

王振海，超 星

(清华大学能源与动力工程系燃烧能源中心，北京 100084)

可调谐二极管激光吸收光谱(tunable diode laser absorption spectroscopy，TDLAS)技术作为一种新型的非接触式测量手段，利用H2O、CO、CO2等分子的特征吸收谱线，可以实现温度、组分浓度、压力等气体物性参数的测量[1-4].与传统接触式测量方法相比，TDLAS 技术具有灵敏度高、响应速度快、原位测量等显著优势，目前已经广泛应用于大气环保、能源电力、航空航天等领域.激光吸收光谱技术主要分为两种测量实现方法：直接吸收法(direct absorption spectroscopy，DAS)和波长调制法(wavelength modulation spectroscopy，WMS)，其中，波长调制法通过对激光器进行高频调制，对实际环境噪声具有较强的免疫性，且可通过谐波信号归一化实现免标定原位测量，典型的吸光度检测下限约为10-4量级，灵敏度约为直接吸收法检测下限的10 倍[5].

TDLAS 技术仅能给出单一测量路径上的积分平均值，测量不具备空间分辨率，无法反映流场内部因化学反应、相变热交换等过程所引起的温度及组分浓度场不均匀分布.针对这一问题，目前在燃烧诊断领域，已有大量基于吸收光谱技术的多维光学诊断理论算法和实验测量研究相继开展[6-7].针对流场的非均匀分布，目前围绕TDLAS 开展的光学测量研究可分为3 个方面：①采用宽光谱光源，利用多条吸收谱线，同时结合数值模拟研究等其他方法，获取沿路径方向的温度及组分浓度不均匀分布[8-10].如Sanders等[8]利用760 nm 附近的16 条吸收谱线，实现路径上两段式温度分布的测量.②将TDLAS 技术与计算机层析成像技术(computed tomography，CT)相结合，利用反演算法进行燃烧流场的二维重建研究[6-7].如Kasyutich 等[11]通过采集5 个角度共55 条投影光线数据，实现二维温度分布测量.③利用高速红外相机，搭建吸收光谱成像系统，以Spearrin 等将中红外相机用于射流火焰中多参数(如温度、CO 和CO2浓度)测量为代表[12-13].本文主要围绕计算机层析吸收光谱技术在非均匀燃烧场的二维重建研究展开.

计算机层析吸收光谱技术，本质上为求解反问题，根据反问题性质不同，可以分为线性层析和非线性层析吸收光谱技术[6].线性层析吸收光谱技术通常选用两条吸收谱线，需要多角度布置多条光线，实验成本较高，反演重建算法主要分为两类：以Radon 变换为基础的滤波反投影算法、Abel 变换等和以级数展开法为基础的代数迭代法、最大似然估计法等，上述算法对投影光线的数目、布置方式要求苛刻，且在层析信息矩阵秩亏情形下，重建精度、鲁棒性和计算效率均有待进一步提升，限制了高精度、实时性的二维重建测量在实际燃烧环境中的应用.非线性层析吸收光谱技术通常选用两条以上吸收谱线，利用超光谱光源或频分复用等技术，可以利用单一路径上几十或几百条吸收谱线同时进行温度或组分浓度分布重建，该方法可通过增加吸收谱线的数目从而减少层析成像光路布置中所需要的投影光线数目，进而降低系统复杂度[14-17].Ma 等[14]提出超光谱非线性层析技术，采用傅里叶域锁模光纤激光器，将其用于实际航空发动机J85 尾喷口气流的高时空分辨率测量.

然而，上述线性或非线性层析重建中多采用直接吸收光谱法，信号处理简单，但在实际燃烧环境中应用往往面临信噪比低、基线拟合误差大、高压谱线展宽等问题.2014 年，Cai 等[16]通过频分复用技术，设计基于免标定波长调制光谱技术的非线性层析成像方案.该研究利用5 条吸收谱线，2 个投影角度共计30 条投影光线，结合模拟退火算法，实现温度、浓度二维分布重建.近年来，深度学习技术发展迅速，已广泛应用于计算机视觉领域(如图像分类、目标检测、图像恢复等)任务，这为解决层析重建的病态反问题提供了一种新的解决思路.Jiang 等[18]在研究基于直接吸收光谱法的线性层析问题中，将卷积神经网络用于双通道即温度、浓度二维重建研究，并首次开展了基于深度学习的计算机层析吸收光谱实验验证.Deng 等[19]在研究基于直接吸收光谱法的非线性层析问题中，将深度学习用于反问题研究中，比较了卷积神经网络(convolutional neural network，CNN)、深度信念网络(deep brief network，DBN)、循环神经网络(recurrent neural network，RNN)的二维温度重建结果.在上述相关工作的基础上，本文基于深度学习算法，开展了免标定波长调制吸收光谱非线性层析重建研究，从算法理论层面实现了二维温度、浓度重建，为下一步非线性层析重建实验的开展提供指导.

1 非线性层析重建技术研究

1.1 波长调制吸收光谱技术

半导体激光器在低频扫描和高频调制信号的共同作用下，其输出特性为

式中：I0为激光器平均强度；im,k为激光器强度在高频信号作用下的调制幅度，通常有 im,1≫ im,k＞1；φm,k为激光器在高频信号作用下强度输出和频率输出的相位差.

根据比尔-朗伯定律，频率为v 的单色激光通过气体吸收介质后，光强透射率表达式为

式中：τ(v)为透射率；α(v)为吸光度；T(x)、X(x)分别为测量路径上的温度和组分分布；S[T(x)]为与温度有关的吸收谱线线强；p 为待测区域总压，φ(v -v0)为吸收谱线线型函数.

将透射率τ(v)按照傅里叶余弦级数形式展开：

式中：Hk(v，a)为k 次谐波的傅里叶分量，则有

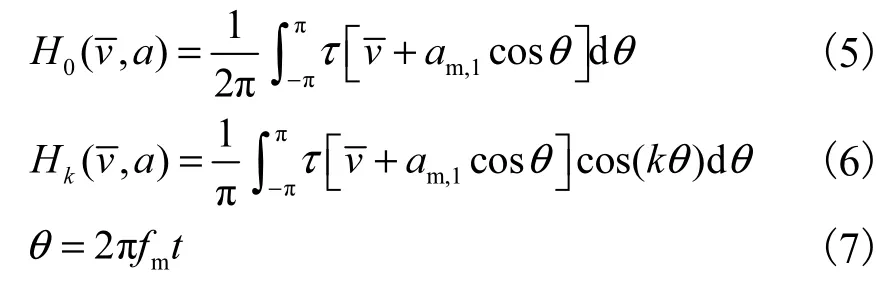
式中：激光器透射光强It(t)可以表示为

式中G 为光电探测器增益.利用锁相放大技术提取透射光强信号It(t)在nfm处频率分量，即n 次谐波信号，可以表示为

式中：LPF(t)为低通滤波器脉冲响应函数；*表示卷积运算；j 为虚数单位.

取激光器前两阶光强调制项，即im,k＞2＝0，则一次和二次谐波信号分别为

用1 f 信号将2 f 信号归一化，可消除光电探测器增益G 和光强的影响，同时可以抑制激光器、探测器的共模噪声，归一化后的信号为

1.2 非线性层析重建

图1 所示为本文所采用的非线性层析重建光路布置示意图，与采用超宽光谱进行非线性层析吸收光谱研究不同，本文参考Cai 等[16]的工作，选用L 支窄带宽半导体激光器，对L 支激光器进行频分复用，即以不同调制频率fm,1，fm,2，…，fm,L进行高频调制.待测区域边长为N，将其离散划分为n×n 的网格单元，激光投影角度数为s，通常可取0°、45°、90°和135°等角度布置，每个角度投影数为q，总投影路径数为 M＝s×q.

图1 非线性层析重建光路布置示意Fig.1 Schematic diagram of nonlinear multiplex absorption tomography

由M 个光电探测器接收不同投影方向的透射光强信号，通过锁相放大技术，提取中心谱线位置处的归一化2 f/1 f 信号，最终得到的L 条吸收谱线在M条投影路径对应的归一化2 f/1 f 信号矩阵为

1.3 深度学习算法

卷积神经网络通常包括输入层、卷积层、池化层、全连接层及输出层.在本文中，输入层为中心谱线位置处的归一化2 f/1 f 信号投影矩阵(S2f/1f)v0，维度为L×M，卷积层可以进一步提取输入矩阵特征，起滤波器作用，其运算过程为

式中：X为输入矩阵；Y为输出矩阵；W为卷积核权重矩阵；b为偏置系数矩阵；g 为卷积层所采用的激活函数.本文采用的激活函数为ReLU(rectified linear units)函数，该激活函数率先从根本上解决梯度消失和梯度爆炸等问题.池化层起降采样作用，剔除特征图中不重要样本，避免过拟合，提高模型泛化能力，包括最大池化、平均池化等.通过全连接层，可将多维特征矩阵转化为一维向量，通过分类或回归函数实现输出.

卷积神经网络的训练过程主要分为两部分，第1部分是前向传播阶段，前向传播的主要作用为将输入的特征信息进行前向传递，预测值与真实值之间的误差值可用损失函数进行表示，以温度场二维重建的均方根误差(root square mean error，RSME)为例：

式中：BS为批块大小；为第i 个批块中第j 个网格温度的真实值；为第i 个批块中第j 个网格温度的重建值.

第2 部分为反向传播阶段，计算损失函数关于参数的梯度，将损失函数由输出层传递至隐藏层，再传递至输入层，通常选择Adam(adaptive moment estimation)算法进行参数优化，根据参数梯度的一阶矩和二阶矩自动选择参数学习率，改善稀疏梯度.输出层为温度和组分浓度的二维分布，定义一阶矩误差，以评估二维温度、浓度分布重建精度，可以表示为

式中：eT和eX分别为二维温度、浓度分布重建误差；Tground和Xground对应真实的二维温度、浓度分布矩阵；Trecons和Xrecons对应重建的二维温度、浓度分布 矩阵.

2 非线性层析重建方案设计

2.1 层析吸收光谱方案设计

以H2O 分子温度和浓度重建测量为例，为便于光路布置，采用近红外波段较为成熟的半导体光纤激光器.选择5 条吸收谱线，中心波数分别为v0,1＝7 294.13 cm-1、v0,2＝ 7 306.75 cm-1、v0,3＝ 7 339.83 cm-1、v0,4＝ 7 416.05 cm-1和 v0,5＝7 444.37 cm-1，相关光谱参数可在HITEMP 2010 光谱数据库[20]中查找.

图2 所示为近红外波段H2O 分子吸收谱线(7 444.37 cm-1)在不同温度、浓度下的吸收情况示意图，其中图2(a)为吸光度信号，幅值约为10-4量级，此时在实际燃烧环境测量中采用波长调制法更有优势，图2(b)为波长调制法中，一定激光器调制参数下 S2f/1f信号示意图，其中，中心谱线位置即虚线处S2f/1f值最大，该位置处信噪比最高，图2(c)为不同温度情况下S2f/1f信号变化，呈非线性递减趋势，图2(d)为不同浓度情况下S2f/1f信号变化，呈非线性递增趋势.由图2(c)和(d)可知，S2f/1f与温度、浓度之间的非线性耦合关系，将为吸收光谱层析重建带来较大的困难.

图2 近红外波段H2O 分子谱线(v0,5＝7 444.37 cm-1)在不同温度、浓度下的吸收情况Fig.2 Simulated absorbance and S2f/1f profiles for H2O transition(v0,5＝7 444.37 cm-1) with different temperature and H2O concentration

对每个激光器进行高频调制，通过多路复用器将5 路激光器耦合至同一光纤，然后经过分束器和准直器，穿过待测区域，由光电探测器接收信号.本文设定的待测区域为边长N＝50 cm 的方形区域，网格单元数为d＝21，激光投影角度数为s＝2，即采用0°和90°角度布置，每个角度投影光线数为p＝10，总投影光线数为M＝20.相比于传统线性层析吸收光谱技术，采用频分复用的非线性层析吸收光谱技术可以大大简化实验光路布置，减少总投影光线数目.

实验仿真验证中采用的火焰场为两个不同位置、不同形状的二维高斯温度、浓度分布场的叠加，用以模拟实际燃烧中火焰的非对称性，具体地，火焰场二维温度、浓度分布可以表示为

式中：f(x，y)为二维温度或浓度分布；ai为两个高斯分布的随机权重系数，范围为0～1，G(xi，yi，μi，σi)为二维高斯分布函数；μi和σi分别为高斯分布所对应的均值和方差，在生成二维温度和浓度分布时，均值和方差均在一定区间内随机取值.本文中二维高斯分布峰值温度区间为750～2 200 K，峰值浓度区间为0.01～0.05，均值区间为3～18，方差区间为2～7.图3(a)和(b)分别为仿真得到的典型二维温度、浓度分布，图3(c)为5 条吸收谱线在20 条投影路径上的S2f/1f信号值，可见，S2f/1f信号分布与温度、浓度分布有明显的特征对应关系，进一步证明了后续采取卷积神经网络进行深度特征提取的可行性.

图3 本文仿真得到的典型二维温度、浓度分布以及5 条吸收谱线在20条投影路径上的S2f/1f 信号Fig.3 Representative distributions of temperature and H2O concentration，and the corresponding S2f/1f signal

2.2 卷积神经网络设计

图4 为本文设计的卷积神经网络结构示意图，包括输入层、卷积层、池化层、全连接层及输出层.其中，C1、C2、C3、C4 为卷积层，S 为下采样层，FC 为全连接层，实验得到20 个探测器在5 条吸收谱线中心位置处的S2f/1f值，即5 条吸收谱线在2 个投影角度，10 条投影路径下的值，为5×2×10 的输入矩阵，经过卷积层和池化层，到达全连接层，全连接层为441×1，对应441 个网格节点，经过回归分析，可得整个待测区域内的二维温度或组分浓度分布.整个深度卷积神经网络模型的参数，包括卷积核大小、每层神经元数目都展示在图4 中.

图4 卷积神经网络设计示意Fig.4 Schematic diagram of convolutional neural network in this work，convolutional layers

3 结果与讨论

3.1 卷积神经网络参数优化

利用给定的二维温度、浓度分布，可以计算得到对应的归一化2 f/1 f 信号投影矩阵，本文总仿真样本数目为10 000，其中95%用于训练卷积神经网络，5%作为测试集.神经网络训练平台配置参数如下：处理器为Core i9-10900 K CPU(3.7 GHz)，32 GB RAM，显卡为NVIDIA GeForce GTX 1050 Ti.使用Adam 优化方法，图5 所示为所选取的卷积神经网络在不同学习率(learning rate，LR)设置情况下的均方根误差随迭代步数的变化，最终初始学习速率设定为0.001.整个卷积神经网络的训练过程时长约30 min.

图5 不同学习率设置情况下均方根误差随迭代步数变化Fig.5 Evolution of RSME under different learning rates

3.2 二维温度、浓度重建结果

为探究测量噪声对重建结果的影响，在输入矩阵即归一化2 f/1 f 信号投影矩阵的真实值中引入一定水平的随机高斯噪声.图6 和图7 分别为无噪声和5%的噪声水平下，两种典型的火焰场1 和2的二维温度、浓度重建结果，其中ΔT 为重建温度值与真实温度值之差，为重建浓度值与真实浓度值之差.火焰场1 由两个位置靠近的二维高斯分布场叠加，在无噪声时，二维温度、浓度重建误差分别为1.43%和3.81%，在火焰分布边界处，重建值与真实值偏差较大，在5%的噪声水平下，二维温度、浓度重建误差分别为3.36%和4.04%，可知，引入随机噪声，二维重建误差有所增加，但卷积神经网络对噪声适应性较强，仍能实现高精度的二维重建效果.同理，对于火焰场2，其由两个位置相对远离的二维高斯分布场叠加，在无噪声时，二维温度、浓度重建误差分别为2.47%和3.72%，在5%的噪声水平下，二维温度、浓度重建误差分别为2.59%和4.14%.

图6 火焰场1二维重建结果Fig.6 Tomographic reconstruction results for flame 1

图7 火焰场2二维重建结果Fig.7 Tomographic reconstruction results for flame 2

在求解非线性层析重建问题时，传统方法多采用启发式算法，包括模拟退火算法、遗传算法等.就计算效率而言，以模拟退火算法为例，在同样的计算平台条件下，其完成样本数据集中单个样本温度或浓度场二维重建时长为10～15 h，而卷积神经网络完成单次重建所需时间约为ms 量级.因此，与传统非线性层析求解算法相比，深度学习方法在层析重建过程中计算效率大大提高，未来有望用于实际燃烧环境原位在线二维重建测量中.

进一步地，以二维温度场重建为例，对于500 个测试样本，在无噪声时平均重建误差为2.85%.不同噪声水平下的温度平均重建误差eT如图8(a)所示，随着噪声水平增加，重建误差增加，在20%噪声水平下重建误差平均值为4.75%，本文设计的卷积神经网络在高噪声水平时仍有较好的重建效果.

就噪声适应性而言，与本论文同步进行的一项研究工作[21]表明，在无噪声时模拟退火算法与卷积神经网络方法重建误差基本相同，在计算资源和效率允许的情况下，模拟退火算法也同样可以实现高精度温度或浓度场二维层析重建.然而，随着噪声水平增加，模拟退火算法的重建误差逐渐增大，而卷积神经网络方法表现出更优异的噪声适应性，原因在于卷积神经网络中包含多层卷积滤波运算，可进一步降低噪声对网络训练和重建效果的影响.

图8(b)所示为不同训练样本数对应的温度平均重建误差eT，当训练样本仅为1 000 时，重建误差值为4.16%，该方法可进一步推广至实际样本量有限情况下的二维温度场重建研究.总结来说，在非线性层析重建研究中，卷积神经网络可以实现高精度温度或浓度场二维重建，在计算效率、噪声适应性等方面都较传统模拟退火算法有极大的提升，这将进一步推动实际燃烧环境中实时、原位二维层析重建测量研究.

图8 不同噪声水平及不同训练样本数目对应的温度平均重建误差Fig.8 Average reconstruction errors of temperature distribution under different noise levels and numbers of training datasets

4 结论

本文主要开展了基于深度学习的免标定波长调制吸收光谱非线性层析重建算法研究.采用频分复用技术，构建非线性层析吸收光谱重建方案，对5 支激光器以不同调制频率进行高频调制，选取2 个投影角度，共计20 条投影光线.仿真中采用的火焰场为两个不同位置、不同形状的二维高斯温度、浓度分布场的叠加，用以模拟实际燃烧中火焰的非对称性.总仿真样本数目为10 000，构建卷积神经网络，初步实现二维温度、浓度场重建算法研究，主要结论如下：

(1) 本文设计的深度学习算法，可实现良好的温度、浓度重建效果，以火焰场1 为例，在无噪声时，二维温度、浓度重建误差分别为1.43%和3.81%，在5%的噪声水平下，二维温度、浓度重建误差分别为3.36%和4.04%.

(2) 随着噪声水平增加，温度平均重建误差增加，在20%水平下重建误差平均值为4.75%；随着训练样本数减少，温度平均重建误差增加，当训练样本仅为1 000 时，重建误差值为4.16%.研究表明，该方法可进一步推广至实际高噪声水平、样本量有限情况下的二维温度场重建研究.

后续工作将围绕最优吸收谱线选择、投影光线布置和数目设计、卷积神经网络结构的优化等方面开展进一步的温度、浓度场二维重建研究，服务于包含高温、低组分浓度等苛刻条件的复杂燃烧流场空间分辨实验测量.