煤粉气流着火机理及最佳煤粉浓度的分析
魏小林
(1.中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190;2.中国科学院大学工程科学学院,北京100049)
煤炭一直是我国最重要的一次能源,是工业用能的压舱石,预计未来几十年也会占能源消耗的50%以上,因此煤炭高效清洁利用得到国家的高度重视.我国大部分煤炭通过煤粉燃烧所消耗,但燃烧用煤的煤质与国外有较大差别,经常燃用灰分高、挥发分较低的煤,着火稳定性差(特别是对于小容量锅炉),而发达国家多燃用烟煤、褐煤等高挥发分煤.虽然国外从20 世纪60 年代起就在煤粉燃烧基础研究方面做出了系统性的开创成果[1-2],但是我国从70 年代起在煤粉稳燃技术方面也做出了自己独特性的系列成果[3-4].在目前“双碳”背景下,火电机组深度调峰运行是消除电源侧与电网侧双随机扰动、提高可再生能源消纳率的有效措施,煤粉稳燃技术是火电机组深度调峰的重要支撑.
周怀春等[5]总结了国内主要大学和中科院等在煤粉稳燃技术方面的研发历程,分析了国内大量的专利技术,认为我国从80 年代开始的煤粉稳燃技术可以归为两类:一类是借鉴国外旋流燃烧器[6],以烟气回流为主要技术特征,体现在1985 年4 月1 日开始申请的徐旭常等国内很多学者的专利内容上[7],包括预热室和各种钝体燃烧器,其原理是通过强化高温烟气回流,实现煤粉气流的快速加热和着火;另一类借鉴国外的WR、PM 燃烧器和W 型火焰锅炉旋风分离式燃烧器等[8],以煤粉浓淡分离为主要技术特征,体现在1989 年1 月14 日开始申请的徐通模等国内很多学者专利内容上[9],包括应用于直流或旋流燃烧器上的多种煤粉分离方式,其原理是将一次风分离为浓淡两股煤粉气流,首先实现浓煤粉气流的着火;并在四角切圆煤粉锅炉上采用水平浓淡燃烧技术时,强调充分发挥向火侧高浓度煤粉气流的着火优势[10].国内学者多年的研究与实践表明[11-13],烟气回流强化了煤粉的预加热过程,而浓煤粉气流也有自身的着火优势,两者的有机结合才是煤粉稳定着火的关键.
徐旭常等[14]在总结煤粉预燃室及火焰稳定船的作用时,强调在煤粉燃烧过程中,合理组织气流,形成局部的高煤粉浓度、高温和合适氧浓度的区域,成为稳定的着火有利区,是保证煤粉稳定燃烧的关键.可见,上述两类煤粉稳燃技术的基本原理均与此理论观点相符.由于在浓煤粉气流中,空气质量流率相对下降,因此在有利于煤粉着火的局部高温区,煤粉与空气的质量比是很重要的参数,因其直接代表了高温区的煤氧比,从而寻找所谓的“最佳煤粉浓度”变得重要起来.虽然煤粉浓淡燃烧的研究与应用已经较多,但是在氧燃料燃烧、高温空气燃烧和燃煤电站灵活性改造时的煤粉稳燃等领域,仍然需要高浓度煤粉燃烧研究的基础支撑.
煤粉挥发分含量越高,着火所需的空气量也越多,因此高挥发分煤的最佳煤粉浓度较低.国外最早开展了煤粉气流的层流火焰传播速度研究[15],并实际测量得到了最佳煤粉浓度[16-17].国内阎维平和徐明厚等较早开展了高浓度煤粉的燃烧研究[18-19],许多学者得到了不同挥发分煤粉的最佳浓度[18-23].一般在实验测量中认为煤粉气流燃烧过程中对应于炉内最高火焰温度[18]或者最短着火距离[19]的煤粉浓度为最佳煤粉浓度.
由于在常温条件下煤粉很难着火,因此煤粉气流着火的关键是一次风射流通过高温热烟气的热对流和辐射加热(实际锅炉中后者的影响较小),使得煤粉气流温度升高到煤粉的着火温度,这时煤粉所需的着火热等于着火区域供给的热量.传统认为煤粉气流的着火温度和着火热不但与煤粉气流本身的特性(煤粉挥发分与水分、灰分含量、浓度与细度、粒径分布以及煤粉气流初始温度、一次风率、风速等)相关[16],同时其着火的供给热也受到炉内加热方式与条件的影响.此外,由于煤粉燃烧时间较长,因此一般认为煤粉气流的火焰锋面十分厚,其内的温度梯度相当小,火焰锋面向新鲜煤粉与一次风混合物的导热及辐射很弱.由于气体预混燃料着火时,火焰锋面很薄,其内温度梯度相当大,燃料气流的预热主要来自于火焰区的导热[24],因此传统认为煤粉气流着火机理与气体燃料预混着火燃烧机理完全不同.
另一方面,在气体燃料预混燃烧时存在一个在当量比附近的燃料浓度,这时对应最大的层流火焰传播速度.由于气体预混燃料通过火焰锋面的导热即可加热至着火状态[24],因此气体预混燃料在常温下即可点燃.如果燃料的初始温度提高,虽然层流火焰传播速度增加,但是对应最大速度的燃料浓度几乎不会发生变化,因此层流火焰传播速度作为燃料的着火与燃烧基本特性受到广泛重视.在模拟煤粉气流燃烧时,Smoot 等[15]建立的一维分区模型,较早通过分区考虑了煤粉气流燃烧时预热区、火焰区和后燃区的不同辐射传热方式.由于气体-颗粒混合物存在爆炸的风险,因此近年来仍有不少工作研究了粉料气流的层流火焰传播问题[25-26],基于分区模型建立了计算预混粉料气流火焰传播速度的方法.
本文在深入分析煤粉气流着火过程时,发现煤粉气流着火机理本质上与气体燃料有着类似之处.煤粉气流着火过程仍存在着明显的火焰面,着火前释放的挥发分相当于为着火准备足够的预混可燃物,这些可燃物着火燃烧后也会通过导热进一步预热煤粉(除炉内高温火焰外在加热外),使得煤粉气流快速升温,并达到着火条件.
本文在以上研究与理论分析基础上,借鉴气体层流预混燃烧的分区着火机理,从层流煤粉燃烧火焰分析入手,提出以挥发分和少量焦炭燃烧热量作为着火供给热来评估煤粉气流着火状况的新思路,同时将不同区域的热量衡算进行解耦,探究煤粉浓度对于煤粉气流着火影响的基本特性,从而得到煤粉着火的分区机理.将煤粉气流的着火规律主要看作由其自身特性(浓度、温度、细度、速度、挥发分含量等)所决定,较大地简化了前人对于煤粉气流复杂着火过程的描述.在此基础上,还预测得到了煤粉最佳浓度,并提出着火供给热参量概念,可以用来对比分析不同浓度煤粉气流的着火特性.
1 煤粉燃烧的过程
为了研究煤粉气流的着火机理,先从实际锅炉的煤粉燃烧模拟结果了解煤粉气流的基本着火过程.图1 和图2 为国内一台300 MW 四角布置煤粉锅炉的数值模拟结果(B 层一次风截面),燃烧器采用了水平浓淡燃烧器,煤种为神华烟煤.从这些炉内速度场、温度场和浓度场的结果看,煤粉气流进入炉内0.5 m 左右的距离后(对应实际锅炉煤粉气流刚进入炉内存在0.3~0.5 m 的“黑龙”),很快就在一次风射流外围实现稳定着火,当射流进入炉内3 m 左右后,煤粉射流基本实现了内外完全着火.从这些煤粉气流根部着火段的模拟结果来看,围绕煤粉射流,存在明显的温度和CO、CO2浓度快速上升,以及O2突然下降的局部区域,这就是煤粉气流着火的核心区,即煤粉着火火焰.

图1 四角布置煤粉锅炉的速度场和温度场Fig.1 Velocity field and temperature field of pulverized coal in tangential corner fired boiler

图2 四角布置煤粉锅炉的浓度场Fig.2 Concentration distribution of pulverized coal in tangential corner fired boiler
在实际锅炉煤粉气流的着火过程中,煤粉进入炉内后,受到气流外围的对流和辐射加热,开始升温并释放挥发分,达到煤粉气流着火温度后,即发生已释放挥发分和少量焦炭的着火燃烧反应.由于存在这种高速反应、快速升温的放热过程,因此形成了稳定的煤粉燃烧火焰面.Horton 等[27]在测量层流预混煤粉火焰时,发现煤粉气流存在厚度只有10 mm 左右的火焰面.虽然煤粉燃烧属于典型的湍流燃烧,但是当讨论局部区域的微小火焰时,煤粉颗粒燃烧可以形成明显的火焰[28],因此层流燃烧的火焰面模型仍可以在此适用[29].
由于分析实际锅炉的煤粉加热过程是比较复杂的,因此下文先从层流预混煤粉的预热和着火过程进行分析.
2 煤粉气流着火理论分析
2.1 理论基础
许多研究者对于粉料气流着火进行过稳态或非稳态的理论分析[15,25-26].一般可以将煤粉气流的着火过程分为预热区、火焰区和燃尽区[15],图3 描述了一种典型的煤粉气流着火过程.

图3 煤粉气流的着火过程Fig.3 Ignition process of pulverized coal flow
综合分析这些模型,结合已有实验研究和数值模拟的结果,本文提出以下主要观点:
(1) 一般煤粉气流预热区的长度较长(~m 量级),虽然煤粉燃尽的时间比气体燃料长很多,但是根据实验研究和数值模拟[15,28]以及以上大型锅炉的数值模拟结果,煤粉气流着火和主要燃烧过程却很短,可以认为存在很薄的1~10 mm 量级厚度的着火火焰区(气体燃料的火焰面厚度更薄,一般为0.1~1 mm),因此在分析煤粉着火过程时,照样可以借鉴气体预混燃料着火过程火焰的分析理论.虽然此假设对于煤粉燃尽过程的研究是不够的,但是对于煤粉气流的着火过程分析是基本可靠的.
(2) 煤粉气流的预热可以分为两个过程(见图4),在一次预热区内煤粉气流依靠炉内对流和辐射加热,达到通常讲的煤粉气流着火温度;对于实际煤粉锅炉,此时的加热方式主要来自于煤粉射流外围的对流加热[30],因此可以称此着火热量为“外在供给着火热”.离开一次预热区后,煤粉气流进入火焰区,为了与煤粉气流一次预热区加以区分,这里称火焰预热区为煤粉气流着火的二次预热区,即火焰区可以分为两个子过程:二次预热区和着火反应区[24].在二次预热区内不发生反应,只接受来自后面相邻反应区的热传导加热,此热量由于直接来自煤粉气流着火后的自身热量,可以称该着火热量为“内在供给着火热”(前人在煤粉气流着火机理分析中,很少有人关注此热量).内在供给着火热使得煤粉气流在二次预热区进一步加热,达到煤粉颗粒的着火温度,此温度与通常讲的煤粉单颗粒着火温度非常接近,这时在反应区内将发生已释放挥发分和少量焦炭的快速着火燃烧过程,从而与二次预热区共同形成煤粉气流着火过程的火焰锋面.

图4 煤粉气流着火过程的分区模型Fig.4 Zonal model of ignition of pulverized coal flow
(3) 在实际煤粉燃烧过程中,煤粉气流被加热的方式主要为对流和辐射,从理论上进行煤粉加热过程的定量化分析是比较困难的,因此可以主要关注煤粉气流本身被加热的程度,其主要参数为煤粉加热过程的时间和终温,因为这两者才是影响挥发分释放和煤粉着火的核心要素.煤粉加热的时间和终温(其实就相当于升温速率)决定了煤粉气流在加热过程中挥发分的释放量,同时也决定了是否达到了煤粉气流的着火温度.由于单颗粒煤粉着火时,煤粉释放的挥发分热量很少,无法形成像煤粉气流着火过程的火焰锋面,继而向前传导热量,进一步加热煤粉,因此单颗粒着火的热量基本来自于外在热.研究表明,单颗粒煤粉的着火温度通常比煤粉气流的着火温度大300 ℃左右[16],因此以上分析中一次预热温度和二次预热温度的差别正好解释了此问题.可见,已有文献中得到的大量单颗粒煤粉着火温度和非均相着火数据,可以在实际锅炉煤粉气流着火机理的研究中被采用,因为该温度相当于煤粉气流二次预热区的出口 温度.
(4) 以上理论简单认为煤粉气流经过二次预热后,达到单颗粒煤粉着火条件即实现了煤粉气流的着火,将煤粉气流的着火机理只作为煤粉气流的“本身特征”进行分析,从而实现了煤粉气流着火机理与气体预混燃料着火机理的基本统一.该理论放弃了前人认为的煤粉气流着火与各种燃烧设备运行工况和燃烧器等具体因素的复杂关联性,将煤粉气流着火机理简单化地类同于气体预混燃料着火机理.显然这种认识还只是初步的尝试,需要不断深入探究.
2.2 煤粉气流着火过程的理论模型
在以上理论分析基础上,建立煤粉气流预热与反应区的着火模型,并假设如下:
(1) 在进行理论分析时,先避免分析实际复杂的煤粉加热着火过程,认为煤粉气流着火燃烧前,首先在一次预热区通过传热进行升温,并逐渐释放出挥发分,为着火准备充足的易燃物质;然后进入着火反应区,火焰区与一般的气体火焰有所类似,可分为二次预热区和反应区,在二次预热区内通过导热达到最终的着火温度.当煤粉气流达到一定温度时在反应区内开始着火燃烧,煤粉气流火焰特性主要由升温速率以及当地的已释放挥发分和可燃焦炭量等决定.
(2) 借鉴 Spalding 的气体层流预混燃烧理 论[24],假设在一次预热区释放的挥发分与空气已经充分混合,在火焰的二次预热区几乎不存在燃烧反应,没有热量释放,主要靠反应区的热量通过热传导,进一步加热煤粉气流中的可燃(主要是已释放的挥发分)混合物,而在反应区发生快速的气体反应(也可能有少量焦炭氧化反应发生,即发生非均相着火),释放出大量的热量,使得煤粉气流快速升温,从而维持煤粉气流的持续燃烧和焦炭燃尽.
(3) 煤粉气流中的焦炭燃尽时间(空间量级~ 10 m;时间量级~1 s)较长,虽然反应区也比通常的气体火焰长得多,但是本文主要探讨煤粉气流的着火机理,对于焦炭燃尽过程不做分析,从而主要考虑着火区附近的燃烧反应.同时,为获得主要的煤粉气流着火特性,将过程分析进行简化,不考虑颗粒和气流的温差以及它们之间的传热问题.
(4) 煤粉气流的热平衡方程可以写为

式中:ΔQa,p为煤粉颗粒和空气流被加热的总热量,方程右侧4 项分别为煤粉气流由于对流、辐射、燃烧和外在(如电热等)加热获得的热量.由于与一次预热区的加热长度(实际煤粉气流着火前距喷口300~500 mm)相比,二次预热区的火焰厚度很薄(1~10 mm),因此假设一次预热区加热量主要来自对流和辐射,而二次预热区的加热量主要来自火焰本身反应区的导热.反应区的热量主要来自释放的挥发分和少量焦炭的燃烧放热,同时考虑其对于二次预热区的向前热传导热量,但暂不考虑火焰反应区的辐射换热.从而将不同区域的加热方式分别考虑,实现了热量衡算的解耦.
3 层流预混煤粉气流的着火分析
3.1 层流预混煤粉火焰
通常的气体火焰是一个以亚音速、自维持传播的局部燃烧区域[24].假定火焰是一维的而且未燃气体以垂直于火焰面的方向流向火焰,这个流动速度就是火焰传播速度LS .在分析煤粉气流的着火问题时,为了简化问题并探讨着火的本质特征,如前所述,本文将层流预混煤粉气流的着火问题类比为气体层流火焰.由于煤粉火焰着火段的快速反应区同样很薄,因此该区域的温度梯度和组分浓度梯度仍然很大,从而可以将自由基组分通过热扩散,将热量通过热传导,快速传递到预热区,为火焰的持续发生提供物质和能量源.
以下为煤粉气流火焰的分区能量平衡方程:
3.1.1 一次预热区
在进行理论分析时并不去求解火焰微元控制体的组分和能量微分方程,而只是将控制体作为一个整体来考虑其物质和能量平衡.在一次预热区内,将煤粉气流的进出口和扩张边界作为控制体的边界(见图4),假设扩张边界不与煤粉气流有物质和能量的交换,可以得到简单的质量和能量平衡方程(推导过程见附录1).

一次预热区内煤粉随着温度的升高,逐渐释放出挥发分,是煤粉着火的关键因素.将挥发分的释放方程进行积分,即可得到一次预热区内煤粉挥发分的释放量(具体见附录2).

3.1.2 着火反应区
在二次预热区内,进入控制体的物质流与上面一次预热区的相同.在能量平衡分析时,将煤粉分为已经释放的挥发分和残余的焦炭,离开一次预热区的能量即为进入二次预热区控制体的能量,该能量加上反应区通过热传导进入二次预热区的能量,即为离开二次预热区的能量.由于反应区的热传导计算需要已知反应区厚度等数据,准确计算有一定困难,因此本文假设二次预热区的煤粉气流终温为单颗粒煤粉的着火温度Ti,p(作为已知值),这样可以给出二次预热区的能量平衡方程:

式中:方程右侧中方括号各项分别代表空气、挥发分和焦炭的影响.一般在层流预混火焰反应区内,离开二次预热区的温度可以视为预混气初温和反应后气体温度的平均值[24],本文借鉴此假设来确定一次预热区出口温度(即上式中的Tu)和反应区出口温度(即bT)的关系,因此并不直接求解公式(4).
计算反应区出口温度时,将二次预热区与反应区作为一个控制体考虑,反应区释热量只考虑已经析出挥发分的燃烧放热量(此处针对下文方法验证中烟煤的计算,暂不考虑少量焦炭燃烧释放的能量),从而整个控制体的能量平衡方程为

式(5)与二次预热区能量方程的差别在于右侧第一项的温度为着火反应区出口温度Tb.挥发分燃烧释放热量采用式(6)计算:


式中:Var为煤粉工业分析的挥发分质量份额;FC,ar为煤粉工业分析的焦炭质量份额;Qnet,ar为煤粉的低位发热量;每kg 碳的热值为32 800 kJ.
3.2 层流预混煤粉火焰的计算
具体计算过程如下:
(1) 在计算时,假设煤粉火焰二次预热区的出口温度等于煤粉单颗粒的着火温度,因此可以采用文献中不同煤种大量单颗粒测量的着火温度作为“真正”的煤粉气流着火温度.在计算挥发分释放量时,将煤粒的终温作为已知值,认为是一次预热区出口温度(先采用预估值),预热区的加热时间先根据煤粉气流的速度进行预估.
(2) 将经过一次预热区后挥发分的释放量确定好后,即可计算挥发分燃烧的热量,先假设已经释放挥发分发生快速燃烧,形成类似于气体燃料的层流预混火焰,按照其放热量得到火焰反应区出口的温度预估值.然后借鉴Spalding 的气体层流预混火焰,假设二次预热区出口的温度(即单颗粒煤粉的着火温度Ti,p)等于火焰反应区出口和二次预热区进口温度的平均值,这样就可以计算得到二次预热区进口温度,也就是一次预热区出口温度.
(3) 采用新的预热区出口温度,重新计算挥发分释放量,不断迭代,直到计算的一次预热温度、煤粉气流加热时间等与预估值一致,即可得到符合着火条件的工况参数(包括煤粉浓度、不同区域温度等),从而可以预测出最佳煤粉浓度等.
3.3 层流预混煤粉火焰计算结果的验证
在具体应用以上理论分析方法时,本文选择了Csaba 测量层流煤粉火焰传播速度时的经典实验装置作为研究对象[1,19],建立能量与热量平衡方程,研究煤粉气流着火机理及最佳煤粉浓度.Csaba 采用的燃烧室上部是一个高0.84 m、半角3°、进口直径0.05 m 的隔热圆锥体,下部是一个相连的耐火砖砌成的燃烧室.实验时调节煤粉气流速度和浓度,使得火焰前沿保持在距圆锥体进口0.6 m 处,在此位置,布置有火焰观察孔,对应的直径为0.1 m.在此位置之上,布置有4 个测量壁面温度的热电偶,在此之下,布置有7 个火焰温度测点.火焰传播速度换算为直径0.1 m 处(即距圆锥体进口0.6 m 高度处位置)时煤粉气流所对应的速度.实验用煤的收到基挥发分33%、水分3%、灰分13%,理论空气量为6.9 m3/kg,低位热值为6 300×4.186 8 kJ/kg,按比表面积平均的粒径为56µm.
Csaba 的实验装置不存在热气流的回流区,因此煤粉着火前的主要加热源为火焰区的辐射热,实际燃烧过程的煤粉气流加热方式当然也可以来源于热对流和热气流的混合等,但本文暂不涉及其计算.将该辐射热假设为煤粉气流直接吸收的火焰辐射热加上穿过煤粉气流到达隔热圆锥体后发射进入煤粉气流的辐射热,与Csaba[1,19]采用的辐射计算方法有所不同.从火焰进入煤粉一次预热区的辐射热表达为

式中:εf为火焰黑度,取为0.9;εb为隔热圆锥体的壁面黑度,取为0.8;k 为煤粉的辐射吸收减弱系数,用式(9)计算[31]:

式中:GP为煤粉颗粒的质量浓度,kg/m3;dP为颗粒直径;ρP为颗粒密度.
煤粉气流着火前的区域(从燃烧室顶部到0.6 m处)围成了一个圆台(上下圆面直径为 0.05 m 和0.1 m),可以计算得到其整个包壁辐射的平均射线行程(L=3.6 V/S)仅为0.006 95 m.
计算时预热区和火焰区需要相互迭代计算,通过火焰区热平衡方程(5)预测得到进口温度(Tu),针对一次预热区,即可通过公式(2)算得煤粉气流的层流火焰传播速度(uu).
图5 给出了煤粉燃烧的层流火焰传播速度理论计算值与实验值的对比,两者的基本趋势基本一致,特别是对于高煤粉浓度的工况.在较低煤粉浓度时虽然火焰传播速度有较大的实验结果,但是数据也存在较大的波动性.可以看出,在煤粉质量浓度为0.32 kg(煤)/kg(空气)(这时对应燃烧室进口单位体积的煤粉质量浓度为0.4 kg/m3)时,计算得到的层流火焰传播速度最大(1.02 m/s).

图5 煤粉燃烧的层流火焰传播速度Fig.5 Laminar flame velocity of pulverized coal combustion
图6 给出了煤粉火焰的温度实验值(图中表示为黑色圆点)以及理论预测得到的着火反应区温度,其中Tu为一次预热区煤粉气流出口温度,Tb为反应区气流出口温度.随着煤粉浓度的提高,预热区的煤粉气流温度有所减小,但最大减小幅度不超过100 K;同样,挥发分燃烧后,反应区的出口温度有所上升,但最大上升幅度也不超过100 K.实验结果(参见图6)表明,火焰在煤粉质量浓度为0.48 kg(煤)/kg(空气)(对应燃烧室进口的煤粉质量浓度为0.6 kg/m3)时,火焰温度达到最大值(1 785 K).从图5 的计算结果看,这时火焰的传播速度(0.99 m/s)也接近于最大.可以看出,煤粉气流的层流火焰传播速度与火焰温度有很好的相关性,最大的火焰速度基本对应着最高的火焰温度.
4 实际煤粉气流的着火分析
4.1 已有分析
国内外已有不少研究结果关于煤粉气流着火的最佳煤粉浓度研究.一般认为,一次风中的氧是煤中挥发分着火和燃烧所需要的,根据此假设,作者推导出煤粉气流的最佳煤粉浓度与煤的挥发分含量和挥发分热值的乘积呈反比[22]:

式(10)反映了最佳煤粉浓度与挥发分燃烧释放的热量有着密切的关系.王学斌等[23]总结了西安交大的实验结果,表明最佳煤粉浓度随着煤质发热量与挥发分乘积的增大而降低,并拟合出一经验公式,与式(10)结果定性上是一致的.
表1 给出了根据公式(10)计算得到的最佳煤粉浓度,并与文献实验结果[18]进行了对照(一次风温分别为20 ℃和300 ℃).可以看出理论公式(10)仅考虑了煤粉气流中挥发分的着火需求,得到的最佳煤粉浓度随煤的挥发分减少而增加,其基本趋势是正确的.但是对于高挥发分烟煤,理论值比实验值小;对于低挥发分无烟煤,理论值又明显偏大.可见,采用煤粉气流中的氧气主要用于煤粉挥发分燃烧需求的假设,得到的最佳煤粉浓度与实际燃烧过程是不完全相符的.

表1 最佳煤粉浓度计算值与实验值(kg(煤)/kg(空气))Tab.1 Calculated and experimental data of optimal pulverized coal concentrations
这是由于现有的理论在解释最佳煤粉浓度的存在机理时,仅考虑了全部挥发分用于煤着火热的假设,没有考虑对于高挥发分煤,可能仅需要部分挥发分燃烧即可实现煤粉气流稳定着火.另一方面,在实际煤粉燃烧的高加热速率(104~105K/s)过程中,煤粉着火的机理往往是两者结合的联合着火模式[16],因此在分析低挥发分煤的着火问题时,除考虑挥发分的均相着火外,还需要考虑焦炭的非均相着火.
4.2 实际煤粉气流着火的最佳煤粉浓度
阎维平等[21]采用煤粉气流着火热量供需平衡的原理,对存在最佳煤粉浓度的机理进行了分析,认为煤粉气流着火所需热量与着火区供热量相等、火焰温度水平最高时对应的煤粉浓度为最佳浓度,同时认为空气所提供的氧气需要足够满足挥发分着火及焦炭初期燃烧的需要.
盛昌栋等[32]在管式炉上研究了煤粉气流着火方式与煤粉浓度的关系,结果表明,当煤粉浓度由高向低变化时,煤粉气流的着火方式由均相着火向多相着火过渡,少量焦炭也参与着火燃烧;煤的挥发分含量越高,发生着火机理过渡的煤粉浓度越大.可见煤粉浓度变化时会影响焦炭的燃烧份额,从而影响煤粉气流的着火机制.
这里将前文的理论推广至实际煤粉气流的着火火焰,仍然假设煤粉气流着火存在一次预热区和火焰区,其中二次预热区出口的温度(即单颗粒煤粉的着火温度Ti,p)等于火焰反应区出口和二次预热区进口温度的平均值.当煤种确定后,着火温度Ti,p即为确定值,从而可以认为煤粉着火难易主要由挥发分和少量焦炭的燃烧放热量决定.
根据以上理论计算和文献中的研究,对于烟煤煤粉,本文假设煤粉气流着火时大约40%的挥发分和约1%的焦炭已经发生反应,可以作为着火的判断条件;对于低挥发分煤,由于着火温度更高,假设大部分释放的挥发分和大约5%的焦炭发生氧化.以下计算根据不同煤种设定了不同的挥发分和焦炭燃烧份额.
若煤粉气流中每千克空气的煤粉质量浓度为µ,假设煤粉气流中空气刚好满足煤粉已释放挥发分和少量焦炭的燃烧所需,则有

式中:挥发分燃烧所需的理论空气量V0,v采用可燃基的煤粉理论空气量进行估算;εch为着火燃烧的少量焦炭质量份额;V0,ch为煤粉中固定碳燃烧所需的理论空气量,按纯碳计算:

这样最佳煤粉浓度即为
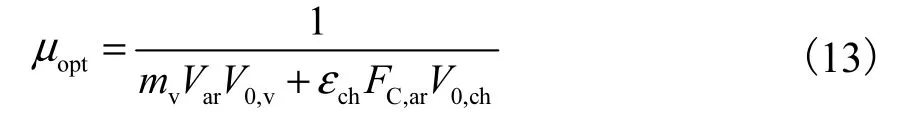
对于高挥发分煤,可以忽略焦炭燃烧对于着火的影响,显然最佳煤粉浓度与挥发分燃烧所需的理论空气量呈反比.由于燃料的发热量大体与理论空气量成正比(处于3.63~3.95 MJ/m3范围)[30],这时式(13)仍反映了最佳煤粉浓度与挥发分燃烧释放热量呈反比,只是对应的不是全部挥发分.而对于低挥发分煤,少量焦炭着火提供的热量就与挥发分相当了,这时着火热量将来自于几乎全部的挥发分和5%左右的焦炭燃烧热.
图7 给出采用式(13)预测的最佳煤粉浓度值,并与国内外文献中的实验值进行了比较.可以看出大多数的数据误差在15%以内,少数在30%以内,该方法比较广泛地适用于不同的煤种,基本是可靠的.

图7 最佳煤粉浓度预测值与实验值的比较Fig.7 Comparison of calculated and experimental data of optimal pulverized coal concentrations
4.3 煤粉浓度变化的影响和着火热
(1) 最小煤粉浓度
由于一次风中的空气量一般不会大于煤粉燃烧当量比下的空气量(因为还需要有二次风、三次风等),因此当煤粉气流中每千克空气的煤粉质量浓度为µ时,可以假设煤粉气流中空气刚好满足全部煤粉的燃烧所需(因为这时刚好符合煤粉-空气的当量比条件),则有

其中燃烧所需的理论空气量为V0,ar,从而可以定义煤粉气流着火的最小煤粉浓度为

(2) 着火供给热
一般煤粉气流着火热量被定义为将1 kg 空气和µkg 煤粉加热到着火温度所需吸收的热量[21],采用该方法得到的着火热将随煤粉浓度µ线性增加,因此需要精确计算供给热量然后才能获得最佳煤粉浓度,这对于实际锅炉燃烧过程是比较困难的.
考虑到煤粉气流的内在着火供给热主要来源于火焰反应区,本文提出将煤粉气流的着火热重新定义为特定煤种单位质量煤粉气流可以供给的内在着火燃烧热,即

式(16)右侧括号中两项分别为煤粉气流着火时挥发分和少量焦炭燃烧所提供的着火热(其中右侧分母中除以2 代表只有一半燃烧热供给了煤粉气流的预热热量).可以看出,当煤粉浓度µ 增加时,µ/(1+µ)虽然也有所增加,但是不会线性增加.式(16)分母中若考虑了煤粉气流的比热,显然该式表示的含义即为着火燃烧热释放后所能够提供的煤粉气流升温程度(即火焰区进出口温差),显然该值越大,则煤粉气流越容易着火,因为这时煤粉气流的燃烧温度将处于更高水平,从而对应最佳煤粉浓度.所以,当煤种确定后,上述内在着火供给热是判断煤粉气流着火状况的核心因素.
(3) 着火供给热参量
在分析最佳煤粉浓度的存在原因时,为了比较不同煤粉浓度下的着火供给热大小,理想化地认为煤粉气流的挥发分析出量(vm)和焦炭着火燃烧质量份额(εch)均为定值(假设其都对应最佳煤粉浓度时的值),从而煤粉浓度变化对于着火的影响特性就可以简单地由式(17)决定


这时着火供给热参量达到最大.在最佳煤粉浓度下着火时,由于空气已经被挥发分和少量焦炭的着火燃烧完全耗尽,再继续增加煤粉浓度,将不会提供更多的燃烧热,因此当煤粉浓度大于μopt时,式(17)就成为

由于这时分子μopt不变,显然随着煤粉浓度的增加,将不断下降,从而使得在最佳煤粉浓度下处于最大值.
(4) 最大煤粉浓度
为了讨论煤粉浓度变化对于着火机制的影响,采用以下方法估计煤粉气流的最大煤粉浓度,从而确定煤粉浓度潜在的最大变化范围.
最小煤粉浓度由式(15)确定后,可以假设存在一个最大煤粉浓度,这时煤粉气流的着火供给热参量与最小煤粉浓度下的值相等,这是因为煤粉浓度大于最佳浓度后再继续增加煤粉浓度,着火供给热将不断减少,在最大煤粉浓度时,与最小煤粉浓度时相比,两者均对应相同的最低着火热,因此最大煤粉浓度将满足:

因此最大煤粉浓度可以采用式(21)确定:

(5) 算例
针对Csaba 实验所用烟煤,根据式(15)和式(21)可以计算得到最小、最大煤粉浓度为0.112 kg(煤)/ kg(空气)和4.20 kg(煤)/kg(空气).图8 给出了着火供给热参量随煤粉浓度的变化规律,可以看出该曲线描述了最佳煤粉浓度的存在原因.在实际煤粉火焰中,锅炉还要送二次风和三次风,即实际一次风气流的最小煤粉浓度要比理论值大得多;另外,考虑到煤粉气流的输送,一般最大的煤粉浓度最多为3~5 kg(煤)/kg(空气),因此图中的最小、最大煤粉浓度数据只是理论上的,实际的煤粉浓度变化范围比图中要窄些.
值得注意的是,虽然图8 在理论上解释了煤粉气流存在最佳煤粉浓度的原因,但是在针对Csaba 实验所用烟煤的着火燃烧研究中,发现当煤粉浓度为μopt时,挥发分释放率约40%;但当煤粉浓度为μmin时,挥发分实际释放率将增加至90%以上;而当煤粉浓度为μmax时,挥发分释放率将小于10%.可见,在实际的煤粉气流着火中,当煤粉浓度降低时,为了实现稳定着火,煤粉气流将“自适应”地使得煤粉预热的时间适当延长,并使对应的一次预热区出口温度上升,从而煤粉释放挥发分的份额将增加;直到对应最小煤粉浓度(μmin)时,煤粉气流中几乎所有的挥发分均释放出来用于煤粉着火,这时煤粉气流的着火将被推迟.当煤粉浓度增加时,将出现相反的情况,挥发分释放份额将不断减小.有趣的是,对于确定的煤种,虽然这时煤粉浓度发生大幅变化,但是μ/ (1 +μ)值几乎保持为一个常量,这也间接说明对于确定的煤种,其着火供给热参量()是不变的,从而对于浓淡煤粉燃烧器设计带来方便.当然,着火供给热参量对于不同煤种,特别是低挥发分煤,由于这时少量焦炭着火燃烧增加的着火热变得重要,其适用性还需要深入分析.

图8 煤粉气流着火供给热参量随煤粉浓度的变化特性Fig.8 Various heat supply parameters of pulverized coal flow ignition with pulverized coal concentrations
5 结论
本文借鉴气体层流预混燃烧的分区着火机理,从层流煤粉燃烧火焰分析入手,将煤粉气流着火过程分为一次、二次预热区和着火反应区,对于不同区域的热量衡算进行了解耦计算.煤粉气流在一次预热区主要受到来自炉内的对流和辐射(外在着火供给热),二次预热区主要接受后面着火反应区的导热(内在着火供给热),反应区的热量主要来自于已经释放挥发分和少量焦炭的燃烧热.本文认为二次预热区的出口温度为煤粉气流的真实着火温度,其接近于煤粉单颗粒的着火温度(该温度根据文献数据很容易确定);并提出将煤粉气流单位质量获得的着火反应热作为核心参数分析不同煤粉浓度时的着火特性,从而阐明了煤粉气流分区着火机理,获得了不同浓度影响煤粉气流着火的基本特性,并比较准确地预测出最佳煤粉浓度.最后,提出描述煤粉浓度变化时的着火供给热参量概念,将煤粉浓度影响着火特性的规律表达为

这对于实际高浓度煤粉燃烧器的设计,带来较大的方便.
致 谢
作者感谢德国RECOM 公司韩晓海博士提供了300 MW 锅炉燃烧的数值模拟结果.感谢研究生张乐宇、黄俊钦和孙岑等在模拟结果分析和制图、排版和修订等方面的协助,以及与徐通模教授和李森研究员的有益讨论.
符号表:
Ab—反应区气流出口面积,m2;
A0—一次预热区煤粉气流进口面积,m2;
Ai—二次预热区煤粉气流出口面积,m2;
Au—一次预热区煤粉气流出口面积,m2;
Av—挥发分释放时阿累尼乌斯反应速率常数中的频率因子,s-1;
cp,a—煤粉气流中空气定压比热,kJ/(kg·K);
cp,c—煤粉气流中煤粉定压比热,kJ/(kg·K);
cp,g—挥发分燃烧后热烟气定压比热,kJ/(kg·K);
dp—颗粒直径,m;
Ev—挥发分释放的活化能,kJ/kmol;
FC,ar—煤粉工业分析的收到基焦炭质量份额;
Gp—煤粉颗粒单位体积的质量浓度,kg/m3;
k—煤粉的辐射吸收减弱系数;
L—煤粉气流吸收辐射的平均射线行程,m;
mv—煤粉挥发分释放的质量份额;
qign—单位质量煤粉气流可以供给的着火燃烧热,kJ/kg;
Q—实际快速加热条件下煤粉挥发分释放量与工业分析挥发分量间的质量关系常数;
Qcom—煤粉气流中挥发分和少量焦炭的燃烧放热量,kJ/kg;
Qcon—进入煤粉气流的对流加热量,kJ/kg;
Qex—进入煤粉气流的其它外在加热量,kJ/kg;
Qnet,ar—煤粉的收到基低位发热量,kJ/kg;
Qrad—进入煤粉气流的辐射加热量,kJ/kg;
Qv—挥发分发热量,kJ/kg;
R—通用气体常数,8.314 kJ/(kmol·K);
t—从过程开始的时间,s;
T—绝对温度,K;
Tb—反应区气流出口温度,K;
T0—一次预热区煤粉气流进口温度,K;
Ti,p—单颗粒煤粉的着火温度,K;
Tu—一次预热区煤粉气流出口温度,K;
ub—反应区气流出口速度,m/s;
u0—一次预热区煤粉气流进口速度,m/s;
ui—二次预热区煤粉气流出口速度,m/s;
uu—一次预热区煤粉气流出口速度,m/s;
V—在时间t 内煤粉颗粒失重释放出的挥发分的质量百分数(占煤粉的质量分数,下同),%;
V∞—挥发分在实际反应器内可以释放挥发分的最大质量百分数,%;
Var—煤粉工业分析的收到基挥发分质量百分数,%;
Vc—在实际反应器内,由工业分析得出的焦炭仍能释放(残留在焦炭中)的挥发分质量份额;
Vp—工业分析的煤释放挥发分的质量百分数,%;
V0,ar—煤粉燃烧所需的理论空气量,kg/kg;
V0,ch—煤粉中固定碳燃烧所需的理论空气量,kg/kg;
V0,v—挥发分燃烧所需的理论空气量,kg/kg;
εb—隔热圆锥体的壁面黑度,文中取0.8;
εf—火焰黑度,文中取0.9;
εch—参与煤粉气流着火燃烧的少量焦炭质量份额;
µ—煤粉气流中每千克空气中煤粉的质量浓度,kg(煤)/kg(空气);
μopt—最佳煤粉浓度,kg(煤)/kg(空气);
ρb—反应区出口热气流的密度,kg/m3;
ρ0—一次预热区煤粉气流中空气的进口密度,kg/m3;
ρp—颗粒密度,kg/m3;
ρu—二次预热区煤粉气流中气体的出口密度,kg/m3;
σ—黑体辐射常数(斯蒂芬-玻尔兹曼常数),5.67×10 W/(m2·K4).
附录A 煤粉气流一次预热区的质量平衡与 能量平衡计算
文中图4 给出煤粉气流着火过程的分区模型.对于质量平衡,进入控制体的质量流率为

式中:u0为煤粉质量浓度,表示煤粉气流中单位质量空气所携带的煤粉质量;A0为煤粉气流进口面积.
离开一次预热区控制体的质量流率为

式中:Au为煤粉气流出口面积.虽然这时挥发分释放会造成气体质量份额增加和颗粒物质量份额减少,但是为了能量方程的计算简便,仍然认为离开控制体时煤粉气流中的煤粉质量浓度为μ0.
对于能量平衡,考虑到进出口温度和气流比热的变化,进入控制体的能量流:

式中:ca,p和cp,c分别为空气和煤粉的比热,计算时空气比热随温度升高,而煤粉比热可作为已释放挥发分和焦炭的混合物比热,也随温度有所增加.
离开一次预热区控制体的能量流:

这样可以给出以下能量平衡方程

正文中能量平衡方程(2)左侧只给出辐射加热项表达式,没有考虑对流加热项.
附录B 煤粉气流预热区内挥发分的释放计算
将预热区内煤粉的热解考虑为一步简单反应[2],挥发分的释放方程为

式中:V 为在热解时间t 内煤粉颗粒因失重释放出的挥发分的质量百分数(占煤粉的质量百分数);T 为煤粉颗粒的终温;V∞为煤中挥发分在反应器内快速升温时可以释放出的最大挥发分质量百分数,用式(B2)表示[1-2]

式中:Vp为工业分析的煤释放挥发分的质量百分数,考虑到在实际反应器内由工业分析得出的挥发分无法全部释放,有一小部分仍将残留在焦炭中;Vc为这部分焦炭仍能释放的挥发分的质量分数(占挥发分的质量),对于非膨胀性煤Vc可取为0.15[1-2];考虑到在实际反应器的快速加热条件下,Q 为煤粉挥发分释放量与工业分析挥发分量的质量比关系,对于一般的烟煤,Q 取值为1.26~1.44[1],而对于无烟煤或贫煤,此值要小一些.
将挥发分的释放方程进行积分,即可得到一次预热区内煤粉挥发分的释放量:

其中挥发分释放速率为


