关于第54届国际化学奥林匹克试题4-9的表观解离常数计算的讨论
张思翰,梁驰予,邱晓航
南开大学化学学院,天津 300071
锂离子电池的研究与应用已经对人们的生活产生了深远的影响。2019年诺贝尔化学奖便授予了John B. Goodenough,M.stanley Whittlingham以及Akira Yoshino三人,以表彰他们在锂离子电池发展方面做出的巨大贡献。传统的锂离子电池受到能量密度以及原料资源储量等方面的限制,难以满足现阶段大规模储能需求。新型的锂硫电池由于具有远高于商业锂电池的比容量(~1675 mAh·g-1,商用钴酸锂电池~150 mAh·g-1),以及低污染、环境友好等优势,具有极大的应用潜力[1,2]。
“穿梭效应”是限制锂硫电池发展的一个关键问题[3]。电池正极放电过程常伴随多硫化物的生成以及溶剂化,溶剂合多硫化物迁移至电池负极区与负极片直接反应,将导致电池容量不可逆地衰减。因此,研究多硫化物在常见的锂离子电解液中的溶剂化行为对锂硫电池的设计具有重要意义,2022年IChO笔试第4题便以此为背景设题,其中第4-9小题涉及了多构象化合物的平衡计算问题。阅卷、仲裁过程中发现,有许多同学由于对化学热力学概念理解不充分而失分。
1 题目与答案
4-9中[4],由于聚硫化物在DME中第二步解离常数极小(Kd1/Kd2≈ 1014),因此溶液中多硫化物主要以Li2S6(DME)以及其一级解离形式存在,可以将原平衡简化为如图1所示模型:

图1 简化的聚硫化物溶剂合平衡模型

最常见的错误解答(2)采用了与上式类似的方法计算,这种方法简单地将化合物Li2S6(DME)的吉布斯自由能视为两个构象吉布斯自由能的加权平均,再利用图中关系算出总解离反应自由能变,既而计算表观解离反应自由能变如下:

试题所参考论文中给出的表观解离常数如下[5]:
根据热力学基本原理[6],正确的解题方法是,将体系视为多重平衡,利用平衡时各物种之间浓度关系,列出表观平衡常数的表达式:

显然,方程(3)与(2)不等价。
2 热力学角度讨论
2.1 化学势推求
试题参考文献[5]的作者列出方程(1)的思路是,将总反应看作两个构象解离方程式按平衡时分配比例δI,δII的加和:

设构象I与构象II的总浓度为c,作者认为此时左侧的化学势表达式如下:

利用平衡时方程式左侧化学势等于右侧化学势的条件,能够得到方程(1)。
但如果进行严格推导,列出上述反应的自由能变,式中各项化学势可以根据van’t Hoff方程给出:

方程(10)结果与方程(3)等价,我们按照文献作者的思路进行的严格的热力学推导,却得出了不同的结论。(4)式的表示方法默认了两个构象按照一定的比例协同作用才可以解离。但是实际上,构象I与构象II的解离反应是独立的,并不是协同过程,因此,平衡时Li2S6(I)、Li2S6(II)与解离产物的化学势两两相等,如方程(11)。

这两种计算方式反映了对总反应方程式中系数的不同理解:式(4)表示构象I与构象II按照摩尔比δI: δII协同解离,而正确的理解应是,反应有δI的概率按照构象I的方式解离,δII的概率按照构象II的方式解离。
2.2 热力学过程图
为了进一步明确错误成因,可以绘出两个计算方法对应的热力学过程图,并给出其中每一过程的自由能变(图2)。
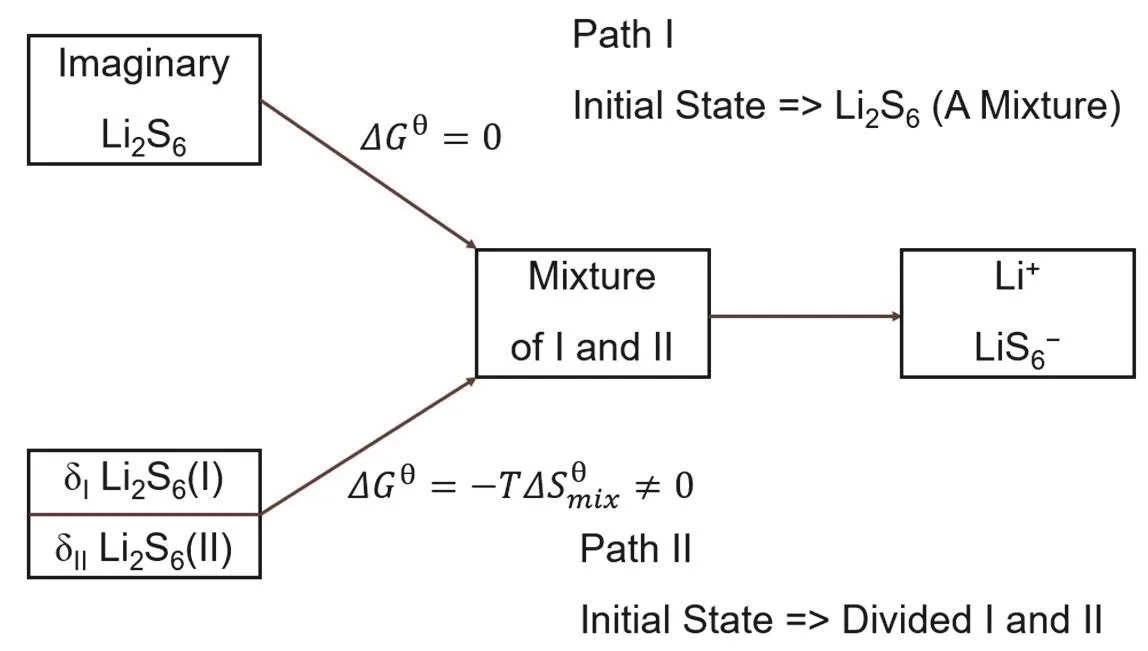
图2 仲裁过程中针对Q4-9所使用的解释性热力学状态图
对比可以发现,两种计算方法间正好相差了混合自由能变项。方程(2)相当于按照图2中路径II求算反应的自由能变,而方程(3)相当于按照反应路径I求算,两种方法的本质差异在于,计算反应物自由能时,是否考虑了构象混合所产生的熵变。
体系自由能变化与不同状态组成示意如图3所示。

图3 体系自由能变化与不同状态组成示意图
由于存在混合作用,图3中自由能的最低点应是考虑了混合作用的自由能曲线与平衡组成比线的交点,对应状态IV;若将两构象自由能的加权平均值作为反应物自由能,其所处状态为图3中不考虑混合线与平衡线的交点,对应状态III。
状态III的自由能的大小处于两个构象之间,具有向自由能较低构象转变的趋势,而这与两构象具有转化平衡、能够共存这一事实相违背。简单来说,状态III其实是一个理想的非稳态,体系中存在一个假想的隔板,将构象I与构象II分隔开,并阻止了构象间的相互转化。
从状态III到状态IV过程自由能变化可以选择两种途径进行计算。假设状态III中隔板两侧构象不发生转化,抽开隔板,两构象混合,此过程自由能变化可以使用混合自由能变公式求算:

同样,也可以保留隔板,使隔板两边均达到构象转化平衡,算出由状态III到状态V间的构象转化自由能变。状态V至状态IV间存在“吉布斯佯谬现象”,因为隔板两侧均达到构象转化平衡后,隔板两侧构象不可区分,由于体系的量子效应,因此过程V→IV过程计算熵变需要添加校正项,校正后此过程自由能变为0。
在针对此题的讨论过程中,错误理论的其中一种辩解思路便是将构象I与构象II认定为同一化合物,因此认为计算过程中存在“吉布斯佯谬”。判断一个混合过程是否存在“吉布斯佯谬”首先需要明确这一佯谬出现的条件:混合前隔板两侧粒子具有完全一致的内禀性质,状态III中,隔板两侧分别是纯的构象I与纯的构象II,两构象之间有明确的单点能差异与空间结构差异,内禀性质不同。假使隔板两侧交换一个分子,显然隔板两侧具有能量变化,其大小为一个分子在构象I与II之间转换的能量差,这一过程存在着能量变化。通过以上两点,可以发现状态III的混个过程与出现“吉布斯佯谬”所需隔板两侧粒子完全一致这一前提相矛盾,因此这一辩论思路是错误的。
3 统计物理学角度讨论
从上面的讨论可以看出,两种方法的差别来自于对多构象化合物热力学计算的不同认识。由于讨论的是平衡体系,不同系综具有等效性,下面使用恒定(T,p,N)条件使用等温等压系综,给出该体系的热力学函数表达形式[7,8],其中化学势可由(13)式求得:

对于本题所涉体系,构象I与构象II之间可以通过振转相互转化,可以视为处于两个不同能级上的粒子数满足玻尔兹曼分布定律:

由此可算出总解离反应自由能变,可证方程(18)与(3)等价。方程(18)中包含了由于混合作用导致的自由能变。据此,还可以合理外推出多构象的化合物摩尔化学势的计算方法:

4 总结讨论
根据以上讨论,我们可以发现导致方程(1)以及(2)错误的原因,是没有对物理化学基础理论与思想充分理解,并且主观臆断造成的。此外,清华大学张强教授于今年发表的一篇论文中,利用测定溶液电导率的方法对此体系的一级解离常数进行了实验验证[9],计算结果与实验结果对照如表1所示,实验值与方程(3)计算结果吻合较好。

表1 不同方法取得结果对照
从试题角度出发,此题仅涉及简单的物理化学知识,计算过程简单且直接。然而在实际的考试以及科研应用中,往往会由于基础物理化学概念不清导致出现与此题类似的错误。物理化学的学习不应仅满足于会列方程解方程,还要学会列什么方程以及为什么列这个方程,前者只要有足够的做题量积累很容易达到,但一旦涉及实际应用便容易手忙脚乱;后者需要的则是深入的思考与探究,对于各种理论,不仅知其然,更知其所以然,才能真正窥探物理化学的美感与其背后深刻的化学思维。

