基于复杂地块凸划分优化的多无人机覆盖路径规划
薛镇涛,陈建,*,张自超, 2,刘旭赞,苗宪盛,胡贵
1. 中国农业大学 工学院,北京 100083
2. 武汉大学 测绘遥感信息工程国家重点实验室,武汉 430079
在无人系统导航过程中,路径规划已经成为最值得研究的问题之一[1]。而其中的全覆盖路径规划[2](Coverage Path Planning)是无人系统规划1条避开所有障碍物且遍历目标地块的最短路径过程,在农业生产[3]、城市管理[4]、室内清扫[5]等方面都有较多的运用。在二维空间下全覆盖路径规划的运用背景和无人系统类型虽然大有不同,但最终规划目标基本相同,即在路径覆盖过程中,在保证覆盖所有目标区域以及尽量没有重复覆盖的前提下,使得总覆盖路径长度最短。
伴随无人机的广泛运用以及多无人机协同技术的发展,无人机飞行抗扰以及避障技术逐渐成熟[6],多无人机覆盖路径规划问题也逐渐成为了研究中的重点,如何让无人机在覆盖路径过程中能够节省能源、提高工作效率成为多无人机覆盖路径规划的重点和难点。而改善工作效率和能耗的关键就是在覆盖过程中尽量使得覆盖路径有效,通过优化缩短转移路径和减少转弯次数,可以保证无人系统的工作路径最优。
在以往的研究中,牛耕法作为最早的全覆盖路径规划方法成为了经典的无人系统行进规划方式。但在标准地块中,作业方向显然成为了影响牛耕法性能的重要因素,且一旦地块形状复杂则会使得作业轨迹无法闭合,无法完成全覆盖路径规划。根据地块的复杂程度,学者们不断在此基础上进行改进,针对不同环境给出了不同优化求解方法,在全覆盖路径规划综述[7-9]中也有所介绍。覆盖路径的方法大致分为经典算法和启发式算法,其中经典算法又分为图搜索法、单元分解法、线扫分解法、栅格法、人工势场法等,而启发式算法主要有遗传算法、模拟退火算法、粒子群(Partical Swarm Optimation, PSO)算法、蚁群算法、神经网络算法等。
在初始的地块轮廓方面,针对自然地块轮廓的不规则性和复杂性,有较多学者进行了研究。于靖等[10]就自然矢量岸线压缩问题提出了1种基于最小二乘法、通过筛选凸点三角形面积大小的改进的道格拉斯-普克(Douglas-Peucker)算法,在保证信息丢失度低的前提下有较好的压缩比。李星烨[11]在对轮廓凹点进行划分的过程中,通过讨论凹点形状,确定决策距离,从而进行近似消除,但对于形状特殊的凹多边形的处理仍然有缺陷。吴青坡等[12]对外界轮廓采用多边形宽度和最小外接矩形,对不规则多边形离散化求解,给出可以进行全覆盖路径规划的栅格图。
在凸划分覆盖地块方面,陈海等[13]通过对不含有障碍物的地块进行凸划分,建立划分后的衔接关系,并根据不同无人机的性能调整划分面积,给出合理的多无人机覆盖路径。戴健等[14]在对非凸区域的划分方法的讨论中,采用对凹点做分割线并旋转的方法,根据覆盖路径长度来确定凹口的分割角度,达到合理的凸划分,但对于其他划分情况依然没有考虑完全。Vinh等[15]对凹区域和复杂区域进行凸多边形包围,再进行多无人机覆盖路径任务的分配和协调,但凸多边形包围会导致地块的轮廓失真严重。Nielsen等[16]从多边形边上扩展,通过组合子地块保证整体最小宽度,从而保证覆盖路径较短,但没有考虑到算法对复杂地块的适用性。
在确保覆盖路径满足作业需求方面,Rantanen和Juhola[17]采用基于领域的方法过滤掉一些不必要的节点,改进后的随机路标法仍然保持较好的覆盖率,能够保证覆盖路径的完整性。Le等[18]将覆盖机器人设计为四菱形,并将整体地图设计成含有各种铺贴图案的多路点连接图,运用遗传算法以及蚁群算法优化最短路径,但对地块考虑过于简单。阚平等[19]为提高多植保无人机协同作业效率,在保证各架无人机满足约束的情况下,用改进PSO算法实现了无人机返航顺序和返航点位置的寻优。周林娜等[20]融合单元分解法与神经网络算法对矿区废弃地的全覆盖路径进行了优化。李楷等[21]基于回溯法,解决了局部区域覆盖过程中存在遗漏区域的问题,降低了覆盖路径的重叠率,给出1条光滑无障碍路径,但运用的是简单的栅格地图。Hassan和Liu[22]基于捕猎者-猎物方法通过开发新型的自适应覆盖路径规划方法,可以有效地实时响应边界变化并给出最小的成本实现完全覆盖,但是其方法基于简单的栅格地图。
而无人机路径规划也与覆盖路径规划问题有着较大相关性,Guo等[23]运用改进的深度增强学习的方法解决了无人机路径规划问题,并运用仿真证明了方法的有效性和优越性。Liu等[24]针对粒子群优化收敛慢与容易陷入局部最优的问题设计了1种空间精细投票机制,并引入时空碰撞避免技术来避免无人机的碰撞,规划出多无人机四维协调路径。Qu等[25]通过灰狼优化器与共生生物搜索混合算法,生成平滑的无人机飞行路径,加快了生成路径的收敛速度并保证整体搜索的能力。Liu等[26]提出1种基于双层规划的无人机实时路径规划方法,嵌入5种启发式优化策略的离散化算法用于加速规划,并在仿真中证明了该方法的效率和适用性。杜楠楠等[27]提出基于无向图搜索的方式,并通过混合整数线性规划的方法求解每架无人机的最优飞行路径。
以上文献都对地块优化和覆盖路径规划有突出贡献,但面对更加复杂的覆盖地块环境时,会逐渐暴露出以下问题:
1) 没能避免或减少凹多边形对于覆盖路径的直接影响,消除关键的凹点影响路径优化的最终效果。
2) 没有考虑有障碍物的凹多边形如何进行覆盖路径规划或者有障碍物的凹多边形如何进行凸划分优化。
针对以上问题,对含障碍物的复杂地块进行凸划分优化与覆盖路径规划研究。
1 复杂地块的定义以及轮廓近似压缩
在一般自然地形下,边界具有随机性,往往并不是规则图形,含有曲边和凹陷,边界崎岖,较难针对特征进行一定的分割。将不规则地块边界定义为含有曲线边缘且无顶点的地块边界,无法采用分割线DL对其进行有效分割,不规则边界显然成为地块分割的重要障碍,需要进行处理后才能进行划分操作,如图1所示。

图1 不规则边界无划分特征
复杂地块的定义为含有1个或1个以上的凹陷边缘且含有不规则地块边界的轮廓地块,而含有的复杂障碍物定义为含有不规则边界并完全包含于地块中的图块。因此,本文针对复杂地块及复杂障碍物无法进行凸划分处理,采用近似压缩的方法。较多前人研究过程中都会涉及到对于边界的确定,复杂的地块边界会影响覆盖路径算法效果,故需要对复杂地块进行简化。复杂地块轮廓对覆盖路径的影响如图2所示。

图2 复杂地块对覆盖路径的影响
多边形作为1种规则图形,将复杂地块的边界轮廓近似压缩为复杂多边形,只要保证边界压缩不高于一定的误差率,就可以使得地块边界压缩成为一定的复杂多边形。显然外轮廓和障碍物轮廓的压缩近似是不同的,假设地块轮廓外是可飞区域,但无需覆盖,而障碍物内部是禁飞区域,若覆盖路径越过,则会影响飞行安全,故需要分别进行讨论。
1.1 复杂地块的边界轮廓近似压缩
当目标覆盖地块的边界出现如边界为光滑曲线或者边界过于弯曲等复杂情况,使得目标地块为复杂地块,此时需要运用改进的Douglas-Peucker算法[10]对目标地块进行简化,首先需要对连续边界进行矢量化规定,按照逆时针对边界进行排序,之后运用Douglas-Peucker算法对曲线二分近似,得到后期可以进行凸划分的外部轮廓, Douglas-Peucker算法的步骤如图3所示。整体算法流程如下:
步骤1原本的复杂边界,进行链码操作,得到边界各个像素点的顺序。
步骤2边界线被分割为基于端点的线段,并寻找最远点。
步骤3找到相距初始线段垂直距离最远顶点并不断连接,并重复步骤2。
步骤4当循环后的线段垂直距离平均误差低于给定误差,认为多边形近似建立成功,连接各个顶点。
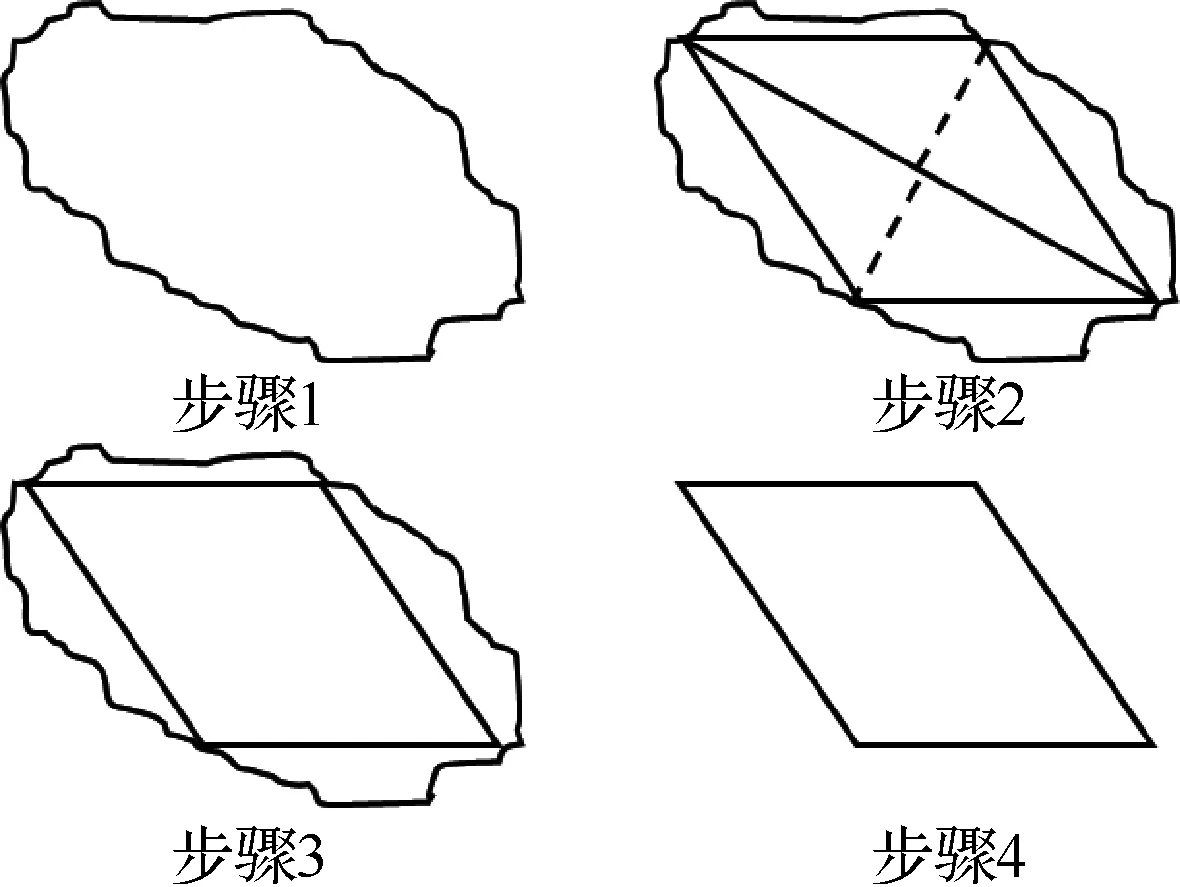
图3 改进Douglas-Peucker过程[10]
最终通过选择合适的误差区间,得到压缩后的复杂地块轮廓图,并运用到接下来的地块凸划分优化中。
1.2 复杂地块中复杂障碍物轮廓近似压缩
不仅复杂地块会对覆盖路径的生成增加难度,复杂障碍物也会使得覆盖路径规划较为困难,故首先要将这些图形转化为凸包。要在原有的复杂障碍物基础上构建凸集,即任意两点的连线都是这个集合内的子集。采用描绘出障碍物轮廓关键点,通过在障碍物轮廓上均匀取样,从而得到原始点集,并根据内折现象的增加适当增加采样点,规定每增加一个内折数nf,采样点数nc增加值为nz,故此时的采样点数为
nc=nz·nf+nc0
(1)
式中:初始采样点数nc0=50;增加值nz=10,从而达到复杂障碍物的所有点连线都在构建的凸集内。得到边缘采样点后,引入平面点集的凸包算法。该方法为经典的卷包裹算法,卷包裹算法是从1个必然在凸包上的点开始向着1个方向依次选择最外侧的点,当回到最初的点时,所选出的点集就是所要求的凸包,这里卷包裹算法的步骤如图4所示,具体为
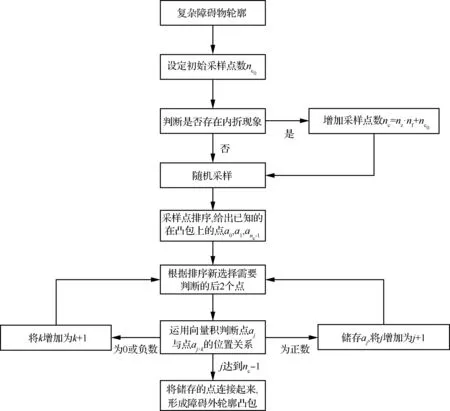
图4 复杂障碍物轮廓采用改进卷包裹算法的流程
1) 得到采样后获得的原始点集,处理的第1步就是将其中的nc个采样点进行排序,首先选择横坐标最小同时纵坐标最小的点,记为a0点,连接该点与其他所有点组成nc-1个向量。计算每个向量与y轴的负半轴之间的夹角,并按照夹角由小到大对所有点进行排序并标记,当存在方向相同的向量则根据模的大小进行排序,最终nc个点分别记作a1,a2,…,anc-1。
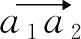
(2)

根据以上步骤得到的凸包边缘点,按照顺序连接线段,即可组成点集的二维凸包,如图5所示。

图5 具体地图(颐和园)实现改进卷包裹算法得到凸包
求解过程中卷包裹算法的复杂度是O(nc·nh),nc是全部的采样点数,nh是最终在凸包上的点数,算法的复杂度会随着内折数nf增大而增大。
2 凹凸顶点定义和凹凸顶点检验
在得到了近似压缩的凹凸顶点后,凹凸顶点对于全覆盖路径规划有着不一样的影响,需要对各个顶点凹凸性进行广义的定义。在最外轮廓中,定义外轮廓中的顶点构成的矩阵为V=[VcVcc],假设多边形外顶点Vc=[v1v2…vi],多边形中外凹顶点Vcc=[vi+1vi+2…vi+j],其中i-2>j。而障碍物轮廓构成矩阵为Vh=[VhcVhcc],假设障碍物的多边形内顶点为Vhc=[vh1vh2…vhm];障碍物多边形中内凹顶点为Vhcc=[vhm+1vhm+2…vhm+n]。且假设多边形外顶点数量远大于内部障碍物多边形内顶点数量,整体凸划分过程中不存在边界宽度的问题。定义了广义的凹凸性顶点,此时就要利用凹凸性检验来验明顶点的凹凸性。
为了将得到的边界和障碍物进行有效地凸划分,此时需要对所有顶点的凸凹性进行检验,利用以当前顶点为中心的矢量叉乘或者计算三角形的有符号面积,判断多边形的方向以及当前顶点的凹凸性。顶点中心矢量叉乘运算,也就是计算三角形面积,当三角形面积为正时,该顶点为凸顶点;同理,当三角形面积为负时,该顶点为凹顶点。
3 针对近似压缩后复杂凹多边形地块的凸划分优化
3.1 含有障碍物的地块凸划分优化
含有障碍物将会大大增加覆盖路径优化的难度,为了方便覆盖路径规划以及减少路径转弯次数,需要采用凸划分的方式优化地块,进而达到优化覆盖路径的目的。
首先,考虑一般情况下,地块边缘都为凸多边形,将内顶点理解成伪凹顶点,根据不同的划分,将地块凸划分的过程复杂度表示为T(i,0,m,n),且最小宽度计算时间复杂度为O(i·j)。
地块凸划分会涉及到障碍物存在伪凹顶点的情况。主要采用4种策略对目标地块进行凸划分,分别是从伪凹顶点边延伸进行划分、通过伪顶点连接进行划分、通过画穿过伪凹顶点的外轮廓划分、以及伪凹顶点和顶点之间连接划分。
对于从伪凹顶点延伸进行划分,若非复杂障碍物情况下,延伸伪凹顶点边可以有效将含有障碍物地块的复杂度降低,此时地块凸划分的过程复杂度为
T(i,0,m,n)≤T(i1,j1,0,0)+T(i2,j2,0,0)+
O((m+1)·i·j)≤T(i,0,0,0)+
T(i,j2,0,0)+O((m+1)·i·j)≤
T(i,0,0,0)+T(i,m-2,0,0)+
O((m+1)·i·(m-2))=C1·i+
O(i2·(m-2)2)+O((m+1)·i·
(m-2))=O(i2·m2)
(3)
式中:C1为计算复杂度系数。
3.2 含有复杂障碍物的复杂地块凸划分优化
前人研究表明,凹多边形会使得覆盖路径的主线受到拦截,从而降低覆盖路径的效率[22]。在算力充裕的情况下,对含有障碍物的复杂凹多边形凸划分可以使得后期覆盖路径规划算法效率更高。凸划分就是将可能影响覆盖路径规划算法的凹顶点划分为子地块,使得总覆盖路径长度更短。如图6所示,在复杂凸多边形中,主要基于4种凸划分策略,优化全地块覆盖路径分配问题。
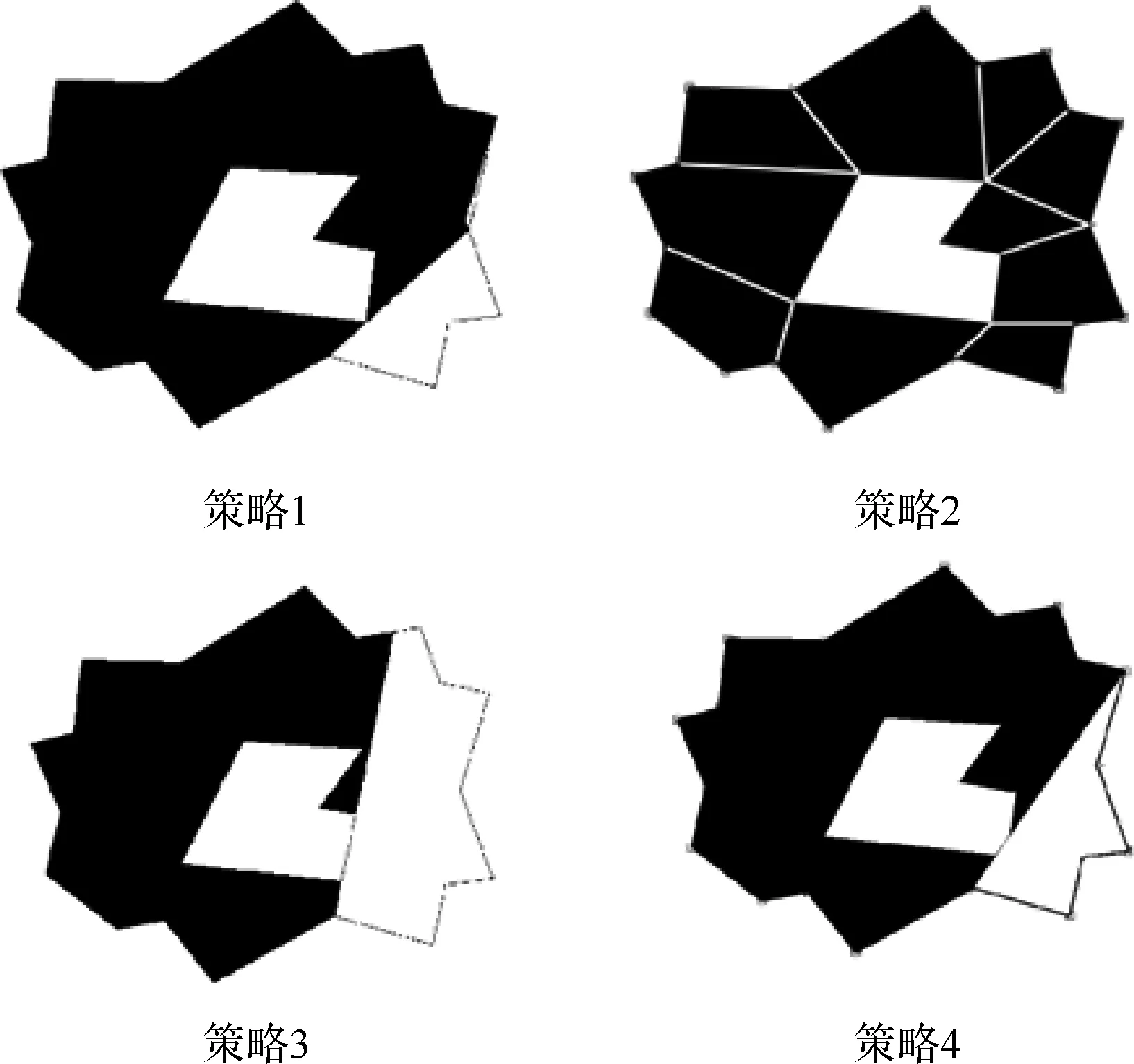
图6 4种凸划分策略示意图
3.2.1 从凹顶点的1个边缘延伸
凸划分的目标是将凹顶点进行分解,由于划分凹顶点时尽量保证某一凹顶点分解为1条外轮廓边与1个凸顶点,从而降低覆盖路径的转弯次数。而对于存在j个凹顶点的含障碍物的子地块,则有2j种划分方式,此时最复杂情况为分解出包含有障碍物的子地块,此时凸划分过程复杂度为
T(i,j,m,n)≤T(i1,0,m,n)+
O(i3·m3+i·j2)
(4)
根据复杂度分析得到凹顶点和凸顶点的数量,直接决定了算法的复杂度,且划分后需要根据划分线DL是否穿过障碍物,分析划分的效果。凸划分算法策略1具体伪代码如算法1所示。
3.2.2 内顶点与外顶点连接划分
伪凹顶点与凹顶点是引起覆盖路径转弯次数较多的主要因素,通过凸划分可以减少2种顶点的数量。首先要对伪凹顶点进行连接,保证外凹顶点优先连接,之后是将内顶点全部与外顶点相连接,此时凸划分的复杂度为
(5)

算法1 从凹顶点的边缘延伸Algorithm 1 Extending from an edge of concave vertex
通过连接顶点的划分线不断组合,将原先的块划分成2个封闭区域,从而达到凸划分的目的。且对于各个分解后的地块,覆盖路径最短为各种组合中的最优组合。凸划分算法策略2具体伪代码如算法2所示。

算法2 内外顶点的连接和划分
3.2.3 平行外轮廓边并经过凹顶点实现划分
在凸划分过程中,保证分割后的地块宽度尽可能较小,分割线就要与外轮廓线平行且过凹顶点分割,从而减少凹顶点个数。对于某1个凹顶点,那可以选择的外轮廓边为i+j-2,此时地块划分的复杂度为
T(i,j,m,n)≤T(i1,0,m,n)+
O(i3·m3+i2·j2)
(6)
在给出每个划分线后,需要对于随机选定的地块给出最优的划分方式。凸划分算法策略3具体伪代码如算法3所示。

算法3 平行外轮廓边并通过凹顶点划分
3.2.4 连接外凹顶点与其他外顶点实现划分
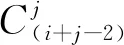
T(i,j,m,n)≤T(i1,0,m,n)+
(7)
通过凸划分整体地块,可以得到较好的划分方式。凸划分算法策略4具体伪代码如算法4所示。

算法4 连接凹的顶点和顶点实现分割
4 凸划分优化与随机路标法融合进行全覆盖路径规划
无人机在进行覆盖作业时,直线飞行可以提高覆盖路径效率,减少重复覆盖,故需要选择平行的1组路线作为主线,而当主线与地块轮廓发生碰撞,则被截断,形成节点;为了将主线连接起来形成完整的覆盖路径,则需要一些辅助路线将路径连接起来,称为辅线。
首先,在含有障碍物的地块中,可以用1个像素矩阵M代表需要覆盖的区域,而通过前期对于图像的处理以及存在障碍物的假设,可以对覆盖区域每个Mij进行一定的定义:
i=1,2,…,p1;j=1,2,…,p2
(8)
此时处理好的目标地块为含有p1个横向像素、p2个纵向像素的像素矩阵。
其次,覆盖路径中主线显然决定了覆盖路径算法的效率,在不同的地块中,对于含有障碍物的地块,为了保证整体路径相对最短,需要确定出最短的覆盖路径算法,故需要对主线进行旋转,寻找最短的主线长度。为了根据给定地块选择合理的主线方向,定义主线及其方向公式如下:
(9)
式中:α表示主线与水平线所成的角度;q1=1,2,…,p2,q2=1,2,…,p1,Lz1、Lz2分别是像素点的横纵坐标值。通过调整主线角度α,可以得到对应的覆盖路径主线最优值。
对于覆盖路径,需要有一定的约束条件,保证路径与障碍物不重合,而此时轨迹的长短与轨迹所在的矩阵点可以表示为
(10)
式中:G为主线集;SL为主线轨迹长度,Pij为落在主线上的可行像素点。由式(10),可得到最优主线角度及此时主线的总长度。
之后需要通过随机路标法确定辅线,首先构建一个含有主线节点的节点概率图,定义节点集V公式:
V={i,j|i=1,2,…,nLz;j=1,2,…,nLr}
(11)
式中:nLz表示主线数量;nLr表示辅线数量,并且对于避障边界B定义如下:
B(i,j,k,p,r,l)=

(12)
在节点集V中,要求节点和节点相互连接,所有的主线都通过辅线连接起来。为了缩短整体路径长度,定义节点距离函数:
(13)
式中:距离D代表的是节点i与节点j的欧几里德距离。通过以上方法,可得到无人机完整的覆盖路径。
在凸划分的基础上,将覆盖路径分为主线和辅线。首先通过不断旋转主线角度确定主线的最短长度,再构建节点概率图,对覆盖路径碰撞边界进行约束;再比较节点间距离,最终查询出相对最短距离,从而得到辅线,结合主线构建出完整的无人机覆盖路径,将凸划分子地块的覆盖路径长度相叠加,并给出最短路径长度的凸划分策略。
5 算法验证
首先随机选择目标地块,由于复杂地块无法进行凸划分优化,故对压缩近似前地块不进行仿真实验。为了验证本文提出的算法的适用性,需要选择合适的地块进行算法验证。由4种凸划分复杂度可以得到,随着i、j、m和n越大,地块凸划分复杂度越大,故本文随机生成含有数量较多的外多边形顶点的复杂地块与含有数量较多的内凹多边形的复杂障碍物,用于验证本文方法的适用性。分别选定1个随机生成的含有复杂障碍物的复杂边界圆整地块,1个随机生成的含有复杂障碍物的复杂长条状地块,以及1个从文献[15]中通过变换得到的对比地图。运行实验采用处理器为Intel(R)Core(TM)i7-6500U CPU,内存为RAM 12.0 GB,使用编程软件及版本为MATLAB 2021a。
算例1对于含有复杂障碍物的复杂边界地块,此时需要通过2架无人机对该地块进行覆盖,地块为随机复杂轮廓地块经过轮廓近似压缩得到的多边形地块,外边界为十九边形,障碍物为六边形,根据之前计算的算法复杂度,该地块的复杂度为T(10,9,6,1),且具备较多的凹顶点与伪凹顶点,有较高的代表性,该区域的顶点坐标为
(14)
为验证凸划分优化的优越性和适用性,首先仿真出该算例地块形状,并验证各顶点凹凸性,如图7所示。其次,需要将没有进行凸划分优化的结果进行仿真,首先进行凹凸点判断,如图8所示。接下来作为对比验证,记录此时覆盖路径长度以及算法规划时间。此时覆盖宽度为40 m,运行结果如图9与表1所示。最后,分别运用4种凸划分优化并结合随机路标法,记录下划分最优时的路径长度与算法规划时间,覆盖宽度统一为40 m,运行结果如图10与表1所示。
表1中策略分别为单纯使用随机路标法(PRM),随机路标法结合策略1(PRM*CD.1)、策略2(PRM*CD.2)、策略3(PRM*CD.3)、策略4(PRM*CD.4)以及凸划分策略中路径长度最短的策略(PRM*CD)所对应的结果,并将各策略的路径长度与算法规划时间绘制成如图11所示。

图7 算例1目标地块

图8 多边形凹凸顶点检验

图9 算例1不采用凸划分优化的结果
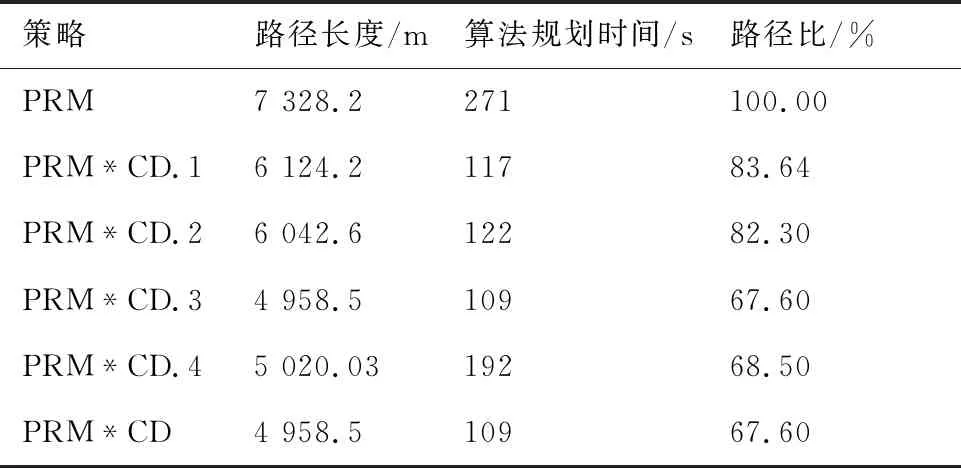
表1 算例1采用4种凸划分策略的优化程度(算法规划时间不包含实时优化时间)

图10 算例1采用凸划分优化的效果

图11 算例1采用凸划分策略覆盖路径长度与算法优化时间对比
通过仿真结果可以看出,凸划分优化策略3得到了较好的优化效果,大大减少了路径长度以及算法规划时间,在覆盖率相同的情况下,整体覆盖路径长度同比缩短32.40%,证明了该方法的优越性,且该地块的复杂程度较大,也可证明本文提出的算法的有效性。
算例2由于算例1中地块采用的是较为圆整的地块,在现实环境中存在长条形地块,故随机给出长条形复杂地块轮廓,经过近似压缩可以得到,外轮廓为八边形,内轮廓为五边形的复杂多边形地块,并且通过凸划分策略实现2架无人机覆盖路径规划,该地块的凸划分复杂度为T(6,2,4,1),有较高的代表性和复杂度,能够代表长条形复杂地块,该区域近似后顶点坐标为为验证算法的有效性,将近似压缩后的多边形地块,仿真出该算例地块形状,并验证各顶点凹凸性,如图12所示。
(15)
将没有进行凸划分优化的情况进行仿真,作为对比验证,记录此时覆盖路径长度以及算法规划时间。此时覆盖宽度为20 m,运行结果如图13与表2所示。
分别运用4种凸划分优化并结合随机路标法,记录下划分最优时的路径长度与算法规划时间。覆盖宽度统一为20 m,运行结果如图14与表2所示。表中策略分别为单纯使用随机路标法(PRM)、随机路标法结合策略1(PRM*CD.1)、策略2(PRM*CD.2)、策略3(PRM*CD.3)、策略4(PRM*CD.4)以及凸划分策略中路径长度最短的策略(PRM*CD)所对应的结果,并将各策略的路径长度与算法规划时间绘制成如图15所示。

图12 算例2目标地块

图13 算例2不采用凸划分优化的结果
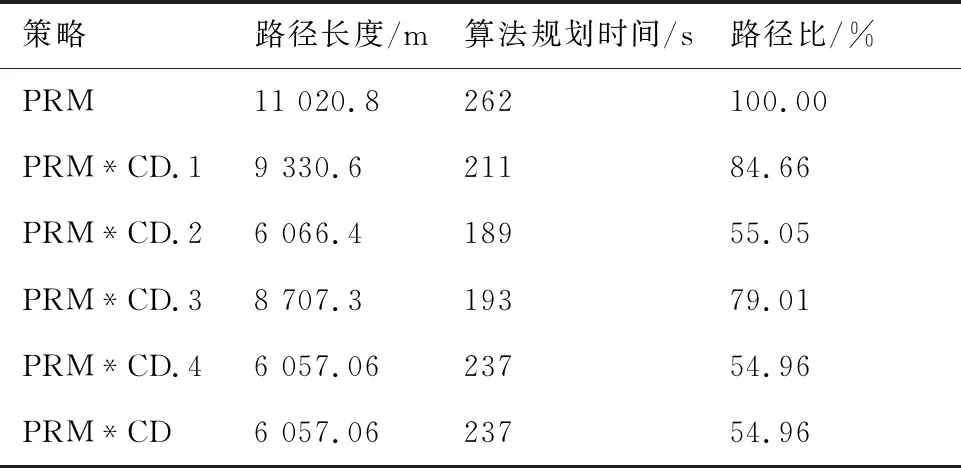
表2 算例2采用4种凸划分策略的优化程度(算法规划时间不包含实时优化时间)

图14 算例2采用凸划分优化的效果
通过以上的仿真结果可以看出,凸划分优化策略4得到了较好的优化效果,大大减少了路径长度以及算法规划时间,在覆盖率相同的情况下,整体覆盖路径长度同比缩短45.04%,证明了该方法的优越性,且该地块属于长条形地块,地块划分复杂性较高,可以较好地证明本文方法的有效性。
算例3由于目前凸划分用于含有障碍物的地块的研究较少,为与现有已知方法进行比较,根据文献[16]中所对比方法的地块,此时需要通过2架无人机对该地块进行覆盖,外边界为十边形,障碍物为七边形,该地块的复杂度为T(8,1,5,2),且有较多文献使用该地块进行算法分析,有较好的普适性,该区域的顶点坐标为为验证算法的优越性,与算例1相似,首先仿真出该算例地块形状,并验证各顶点凹凸性,如图16所示。其次,为比较文中凸划分算法的优越性,将近年的凸划分优化算法与本文中的凸划分优化算法进行比较,并记录覆盖路径长度与算法规划时间,具体仿真结果如图17与表3所示。表中策略分别为单纯使用细胞分解法(Boustrophedon Cellular Decomposition Coverage, BCDC)、随机路标法(PRM)、随机路标法结合文献[16]的延伸法(PRM*IEE(Interior Extension of Edges))、随机路标法结合凸划分策略中路径长度最短的策略(PRM*CD)所对应的结果,并将各策略的路径长度与算法规划时间绘制成如图18所示。
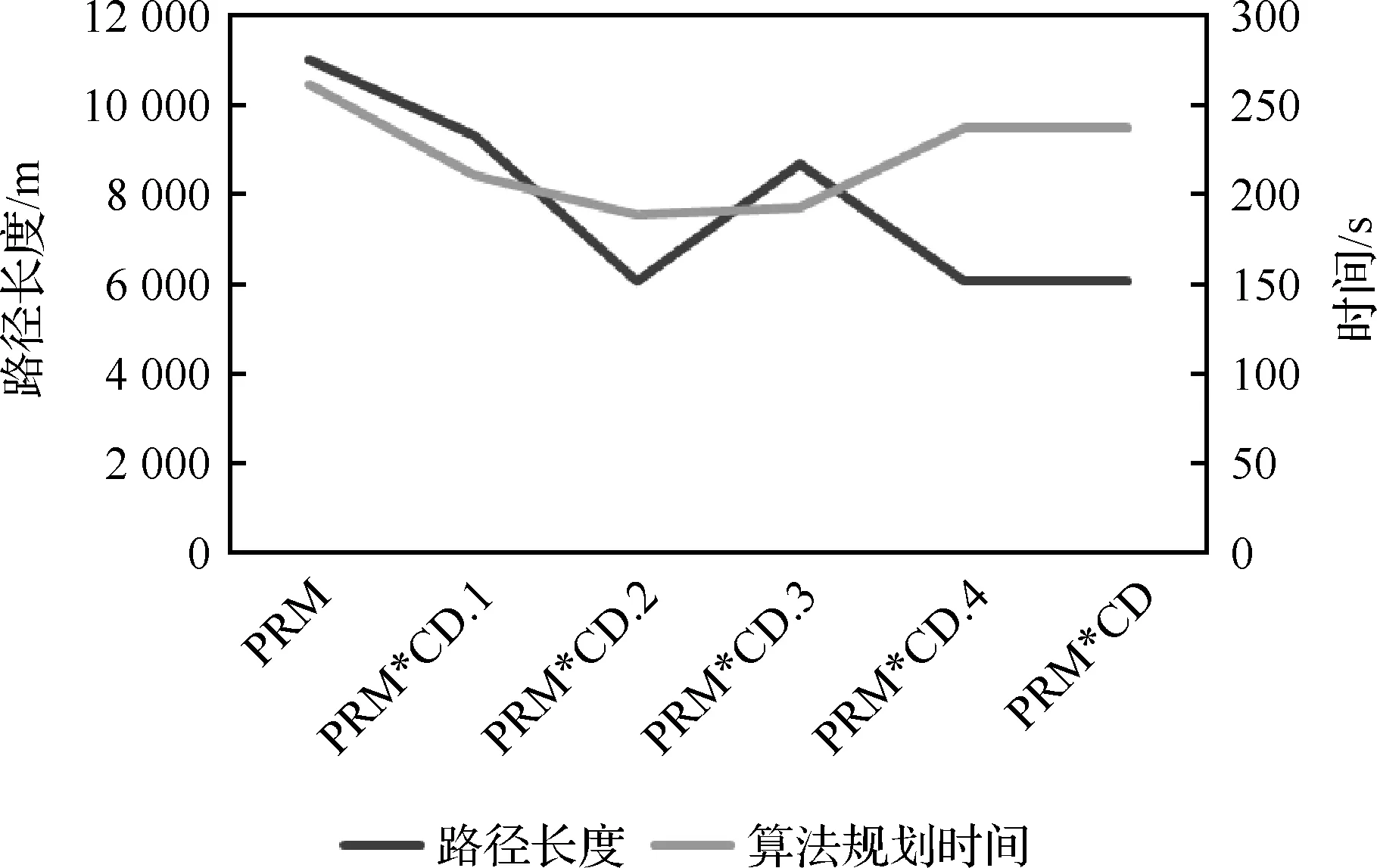
图15 算例2采用凸划分策略覆盖路径长度与算法优化时间对比
(16)

图16 算例3目标地块

图17 算例3采用不同凸划分方法的效果

表3 算例3中不同凸划分方法覆盖路径优化程度对比(算法规划时间不包含实时优化时间)
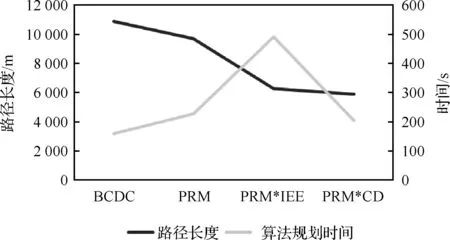
图18 算例3采用不同凸划分方法覆盖路径长度与算法优化时间对比
由仿真结果可以分析出在该地块中,凸划分策略3与随机路标法融合后可以得到最优的路径长度,且通过本文方法的优化后,减少了2个伪凹顶点。通过图18的对比可以得出,对于相同的地块,本文的凸划分优化算法在划分次数较少的情况下,依然减少了3.17%的覆盖路径长度,能够较好地适应复杂地块的覆盖路径规划问题,可以证明本文算法的优越性和有效性。
7 结论与展望
针对凸划分优化以及全覆盖路径规划问题进行了研究,得出如下结论:
1) 针对复杂地块轮廓以及复杂障碍物轮廓进行不同的处理,将复杂地块轮廓进行压缩近似,将复杂障碍物轮廓进行凸包处理,并进行凹凸点检测,可得到易进行凸划分优化的地块轮廓;
2) 提出了4种策略融合随机路标法解决复杂地块含复杂障碍物的覆盖路径规划问题,通过对比其他凸划分算法,可以得到本文的算法对覆盖路径规划有较好的优化效果,减少了覆盖路径长度与算法规划时间,并可以适应更复杂的地块,对随机圆整复杂地块优化路径同比缩短 32.40%,对随机长条形复杂地块优化路径同比缩短45.04%,有较好的推广性,在与其他方法相同地块的对比中也能达到相对最优,可以推广至各种地面机器人、地面无人系统。
未来的研究工作将聚焦于所提出的覆盖路径规划算法运用到遥感无人机的路径规划问题中,提高遥感作业效率,并进一步探究考虑最小转弯半径的无人机覆盖路径规划方法,有针对性地研究4种凸划分优化策略,使其适合优化多种凹顶点分布位置的复杂地块覆盖路径规划问题。

