基于三阶剪切计算连续性方法的编织复合材料板三尺度分析模型
万傲霜, 王振名,李顶河
中国民航大学 航空工程学院,天津 300300
与传统的多向层合复合材料相比,编织复合材料具有优良的面外性能,在航空航天、汽车和船舶等领域的应用日益广泛[1-2]。美国航空航天局于1988年启动先进复合材料技术(ACT)计划,将编织复合材料应用于飞机结构(见图1)[3-4]。编织复合材料也被大量应用于直升机,包括机身蒙皮、主旋翼桨叶、尾梁和尾桨等[5]。
编织复合材料性能不仅取决于组分材料的力学性能和纤维体积分数,还取决于介观尺度上编织纤维束的几何构型,需要采用介观力学方法精确模拟计算编织复合材料的力学响应,这对计算能力提出了很高的要求。为了兼顾计算成本和计算精度,基于均匀化方法的复合材料多尺度分析得到了大量研究。Terada和Kikuchi[6]、Matsui等[7]采用相关变分表述,将均质材料的两尺度建模方法用于具有精细周期性微观结构的非均质材料。Smit等[8]提出了一种在宏观/微观尺度上均考虑材料黏弹性和大变形的均匀化方法。Feyel和Chaboche[9]采用多级有限元方法建立了新的复合材料多尺度模型,考虑了纤维和基体力学性能之间的差异。基于渐近均匀化理论[10-11],Ghosh等[12]建立了非均质材料(包括多孔材料和复合材料)的多尺度弹塑性分析的有限元模型。Miehe[13]基于精细尺度的位移场结果,分析了微观结构线性位移、周期性波动和边界常应力的全局变分问题。Cao[14]计算得到了复合材料弹性静力学问题解的迭代两尺度渐近展开式。Zhang等[15]利用多尺度有限元方法,建立了宏观尺度位移与微观尺度应力应变之间的关系。袁欣和孙慧玉[16]利用均匀化方法计算分析了三维编织复合材料在不同温度下的恒温松弛模量,并进一步建立了由恒温松弛模量确定变温松弛模量的一般方法。杨强等[17]基于多尺度渐进展开理论,对复合材料弹性问题控制方程进行尺度分解,建立了复合材料宏观和细观尺度响应之间的关联。胡殿印等[18]采用通用单胞(GMC)方法,建立了平纹编织复合材料的宏细观多尺度模型,通过与传统有限元单胞模型的宏细观力学响应分析计算结果对比,验证了模型的正确性。

图1 编织复合材料飞机结构件[3-4]
现有的均匀化方法研究大多集中于一阶均匀化理论,该理论假设施加于计算胞元(CUC)或代表性体积元(RVE)的宏观尺度变形梯度是常值,导致大尺寸CUC或大应变梯度情况下的数值模拟结果不够理想。为了捕捉复合材料场梯度和微观结构引起的局部效应,通过引入适当的高阶校正量,进一步发展了二阶均匀化理论,假设宏观变形梯度在CUC求解域上线性变化[19-23]。
由于上述两尺度分析方法难以捕捉编织复合材料这种具有复杂内部结构的复合材料在各尺度上的大量振荡信息,有必要对编织复合材料进行三尺度分析,包括对纤维和基体的微观尺度分析、对纤维束和基体的介观尺度分析、对复合材料结构的宏观尺度分析,大量学者对此开展了研究。Trucu等[24]、Abdulle和Bai[25]系统研究了采用不同偏微分方程三尺度问题的计算收敛性。Ma等[26]采用两尺度渐近展开方法,得到了介观尺度问题的特征函数和特征值,并进一步推导了均匀化单元函数,建立了3个尺度下均匀化系数和材料系数之间的关系。基于均匀化理论和多尺度渐近展开方法,Yang等[27-31]提出了一种研究非均质材料在微观、介观和宏观尺度上耦合传导辐射和热力学问题的高阶三尺度分析方法。但是,这种方法必须结合高阶单元解和一致解来构造三尺度渐近解,限制了该方法的应用。
为了克服均匀化理论和广义连续理论的局限性,文献[32-35]提出了计算连续性(C2)方法,可以对有限大小非均质体进行粗尺度连续性描述,该方法的粗尺度控制方程在不相交胞元组成的计算连续域上表示,确定了胞元位置后,在细尺度上确定控制方程的弱形式。这种不进行尺度分离的多尺度分析方法可以在不假设细尺度胞元无限小的条件下提供细尺度信息,并且不需要高阶连续性、高阶边界条件和引入新的自由度。最近,C2方法被应用于等效单层理论框架下的复合材料层合板多尺度分析[36-37]以及三阶剪切变形理论(TSDT)框架下的混凝土结构和复合材料曲梁多尺度分析[38-40]。
因此考虑到编织复合材料的宏观力学性能取决于细观组分材料性能和介观纤维束编织构型,为了在可接受的计算成本下准确计算编织复合材料的位移场和应力场,有必要建立三尺度有限元模型。因此,本文提出一种基于三阶剪切计算连续性方法的编织复合材料板三尺度分析模型。采用基于TSDT的八节点四边形板单元对宏观尺度模型进行离散,推导三尺度三阶剪切计算连续性(TOS-C2)方法及其有限元方程;构建编织复合材料板三尺度TOS-C2方法的计算框架,利用含夹杂三维立方体的数值算例,检验该方法的有效性;利用三尺度TOS-C2方法,模拟计算平面编织复合材料板的微观、介观、宏观尺度位移场和应力场。
1 理论模型
1.1 三阶剪切变形理论
首先三阶剪切变形理论的位移假设为
(1)
其中:
(2)
式中:(x,y,z)为板上某一点的坐标;h为板的厚度;u0、v0、w0分别为中心面上一点(x,y)在x、y、z方向的位移;u1、v1分别为(x,y)的剪切转角;∂w/∂x、∂w/∂y分别为(x,y)的弯曲转角。根据位移假设,应变分量可推导为
(3)
其中:
(4)
由式(3)可以看出,横向剪切应变沿板厚呈抛物线变化,并在板的上表面和下表面达到0,不需要使用剪切校正因子。外载荷的应变能和外力功可表示为
(5)
其中:
(6)
式中:C为刚度矩阵;A为面积;w为位移;εx、εy、εxy、εyz、εxz为应变分量;σx、σy、σxy、σyz、σxz为应力分量;q为面积力。式(5)为推导有限元方程的基础。
层合板的本构关系为
(7)
式中:Cij为刚度系数。

(8)


图2 八节点四边形板单元(坐标系原点位于板单元中心面上)
根据式(3),应变-位移的关系可写为
(9)
式中:εp和εt分别为面内应变和弯曲应变;Lp和Lt分别为面内应变和弯曲应变的位移关系矩阵。
任意一点的位移矢量u可表示为
u=Nde
(10)
式中:[N]5×48为形函数矩阵,下标表示该矩阵的维度,具体表达式见附录A;节点位移矢量[de]48×1为
(11)
式中:上标(i)为节点编号。
那么,面内应变和弯曲应变可以用节点位移矢量来表示
(12)
式中:Bp和Bt分别面内和弯曲为应变-位移矩阵,表达式为
(13)
总应变可写为
(14)
[Bp]3×48、[Bt]2×48、应变-位移矩阵[B]5×48的表达式见附录A。
1.2 三尺度计算连续性方法
基于C2多尺度方法的位移和应变分解,三尺度计算连续性模型的位移场和应变场分别可表示为
(15)
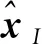
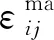
(16)
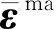
α,β,…,δ=1,2,3
(17)
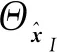
1.3 有限元方程
1.3.1 微观尺度
由单丝纤维和基体组成的微观尺度问题的弱形式定义为

(18)
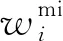
将微观权函数umi和试探函数wmi用形函数Nmi(ψ)进行离散:
(19)
式中:dmi、cmi分别为权函数和试探函数的节点值。
将式(14)~式(16)、式(19)代入微观尺度胞元问题的弱形式中,并且考虑到试探函数cmi的任意性,微观尺度胞元问题权函数在节点处解的表达式为
(20)
式(20)可以简写为
(21)
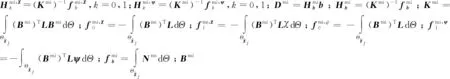
1.3.2 介观尺度
由纤维束和基体组成的介观尺度问题的弱形式定义为
(22)
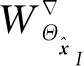
同样地,将介观权函数ume和试探函数wme用形函数Nme(χ)进行离散,表达式为
(23)
式中:dme、cme分别为权函数、试探函数的节点值。根据介观应变的泰勒展开式,用权函数和试探函数对其进行表示为
(24)
其中:
α=1,2,3
(25)
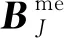
将式(16)、式(21)、式(24)代入介观尺度胞元问题的弱形式中,并且考虑到试探函数cme的任意性,介观尺度胞元问题权函数在节点处解的表达式为
(26)
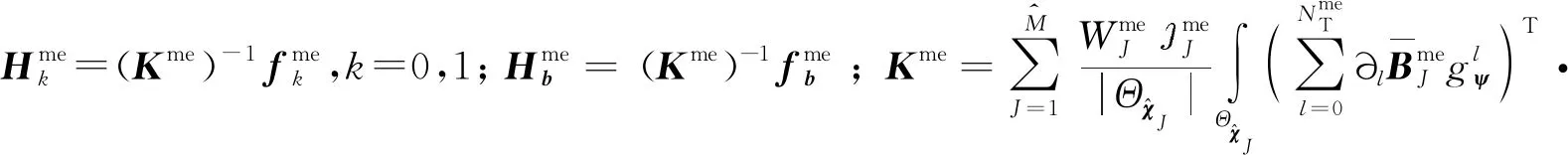
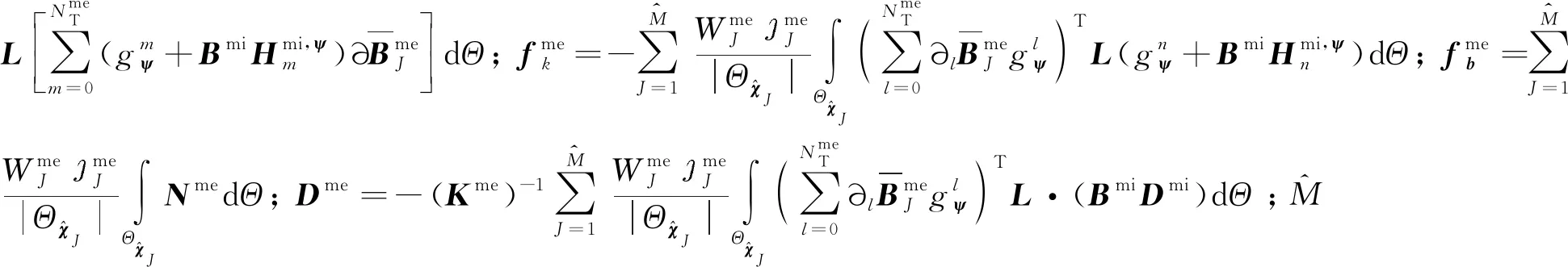
1.3.3 宏观尺度
宏观尺度问题的弱形式可定义为
∀wma∈WΩx
(27)
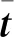
同样地,将宏观权函数uma和试探函数wma用形函数Nma(χ)进行离散,表达式为
(28)
式中:dma、cma分别为权函数和试探函数的节点值。根据宏观应变的泰勒展开式,用权函数和试探函数对其进行表示为
(29)
其中

(30)

式(21)、式(26)可以写为
(31)
(32)
式中:
(33)
将式(31)、式(32)代入宏观尺度问题的弱形式中,并且考虑到试探函数cma的任意性,宏观尺度问题权函数在节点处解的表达式为
dma=(Kma)-1fma
(34)
其中:
(35)
2 计算框架
图3为三尺度三阶剪切计算连续性(TOS-C2)

图3 三尺度TOS-C2方法计算框架
方法的计算框架,具体流程如下:
1) 建立宏观问题、介观胞元和微观胞元的有限元模型。
4) 由宏观尺度模型的有限元方程,计算宏观位移dma(见式(34))。

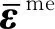
7) 后处理得所需尺度模型位移和应力分布。
基于Microsoft Visual Studio软件,通过编写程序实现上述计算框架。
3 数值算例
3.1 验证算例
利用含夹杂的三维立方体算例来验证所提出的三尺度TOS-C2方法。分别采用直接数值模拟(DNS)方法和三尺度TOS-C2方法建立有限元模型(见图4、图5),并进行对比分析。该验证模型中的夹杂是指弹性模量较高的区域,类似微观尺度上纤维束胞元模型的的单丝纤维。对于三尺度TOS-C2模型,微观尺度胞元如图4(a)所示;图4(b)表示8个微观尺度胞元组成的介观尺度胞元模型夹杂域(见图4(c))中的1个单元;整个介观尺度胞元模型如图4(d)所示。微观和介观尺度胞元模型均采用Hex8单元,其中介观模型中采用非局部积分。由于1个宏观尺度单元由4个介观尺度胞元组成,宏观尺度模型(见图4(e))共包含256个介观尺度胞元,分别在x、y方向有8个单元。对于DNS模型,单元尺寸则由微观夹杂决定,整个DNS模型(见图5(a))由夹杂(见图5(b)、图5(c))和基体组成。夹杂的材料属性取弹性模量E=10.0 GPa,泊松比μ=0.3,基体的材料属性取E=1.0 GPa,μ=0.3。宏观模型的边界条件为
(36)
将由DNS模型和三尺度TOS-C2模型计算得到的应力和位移结果进行对比分析,如图6~图8所示。从图6中可以看出,三尺度TOS-C2模型计算得到的宏观位移结果与DNS模型吻合良好,但宏观应力计算结果存在一定偏差。为了将三尺度TOS-C2模型的介观位移和应力结果与DNS模型进行对比,选取如图4(e)所示一条线上的A、B、C作为分析对象。图7、图8、表1对比了介观尺度胞元模型和DNS模型的位移及应力结果,可以看出2种模型的介观尺度位移计算结果吻合良好,但应力计算结果存在一定偏差。需要指出的是,因为考虑到需要将DNS模型的计算量控制在可求解范围内,网格划分较为稀疏(TOS-C2介观和微观胞元模型分别为3×3×3和9×9×9单元数,而DNS模型中与介观和微观尺度相对应均采用3×3×3单元数),导致应力计算结果与DNS模型存在一定偏差,考虑到位移计算结果吻合良好,认为该模型的计算误差在可接受范围内。DNS模型和三尺度TOS-C2模型的单元数、节点数、计算时间和CPU数量见表2,可以看出三尺度TOS-C2模型在计算效率上有显著优势。此外,三尺度TOS-C2方法不仅可以有效分析含夹杂三维立方体的应力应变响应,由于该方法采用三阶剪切变形理论,不存在剪切闭锁问题,所以也能有效分析编织复合材料板的应力应变响应。
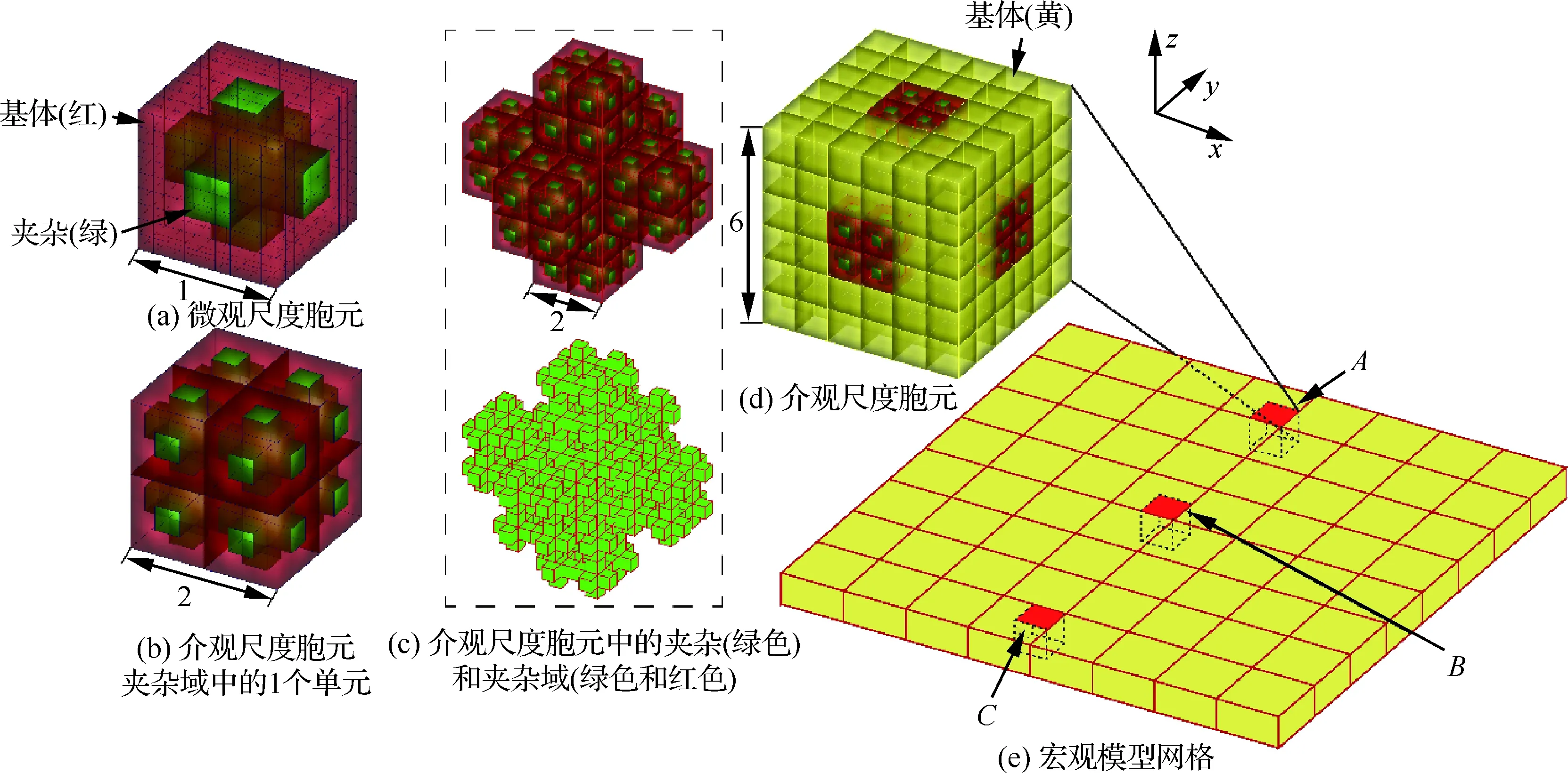
图4 含夹杂三维立方体的三尺度TOS-C2模型

图5 含夹杂三维立方体的DNS模型

图6 含夹杂三维立方体位移和应力计算结果

表1 含夹杂三维立方体A、B、C 3点处DNS模型和TOS-C2介观胞元模型的位移和应力计算结果

表2 含夹杂三维立方体DNS模型和三尺度TOS-C2模型的计算量
3.2 平面编织复合材料板三尺度TOS-C2模型
图9~图11为采用提出的三尺度TOS-C2方法对平面编织复合材料板进行三尺度分析的过程和结果。图9(b)为宏观尺度模型(见图9(a))中第25个单元的第4个积分点对应的介观尺度胞元模型,分为2个部分,即介观基体(见图9(c))和编织纤维束(见图9(d))。图9(e)为放大后的介观尺度纤维束,其中1个单元的求解域包含8个微观尺度胞元(见图9(f)、图9(h)),图9(g)、图9(i)分别为8个微观尺度胞元以及微观尺度胞元中的单丝纤维。该三尺度模型中,介观尺度和微观尺度基体的材料属性都是E=2.1 GPa,μ=0.3,微观模型中单丝纤维的材料属性为E=210 GPa,μ=0.3。宏观尺度模型的边界条件为四边固支,并在底部施加均匀分布载荷p=1 Pa。
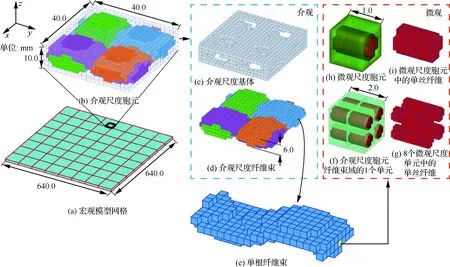
图9 平面编织复合材料板的三尺度TOS-C2模型
图10 平面编织复合材料板三尺度TOS-C2模型的位移计算结果
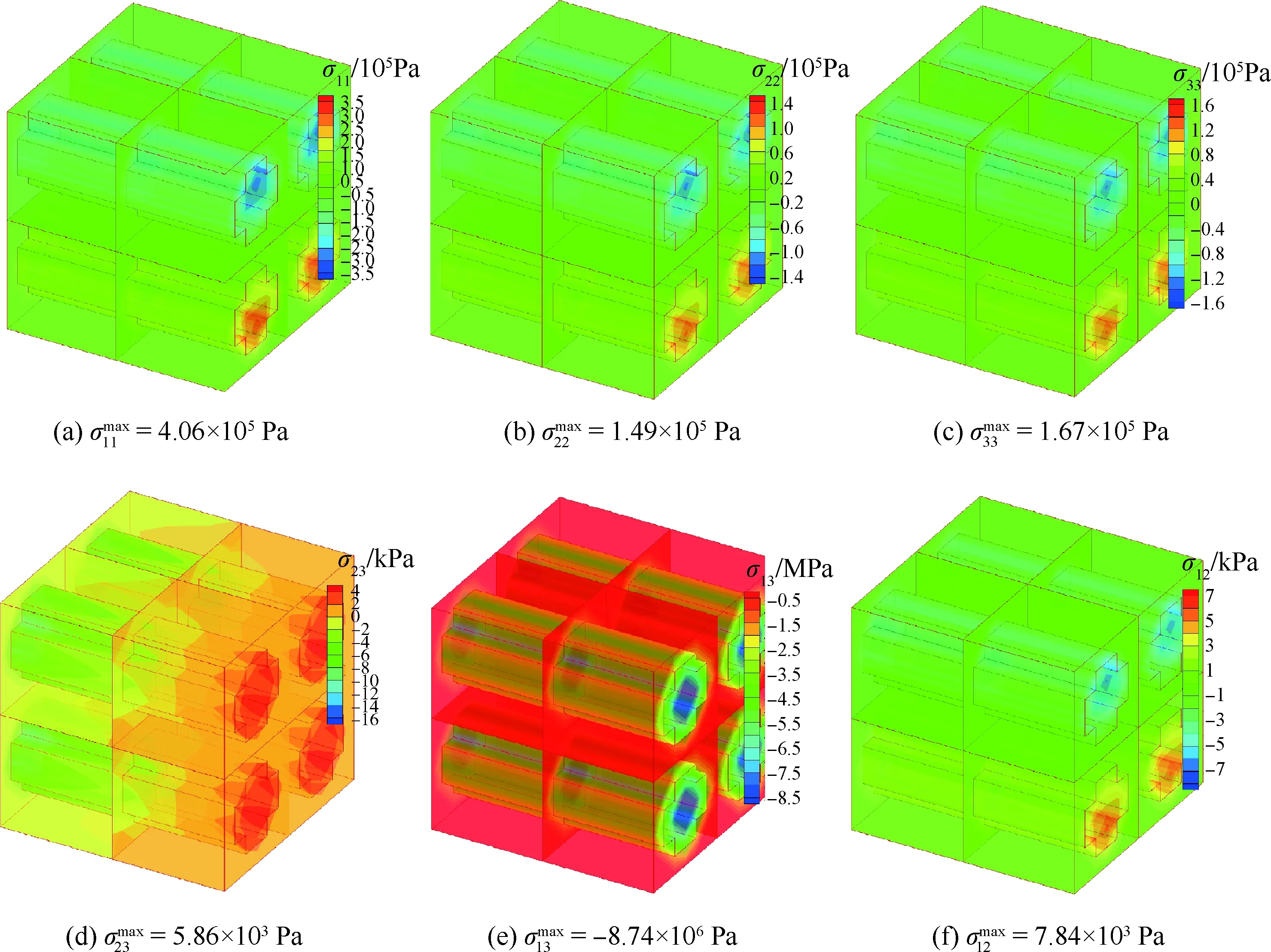
图11 平面编织复合材料板TOS-C2微观模型的应力计算结果
4 结 论
基于三阶剪切变形理论(TSDT)和计算连续性(C2)方法,提出了新的编织复合材料板三尺度分析模型,得到如下主要结论:
1) 采用基于TSDT的八节点四边形板单元对宏观尺度模型进行离散,可以考虑剪切变形和沿厚度方向非线性剪切应变变化引起的转动惯量。
2) 利用含夹杂三维立方体的数值算例,验证了提出的三尺度三阶剪切计算连续性(TOS-C2)方法的有效性,三尺度TOS-C2模型的位移和应力计算结果与直接数值模拟(DNS)模型吻合良好。
3) 提出的三尺度TOS-C2方法可以详细描述编织复合材料板的微观和介观尺度结构以及三尺度位移和应力分布,为编织复合材料板航空航天结构设计和力学性能分析提供技术支持,并且,由于三尺度TOS-C2方法中宏观和介观尺度应变均采用泰勒级数展开,该方法可以适用于应力变化剧烈的复杂单元问题。

