考虑瞬态效应的周期性多材料传热结构拓扑优化
李信卿,赵清海,2,*,龙凯,张洪信
1. 青岛大学 机电工程学院,青岛 266071
2. 青岛大学 电动汽车智能化动力集成技术国家地方联合工程研究中心,青岛 266071
3. 华北电力大学 新能源电力系统国家重点实验室,北京 102206
近年来,具有高效传热性能的周期多材料结构在航空航天、汽车工程等领域应用广泛[1],通过采用不同种导热材料,寻求最佳的传热路径,在实现轻量化设计的同时达到结构的性能最优。因此,考虑周期性约束的多材料传热结构拓扑优化问题逐渐成为当前的研究热点。
自Sigmund等[2-3]首次通过逆均匀化法获得极具力学性能的周期性材料微结构以来,周期结构的拓扑优化研究得到了快速发展,文献[4-7]给出了其在不同发展阶段的研究方法和理论。作为兼具装配简单、易于模块化加工等特征的周期性传热结构,其设计优化具有重要的研究意义和工程价值。贾娇等[8]基于固体各向同性材料惩罚法 (Solid Isotropic Material with Penalization,SIMP)的周期性材料插值模型,验证宏观导热性能的周期性材料设计的有效性。赵清海等[9]探究了周期性约束下结构稳态热传导拓扑优化设计方法。Yan等[10]考虑温度场和流场的周期性,计算了双周期纤维增强复合材料的有效横向导热系数。
以上文献基于稳态热传导控制方程开展研究,然而在实践中导热问题本质上为瞬态状态,热负荷大都具有周期性和短时特征,温度分布随时间和空间变化的瞬态效应明显[11]。目前,考虑瞬态效应对热传导问题影响的周期传热结构拓扑优化研究日益凸显。Turteltaub[12]最先扩展用于瞬态拓扑优化的SIMP方法,实现热柔顺度实际值与期望值之间的差异最小化。此后,均匀化法、水平集法等相继被用于瞬态热传导问题研究[13-14]。Zhuang和Xiong[15]提出全局热柔顺度指标,实现瞬态热传导拓扑优化过程中峰值热柔顺度最小化。Wu等[16-17]引入区域温度控制函数搭建瞬态热传导拓扑优化数学模型,提出一种基于瞬态散热效率的热传导结构拓扑优化方法。上述考虑瞬态效应影响的拓扑优化研究极大推动了时变热负荷下传热结构构型的设计优化,为传热结构在工程上的应用提供了理论支撑。然而受限于材料属性的影响,单材料结构优化往往难以实现性能综合最优。在此背景下,增材制造技术[18]的出现为多材料结构拓扑优化的研究提供了技术支撑。Zuo和Saitou[19]通过引入尺度系数和平移系数,利用归一化密度变量插值多种材料的弹性模量求解多材料拓扑优化问题。龙凯等[20]提出了以结构总重最小化为目标和给定特征值为约束的拓扑优化模型,以实现基于多相材料的结构轻量化设计。Li等[21]针对载荷不确定的功能梯度结构,开展周期性多材料稳健拓扑优化设计。
综上所述,未考虑瞬态效应的周期性传热结构优化存在设计局限性,且研究多以单材料结构为研究对象。因此,本文针对瞬态热传导目标响应最大值最小化问题,建立了基于有序有理近似材料属性法(Ordered Rational Approximation of Material Properties, Ordered-RAMP)的周期性多材料拓扑优化模型。以传热结构最高温度最小化和最高散热耗能最小化为设计目标,直观展现了所提方法的工程应用价值。在此基础上,运用伴随向量法进行灵敏度推导,借助偏微分方程过滤法处理数值不稳定问题,并选取移动渐近线法对设计变量进行迭代更新。最后通过数值算例证明所提方法的有效性。
1 瞬态热传导问题分析
1.1 考虑瞬态效应的多材料传热结构
考虑瞬态效应的传热结构如图1表示。由热源P(t)、空洞、恒温边界Г1、绝热边界Г2以及导热材料Mat-1、Mat-2和 Mat-3组成。
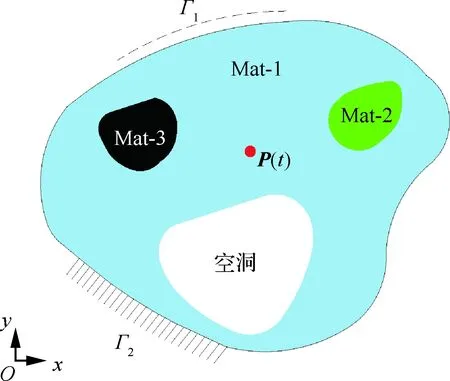
图1 三材料瞬态传热结构
设计域内瞬态热传导的表达式为
(1)

(2)
(3)

1.2 瞬态热传导分析
基于有限元法,二维温度场的瞬态热传导问题控制方程可转化为

(4)
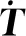
(5)
式中:Δt=tz+1-tz,tz为第z个时刻;Tz和Tz+1分别为第z时刻和第z+1时刻的温度向量,O(Δt)为插值余项。
针对温度场和载荷向量,利用θ-时间差分法[22]求解
Tz+θ=θTz+1+(1-θ)Tz
(6)
Qz+θ=θQz+1+(1-θ)Qz
(7)
式中:θ为算法参数,当θ=0时,为向前差分法;当θ=1,为向后差分法;Qz为第z时刻热负荷向量。
将式(5)~式(7)代入式(4),得到温度离散迭代格式:
(C+θΔtK)Tz+1=[C-(1-θ)ΔtK]Tz+
Δt[θQz+1+(1-θ)Qz]
(8)
2 周期性多材料结构建模方法
2.1 瞬态热传导拓扑优化模型
基于变密度理论,考虑瞬态热传导问题中瞬态响应最大值最小化设计数学模型表示为
(9)
式中:xi为单元相对密度,代表设计变量;Ne为设计区域单元总数;vi为单元体积;ζ和V0分别为设计域的体积比和初始体积;xmax和xmin分别为单元密度的上下限;f(T(t),x)为目标函数。
针对f(T(t),x)展开研究,考虑如下两种设计目标。
目标I节点温度
f(T(t),x)=Ttarget=LTT(t)
(10)
式中:L为列向量,在目标节点处值为1(有可能不止一个目标点),其他为0;Ttarget为目标温度向量。
目标II散热耗能
(11)
2.2 Ordered-RAMP多材料插值模型
RAMP法的数学模型描述如下
(12)
式中:ψ为插值后的热传导系数和热容系数;ψ0为初始热传导和热容系数;β为惩罚因子。
针对多材料传热结构拓扑优化设计,将各导热材料的密度值、热传导系数和热容系数进行归一化处理,变换材料属性的绝对值为无量纲的相对值关系,数学模描述为
(13)

引入比例系数Aψ和平移系数Bψ,构建基于Ordered-RAMP法的多材料插值模型为
(14)
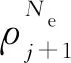
(15)

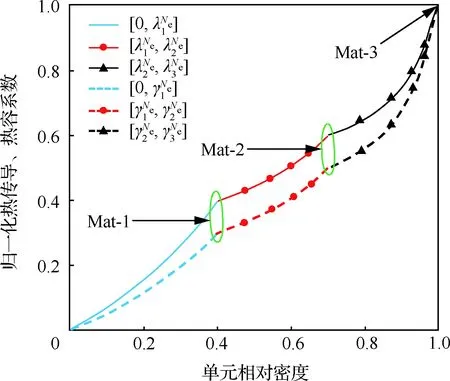
图2 基于Ordered-RAMP的多材料插值模型
定义单元多材料热传导矩阵和热容矩阵为
ki=[λmin+ψλ(λmax-λmin)]k0
(16)
ci=[γmin+ψγ(γmax-γmin)]c0
(17)
式中:k0和c0分别为单元热传导矩阵和单元热容矩阵;ψλ和ψγ分别为插值后的热传导系数和热容系数;ki和ci分别为单元多材料热传导矩阵和热容矩阵;λmin和γmin分别为基板热传导系数和热容系数的最小值。
2.3 灵敏度推导
在瞬态热传导拓扑优化研究中可能存在设计变量的最大瞬态响应不可微的情况[23]。因此,通过引入聚合函数,将原始分析方程在时域离散,之后根据聚合函数的离散形式进行灵敏度分析。借助聚合函数φ代替原目标函数,定义为
(18)
式中:tf为时间分段数;a为常量;当a→+∞时φ→max{f(T(t),x)};f为f(T(t),x)的简写。
引入伴随向量ϑ,构建新的目标函数

(19)
对于任一设计变量xi的灵敏度计算得到
(20)
式中:
(21)
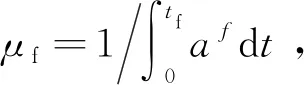

(22)
考虑ϑ|tf=0,则式(22)可简化为

(23)
将式(23)代入式(20)中,得到

(24)
式中:Λ为温度灵敏度项。
不考虑载荷设计相关性影响,为消除温度灵敏度项Λ,可得
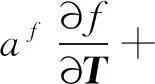
(25)
相应地,目标函数灵敏度方程为

(26)
伴随向量ϑ计算公式为
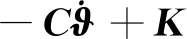
(27)
根据式(16)和式(17),整体热传导和热容刚度矩阵相对于xi的导数为
(28)
(29)
针对两种设计目标函数,导数信息如式(30)和式(31)所示。
目标I节点温度
(30)
目标II散热耗能
(31)
2.4 灵敏度过滤和设计变量更新
针对优化结果中难以避免的棋盘格、网格依赖性、局部极值等数值不稳定现象[24],借助基于Helmholtz方程的偏微分过滤方法[25]处理数值不稳定问题,其过滤方程组为
(32)
(33)
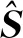
(34)
目前常用的优化求解算法包括数学规划法和优化准则法。移动渐近线法[26](Method of Moving Asymptotes,MMA)在迭代过程中,可用梯度类算法求解优化问题以获取新的设计变量,对具有复杂目标和多约束拓扑优化问题,具有更好的适用性,故选取MMA进行瞬态热传导结构拓扑优化设计求解。
2.5 周期性设置
为了获得考虑瞬态响应的周期性多材料结构拓扑优化形式,使得时间历程下不同子区域在相同位置处的单元具有相同的材料属性。将设计区域划分为Mx×My个相同的子区域,其中Mx和My分别代表x与y轴方向的子区域数。总的时间历程tf,热负荷作用时间为t1,t2,…,tz,…,tf。周期性结构的数学模型可以描述为
(35)
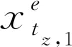
时间历程下通过重新分配过滤后的单元目标函数基值,使子区域上任意单元基值为全部子区域对应单元的平均值,即
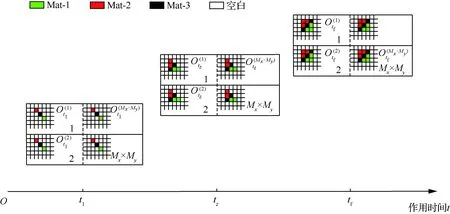
图3 周期性多材料结构示意图

(36)
2.6 算法求解步骤
考虑瞬态效应的影响,基于Ordered-RAMP多材料插值模型,进行传热结构周期性拓扑优化设计研究,具体流程如下。
步骤1定义传热结构设计域、材料属性、边界条件与热负荷工作时间以及周期约束等参数。
步骤2初始化材料设计变量、温度边界和热负荷。通过有限元法离散设计域,获得单元热传导矩阵和热容矩阵。
步骤3计算整体热传导矩阵和热容矩阵。初始化时间变量,并通过向后差分法计算温度场和载荷向量。
步骤4得到瞬态热响应。叠加目标函数,并计算相对于设计变量的导数。
步骤5采用偏微分方程过滤方法进行灵敏度过滤。并进行周期性约束设置。
步骤6借助移动渐近线法对多材料设计变量进行迭代更新,判断优化结果是否收敛,若是,则输出最优拓扑构型;若不是,则返回步骤3,重复上述步骤,直至输出最优结果。
3 数值算例
针对瞬态热传导问题,考虑周期性结构的子区域个数和热负荷工作时间,给出二维和三维3个数值算例。定义传热背景区域的导热系数λmin=1 W/(m·K),热容为γmin=105J/(K·m3)。在区域的中心点施加热源并布置导热材料,最高导热和热容材料的导热系数为100 W/(m·K),热容为106J/(K·m3)。体积分数ζ=0.2,惩罚因子βλ=9、βγ=6。整个时间历程tf,步长Δt=tf/100,参数θ定义为1。
3.1 二维算例1
选取几何尺寸为0.6 mm×0.6 mm×0.01 mm的方形结构,将其离散为180×180个方形单元。设计域如图4所示,在中心点施加强度为P(t)=0.01 W的热源,四角点温度恒为0 ℃,其余边界绝热,总时间历程tf=0.01 s,过滤半径rmin=1.2。选取3种材料进行优化设计,材料参数归一化值如表1所示。
针对不同的设计目标(目标I——节点温度;目标II——散热耗能)进行优化,周期设置Mx×My分别为1×1、3×3与6×6。考虑热负荷作用时间t=0.000 4,0.001 0,0.004 0,0.008 0,0.010 0 s,拓扑优化构型、目标I最高温度Tmax和目标II最高散热耗能Pmax如表2所示。图5为热负荷工作0.001 0 s时,目标I、II在周期设置下目标函数随迭代步数变化曲线。

图4 2D结构设计域
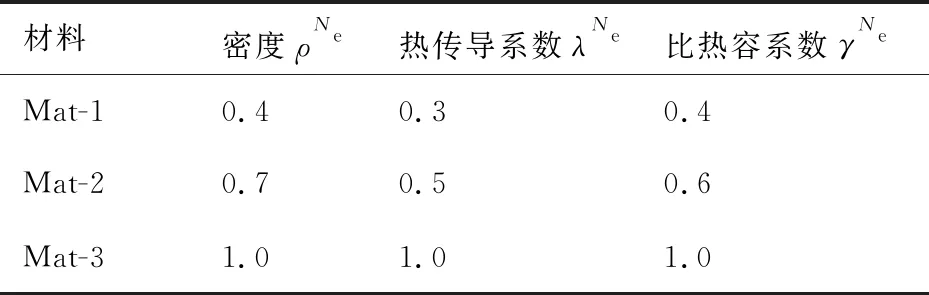
表1 3种材料参数设置
由表2可知,所提方法可实现基于瞬态热传导的周期性传热结构多材料拓扑优化设计。不同热负荷作用时间下所得的拓扑构型有较大差异。当周期为奇数设置时,如1×1、3×3,随着作用时间的增加,结构会呈现×形变化趋势,即从加热中心点向0 ℃温度点延伸的变化,体现出寻求最短散热路径的特点,可以发现加热点为最高温度点。当周期为偶数设置时,如6×6,结构子区域则呈现框形。从材料布局角度看,传热结构呈现由中心位置处导热和热容系数较大材料向四周较小导热和热容系数的材料延伸的分布,这说明所提方法具有处理多材料布局优化的能力。
同时,随着热负荷作用时间和子区域划分个 数的增加,目标I的最高温度和目标II的最高散热耗能都呈现一种逐渐升高的趋势,这同实际物理现象相符。子区域数目增多,其优化自由度会相应地减少,结构散热性能降低,节点温度、散热耗能升高。
周期设置为3×3、加热时间为0.01 s条件下,周期性传热结构的目标函数和子区域随迭代步数的变化如图5所示。迭代过程中,目标函数能快速收敛到最优解且收敛过程中无较明显波动,证明该算法具有较好的稳定性。
3.2 二维算例2
研究了多热源工况对周期性传热结构的宏观构型、子区域构型以及目标性能的影响。定义几何尺寸为10 mm×10 mm×10 mm的四热源传热结构,将其离散为160×160个方形单元,设计域如图6所示。其中红色区域为施加热源,黑色区域为热骨架(即非设计域),该区域在优化结果中显示为白色,单元厚度h=10 mm,边界绝热,总时间历程tf=104s,过滤半径rmin=1.2,材料参数设置同二维算例1(3.1节)。
图7为热源发热功率随时间变化曲线,数学表达式为
(37)
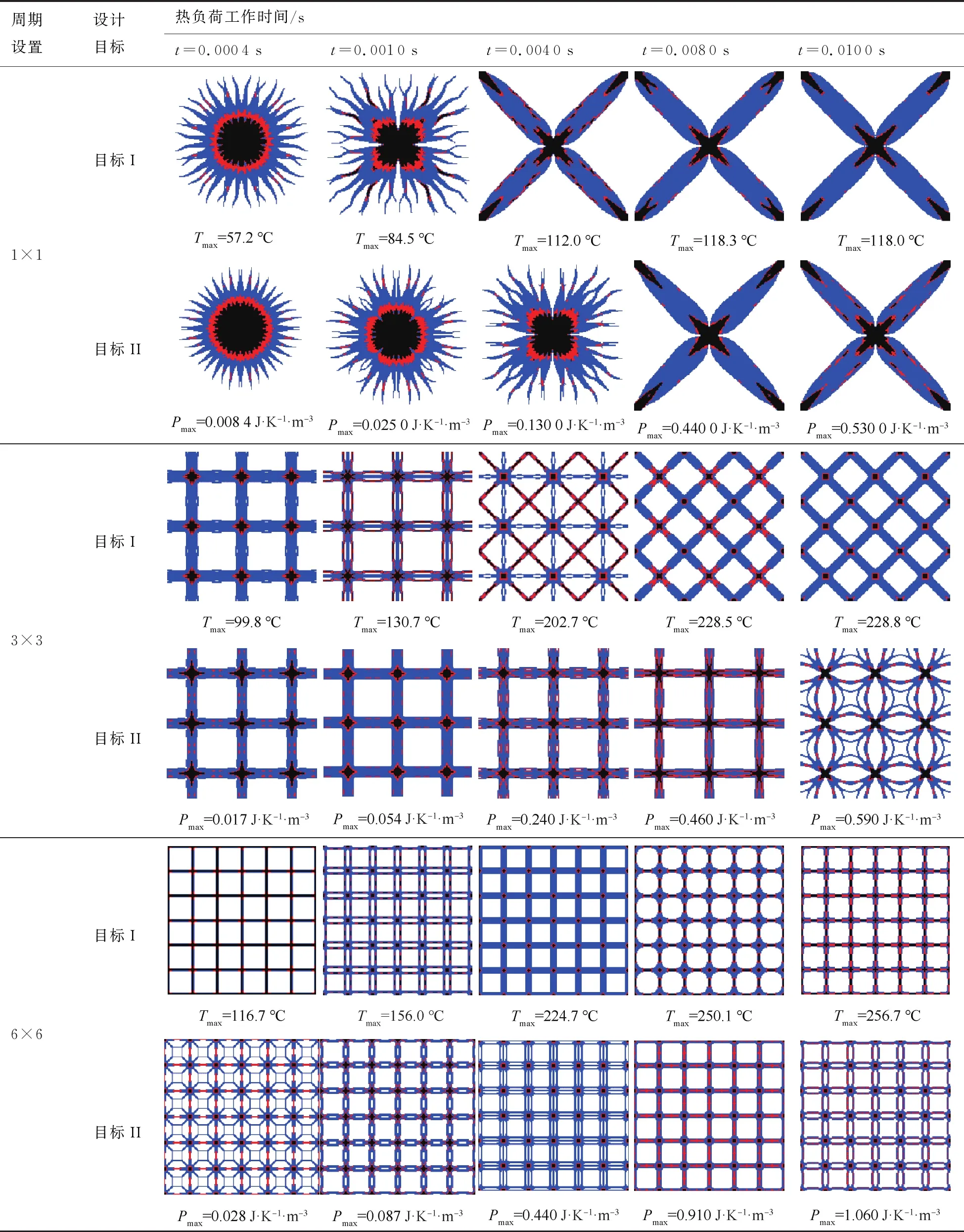
表2 不同热负荷作用时间下的周期性拓扑构型、最高温度和散热耗能值
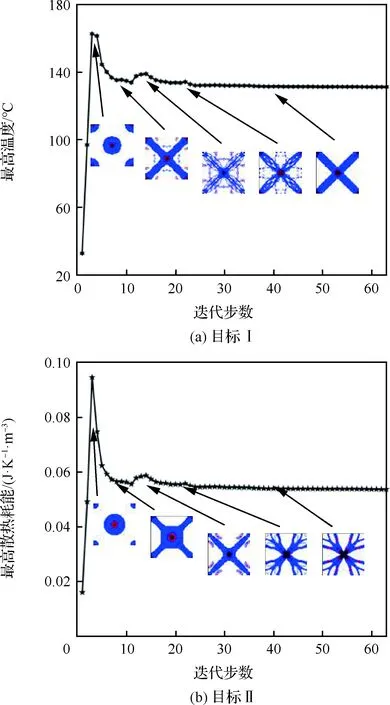
图5 目标函数随迭代步数变化曲线

图6 宏观设计域
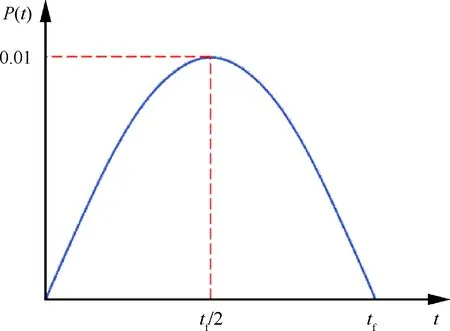
图7 热源发热功率
针对设计目标I和目标II进行优化,周期设置Mx×My分别为1×1、5×5与8×8。考虑两个热负荷作用时间400、5 000 s,周期设置为Mx×My=1×1,即非周期设置时,拓扑优化构型如图8、图9所示。可见不同设计目标下优化构型具有较大差异,材料分布呈现从热骨架所在方形区域向边界扩展的趋势。

图8 目标I非周期优化构型

图9 目标II非周期优化构型
周期设置Mx×My为5×5、8×8时结构宏观拓扑构型和子区域构型如表3所示。图10为热负荷作用5 000 s时,目标I、II在周期设置下目标函数随迭代步数变化曲线。

表3 不同热负荷作用时间下周期性结构宏观拓扑构型和子区域构型
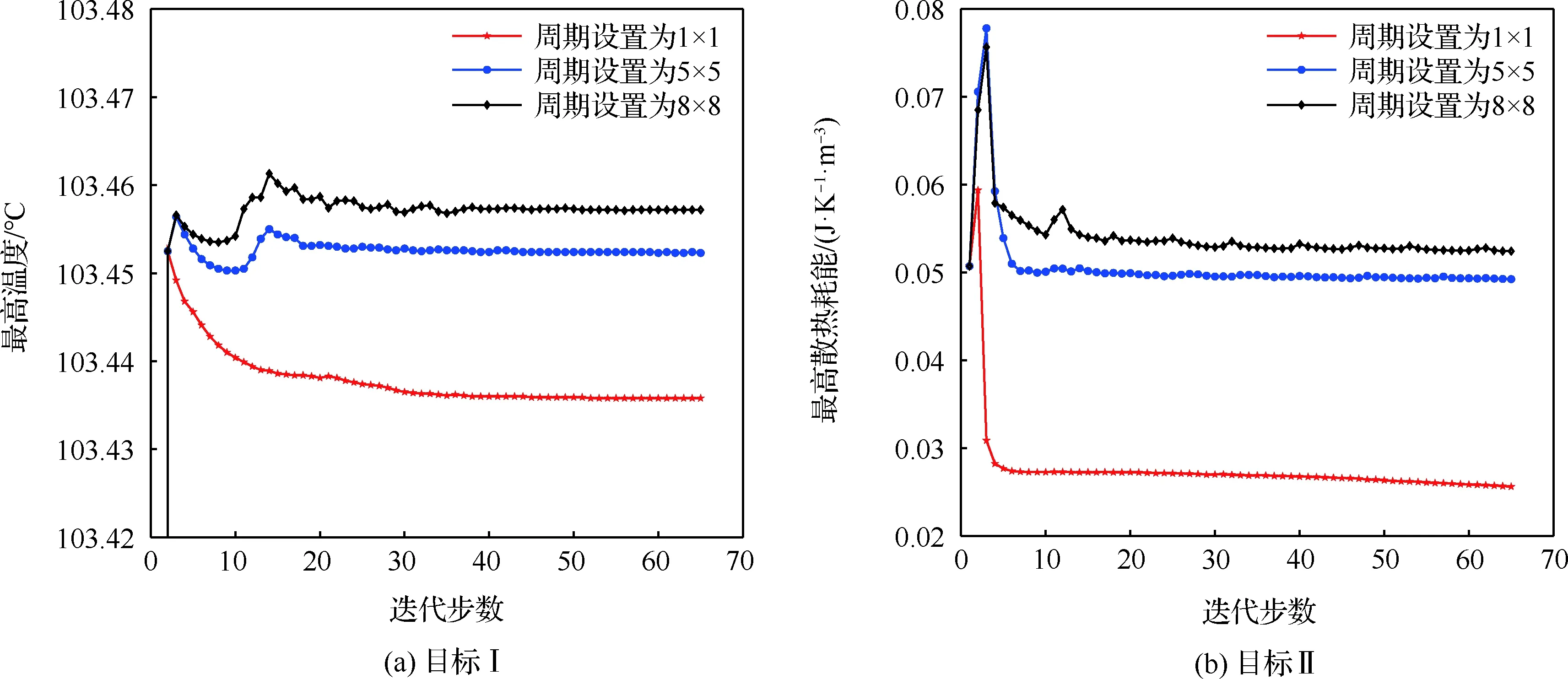
图10 目标函数值随迭代步数变化曲线
由表3可知,不同设计边界、多热源工况下仍可获得材料分布合理、边界清晰的周期性宏观拓扑构型及其子区域构型,进一步证明了该方法的有效性。周期性约束会对拓扑构型产生较大影响,结合图10可以发现,优化目标总体上随子区域数目增加而变差。同时从迭代曲线可以看出其收敛过程较为平稳,进一步证明该算法的稳定性。
3.3 三维算例
考虑三维数值算例,选取几何尺寸为60 mm×60 mm×12 mm的设计区域开展研究,并将其离散为60×60×12个八节点正方体单元。设计域如图11所示,在设计域中心点施加强度为P(t)=1 W的恒定热源,8个顶点处温度恒为0 ℃,其余边界绝热,总时间历程tf=1 000 s,过滤半径rmin=1.8。材料Mat-1、Mat-2和 Mat-3颜色分别设置为绿、红、蓝。
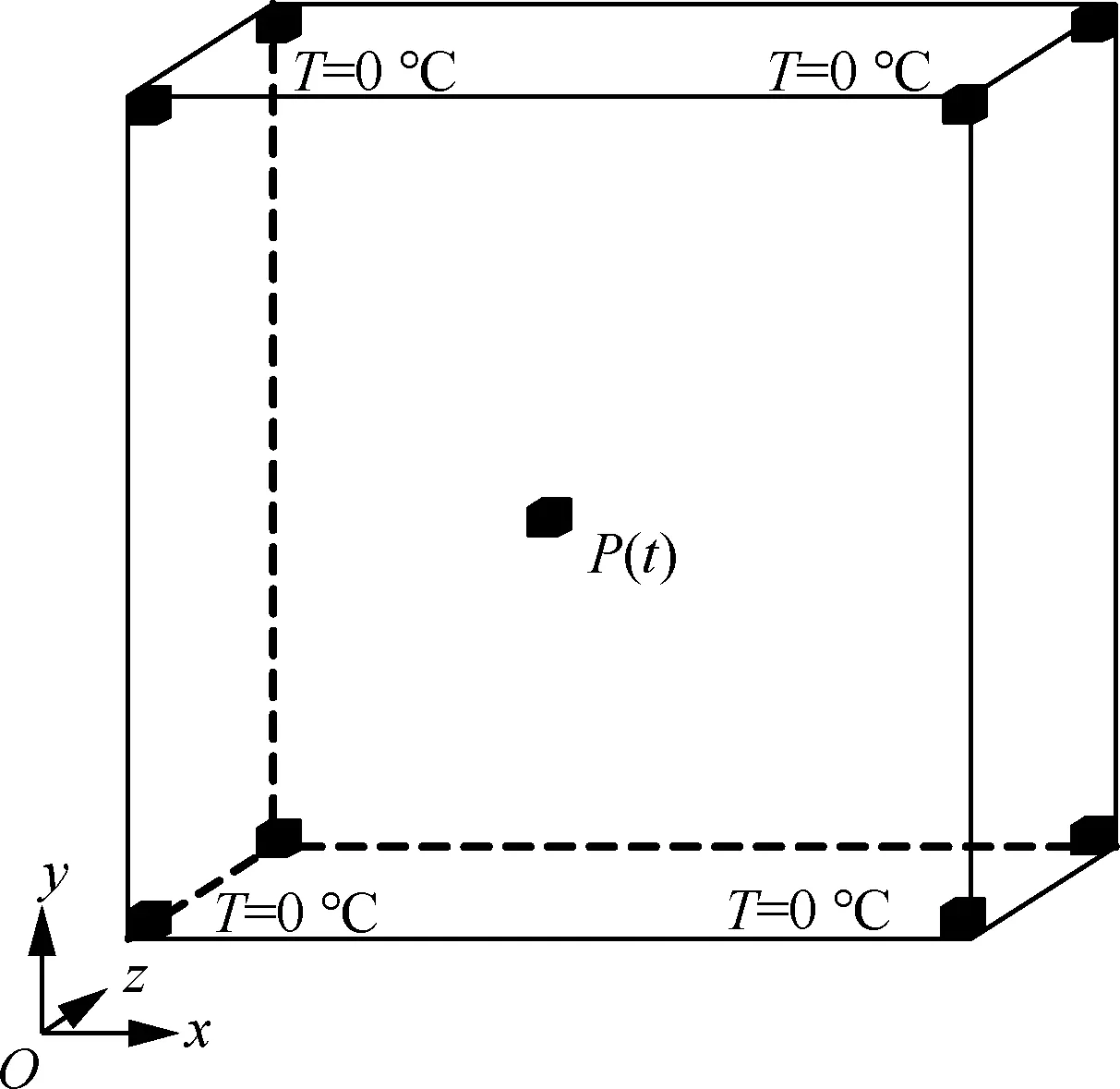
图11 3D结构设计域
针对三维结构围绕目标I和目标II进行设计优化研究。周期设置Mx×My×Mz分别设置为1×1×1、2×2×1、3×3×1,热负荷作用时间取800 s进行分析。拓扑优化构型、节点最高温度和最高散热耗能如表4所示。
由表4可知,所提方法可实现基于三维的周期性结构瞬态热传导拓扑优化设计,且拓扑构型能与二维对应,证明该设计的可行性。当周期设置为1×1×1时,目标I拓扑构型呈现从加热点到8个顶点扩散的立体×形,这在周期设置3×3×1子区域中效果明显,而目标II拓扑构型则呈现向顶点连接处扩散的花形,这同结构的设计目标和热负荷作用时间相关。对于周期结构,随着子区域数的增加,结构的散热性能变弱,两种设计目标函数值呈增加趋势,这体现尺寸效应对优化性能的影响,与二维算例相同。
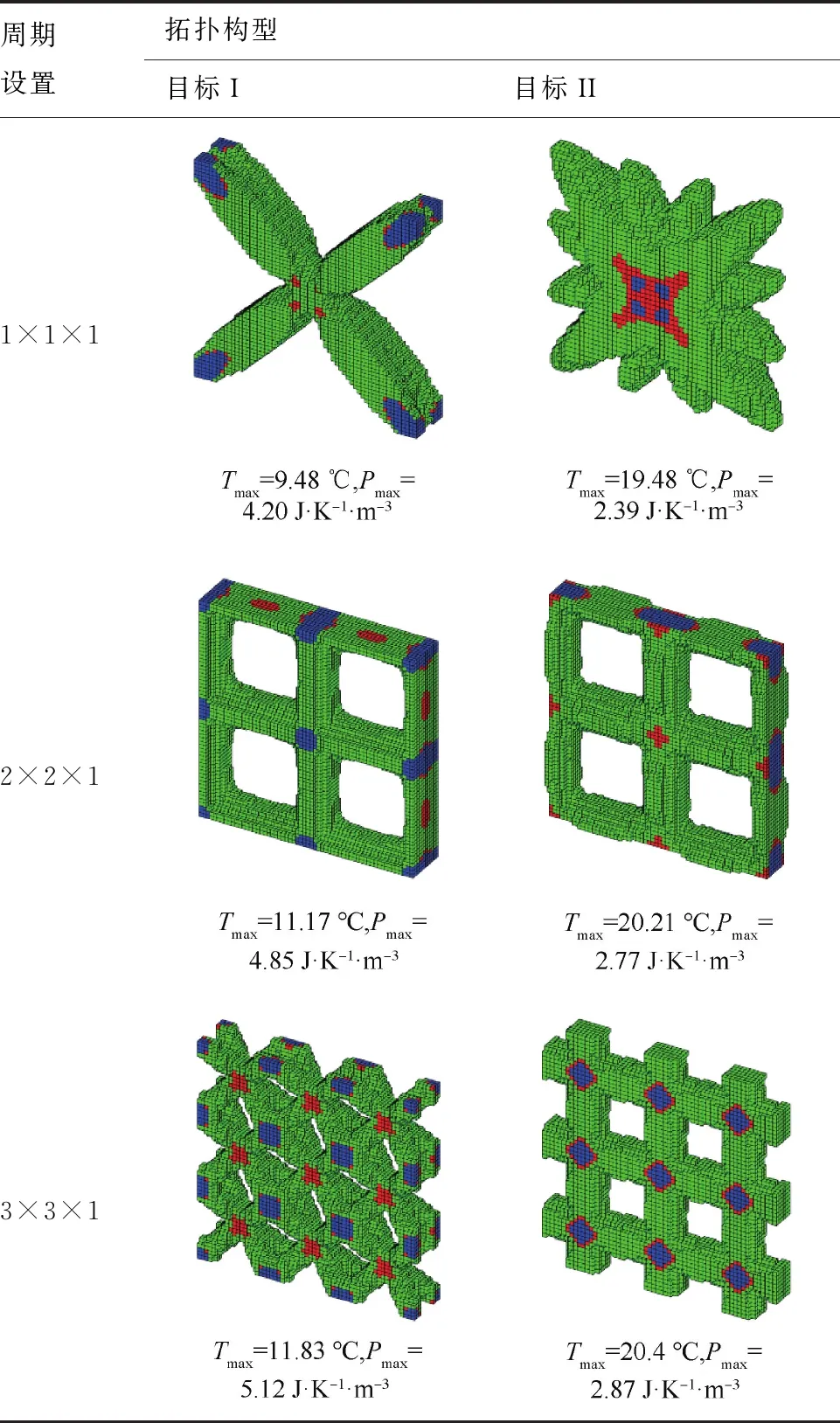
表4 不同目标下周期性拓扑构型、最高温度和散热耗能值
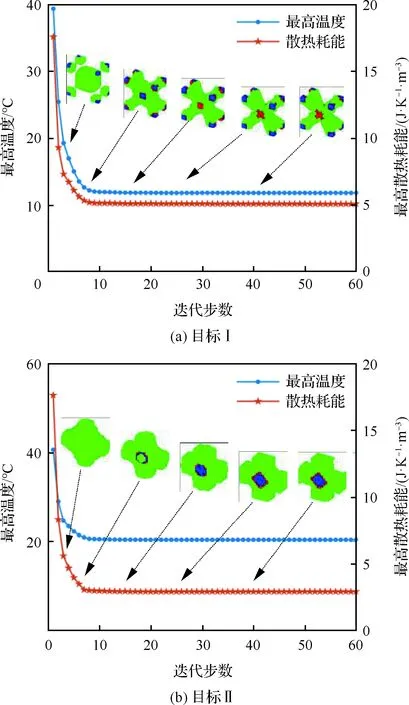
图12 最高温度和最高散热耗能随迭代步数变化曲线
周期设置3×3×1下目标I、II的子区域构型、最高温度值和最高散热耗能值随迭代步数变化曲线如图12所示。不难看出目标函数能快速达到平稳状态,且迭代过程中未出现波动现象。优化结果中材料Mat-1占比最大,材料Mat-2、Mat-3,即具有较高导热和热容系数材料,多集中在中间点和顶点位置,且材料分布呈向四周扩展的趋势,这主要受宏观结构体积约束的限制。结合表4可以发现目标I的最高温度迭代曲线低于目标II,目标II的最高散热耗能迭代曲线低于目标I,这是由不同设计目标造成的。
4 结 论
1) 建立了考虑瞬态效应的周期性多材料传热结构拓扑优化模型,对比分析了不同设计目标下的优化构型,通过二维与三维数值算例验证该方法的有效性。
2) 基于Ordered-RAMP插值模型的多材料结构拓扑优化参数设置简便,原理易于理解,可充分发挥各材料的性能优势。
3) 所获的周期性多材料传热结构,材料分配合理、布局清晰,周期性明显,具有较好的工程应用前景。
4) 优化结果表明,不同设计目标和热负荷作用时间下均可得到周期性拓扑构型,且宏观构型、子区域构型存在差异性;周期性约束会对拓扑构型产生影响,子区域数目越多优化目标越差。

