基于二阶拟合模型的SiC双向LLC数字同步整流控制

李浩然 崔超辉 王生东 张之梁 胡存刚

基于二阶拟合模型的SiC双向LLC数字同步整流控制

李浩然1崔超辉1王生东2张之梁3胡存刚1

（1. 安徽大学电气工程与自动化学院 合肥 230039 2. 中国电子科技集团公司第五十五研究所 南京 210016 3. 南京航空航天大学自动化学院 南京 211106）

传统LLC同步整流控制采用高频信号检测的方法，易受高d/d影响导致占空比丢失，导通损耗增大；而直接给定占空比的方法，无法跟随负载变化，宽负载范围下导通损耗急剧上升。该文提出基于二阶拟合模型的SiC双向LLC数字同步整流控制，跟踪负载和开关频率的变化，实时计算同步整流导通时间。LLC一次侧和二次侧开关管开通时刻一致，同步整流管关断时刻由所计算的同步整流导通时间决定。在宽负载范围内实现了低导通损耗，无需检测高频信号，抗干扰性强。该文分析当谐振电感和输出等效电阻存在10% 误差时，同步整流导通时间误差最大仅为2.73%。搭建6.6kW SiC双向LLC充电机实验样机，实验验证了所提同步整流控制的有效性。相比于传统LLC同步整流控制，所提控制正向满载6.6kW下效率提高了0.36%，反向满载3.3kW下效率提高了0.29%。

LLC变换器 同步整流 双向 SiC MOSFET 拟合模型

0 引言

LLC谐振变换器具有宽零电压软开关（Zero Voltage Switching, ZVS）和零电流软开关（Zero Current Switching, ZCS）的优势，且励磁电感可集成在变压器中实现高功率密度，是近年来备受关注的隔离型拓扑结构之一[1-2]。结合具备高频、高压优良特性的宽禁带器件，LLC变换器可进一步实现极高的效率和功率密度，广泛应用在电动汽车、储能系统及光伏系统中[3-4]。

同步整流（Synchronous Rectifier, SR）技术是采用MOSFET代替整流二极管，可显著降低整流导通损耗，是实现LLC变换器高效率的最有效方法之一。理想情况下，当电流流过SR管体二极管时，控制器立刻驱动SR MOSFET导通，使电流从体二极管转移到MOSFET沟道中。当SR管导通电流为零时，驱动信号立刻关断SR MOSFET，防止功率回流。

现有LLC变换器同步整流方法常分为两类：第一类是通过测量高频电压/电流信号的方法，控制同步整流管的开通或关断；第二类是非直接测量方法，直接给定同步整流占空比或通过建模计算导通占空比。

第一类方法中，通过测量一次侧谐振腔电流或SR管的漏源极电压或电流，控制SR管开通或关断。文献[5-6]中，利用电流互感器检测一次侧谐振电流，实现对SR管的控制。文献[7]中，采用电流互感器检测变压器二次电流，控制同步整流管开通或关断。然而，利用传感器测量电流的方案，需额外的电流传感元件，损耗较大，且电流互感器增加了变换器的体积。文献[8]中，基于LLC变换器一次侧谐振电流和输出电压控制同步整流管的导通时间，实现同步整流策略。但在过谐振或完全谐振的情况下，同步整流和一次侧驱动完全同步，导致不同负载下占空比存在丢失，使得同步整流管导通损耗增加，效率降低。

文献[9]中，通过测量SR管的漏源极电压来控制功率管开通和关断，检测漏源极电压同步整流策略如图1所示。当漏源极电压低于导通阈值时，说明此时体二极管有电流流过，检测芯片输出驱动信号使其导通。关断时，通过判断漏源极电压的大小，控制同步整流管关断。文献[10]也是通过测量漏源极电压来实现同步整流功能。它有精确的关断阈值和低导通时间，最高工作频率达1MHz。然而，该芯片测量的最大电压仅为200V，更高电压下便难以有效工作。文献[11-14]的原理是类似的，均通过测量漏源极电压来控制SR管。

图1 检测漏源极电压同步整流策略

上述方法在低电压下是有效的（几十V），但在高电压下并不适用（高达700V）。高d/d下，寄生电感极易影响检测电路的准确性。检测电路也增加了变换器的复杂性和成本，特别是在双向LLC应用中。

文献[15]中采用模拟同步整流芯片实现同步整流功能。同步整流芯片最大耐压为200V，但在漏源极上采用电阻分压的方案，漏源极电压经过分压后送入同步整流芯片检测口。通过调整分压电阻的比值，可实现同步整流芯片在高于200V电压的情况下工作。但是，该方案对分压电阻的精度要求较高，多个分压电阻值之间的误差，可能导致SR芯片输出驱动不同，影响电路正常工作。

第二类方法是非直接测量方法。文献[16]中，将同步整流管占空比与输出电压的乘积视为常数，计算输出电压变化时的同步整流占空比。但它不适合电动汽车动力电池充电的应用场景，因为当电池电压增加时，同步整流占空比会不断下降，这是不准确的。文献[17]利用LLC变换器的仿真模型，对同步整流管的开通和关断延迟时间进行仿真，并在两个查找表中预置开通和关断延迟时间，优化系统效率。但是，当LLC变换器谐振参数发生变化时，需要重新建立查找表，通用性较差。且该方法只考虑输出电流，忽略电池电压变化，不能反映实际输出功率，因此所输出的同步整流驱动信号精度有待进一步提高。

在文献[18-19]中，提出了两种相似的同步整流驱动方案，直接给定了同步整流管的导通时间。但该方法忽略了负载的变化，同步整流占空比存在丢失，使得同步整流MOSFETs的体二极管导通时间较长，导致导通损耗较大、效率不高。文献[20]中，同步整流导通时间只考虑了开关频率，忽略了负载变化，导致宽范围负载下，效率有待提高。

针对现有同步整流方案存在的检测电路复杂、抗干扰性弱以及同步整流导通占空比精度不高的问题，本文提出了基于二阶拟合模型的SiC双向LLC数字同步整流控制策略。通过在频域建立同步整流导通时间的解析模型，利用二阶多项式拟合原始复杂模型，简化计算同步整流导通时间，具备控制简单、抗干扰性强和SR导通时间精度高的优点。最后，基于所搭建的6.6kW SiC双向LLC充电机平台，验证所提同步整流控制的有效性。

1 基于二阶拟合模型的SiC双向LLC数字同步整流控制

为提高双向LLC变换器效率，提出了基于二阶拟合模型的SiC双向LLC数字同步整流控制。该控制通过准确计算同步整流管导通时间，从而显著降低同步整流管导通损耗，进一步提高效率。

1.1 基于二阶拟合模型的LLC同步整流正向控制

正向模式下，所提基于二阶拟合模型SR控制策略如图2所示。图2中，Dfor为SR导通时间；r为谐振频率；s和o分别为开关频率和等效输出电阻；00～02和00～02均为拟合常数；on_Q和on_s分别为一次侧和二次侧驱动的开通时刻；off_s为二次侧驱动的关断时刻；r和m分别为谐振电流和励磁电流；S1和S2分别为S1和S2的导通电流；ref和ref分别为电流参考和电压参考值；PI为比例积分控制器。Q1～Q4和S1～S4均为MOSFETs，采用了数模转换器（Analog-to-Digital Converter, ADC）进行采样，LLC变换器正向运行波形如图3所示。由图3可知，所提SR控制通过建立二阶拟合模型，考虑开关频率s和输出等效负载o的变化，实时计算同步整流管导通时间。一次侧开关管驱动信号和二次侧开关管驱动信号的开通时刻是相同的，但同步整流管关断时刻由计算出的SR导通时间决定。因此，同步整流导通时间可根据开关频率或输出负载的变化而变化。

图2 所提基于二阶模型的正向LLC同步整流控制

图3 正向LLC变换器波形

LLC变换器的输入电压为380～700V，输出电压调节为200～500V。在双向LLC变换器中，采用SiC MOSFET，充分利用其高电压和高开关频率的特性。LLC谐振频率在满载6.6kW时高达300kHz。

从图3可得，随着负载和开关频率的变化，所提同步整流控制可实时计算同步整流导通时间，降低同步整流管的导通损耗，优化效率。更高开关频率下，通过增加控制周期的时间，降低同步整流计算时间的占比，保证闭环运算和同步整流导通时间计算的完成。

英飞凌公司采用的传统单向同步整流方法，只考虑开关频率变化[20]，宽负载范围下的效率有待进一步提高。本文所提同步整流控制同时考虑开关频率和负载变化实时调整同步整流导通时间，效率更高。并且所提控制是基于数学模型，无需测量任何高频信号，不会受到高开关频率噪声的影响。

1.2 基于二阶拟合模型的LLC同步整流反向控制

反向模式下，所提基于二阶拟合模型的同步整流控制如图4所示，图5所示为LLC变换器反向运行波形。此时Q1～Q4为同步整流管。LLC反向运行时，励磁电感始终并联在输入电压两端，不参与谐振，反向LLC变换器电压增益特性与LC变换器一致。因此，反向LLC变换器始终固定工作在谐振频率点r，实现高效率。

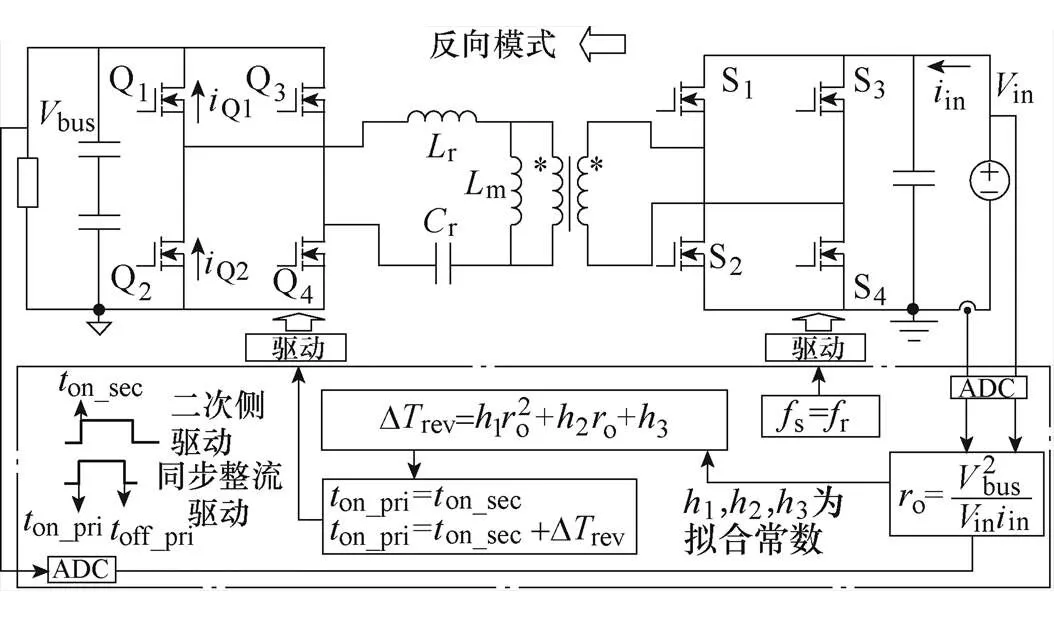
图4 所提基于二阶拟合模型的反向LLC同步整流控制

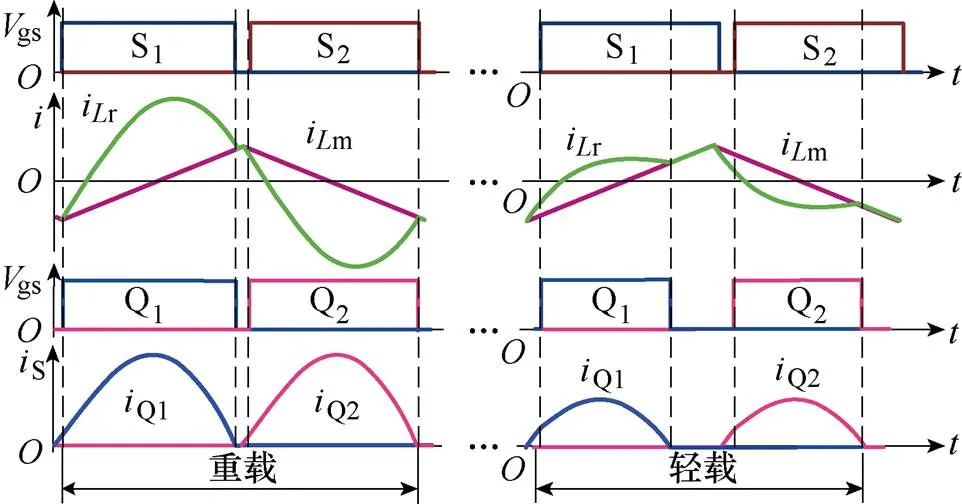
图5 反向LLC变换器工作波形

通过建立二阶拟合数学模型，考虑输出等效负载的变化，实现同步整流导通时间的在线计算。原二次侧开关管的开通时刻相同，但同步整流管关断时刻由所建数学模型计算出的同步整流导通时间决定。

所提双向同步整流控制的优点如下。

（1）通过建立数学模型，可以准确计算出同步整流导通时间，显著降低同步整流管体二极管的导通时间，减少导通损耗，进一步提高LLC效率。

（2）无需测量高频信号，对开关噪声的抗干扰能力强，并具有高效率和控制器计算资源少的优势。

2 数字同步整流控制正向LLC二阶拟合模型分析

2.1 正向同步整流导通时间频域模型

图6所示为LLC变换器正向运行的等效电路和工作波形。图中，ab为桥臂中点电压，in为LLC输入电压，j为同步整流管输出等效结电容，为同步整流管导通时间。为便于对模型进行分析，假设谐振电感、谐振电容和变压器是理想的，只考虑了基波，并将同步整流管输出等效结电容视为常数。

图6 正向LLC变换器的等效电路和工作波形

图6a中，RC为输出等效负载和同步整流管结电容的并联阻抗，其表达式为

其中

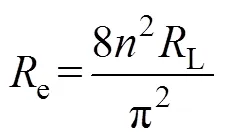
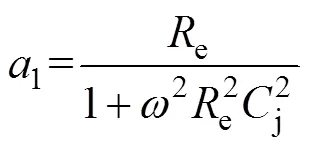
式中，L为输出阻抗；为变压器电压比。RC相位1表示为

RLC表达式为

其中

LRC的相位2表示为

输出阻抗o为

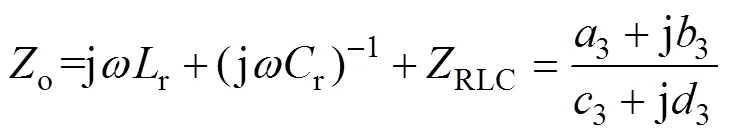
其中

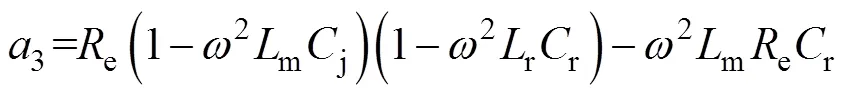
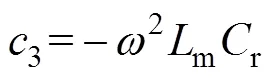
o的相位3表示为

假设

同步整流导通时间在时域可计算为

2.2 所提基于二阶拟合模型的SR算法

由于同步整流导通时间只与开关频率和输出负载有关，因此可简化算法。在保证LLC变换器高效率的同时，大幅减少数字信号处理器（Digital Signal Processor, DSP）的同步整流计算时间。

利用Matlab，选取二阶多项式作为拟合函数。开关频率小于谐振点时，SR导通时间拟合函数为

式中，00=3.955×10-6；10=-1.161×10-11；01=-3.44× 10-9；20=1.284×10-17；11=-2.266×10-15，02=6.749× 10-12。

开关频率大于谐振点时，SR导通拟合函数为

式中，00=3.56×10-6；10=-8.593×10-12；01=-5.847× 10-9；20=7.817×10-18；11=3.63×10-16；02=1.263× 10-11。在DSP程序中，采用上升-下降计数时，开关频率可计算为

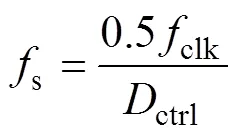
式中，clk为控制器工作频率；ctrl则来自闭环控制器的输出。本文采用的DSP型号为TI的TMS320F280049C，主频为100MHz。

SR运行周期的对比分析见表1。该表包含了等效输出负载的计算周期。它假设代码和堆栈在零等待状态内存中。从表1可看出，使用所提二阶拟合算法，DSP的SR计算周期大幅减少。

表1 SR所需DSP运行周期对比分析

Tab.1 Consumed running cycles in DSP for SR

图7所示为正向LLC导通时间对比。不同开关频率下，所提SR算法具有很高的拟合精度，满载下误差仅为2.28%和0.94%。因此，所提SR简化算法可实现高效率，同时所需DSP的计算资源更少。

2.3 电路参数漂移分析

2.3.1 输出等效电阻参数漂移分析

输出等效电阻由测量的输出直流电压和输出电流计算得到。分析温度对输出等效电阻影响，即分析温度变化对输出直流电压和电流影响的分析。

输出直流电压测量采用电阻分压的方式，如图8所示。图中，1、2和3为分压电阻，其值分别为5.1MW、3.9MW和47kW，1和2的温漂系数均为±100×10-6/℃，3温漂系数为±10×10-6/℃。输出电压o变化范围为200～500V，s为3的电压，经采样处理电路处理后送入DSP。

图8 电阻分压测量输出电压

采样电压s与o关系为

当温度为125℃、温升为100℃时，根据电阻温漂系数可得，1、2和3的电阻变化率分别为0.01%、0.01%和0.001%。此时采样电压s为

采样电压s进入DSP后进行离散化，采用12位采样，DSP采样标准参考电压为3.3V，输入至DSP内的离散电压采样值s_d为

s_d始终为整数值。本文闭环程序中，25℃下，经过采样拟合，DSP采样拟合电压o_dsp为

1和1分别是0.153和0.889 6，为采样电阻在25℃下的拟合值。当温度为125℃时，有

1为DSP采样拟合电压o_dsp与实际电压o的比值。当o分别为200V和500V时，1为0.990 93和0.988 26。当温升为100℃时，输出电压的测量最大误差为1.174%。

输出电流测量采用霍尔电流芯片ACS725LLCTR- 30AB-T，来自Allegro公司。图9所示为该芯片测量总误差随温度变化的曲线，Sigma表示标准差。由图9可知，当温度为125℃时，电流测量误差最大和最小分别为0.5%和-0.7%，即实际电流为o时，输出至DSP中的电流为1.005o或0.993o。

图9 电流芯片随温度变化的曲线

温度从25℃升到125℃，温升为100℃时，有

式中，e_nor为25℃下的输出等效电阻；e_max为125℃下的输出等效电阻；o和o分别为25℃下的输出直流电压和电流。因此，输出等效电阻在温升100℃下的最大测量误差为1.67%。

图10所示为输出负载存在误差时的分析。开关频率分别为300kHz和270kHz时，当等效输出负载存在10%的误差时，满载情况下，SR导通时间误差仅为0.58%和1.13%。因此，输出负载存在误差时，不会影响导通时间的计算准确度。

2.3.2 谐振电感参数漂移分析

图11所示为谐振电感存在误差时的分析。谐振电感存在气隙，气隙磁阻远大于磁心磁阻。

因此，当温度变化较大时，谐振电感值变化很小。根据图11，当谐振电感存在10%的误差，导通时间误差仅为2.73%和2.12%，不会影响所提算法的实现。

图11 LLC谐振电感存在误差（Vo=380V）

2.4 LLC变换器损耗分析

图12所示为正向LLC损耗分析。300kHz时，相比于传统算法，所提SR算法SR管损耗减少了27.7W。270kHz时，所提算法依旧可减少损耗，提高效率。因此，所提SR算法通过减小SR体二极管的导通时间，降低整流管导通损耗，提高效率。

图12 正向LLC损耗分析（Po=6.6kW）

3 数字同步整流控制反向LLC二阶拟合模型分析

3.1 反向同步整流导通时间二阶拟合模型分析

图13所示为反向模式下LLC的等效电路和波形。jeq为同步整流管的等效输出结电容。

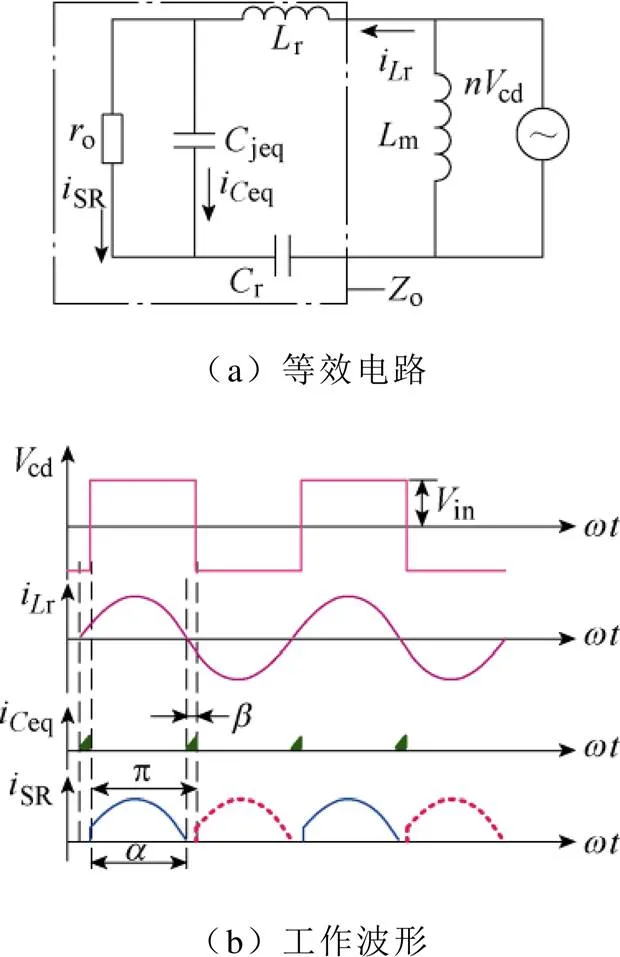
图13 反向LLC变换器等效电路和波形

由图13可知，等效输出阻抗o为

等效输出阻抗的虚部eq为

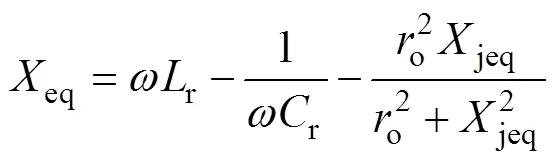
等效输出阻抗的实部eq为

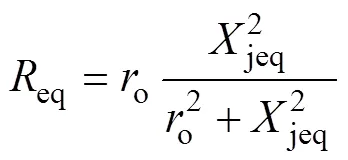
基于式（29）、式（30），时间间隔表示为

SR导通时间为

反向模式下，LLC变换器始终在谐振点工作。由于SR导通时间只与负载有关，可以简化所提算法，减少DSP的计算耗时。利用Matlab，选取多项式作为拟合函数，SR导通时间拟合函数为

式中，1=1.635×10-12；2=-1.998×10-9；3=1.649× 10-6。

表2所示为SR运行周期的比较。采用所提的二阶拟合模型算法，所需的运行周期大幅减少。

图14所示为所提基于二阶拟合模型的SR算法和原始SR算法的导通时间对比。满载工况下，所提二阶拟合模型和原始模型的误差只有0.39%。因此，所提基于二阶拟合模型的算法具有很高的拟合精度。

表2 SR所需DSP运行周期对比分析

Tab.2 Consumed running cycles in DSP for SR

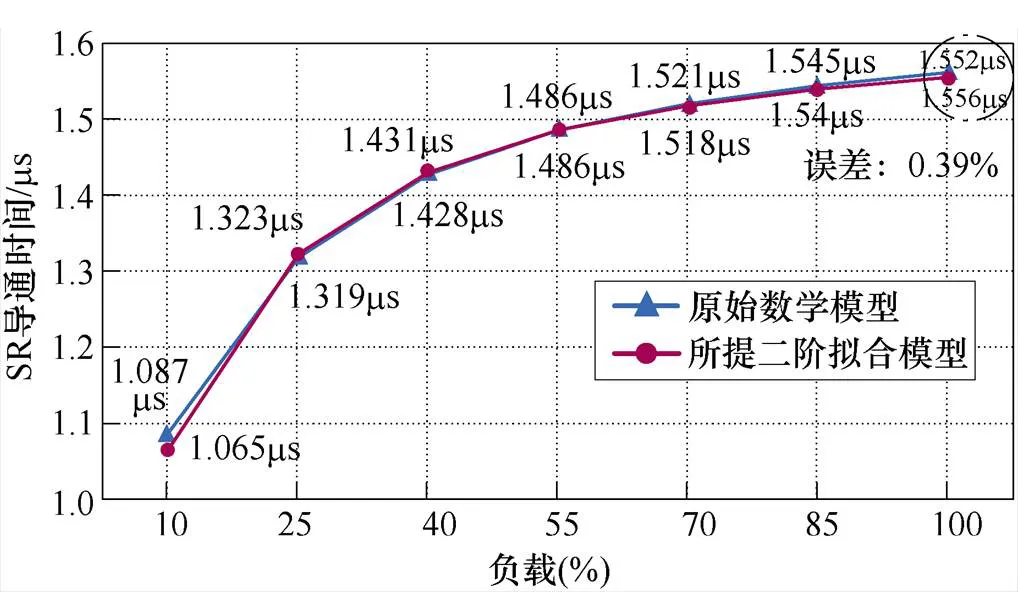
图14 SR导通时间比较（fs=300kHz, Vbus=400V）

3.2 参数漂移影响和损耗分析

图15所示为输出等效电阻存在误差时，实际SR导通时间对比分析。满载时，当输出电阻负载存在10%误差时，SR导通时间误差仅为0.72%。因此，输出负载存在误差时，不影响所提SR算法的实现。

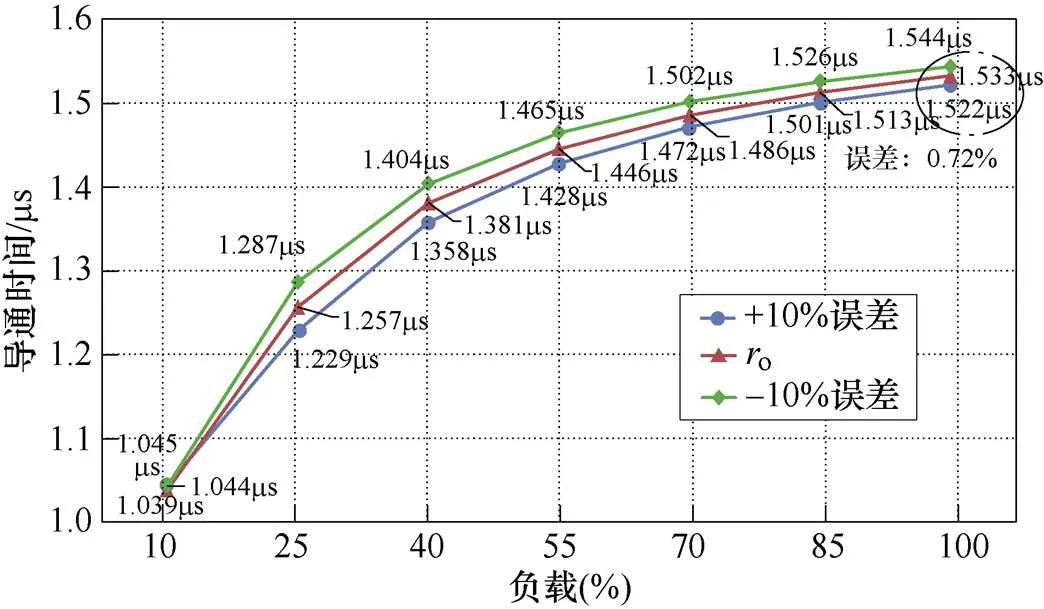
图15 输出等效电阻存在误差（Vbus=450V, fs=300kHz）

图16所示为LLC变换器反向运行的损耗分析。相比传统SR控制，基于所提SR控制，反向LLC变换器同步整流的导通损耗减少了11.2W，明显提升了反向LLC的效率。

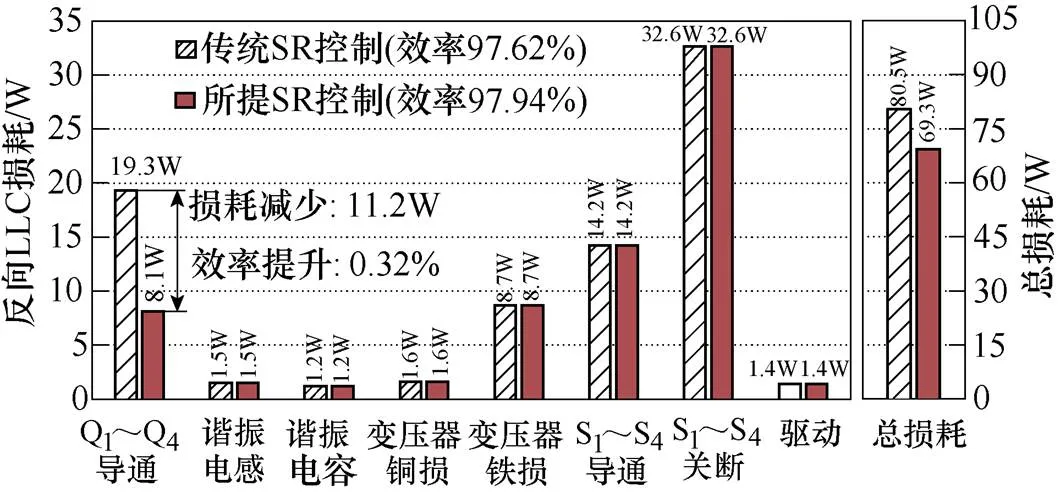
图16 反向LLC损耗分析（Vbus=520V, fs=300kHz）

4 实验验证

4.1 实验样机

为了验证所提SR控制的有效性，搭建了一台6.6kW双向充电机，拓扑结构如图17所示，实验样机如图18所示。前级为交错并联图腾柱功率因数校正（Power Factor Correction, PFC）电路，后级为LLC变换器。采用Wolfspeed公司的SiC MOSFETs（C3M0065090D），电路详细参数见表3。

图17 双向LLC充电机拓扑结构

图18 6.6kW双向LLC充电机实验样机

表3 双向LLC充电机电路参数

Tab.3 Parameters of bidirectional LLC charger

（续）

4.2 所提LLC同步整流控制正向运行实验

图19所示为LLC变换器正向运行下采用所提SR控制的运行波形。由图中可看出，开关频率为270kHz，负载分别为2.6kW和6.6kW时，所提控制可精确地控制SR驱动导通时间，降低体二极管导通时间，减少体二极管的导通损耗。当开关频率为305kHz时，依旧可实现很好的控制效果。

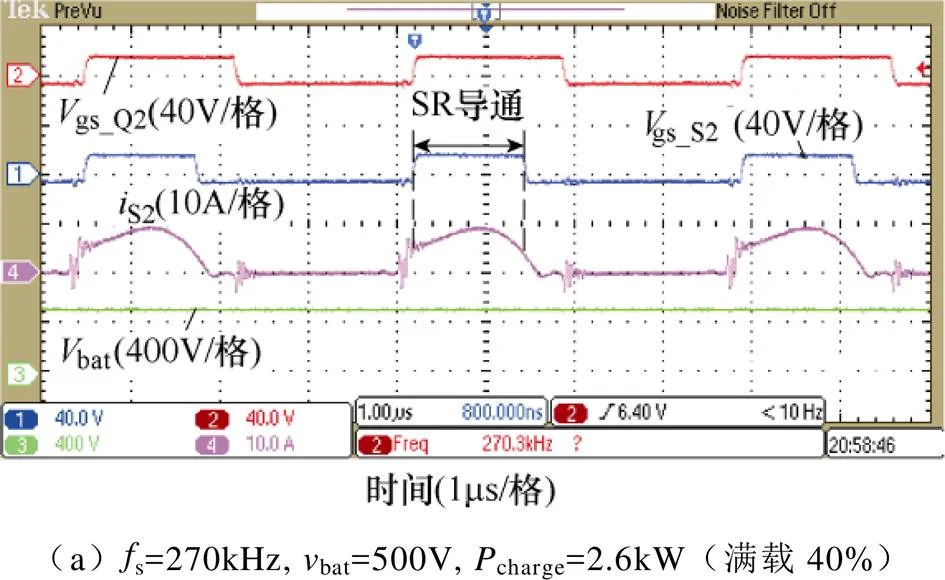
图20所示为LLC变换器在负载突变下的波形。图20b是图20a中区域1的放大图。可以看出，当负载从4.4kW突变到1kW时，可实现所提SR控制。图21为同步整流算法运行时间对比。相比原始复杂模型，采用所提基于二阶拟合模型的同步整流算法，DSP运行时间降低了超过60%。

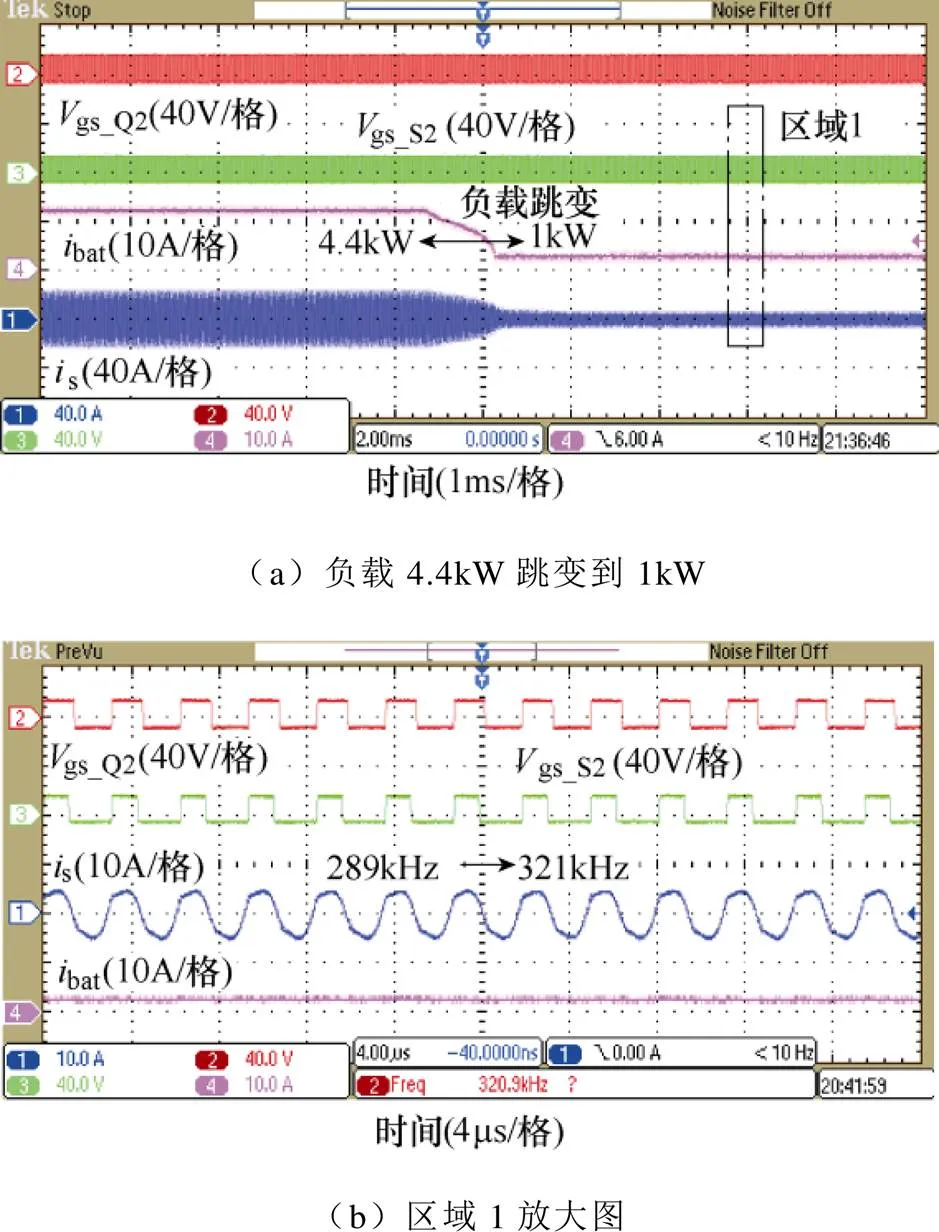
图20 所提同步整流控制下的负载跳变（Vbat=320V）

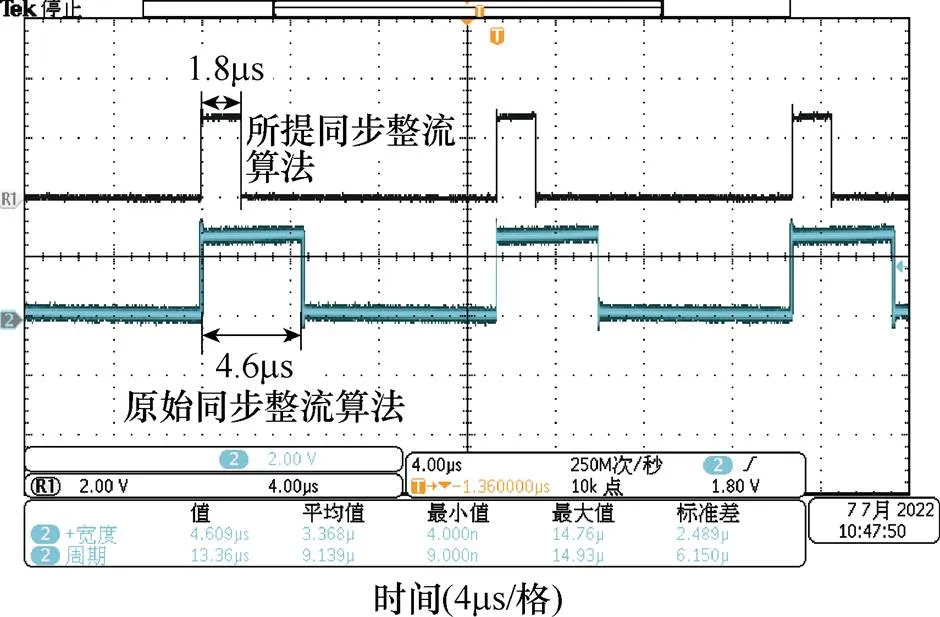
图21 正向同步整流运行时间对比

图22给出所提控制和传统SR控制的效率对比。传统控制是基于文献[20]，只考虑了开关频率的变化，忽视了负载的变化。SR管开通时刻由一次侧开关管开通时刻延迟一定时间得到。开关频率小于或等于谐振频率时，SR管导通时间等于半个谐振周期减去驱动延迟时间和死区时间。开关频率大于谐振点时，SR管关断时刻超前于一次侧开关管关断时刻，超前时间等于驱动回路延迟时间。

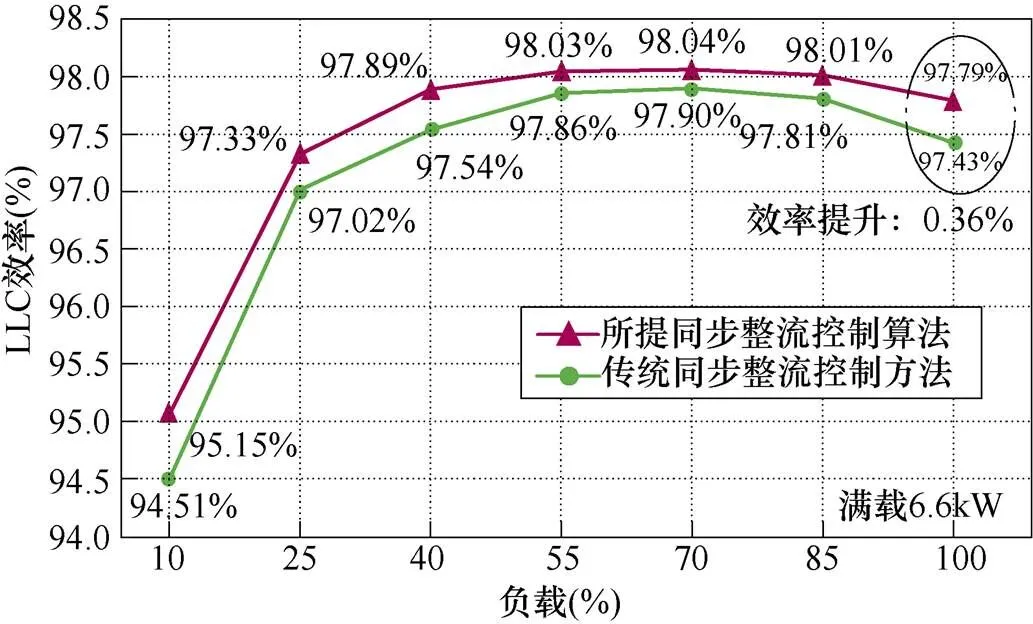
图22 正向LLC变换器效率对比（vbat=420V, fs=300kHz）

由图22可知，所提SR控制可根据负载变化实时调节SR导通时间，降低SR管导通损耗，提高效率。满载6.6kW下，所提控制效率提升高达0.36%。

4.3 所提LLC同步整流控制反向运行实验

图23给出了反向LLC变换器实验波形。为实现高效率，LLC变换器反向运行时，始终工作在300kHz。当负载功率分别为1.6kW和3.3kW时，所提SR控制很好地调节了SR导通时间，跟随负载变化。因此，可极大地降低SR管导通损耗，提高效率。

反向LLC变换器负载突变如图24所示。图24b为图24a中区域2的放大图。当负载从0.2kW突变到3.3kW时，所提控制可实现良好的负载跟踪。

图24 反向LLC负载跳变（Vbus=430V, fs=300kHz）

图25所示为LLC变换器反向运行时两种算法实际运行时间。相比原始复杂模型算法，所提算法在DSP中的运行时间减少了约75%。

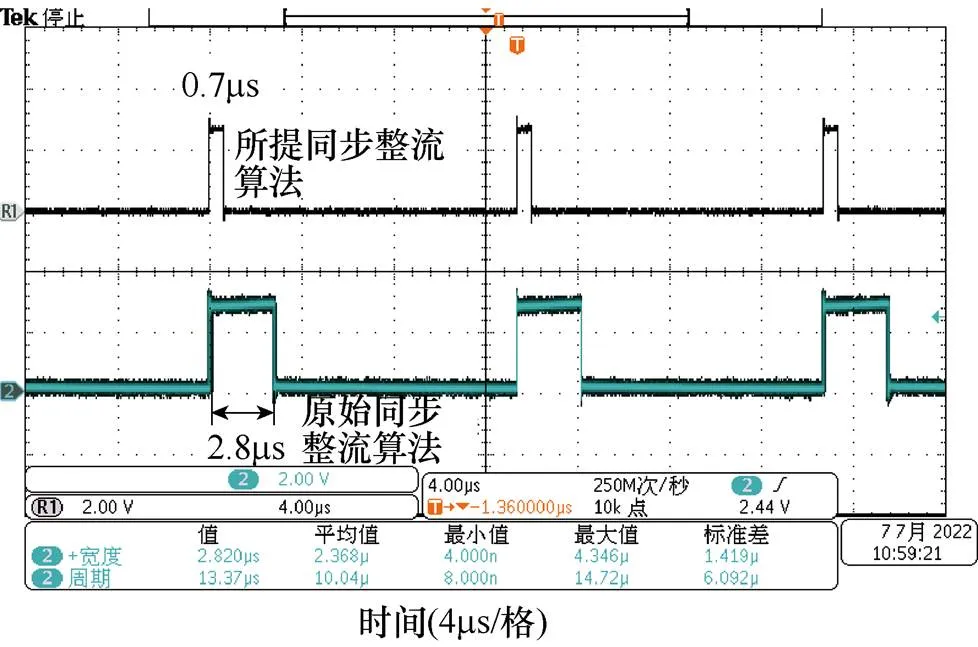
图25 反向LLC变换器同步整流算法运行时间

图26所示为LLC反向运行时，所提SR控制和传统SR控制的效率对比。相比传统控制[20]，满载3.3kW条件下，所提SR控制效率提升达到0.29%，具备良好的控制效果，且不增加任何元器件和成本。

图26 反向LLC变换器效率对比Vbus=520V, fs=300kHz

5 结论

本文提出了基于二阶拟合模型的SiC双向LLC数字同步整流控制策略。通过在频域建立LLC同步整流导通时间的解析模型，利用二阶多项式拟合原始的复杂模型，简化同步整流导通时间在控制器中的计算。一次侧开关管和二次侧同步整流管驱动开通时刻一致，而同步整流管关断时刻则由所计算的导通时间决定。所提控制具有实现简单、抗干扰性强和SR导通时间计算精度高的优点。分析了当谐振电感和输出等效电阻存在10%误差时，同步整流导通时间的误差最大仅为2.73%，因此所提控制具备较强的鲁棒性。

最后，本文搭建了一台6.6kW 300kHz SiC双向LLC充电机实验样机，验证了所提控制的有效 性。正向模式下，相比传统控制，所提SR控制在满载6.6kW下效率提高了0.36%；反向模式下，相比传统控制，所提SR控制3.3kW下效率提高了0.29%。

[1] 汤欣喜, 邢岩, 吴红飞, 等. 兼顾稳态效率和暂态升压能力的LLC变换器[J]. 电工技术学报, 2020, 35(4): 767-774.

Tang Xinxi, Xing Yan, Wu Hongfei, et al. An improved LLC converter considering steady-state efficiency and transient Boost capability[J]. Transa- ctions of China Electrotechnical Society, 2020, 35(4): 767-774.

[2] 石林, 刘邦银, 段善旭. 一种基于Burst-PWM混合控制的LLC谐振变换器宽电压范围输出策略[J]. 电工技术学报, 2019, 34(22): 4772-4780.

Shi Lin, Liu Bangyin, Duan Shanxu. A Burst-PWM hybrid control method for wide output voltage range of LLC converter[J]. Transactions of China Electro- technical Society, 2019, 34(22): 4772-4780.

[3] 王生东, 李浩然, 顾占彪, 等. 便携式充电CRM图腾柱功率因数校正过零检测延迟与交错相位误差补偿控制[J]. 电工技术学报, 2022, 37(1): 12-23.

Wang Shengdong, Li Haoran, Gu Zhanbiao, et al. Compensation control of zero current detection delay and interleave phase error for CRM totem-pole power factor correctionin portable charging[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 12-23.

[4] 丁超, 李勇, 姜利, 等. 电动汽车直流充电系统LLC谐振变换器软开关电压边界分析[J]. 电工技术学报, 2022, 37(1): 3-11.

Ding Chao, Li Yong, Jiang Li, et al. Analysis of soft switching voltage boundary of LLC resonant con- verter EV DC charging system[J]. Transactions of China Electrotechnical Society, 2022, 37(1): 3-11.

[5] Wu Xinke, Hua Guichao, Zhang Junming, et al. A new current-driven synchronous rectifier for series- parallel resonant (LLC) DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 289-297.

[6] Huang Daocheng, Fu Dianbo, Lee Fred C. High switching frequency, high efficiency CLL resonant converter with synchronous rectifier[C]//2009 IEEE Energy Conversion Congress and Exposition, San Jose, 2009: 804-809.

[7] Zhang Junming, Liao Jiawen, Wang Jianfeng, et al. A current-driving synchronous rectifier for an LLC resonant converter with voltage-doubler rectifier structure[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1894-1904.

[8] 洪良, 杜建华, 王均, 等. 非对称半桥LLC谐振变换器同步整流数字设计[J]. 电源学报, 2018, 16(4): 113-119.

Hong Liang, Du Jianhua, Wang Jun, et al. Digital design for synchronous rectification used in LLC resonant converter with asymmetrical half-bridges[J]. Journal of Power Supply, 2018, 16(4): 113-119.

[9] Cheng Lifeng, Liu Teng, Gan Hongjiang, et al. Adaptive synchronous rectification control circuit and method thereof: United States, US 7.495.934[P]. 2009-02-24.

[10] On semiconductor. Secondary side synchronous recti- fication driver for high efficiency SMPS topo- logies[EB/OL].[2022-05-31]. http://www.onsemi.cn/ pub/Collateral/NCP4305-D.PDF

[11] Amiri Peyman, Botting Chris, Craciun Marian, et al. Analytic-adaptive LLC resonant converter syn- chronous rectifier control[J]. IEEE Transactions on Power Electronics, 2021, 36(5): 5941-5953.

[12] Feng Weiyi, Lee Fred C, Mattavelli Paolo, et al. A universal adaptive driving scheme for synchronous rectification in LLC resonant converters[J]. IEEE Transactions on Power Electronics, 2012, 27(8): 3775-3781.

[13] Fei Chao, Li Qiang, Lee Fred C. Digital imple- mentation of adaptive synchronous rectifier (SR) driving scheme for high-frequency LLC converters with microcontroller[J]. IEEE Transactions on Power Electronics, 2018, 33(6): 5351-5361.

[14] Wang Dong, Liu Yanfei. A zero-crossing noise filter for driving synchronous rectifiers of LLC resonant converter[J]. IEEE Transactions on Power Electronics, 2013, 29(4): 1953-1965.

[15] Li Haoran, Bai Lei, Zhang Zhiliang, et al. A 6.6kW SiC bidirectional on-board charger[C]//2018 IEEE Applied Power Electronics Conference and Expo- sition, San Antonio, 2018: 1171-1178.

[16] Abe Seiya, Yang Sihun, Shoyama Masahito, et al. Adaptive driving of synchronous rectifier for LLC converter without signal sensing[C]//2013 IEEE Applied Power Electronics Conference and Expo- sition, Long Beach, 2013: 2048-2051.

[17] Duan Chen, Bai Hua, Guo Wei, et al. Design of a 2.5kW 400/12V high-efficiency DC/DC converter using a novel synchronous rectification control for electric vehicles[J]. IEEE Transactions on Trans- portation Electrification, 2015, 1(1): 106-114.

[18] Wang Jing, Lu Bing. Open loop synchronous rectifier driver for LLC resonant converter[C]//2013 IEEE Applied Power Electronics Conference and Expo- sition, Long Beach, 2013: 2048-2051.

[19] Yeon Cheol-O, Kim Dong Kwan, Lee Jae-Bum, et al. Digital implementation of optimal SR ON-time control and asymmetric duty control in LLC resonant converter[C]//2015IEEE Energy Conversion Congress and Exposition Asia, Charlotte, 2015: 2031-2037.

[20] Infineon Corporation. 3300W 52V LLC with 600V coolMOSTM CFD7 and XMCTM[EB/OL].[2022-05-31]. https://www.infineon.com/dgdl/InfineonEvaluationboard_ EVAL_3K3W_LLC_HB_CFD7-ApplicationNotes-v0 1_00-EN.pdf?fileId=5546d4626cb27db2016d3a60583725dc.

Two-Order Fitting Model-Based Digital Synchronous Rectifier Control for SiC Bidirectional LLC Converter

11231

（1. School of Electrical Engineering and Automation Anhui University Hefei 230039 China 2. The 55th Research Institute of CETC Nanjing 210016 China 3. College of Automation Engineering Nanjing University of Aeronautics and Astronautics Nanjing 211106 China）

Conventional LLC synchronous rectifier (SR) typically senses high-frequency signals, easily affected by high d/dresulting in duty cycle loss and high conduction loss. The SR method with a given duty cycle cannot track load variations and causes high conduction loss in a wide load range. A two-order fitting model-based digital synchronous rectifier control is proposed for the bidirectional SiC LLC converter, which tracks load variations and switching frequency to calculate the SR on-time online. The turn-on instants between the primary and secondary switching devices are identical, while the calculated SR on-time determines the SR turn-off instants. The proposed control achieves low conduction loss and has high immunity to high switching noise without sensing high-frequency signals. When the resonant inductor and output load have 10% tolerances, the maximum tolerance for the SR on-time is only 2.73%. A prototype of a 6.6kW SiC bidirectional LLC charger was built. Compared with the conventional LLC SR control, the efficiency improvement is up to 0.36% at 6.6kW in the forward mode, and 0.29% at 3.3kW in the reverse mode.

LLC converter, synchronous rectifier, bidirectional, SiC MOSFET, fitting model

10.19595/j.cnki.1000-6753.tces.220973

TM461

安徽省自然科学基金杰青项目（2108085J24）、安徽省自然科学基金青年项目（2108085QE239）和安徽省高校自然科学研究项目（KJ2021A0007）资助。

2022-05-31

2022-07-06

李浩然 男，1991年生，博士，讲师，研究方向为双向DC/DC变换技术、高频功率变换技术。E-mail: haoranli@ahu.edu.cn

胡存刚 男，1978年生，教授，博士生导师，研究方向为多电平变换器、光伏发电和微电网。E-mail: hcg@ahu.edu.cn（通信作者）

（编辑 陈 诚）