从一堂课看数学课堂教学有效性

◎周先莉

(南京市溧水区石湫中学，江苏 南京 211222)

引 言

新课程改革以来，广大数学教师对数学课堂教学进行了不断的探索和研究，得出了许多值得学习的符合新课标理念的教学模式，但不管是何种教学模式，教学是否具有有效性都是检测其是否成功的重要指标.有效的课堂教学是教师在达成教学目标和促进学生发展两方面都取得成功的前提条件.不论课程改革如何发展，推动课堂教学有效性的不断提高都是我们广大教师的职责所在，也是我们教师永恒的追求.当前，围绕打造“高效课堂”的教科研活动在全国各地积极开展，大家都在寻求有效课堂的策略.本人前不久也参加了全区关于“如何提高课堂教学有效性的研讨”教研活动.听取了一节公开课：“菱形的判定”，对其中的一些教学环节进行了一些思考，对课堂教学有效性有了一些新的体会.下面就结合本节课谈谈自己几点浅显的认识.

1 利用课堂教学过程中的预设和生成的动态调整提高课堂教学有效性

1.1 教学片段

教师：上节课我们学习了菱形的性质，下面请一位同学说说菱形有哪些性质.

学生1：对边平行、四边相等，对角相等，对角线互相垂直平分.

学生2：菱形既是轴对称图形又是中心对称图形.

教师：很好，今天我们来学习菱形的判定.你知道菱形的定义吗？目前你会判定一个四边形是否是菱形吗？

学生3：有一组邻边相等的平行四边形叫菱形.

教师：很好，根据定义我们知道：四边形满足两个条件：一组邻边相等、是平行四边形，就可以判定它是菱形.(教师板书并将两个条件做出标记)

教师：同学们想一想，平行四边形再加上一个什么条件是菱形呢？

学生4：对角线互相垂直平分的平行四边形是菱形.

教师：(有点着急)什么？你再说一遍，还要说平分吗？

学生4：不要了.(说得有点勉强)

教师：同学们说这里为什么不需要说平分了？

学生(部分)：因为已经说是平行四边形了.

教师：对了.下面我们就来探究对角线互相垂直的平行四边形是不是菱形.

……

1.2 教学反思

从以上的教学片段可以看出，教师做了精心设计，教学流程很顺畅，语言也比较规范.但在学生4 回答完问题后，教师急了，因为这出乎教师意料，学生出现了问题，怎么办呢？这时教师急忙对学生4的回答进行了干预，把学生“引导”到了正确的答案上来，并借助其他同学把这个问题给顺利地处理了.我感到有点意外和惋惜，多好的一个课堂生成的问题，教师怎么就这么轻描淡写地过去了呢？后来我看了教案才知道，教师对学生可能出现的这种问题是有预设的.他的教案中设计了这样的教学环节：

思考交流：两条对角线互相垂直的四边形一定是菱形吗？为什么？看来他是想到后面专门来研究这个问题(尽管这个问题的价值已经大打折扣).诚然，这个问题是有价值的，它体现了几何问题中语言的严谨性和条件的不重复性，对学生今后的学习有很好的指导意义.但这样的处理真的合理吗？当预设的问题“意外”生成，教师该怎么办呢？

课堂教学方案具有“预设”与“生成”的特征，这就意味着课堂教学的设计方案与教学实施过程会存在一定的偏差，一堂优质的课绝对不会是仅仅在教师的“精准预设”下而“一帆风顺”地完成的.当“预设”遇到意外“生成”时，很可能会发生学生思维的碰撞，会带来一些新的教学资源.此时，教师应该怎么做？笔者以为，教师首先要快速判断“生成”的内容有无教学价值，从而适时地调整教学方案.然后，再由学生思考交流，对出现的“意外”进行再认识，这样不仅能在课堂上给学生展示的空间，调动学生的学习热情，更能让学生对知识有更全面的理解.这样的教学活动无疑是最有效的，也是最有价值的，这样的教学活动对提高课堂教学的有效性一定是有帮助的.

上面出现的问题，教师完全可以顺其自然，抓住出现的问题，交给每一位学生进行思考交流，发表各自的见解，引导学生真正弄清楚为什么是这样的.我想，这样的效果要比直接否定或由几个学生来决定要好得多.

2 优化课堂中的例题教学，提高课堂教学有效性

2.1 教学片段

教师：下面我们来看一个例题：

例题如图1，在矩形ABCD(AD>AB)中，点E、F分别在边AD、BC上，连接EF，EF垂直平分AC且与AC相交于点O.

图1

(1)求证：四边形AFCE是菱形；

(2)若AB=4 cm，BC=8 cm，求BF的长.

学生(众)：思考了约3分钟.(在学生思考的同时，教师不断“启发”着学生：要证明四边形AFCE是菱形，已经知道对角线互相垂直了，只要证明什么就可以了？……)

教师：好，下面我请一位同学说一说这道题他是怎么做的.

学生5：口述解题过程(说的基本正确).(教师板书)

教师：同学们说这位同学说的对不对？

学生(众)：对！

教师：现在同学们把解题过程完善一下.

……

2.2 教学反思

上面的例题讲解看起来很成功，教师给学生一定自主思考的时间，然后请一位同学来说如何解，这位同学也不负众望，说得很好，教师也板书了规范的解题过程并强调了要注意的地方.但笔者听完，总感觉少了点什么，脑子里想了几个问题：这位同学是怎么想到的呢？其他同学听懂了吗？其他同学是怎么想的呢？同学中有没有典型错误呢？众所周知，证明问题的关键在于找出正确的证明方法或途径，这是最困难的，也正是我们力求研究和解决的问题.但学生5只是回答了怎么做的，而没有说出是怎么找出正确的证明方法或途径的，也就是没有展现出分析过程.教师对此并没有追问的意思，甚至还庆幸找对了人.这样的例题教学会有多少效果呢？它对学生今后的解题有多少帮助呢？这值得我们深思.笔者认为以上的例题教学活动可以这样设计：先让学生自主思考，然后让学生谈自己的思考过程而不是解题过程，一个学生说完后教师不要急于评价，而是让学生评价，教师再对学生的评价给出评价，这样不仅能让学生说出分析过程，还能激发出更多的解题思路，激励更多的学生互动，让更多的学生参与到这一活动中来，让每一位学生都有所得.在学生充分弄清了解题思路后，书写证明过程就变得简单了.教师最后再对解题方法策略进行归纳小结就可以了.

当然，对例题进行变式教学也是提高课堂教学有效性的重要手段，教学时，可对此例进行适当变式.由于此例的重点是第一问，所以可以对此例作如下变式：

变式1已知：如图2，在梯形ABCD中，AD∥BC，点E、F分别在边AD、BC上，连接EF，EF垂直平分AC且与AC相交于点O.求证：四边形AECF是菱形.

图2

此变式题改变例题条件(弱化条件)，可以让学生认清使四边形AECF是菱形的条件是AD∥BC且EF垂直平分AC，加深对基本图形的认识，主要样可以提高学生的识图能力，从而提高学生的解题能力.

变式2已知：如图3，矩形ABCD中，E、F分别是边AD、BC边上的点，且AF=CE.当AC⊥EF时，求证：四边形AFCE是菱形.

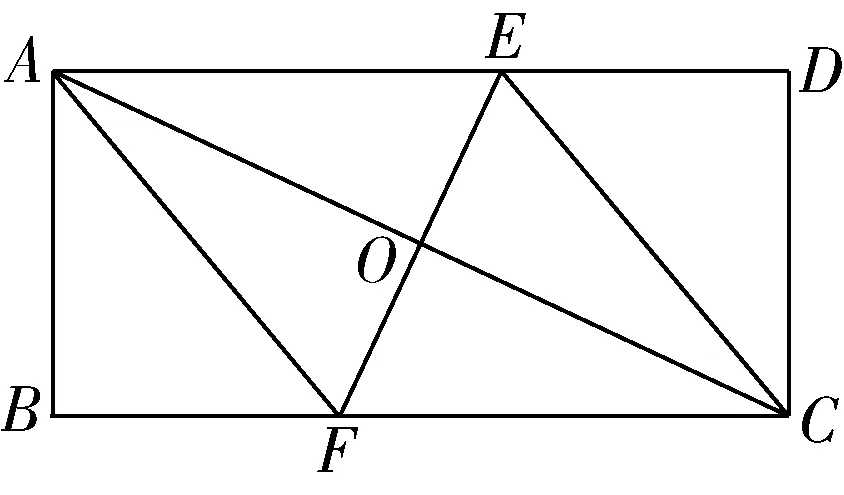
图3

此变式题改变例题条件(替换条件)，让学生借助上面的解题经验分析并解决问题，训练学生思维的灵活性.

图4

变式3已知：如图4，在△ABC中，AD平分∠BAC，AD的垂直平分线分别交边AB、AC于点E、F，连接ED、FD.

此变式题改变图形而不改变图形本质，让学生更好地看清图形结构，看透图形本质，提高解题能力.

这样的变式不仅能激发学生的学习兴趣和学习热情，加深学生对所学的定义和定理的理解，巩固新知，也有助于学生看透问题本质，归纳此类问题的一般解题方法，进而培养学生的思维转变能力与创新能力，提高学生的思维品质，提高初中数学教学的质量和效率.

3 优化课堂中的目标检测，提高课堂教学有效性

3.1 教学片段(例题教学结束后)

教师：同学们，今天这节课你们学到了什么？

学生：我学到了菱形的判定方法……

教师：很好，剩下的一点时间(约3分钟)，同学们做学案上的练一练……(教师看表等待下课)

3.2 教学反思

教师在例题教学之后就与学生互动，进行课堂小结，然后布置作业给学生做，学生在写作业过程中等待下课，这样的结尾看似干净利落，教师也感觉很轻松.但笔者感觉这样的课堂结尾似乎缺失了什么，对这堂课的教学效果也产生了怀疑.带着疑惑，笔者利用下课时间查看了部分学生的课后作业(各个层次的学生都有)，并和他们进行了简单的交流，发现学生对本堂课的内容掌握不太好，甚至有4位同学对菱形的几种基本判定方法都搞不清楚(作业第一题做错)，这除了因为本节课开头教师过多干预导致学生感悟较少外，还有一个重要原因就是教师没有对学情进行及时反馈，并没有真正以学生为本，导致教学效果大打折扣.

在此，笔者以为，用一份精炼的当堂检测来了解学情、及时补标很有必要.众所周知，当堂检测是实现有效课堂的一个重要环节，是提高数学课堂教学有效性的重要手段.通过当堂检测，不仅能及时了解最真实的学情，也能充分调动学生学习的积极性，同时又是教师走近学生，进行个别辅导的一个重要环节.因此，为了及时了解学生的课堂学习情况，发现问题及时纠正，有针对性的当堂检测必不可少.当堂检测应题量适当，难度适宜，时间为6分钟左右，例如，本节课的当堂检测可设置为：

当堂检测

1.下列命题中正确的是( ).

对比两组患者住院期间不良事件发生率（包含电解质失调、呼吸道堵塞、舌咬伤）、护理的总有效率，疗效判定标准：显效：经护理，患者意识、感觉障碍、抽搐等症状基本消失；有效：经护理，患者意识、感觉障碍、抽搐等症状发作次数减少50%；无效：经护理，患者意识、感觉障碍、抽搐等症状无明显改善，以有效加显效例数占总例数之比计量总有效率。

A.四个角相等的四边形是菱形

B.三条边相等的四边形是菱形

C.一组邻边相等的四边形是菱形

D.四条边相等的四边形是菱形

2.对角线互相垂直平分的四边形是( ).

A.矩形 B.一般的平行四边形

C.菱形 D.以上都不对

3.顺次连接矩形各边中点所形成的四边形是( ).

A.等腰梯形 B.矩形

C.菱形 D.正方形

4.如图5，在四边形ABCD中，对角线AC，BD相交于点O，AO=CO，BO=DO，添加下列条件，不能判定四边形ABCD是菱形的是( )

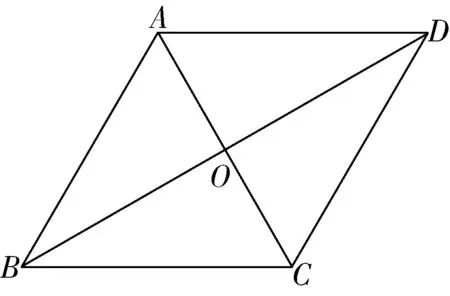
图5

A.AB=ADB.AC=BD

C.AC⊥BDD.∠ABO=∠CBO

5.如图6，将一张矩形的纸对折再对折，然后沿着图中的虚线剪开，将剪下的三角形打开后得到的图形是( ).

图6

A.矩形 B.菱形

C.正方形 D.等腰梯形

6.如图7，已知：四边形ABCD是平行四边形，甲、乙两人分别在四边形ABCD上作图如下：

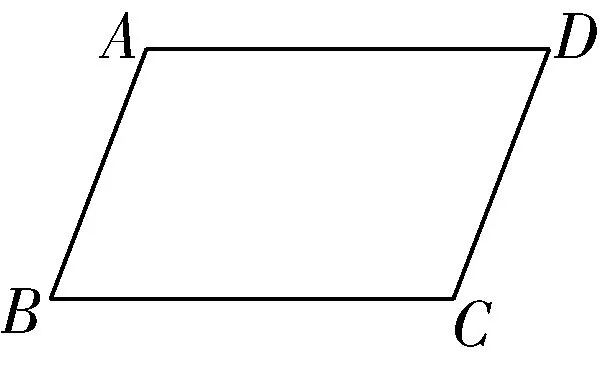
图7

甲：如图8，连接AC，作AC的垂直平分线分别交AD，BC，AC于点M，N，O，连接AN、CM，则所得四边形ANCM________(填“是”或“不是”)菱形；

乙：如图9，分别作∠A，∠B的平分线AE，BF，分别交BC，AD于点E，F，连接EF，则所得四边形ABEF________(填“是”或“不是”)菱形.

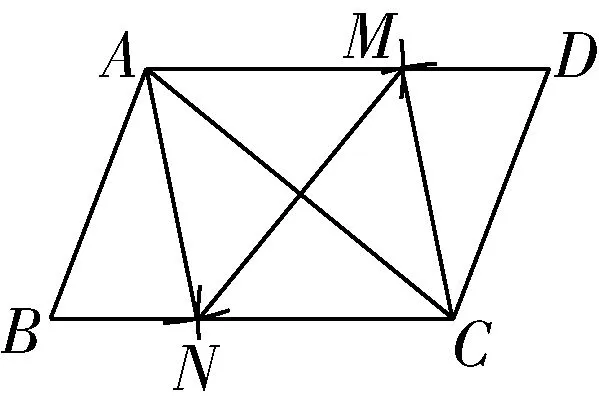
图8

图9

7.如图10，在△ABC中，点D是BC边上一点，过点D作DE∥CA、DF∥BA,分别交边AB,AC于点E、F.有下列三种说法：

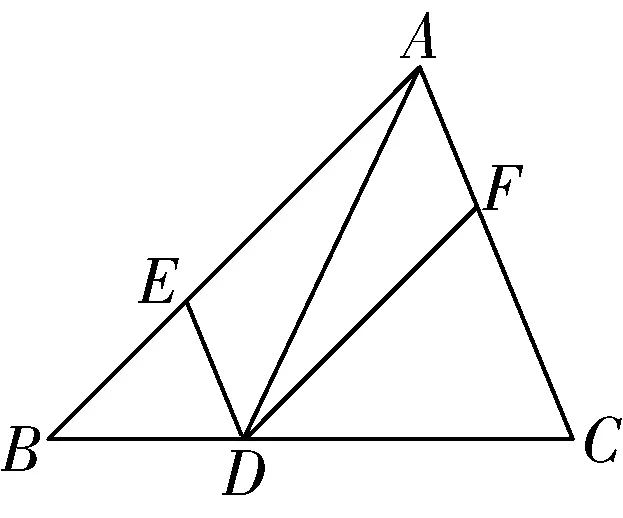
图10

①如果AE=AF，那么四边形AEDF是矩形；

②如果AD平分∠BAC，那么四边形AEDF是菱形；

③如果AD⊥BC且AB=AC，那么四边形AEDF是菱形.

其中，正确的有________.(填写序号)

选择你认为正确的一种说法说明理由.

8.如图11，在△ABC中，∠CAB=90°，AD是斜边BC的中线，E是AD的中点，过点A作BC的平行线，交BE的延长线于点F，连接CF.求证：四边形ADCF是菱形.

图11

检测题的设计要有梯度，以小题为主，要面向全体学生.学生在做当堂检测的同时教师可以适当巡批，了解学生的问题，对个别问题及时进行个别指导，共性问题集中讲解，及时纠正学生中存在的问题，加深学生对所学知识的理解.这样，对学生而言，不仅所学知识得到了巩固，而且对本节课的整体把握也更好，为后续的学习奠定基础.当然，这需要一定的时间，所以需要优化前面新授课部分的内容，为后面的当堂检测留足时间.

结 语

课堂是学生获取知识、训练思维、提高技能和形成思想方法的主阵地.课堂教学的有效性是提高教学质量的关键.新课标中指出，在教学活动中，教师要选择适当的教学方式，因势利导、适时调控，努力营造师生互动、生生互动、生动活泼的课堂氛围，形成有效的学习活动.

探究提高课堂教学有效性，我们都还在路上.有这样一种说法：“教学是一门遗憾的艺术.”我非常赞同.任何一堂课都会有缺憾，就算是经历多次打磨的公开课，也不可能完美无缺.我想，只要我们在新课程理念指导下，多思考，多研究，在发挥学生主体作用的前提下，立足课堂，关注学生，一定能找到更多的提高课堂有效性的方法和策略.