两段式喷嘴淹没空化射流流场数值模拟

董景明，李 帅，钟 萧，蒙荣轩

（大连海事大学 轮机工程学院，辽宁大连 116026）

0 引言

船舶在海洋中长时间航行后，浸没在海水中的船体表面被粘附有生物贝类、藻类植物等海生物所污损，这会增大船舶表面的粗糙度，最大可增加84%的船舶航行阻力，降低10%的航速，增加燃油消耗而排放更多的温室气体［1］。此外，已有研究表明船舶污底是入侵水生物转移的一个重要媒介［2］，会对当地的生态环境造成严重威胁。目前，清洗船舶海生物污垢的方式主要是坞内清洗、防污漆和定期水下清洗［3］。坞内清洗需要船舶进坞，通过人工和高压水射流清洗2种方式。人工刮铲存在清洗效率低，劳动强度大和清洁成本高等缺点。高压水射流清洗具有环保、清洗效率高、适用面广等优点。但实际清洗作业中，压力过小无法有效去除附着结实的海生物，压力过大会破坏船舶母材，且高压水射流清洗应用于水下工作时存在压力衰减严重等问题。防污漆通过喷涂在船体表面的防污涂层逐渐释放杀菌剂来有效杀死或减慢海生物生长。防污效果会随着涂料的老化大大降低，因此需要定期重新喷涂防污涂料。水下清洗船舶无需进坞，节约时间和清洗成本。现阶段水下清洗方式主要是靠潜水员手持刮铲、转刷进行船体表面清洗，效率低危险性高。空化射流清洗具有环保、高效、节能、安全性高等特点，被广泛应用于水下清洗［4］、切割［5］、材料测试［6］、地下钻井［7］等。

喷嘴作为空化射流发生的关键装置，其结构的改变会对空化效果产生显著的影响。如何进一步通过喷嘴结构优化提高空化效果，成为众多学者的研究热点。万春浩等［8］研究角形喷嘴的直径段直径大小对空化效果的影响，研究表明增大圆柱段直径会增强空化。孙鹏飞等［9］通过在亥姆霍兹喷嘴出口处添加扩张管结构来达到增强空化效果。WANG等［10］研究了亥姆霍兹喷嘴的结构和几何形状对自激振荡空化效应和能效的影响。HITOSHI［11］研究了各种类型的喷嘴几何形状对侵蚀速率的影响，结果表明在最佳冲距下侵蚀速率是侵蚀时间的函数，侵蚀速率取决于喷嘴的几何形状。LI等［12］研究了风琴管喷嘴出口角度对射流轴向压力振荡的影响，结果表明出口角度对轴向压力产生较大影响。同时研究表明，出口角会影响喷嘴出口形状和射流之间的相互作用，提高风琴管喷嘴的实际工作效率。CAI等［13］研究了不同喷嘴出口形状对空化侵蚀特性的影响，结果表明存在最佳的出口尺寸使侵蚀效果最佳。池本彻等［14］提出一种新型两段式喷嘴并成功使冷冻机系统COP提高了50%。其主要工作原理是液态制冷剂会在第一段喷嘴内产生气泡，随着喷嘴内面积增大压力提高，气泡会破裂产生气泡核，随后在第二段喷嘴中主引射制冷剂急速膨胀，液滴微粒化，达到液滴与气体流速相等的近似于匀质流状态的目的。郭宪民等［15-17］将两段式喷嘴改进应用于引射制冷系统中，系统的COP较传统系统最大提高达12.36%。

目前，两段式喷嘴的研究主要集中在引射制冷系统中，对于两段式喷嘴应用在空化射流领域的鲜有研究。为了验证两段式喷嘴的空化效果及结构参数改变对空化的影响，采用FLUENT对两段式喷嘴进行数值模拟。重点研究第一喉部直径、第二喉部直径和连接处直径对两段式喷嘴空化特性的影响。

1 物理模型

1.1 几何结构

本文所研究的两段式喷嘴结构是根据文献［14］设计优化后得到，如图1所示。喷嘴的具体结构参数见表1。

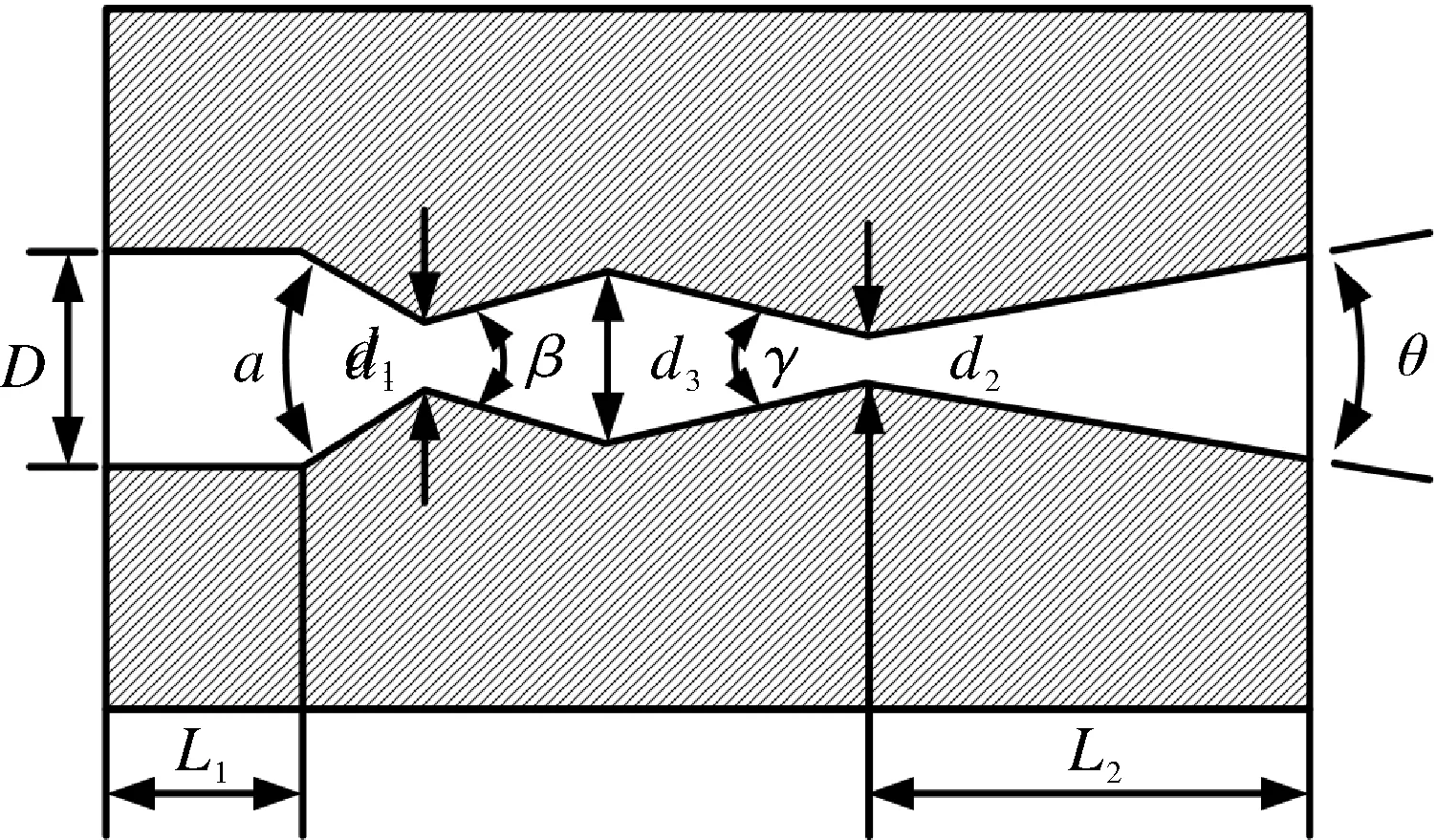
图1 喷嘴物理模型Fig.1 Physical model of nozzle

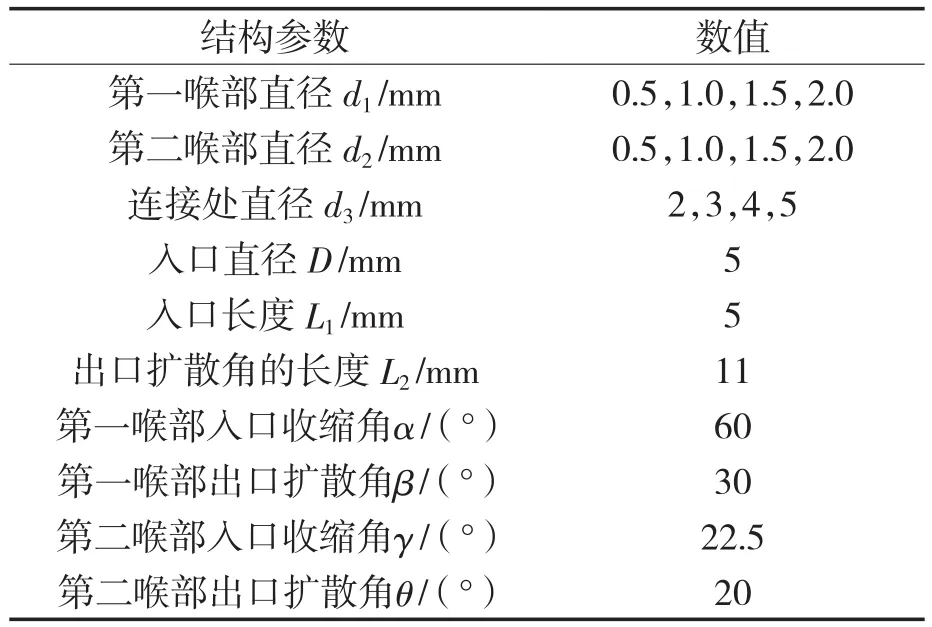
表1 两段式喷嘴的结构参数Tab.1 Structural parameters of dual-throat nozzle

1.2 网格划分与边界条件

由于喷嘴及外流场是对称结构，为了简化计算，物理模型采用二维结构，同时取二维结构的一半区域进行计算。为了获得稳定的流场流态，外流域大小设置为长70 mm，宽40 mm。网格的划分采用四边形结构化网格，喷嘴内部区域网格进行了加密，划分情况如图2所示。

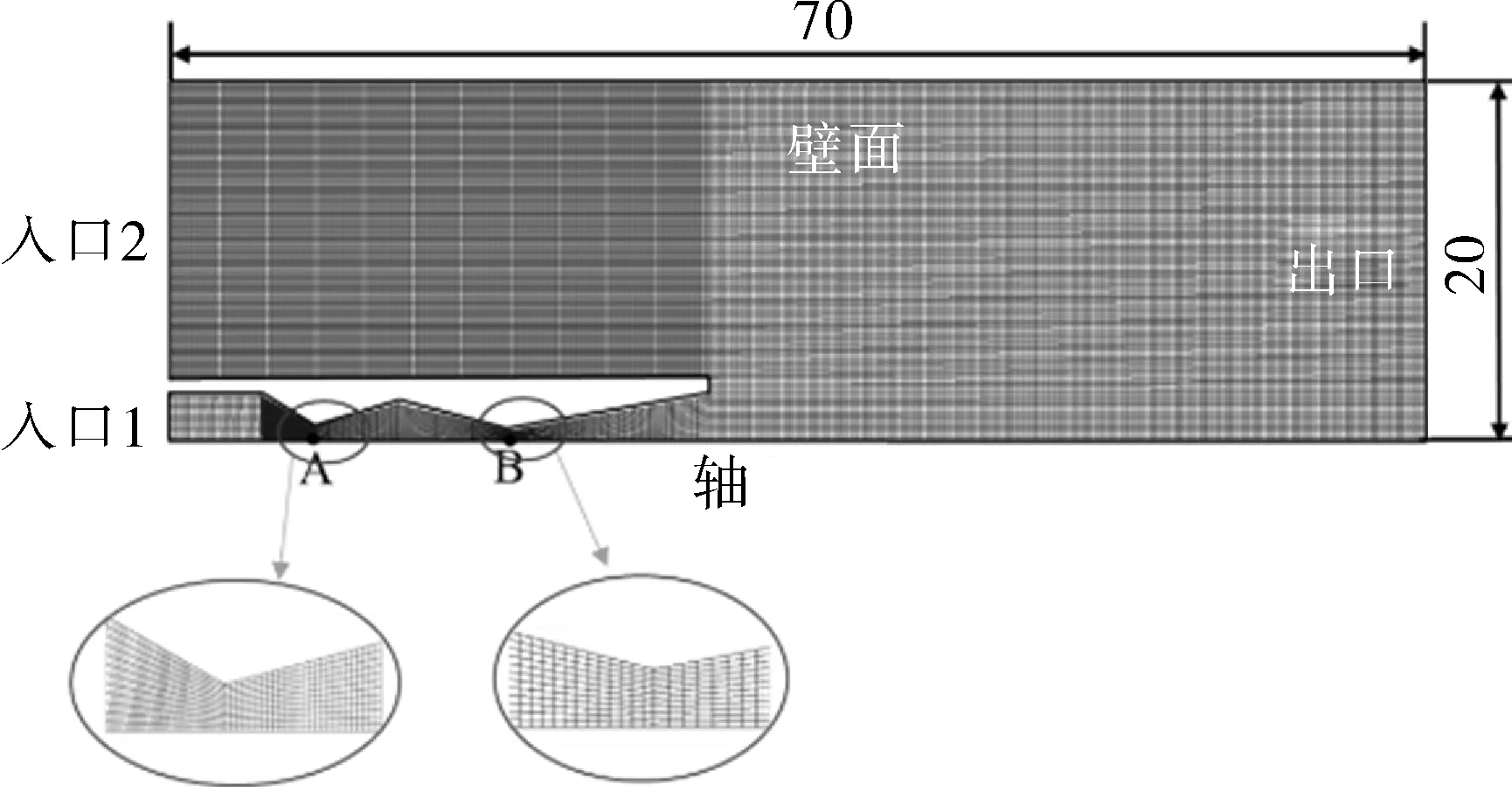
图2 网格划分Fig.2 The mesh division

为了减少计算误差，在第一喉部出口（点A）和第二喉部出口（点B）设置检测点，进行网格无关性检验。采用具有空化模型设置计算，分别采集点A和点B计算收敛后瞬时速度和压力值。表2和表3分别表示点A和点B处速度和压力随着网格数量变化而产生的误差，网格数量从25 914增加至142 137。从表1可以看出，随着网格数量的增加，速度和压力的误差也越来越小。在网格数量为104 732和142 137时，网格数量对速度和压力的影响可忽略不计，故本文网格计算的数量约为10万。

表2 网格无关性检验（点A）Tab.2 Mesh independence test（point A）

表3 网格无关性检验（点B）Tab.3 Mesh independence test（point B）

模拟边界条件设置：入口边界条件均为压力入口，设置空化喷嘴的入口压力为20 MPa，流场入口根据条件设置流场的环境压力。出口边界条件为压力出口，设置为一个大气压。固体壁面条件满足无滑移壁面条件，近壁面区域采用壁面函数处理。流场迭代求解方法选择SIMPLE，离散格式选择二阶迎风方程。由于空化发生是非定常过程，采用瞬态计算，计算时间步长ΔT=0.000 001 s，计算结果要求所有残差值小于10-6。

1.3 数学模型

空化射流属于气液两相流，同时也属于湍流流动，因此采用多相流中的混合模型、空化模型和湍流模型对空化射流流场进行模拟。

1.3.1 混合模型

混合模型针对整个混合流场系统且可以联合空化模型使用求解，具有准确性高，资源占用率小，且计算速度较快等优点，符合空化射流流场中对空化特性计算要求。其包括连续性方程式和动量方程式：

1.3.2 湍流模型

RNG k-ε具有良好的捕获剪切层末端小漩涡的能力，并且可以覆盖从低雷诺数到高雷诺数的大范围脉动区域，在空化喷嘴流场中具有较好的效果［18］。

式中 k ——湍动能，m2/s2；

ui——流场中i方向流体速度，m/s；

xi——流场中i方向空间变量；

αk，αε—— 湍动能 k 和耗散率ε对应的普朗特数，αk= αε=1.39；

ε ——湍动能耗散率，m2/s3；

C1ε，C2ε——经验常数。

1.3.3 空化模型

Schnerr-Sauer模型具有更高的计算精度和更好的收敛性。该模型通过耦合气相体积分数、气泡数密度进行求解，其定义相间质量输送率为：

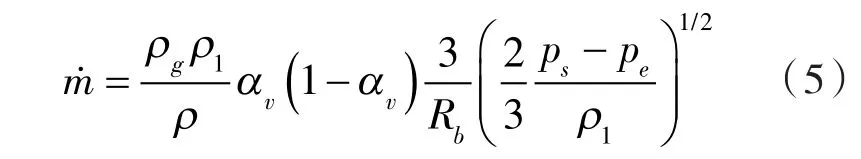
式中 ρg，ρ1，ρ —— 气 相、液 相 和 混 合 相 密 度，kg/m3；

αv——气体体积分数；

Rb——气泡半径，m；

ps，pe——饱和压力和环境压力，Pa。

1.4 模拟结果验证

为验证模拟结果的可靠性，将喷嘴结构参数为第一喉部直径d1=1.5 mm，第二喉部直径d2=1.0 mm，连接处直径d3=1.5 mm的数值模拟结果与高速摄影结果对比，对数值计算方法和精度进行验证。图3所示为喷嘴数值模拟和高速摄影空泡云图对比。从模拟结果可以看出，淹没空化射流的空泡云具有明显的周期性，空泡云呈间断团状分布于喷嘴出口，随后在湍流的作用随流场发生扩散和破碎。数值模拟结果与实验现象基本一致，且空泡云尺寸和发展周期较为接近，因此可以验证数值模拟结果的可靠性。

图3 数值模拟与高速摄影空泡云形态对比Fig.3 Comparison of cavitation cloud morphology between numerical simulation and high-speed photography

2 结果与讨论

因空化发生属于非定常过程，为了更好地分析结构参数对空化效果的影响，选取同一时刻下瞬态物理量进行分析。通过对喷嘴内外流场速度、湍动能以及气相体积分数的分析，得到了不同第一喉部直径、第二喉部直径和连接处直径对喷嘴流场的影响规律。同时为了验证两段式喷嘴的空化效果，通过模拟与空化效果较好的角形喷嘴进行了对比研究。

2.1 第一喉部直径对空化射流的影响

在第一喉部直径分别为 0.5，1.0，1.5，2 mm，第二喉部直径为1.0 mm，连接处直径为4 mm时，研究第一喉部直径对空化射流效果的影响。

图4示出不同第一喉部直径时两段式喷嘴的气相分布云图，当d1=0.5 mm时，空化率先发生在喷嘴第一喉部处，空化区域主要集中在连接腔内，同时在喷嘴扩散段出现少量空化泡。为了解释这一现象，对图5（a）速度分布云图进行分析，在d1=0.5 mm时第一喉部出口处达到速度最大值并开始形成射流核心区，轴线处速度增加加剧了壁面附近流体的扰动，使得壁面附近形成低压区。当压力低于流体在该温度下的饱和蒸汽压，空化泡开始大量出现。随着第一喉部直径d1的增加，空化首先发生在第二喉部处，在靠近喷嘴出口处空泡云主要沿着剪切层的边界分布。如图6示出不同第一喉部直径时两段式喷嘴的气相体积分数曲线。图中纵坐标表示蒸汽气相体积分数，横坐标表示从喷嘴入口至流场出口轴线长度。由图中可以看出，随着第一喉部直径的增大，喷嘴的空化性能和空化影响区域先增加后减小，在d1=1.5 mm时，轴心处的最大体积分数为0.9，此时空化的区域范围达到最大。

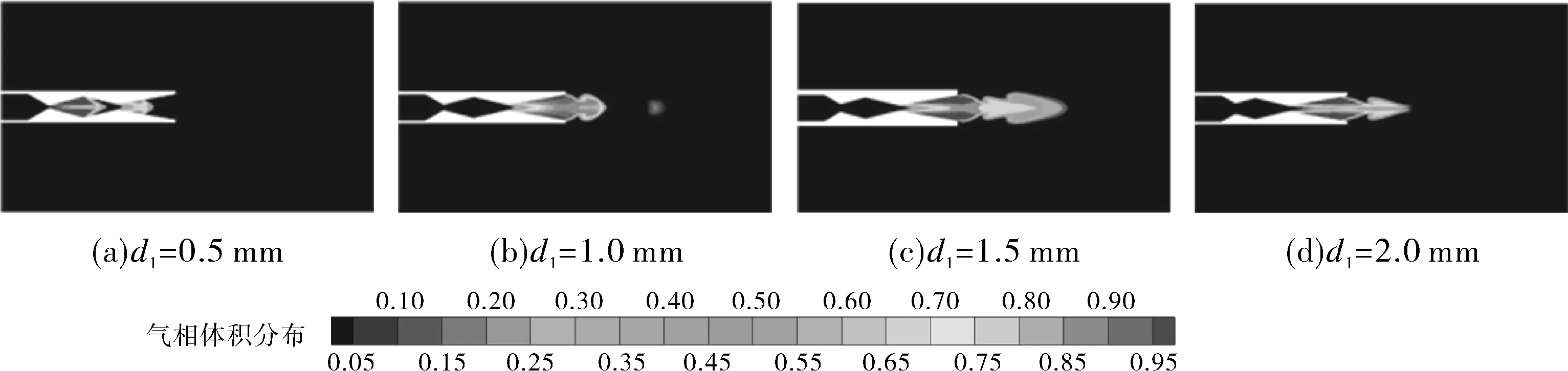
图4 不同第一喉部直径时两段式喷嘴的气相分布云图Fig.4 Vapor volume distribution nephogram of two-stage nozzle with different first throat diameters

图5 不同第一喉部直径时两段式喷嘴的速度分布云图Fig.5 Velocity distribution nephogram of two-stage nozzle with different first throat diameters

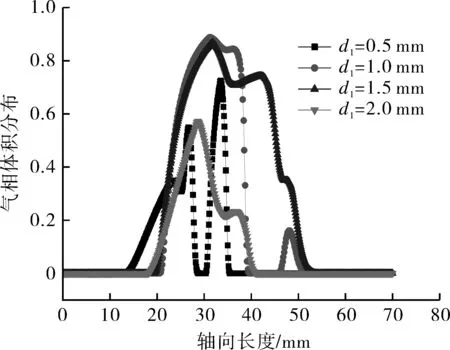
图6 不同第一喉部直径时两段式喷嘴的气相体积分数曲线Fig 6 Vapor volume fraction curves of two-stage nozzle with different first throat diameters

图7示出不同第一喉部直径时两段式喷嘴的湍动能分布云图。从图中可以看出，当d1=0.5，1.0 mm时，湍动能的峰值分别为1 480，801 m2/s2，且峰值区域主要集中在连接腔内。随着第一喉部直径的增大，湍动能较高区域分布在径向线两侧且逐渐向喷嘴出口移动，与空化分布区域相似。由于空化发生时，空泡产生和溃灭时流场会出现强烈扰动，特别是空泡溃灭时会产生瞬时的高压，这使得流场内的脉动压力增大，湍动能也会急剧增加，因而湍动能的变化情况也可反应出空化的强弱。

图7 不同第一喉部直径时两段式喷嘴的湍动能分布云图Fig.7 Turbulent kinetic energy distribution nephogram of two-stage nozzle with different first throat diameters

由此可见，第一喉部直径对空化效果产生很大影响，根据伯努利原理，液体在流经第一喉部时会由于直径缩小导致静水压力降低产生气泡。随着喷嘴内的面积增大压力升高，气泡破裂形成气泡核随流向下游移动，气泡核是的存在是液体空化的先决条件，第一喉部直径的大小影响气泡核的形成，直接影响着空化效果。

2.2 第二喉部直径对空化射流的影响

在第一喉部直径为1.5 mm时，第二喉部直径分别为 0.5，1.0，1.5，2.0 mm，连接处直径为4 mm时，研究第二喉部直径对空化射流效果的影响。

图8示出不同第二喉部直径的气相分布云图。由图中可以看出，当第二喉部直径d2=0.5 mm时，在喷嘴出口附近形成的空化气泡云较小，轴向长度过短，主要原因是第二喉部直径过小导致流量小，从而减小了高速水射流与静水的剪切层，负压区变小。但空化发生的程度较为剧烈且集中，轴心处的气相最大气相体积分数达到了0.92。从湍动能分布云图9（a）中也可以看出，当d2=0.5 mm时，湍动能的峰值最高且峰值的位置位于喷嘴出口附近，说明此处空泡溃灭的最为强烈，空化发生的剧烈，同时也说明空化作用距离小。

图8 不同第二喉部直径时两段式喷嘴的气相分布云图Fig.8 Vapor volume distribution nephogram of two-stage nozzle with different second throat diameters

图9 不同第二喉部直径时两段式喷嘴的湍动能分布云图Fig.9 Turbulent kinetic energy distribution nephogram of two-stage nozzle with different second throat diameters

图10示出不同第二喉部直径下速度分布云图。结合图10（d）分析，当d2=2.0 mm时，在第一喉部出口处就开始出现空化，空化发生的位置集中在连接腔和扩散段壁面处。这是因为在第一喉部处形成等速核，等速度核持续到扩散段出口，由于速度梯度的存在形成剪切效应产生漩涡，漩涡涡核因角速度较大引起局部压力降低而产生空化。图11示出不同第二喉部直径的气相体积分数曲线。从图可以看出，随着第二喉部直径由0.5 mm增加2.0 mm时，轴心处最大气相体积分数不断减小。

图10 不同第二喉部直径时两段式喷嘴的速度分布云图Fig.10 Velocity distribution nephogram of two-stage nozzle with different second throat diameters

图11 不同第二喉部直径时两段式喷嘴的气相分布曲线Fig.11 Vapor volume fraction curves of two-stage nozzle with different second throat diameters

在d2=1.0 mm时轴心处最大体积分数为0.88，由于喷嘴直径的增大流量逐渐增加，增强了高速射流与静止伴随流的剪切作用区域和强度，因此此时空化区域最大。当d2=2.0 mm时轴心处最大气相体积分数下降到0.028 6，这是由于第二喉部直径过大时，射流从喷嘴流出后极易向四周扩散，导致射流能量快速扩散。对比湍动能分布云图图9（d）可以发现，湍动能的峰值为981 m2/s2，进一步说明在喷嘴出口处能量耗散较大。

由以上分析可知，第二喉部直径是影响空化射流性能的关键参数，在第二喉部处压力突降至低于该温度的饱和蒸汽压。此时流体处于拉伸状态，空化核在拉伸作用下得以发育成空泡，空化发生。所以可以通过改变第二喉部直径大小来增大压降，诱导液体中大量填满空穴的微气泡高速生长，提高空化的能力。

2.3 连接处直径对空化射流的影响

在第一喉部直径为1.5 mm时，第二喉部直径为 1.0 mm，连接处直径分别为 2，3，4和5 mm时，研究连接处直径对空化射流效果的影响。

图12示出不同连接处直径时两段式喷嘴的速度分布云图。由图可以看出，在相同入口压力20 MPa下，不同连接处直径下喷嘴轴线的最大速度为200 m/s，流体最大流速的流动距离约为30 mm，等速度核的大小相似。等速度核是对流场扰动影响和产生低压区的关键，故连接处直径对速度大小和分布区域没有明显影响。

图12 不同连接处直径时两段式喷嘴的速度分布云图Fig.12 Velocity distribution nephogram of two-stage nozzle with different connection diameters

图13为不同连接处直径时两段式喷嘴的湍动能分布云图。由图可以看出，在d3=2，3，4，5 mm湍动能的峰值分别为 825，820，731，648 m2/s2，湍动能峰值发生的位置均位于喷嘴的外流场中。随着连接处直径的增加，湍动能的峰值不断减小。主要原因是当连接处直径取值较小时，在连接腔内并未发生能量的耗散。当连接处直径取值较大时，在连接腔内发生能量损失。

图13 不同连接处直径时两段式喷嘴的湍动能分布云图Fig.13 Turbulent kinetic energy distribution nephogram of two-stage nozzle with different connection diameters

图14示出不同连接处直径时两段式喷嘴的气相分布云图。由图可以看出，喷嘴扩散段及出口附近形成的空泡云成对称分布。当d3=4，5 mm时，在空化区域的形态上和影响范围上的流场大致相同。

图14 不同连接处直径时两段式喷嘴的气相分布云图Fig.14 Vapor volume distribution nephogram of two-stage nozzle with different connection diameters

图15示出不同连接处直径时两段式喷嘴的气相体积分数曲线。由图可以看出，当d3=2 mm增加到d3=3 mm时，轴线上的最大气相分数由0.613增加到0.659，增长了7.50%，空化效果提升并不明显。当d3=3 mm增加d3=4 mm时，轴线处的最大气相体积分数达到了0.868，较d3=3 mm时增长了31.71%，空化性能有了显著提高。当d3=5 mm时，轴线处最大气相体积分数为0.875，与d3=4 mm时相比空化效果基本上没有变化。随着连接处直径的不断增加，空化影响范围也在随着增加。主要原因是当连接处的直径取值较小时，影响喷嘴气泡的产生及气泡破裂形成气泡核，从而影响空化效果；当连接处的直径d3大于4 mm时，连接处直径取值对空化效果几乎没有影响。

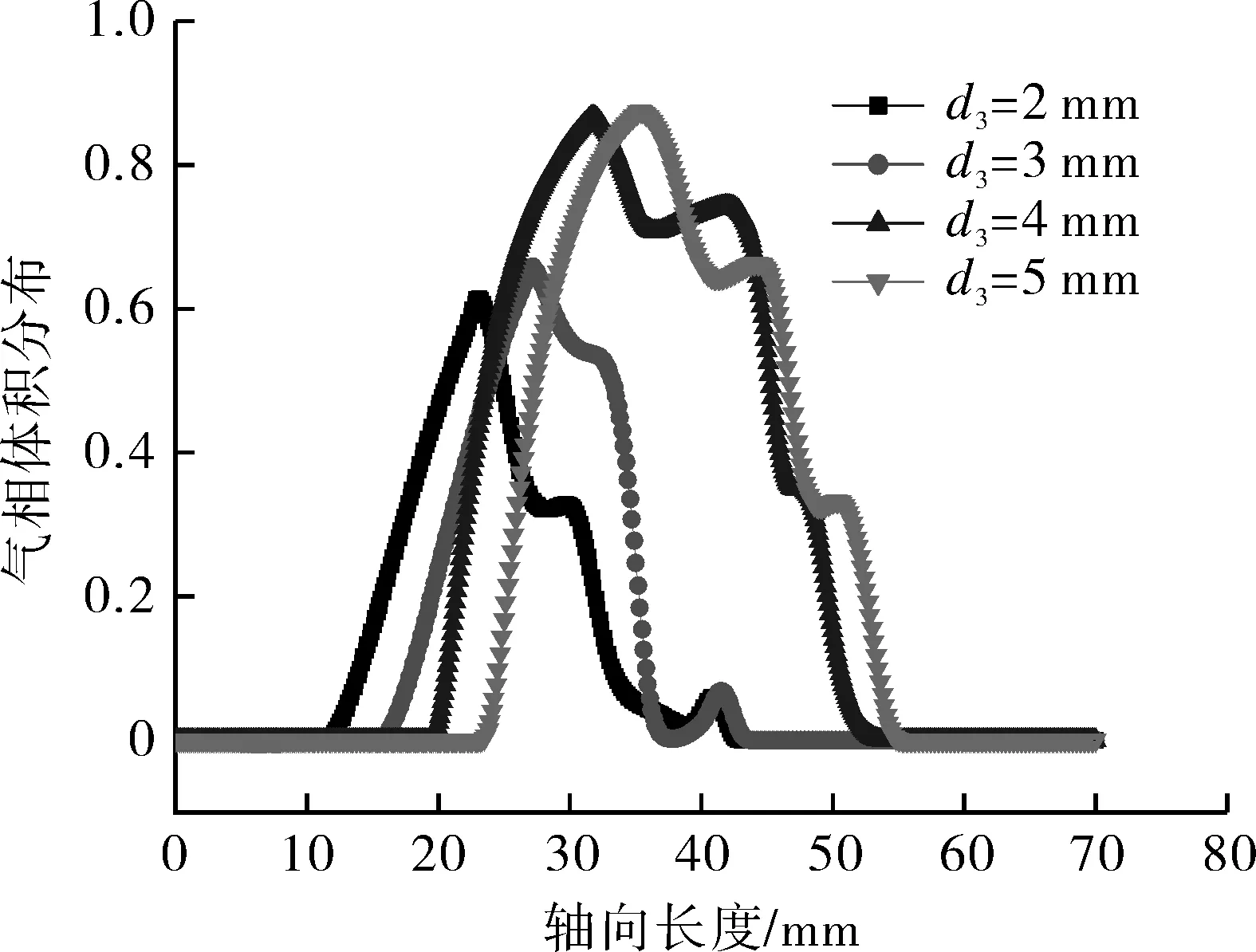
图15 不同连接处直径的气相体积分数曲线Fig.15 Vapor volume fraction curves of two-stage nozzle with different connection diameters

2.4 对比研究

为了验证两段式喷嘴的空化效果，在相同工况下，将本文提出的两段式喷嘴在第一喉部直径为1.5 mm，第二喉部直径为1.0 mm，连接处直径为4 mm时与文献［19］的角形喷嘴，进行了空化特性的对比分析。角形喷嘴的结构示意如图16所示。

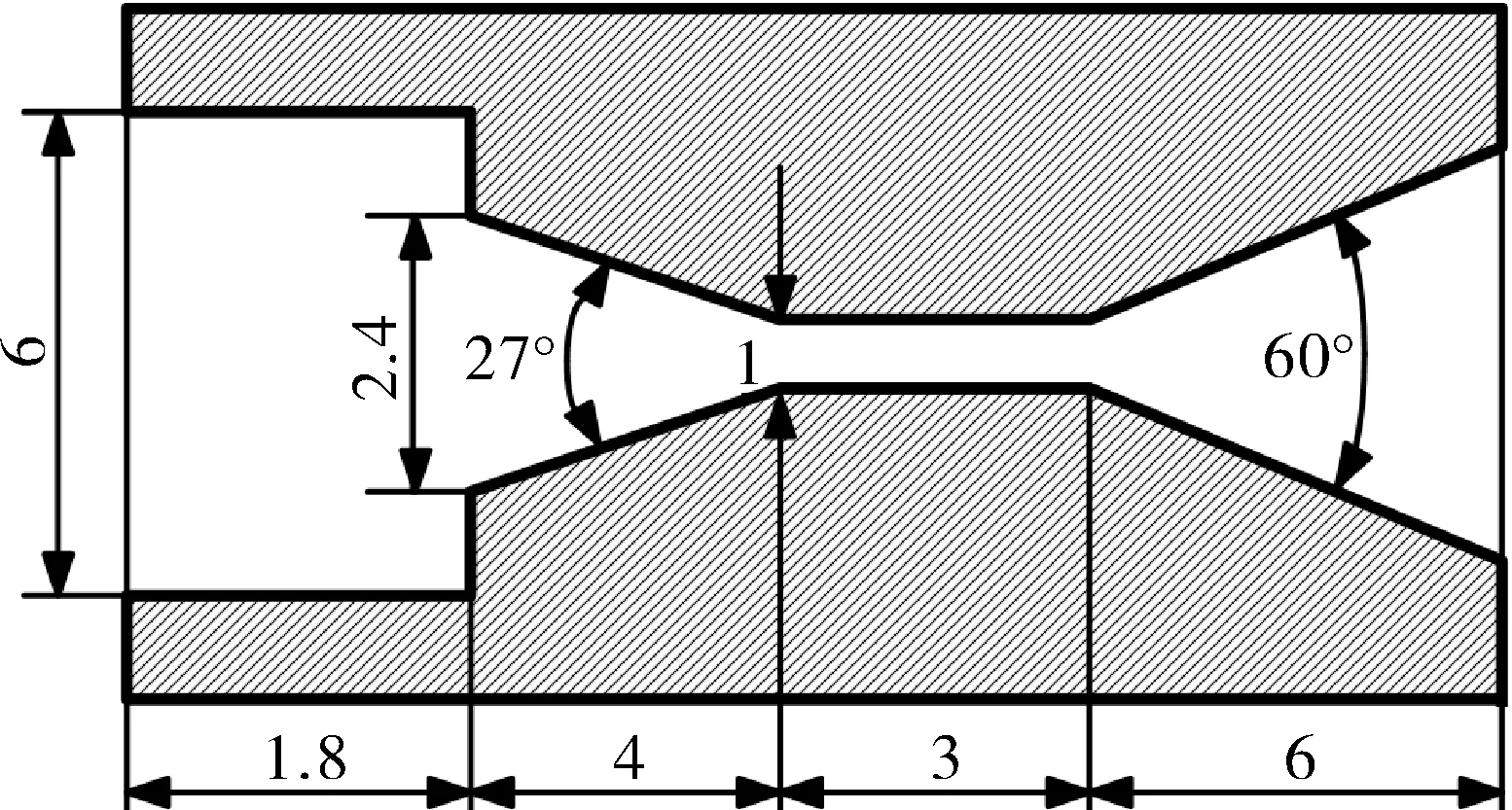
图16 角形喷嘴的结构示意Fig.16 Structural diagram of angle nozzle

图17示出两喷嘴轴线上速度对比，由图中可以看出，两喷嘴在相同的入口压力下，轴线上喷嘴出口的最大速度均为200 m/s，等速度核的长度基本相同。图18示出两喷嘴轴线上的气相体积分数对比。由图可以看出，两喷嘴轴线上的最大气相体积分数都是呈现先增加后减小的趋势。两段式喷嘴的空化影响的区域长度32 mm要大于角形喷嘴18 mm，角形喷嘴和两段式喷嘴轴线上的最大体积分数分别为0.723和0.868。通过对比可以发现，两段式喷嘴具有良好的空化效果。

图17 两喷嘴轴线速度比较Fig.17 Comparison of axial velocity between two nozzles

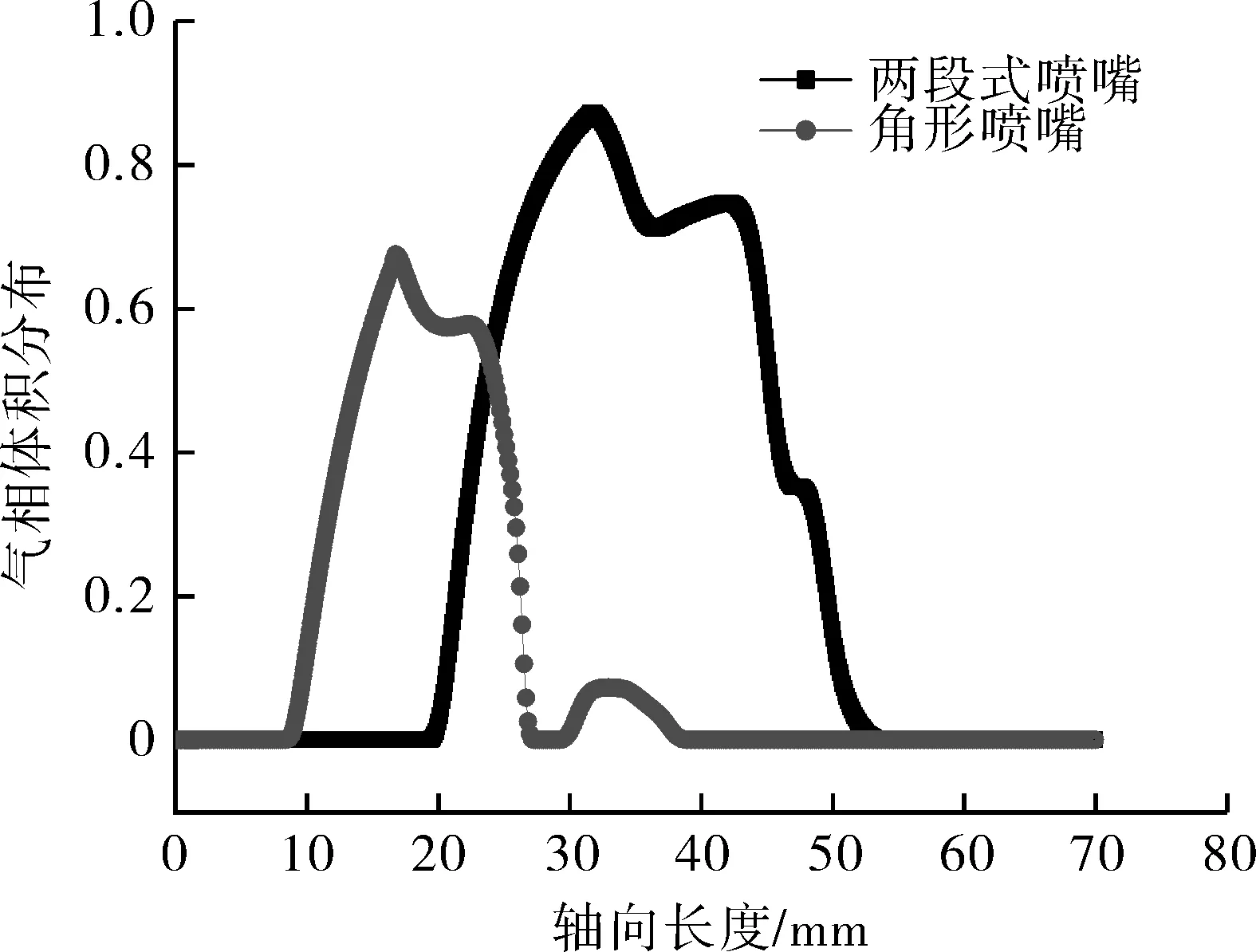
图18 两喷嘴轴线气相体积分数比较Fig.18 Comparison of vapor volume fractions of two nozzle axes

3 结论

当第一喉部直径取值过小时，空化仅发生连接腔内。随着第一喉部直径的增大，空化发生的位置后移。在d1=1.5 mm时，空化的区域达到最大，空化强度增强，轴心处的最大体积分数达到0.9。

第二喉部直径的取值越小，空化的程度越高，随着第二喉部直径的增大，空化程度有所减小但空化区域的区域变大。当d2=2 mm时，在第一喉部处就已经发生空化且空化的区域贴近壁面，在对称轴处的空化程度较低，故d2的值不宜过大。当d2=1 mm时，空化效果最好。

当连接处的直径取值较小时，影响喷嘴气泡的产生及气泡破裂形成气泡核，从而影响空化效果；随着连接处直径的增大，空化效果逐渐增强。但当连接处的直径d3大于4 mm时，连接处直径取值对空化效果几乎没有影响。

在相同工况下与角形喷嘴进行对比研究，验证两段式喷嘴具有良好空化效果。