基于快速密度峰值聚类离群因子的离群点检测算法

张忠平，李森，刘伟雄，刘书霞

（1.燕山大学信息科学与工程学院，河北 秦皇岛 066004；2.河北省计算机虚拟技术与系统集成重点实验室，河北 秦皇岛 066004；3.河北省软件工程重点实验室，河北 秦皇岛 066004；4.河北科技师范学院，河北 秦皇岛 066004）

0 引言

离群点指的是数据集中偏离正常数据分布的数据，它们的观测值与其他观测值有着显著的不同。离群点检测就是在数据集中发现离群点的过程，是数据挖掘中重要的研究方向。目前，离群点检测已应用在很多领域，如工业无线传感器网络[1]、欺诈检测[2-3]、入侵检测[4]、心电图异常检测[5]等。研究者对离群点检测也提出了很多算法，主要有基于统计的算法[6-7]、基于距离的算法[8-9]、基于聚类的算法[10-12]和基于密度的算法[13-18]等。

自 Breunig 等[13]提出局部离群因子（LOF,local outlier factor）算法后，基于密度的离群点检测算法已成为离群点检测研究领域最热门的方向之一。该类算法的核心思想是通过密度估计算法来计算各数据对象的密度，根据数据对象所处的区域来判断离群点，离群点通常处于稀疏区域，离群点的密度相较于正常数据对象而言有明显差异。近年来，随着聚类方法的发展，基于聚类的离群点检测算法已成为离群点检测研究领域不可或缺的一部分。其核心思想是对数据集进行聚类，离群点通常处于那些仅包含极少数据对象的小规模集群中。从核心思想上可以看出，上述2 类算法具有一定的相似性，小规模的集群往往也是稀疏区域。这2 类算法有各自的优缺点，近几年研究者开始把研究重心放在如何结合两者的优点上，从而提出一种具有更强稳健性的离群点检测算法。

Rodriguez 等[19]提出了一种具有重要价值的新型聚类算法——密度峰值聚类（DPC,density peak clustering）算法。DPC 算法是一种简单高效的聚类算法，可以通过计算局部密度以及相对距离，将任意维度的数据集映射成一个二维的决策图，决策图可以清晰地反映数据集的层次关系；然后选取数据集中密度高且距离其他高密度数据对象较远的数据对象作为数据集的聚类中心，这些数据对象称为密度峰值点；最后将剩余的数据对象分配到距离其最近的聚类中心。相较于其他传统聚类算法，DPC算法受离群点和噪声的影响较小，另外，DPC 算法在聚类的过程中不需要多次迭代，因此，不管是从检测精度还是从时间效率层面考虑，DPC 算法更适合与离群点检测算法相结合。

尽管DPC 算法可以简单高效地完成聚类，但仍存在一些问题。首先，由于DPC 算法需要计算各数据对象密度，计算过程中会产生距离矩阵，在增加空间复杂度的同时也增大了时间复杂度，DPC算法的时间复杂度为O(n2)，对于一些大规模数据集，其时间效率会严重下降。文献[20]提出了基于网格的密度峰值聚类（DPCG,density peak clustering based on grid)算法，在计算数据对象的局部密度时采用网格思想计算距离的方法来代替DPC 算法中计算数据对象之间距离的方法，从而提高了算法计算速度。其次，DPC 算法在初始时需要设置截断距离dc且需要人工选择聚类中心，由于算法对于截断距离dc非常敏感，人工设置容易导致算法精度下降。Huang 等[21]提出自适应密度峰值检测的快速聚类算法，该算法采用非参数的高斯核密度估计代替DPC 算法中的密度估计，不需要设定截断距离dc，还提出了一种基于轮廓优化算法的聚类中心选择方法来自动选择聚类中心，但该方法在面对一些稀疏且小规模的簇类数据集时，难以保持正常的精度。

本文针对DPC 算法时间复杂度高、截断距离的设定和聚类中心选取的问题进行了改进，并将改进的DPC 算法与离群点检测相结合，提出了基于快速密度峰值聚类离群因子（FDPC-OF,fast density peak clustering outlier factor）的离群点检测算法，简称FDPC-OF 算法。本文算法主要分为2 个阶段进行工作。第一阶段，使用改进的DPC 算法计算聚类中心；第二阶段，基于聚类中心定义了向心相对距离，从而提出基于快速密度峰值聚类离群因子（简称FOF）来刻画数据对象的离群程度。本文的主要贡献总结如下。

1) 本文算法采用 k 近邻（KNN,k-nearest neighbour）算法代替DPC 算法中密度估计的部分，避免了设定截断距离dc，并使用k 维树（KD-Tree,k-dimensional tree）索引数据结构计算各数据对象的k 近邻，降低算法的时间复杂度。

2) 使用局部密度与相对距离的乘积来自动选择聚类中心，避免人为选取聚类中心。

3) 对DPC 算法中的相对距离进行改进，定义了平均向心距离，并结合数据对象的相对距离以及平均向心距离定义了向心相对距离，结合向心相对距离和局部密度这2 个指标，提出了基于快速密度峰值聚类离群因子来刻画数据对象的离群程度。

1 相关工作

1.1 密度峰值聚类DPC 算法

经典的聚类算法K-means[22]通过指定初步聚类中心再进行迭代更新找到最终聚类中心，由于每个点都被分配到距离最近的聚类中心，导致其不能检测非球面类别的数据分布。Ester 等[23]提出了DBSCAN（density-based spatial clustering of application with noise）算法，可以对任意形状分布的数据进行聚类，但是必须指定一个密度阈值，从而去除低于此密度阈值的噪声点。Comaniciu 等[24]提出了MeanShift 算法，采用均值偏移的方式使数据点向密度较大的方向延伸，直至收敛到簇中心。但是均值偏移是一个不断迭代的过程，时间复杂度较高。DPC 算法解决了以上不足，其原理简单，要求参数少，不需要迭代，并且能够识别不同形状大小的簇。

DPC 算法的核心思想是基于一种假设，即在任意数据分布的数据集中，聚类中心通常会被具有较低局部密度的数据对象所包围，并且这些聚类中心与其他具有较高局部密度的数据对象之间的距离都相对较大。在这个假设的基础上，DPC 算法需要计算2 个指标，一个是数据对象的局部密度，另一个是数据对象的相对距离，这2 个指标都需要通过数据对象之间的距离dij计算得出；然后，根据局部密度和相对距离来构建聚类中心决策图，以此选择聚类中心；最后，将数据集中剩余的数据对象分配到距离其最近的聚类中心，完成聚类。

定义1密度峰值聚类局部密度ρi[19]。ρi指数据对象xi在截断距离内包含的其他数据对象的个数。其计算式如下

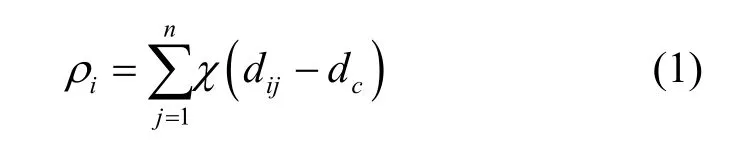
其中，n为数据集中数据对象的个数；dij为数据对象xi和xj之间的欧氏距离；截断距离dc需要在算法开始时进行初始化设置；χ(·)为指示函数，若x＜0，χ(x)=1，若x≥ 0，则χ(x)=0。简单来说，截断距离dc类似于半径，ρi则是通过指示函数计算在半径范围内其他数据对象的个数。

定义2密度峰值聚类相对距离δi[19]。δi指数据对象xi与其他局部密度比它大的数据对象的最短距离。其计算式如下

对于ρi最大的数据对象，通常将它的δi设置为其与最远的对象之间的距离，即δi=maxj(dij)。值得注意的是，当xi为DPC 局部或者全局密度最大值时，DPC 相对距离会大于传统的k 近邻距离，因此聚类中心的DPC 相对距离会是非常大的值。

计算局部密度和相对距离后，DPC 算法根据这2 个指标构建聚类中心决策图，以此选择聚类中心，该决策图的观测过程是DPC 算法的核心。由28 个数据对象生成的DPC 二维数据分布如图1 所示。从图1 可以发现，1 号和10 号数据对象分别位于各自簇内的密度峰值区域，因此将其作为聚类中心。

图1 DPC 二维数据分布

由DPC 局部密度和DPC 相对距离所构建的DPC 决策图如图2 所示，从图2 可以发现，首先，虽然9 号和10 号数据对象的DPC 局部密度非常接近，但它们在决策图中所处的位置有非常大的区别，这是由于10 号数据对象在其所在簇中的DPC局部密度为最大值，DPC 局部密度比其大的数据对象位于另一个簇中，而9 号数据对象并非其所在簇中DPC 局部密度的最大值，因此10 号数据对象的DPC 相对距离比9 号要大得多，更加符合DPC 算法对聚类中心的假设；其次，由于1 号数据对象为DPC 局部密度的最大值，因此通过该决策图可以轻松选择出1 号和10 号这2 个聚类中心；最后，26～28 号数据对象具有较高的相对距离和较小的DPC局部密度，此类型的数据对象通常作为离群点单独成簇。

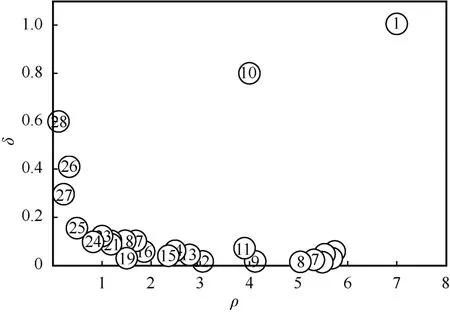
图2 DPC 决策图

通过决策图完成聚类中心的选定后，DPC 算法将数据集中剩余的数据对象分配到距离其最近的聚类中心所在的簇中完成聚类。DPC 算法如算法1所示。需要特别注意的是，聚类数目c和聚类中心需要通过决策图来人工选定。

算法1密度峰值聚类DPC 算法

输入初始数据集D和截断距离dc

输出c个聚类

1) for eachx∈Ddo

2) 计算x与其他数据对象之间的欧氏距离

3) end for

4) for eachx∈Ddo

5) 采用式(1)和截断距离dc计算x的DPC 局部密度

6) end for

7) for eachx∈Ddo

8) 遍历数据集D

9) 采用式(2)计算x的DPC 相对距离

10) end for

11) 根据计算得出的DPC 局部密度和DPC 相对距离构建二维决策图

12) 根据决策图人工选取聚类中心以及聚类数目c

13) 将数据集中剩余的数据对象分配至距离其最近的聚类中心

14) 完成聚类并输出c个聚类

1.2 k 近邻

定义 3k 近邻距离（KNN-dist,k-nearest neighbours distance）di。di是指xi到其KNN 内所有数据对象的平均距离。其计算式如下

其中，KNNi为数据对象xi的k 近邻的集合；dist(xi，xj)为数据对象xi和xj之间的距离，通常采用欧氏距离。

定义4KNN 局部密度deni[25]。deni是根据xi的KNN 距离构造的局部密度估计度量指标。其计算式如下

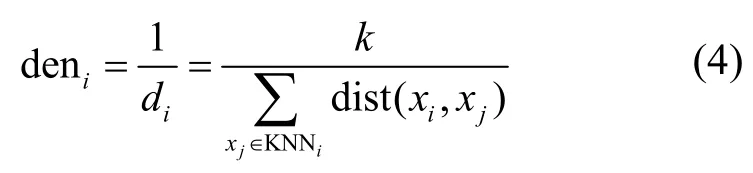
简单而言，数据对象xi的KNN 局部密度deni等于其KNN 距离di的倒数。

计算数据对象的KNN 距离时，需要先计算各数据对象之间的欧氏距离，时间复杂度高达O(n2)。当面对大规模数据集时，算法的时间效率会随着数据集的增大而快速下降。为了提高算法在大规模数据集上的适用性，本文采用KD-Tree 索引数据结构来优化KNN 距离的计算过程，首先对数据集进行建模，构建KD-Tree；然后，根据该KD-Tree 获取近邻样本数据。通过采用KD-Tree 索引结构来计算数据对象的KNN 距离，能将算法的时间复杂度优化至O(nlogn)。

2 FDPC-OF 算法

2.1 快速密度峰值聚类算法

针对DPC 算法中需要初始化设置截断距离参数以及需要人工选定聚类中心的问题，本文提出采用KNN 局部密度代替DPC 算法中局部密度估计，从而避免了人工设置截断距离参数，解决了DPC算法对于截断距离参数敏感的问题；并且使用局部密度与相对距离的乘积这一指标来选定聚类中心，避免了人为选取聚类中心可能出现的问题。另外，为了解决DPC 算法时间复杂度高的问题，本文在计算KNN 局部密度的过程中，采用KD-Tree 索引数据结构来帮助计算各数据对象的k 近邻，降低算法的时间复杂度，并且在计算相对距离的时候，只考虑数据对象的k 近邻，避免在计算相对距离时进行全局搜索。

定义5KNN 相对距离ωi。ωi是指数据对象xi与k 近邻内其他KNN 局部密度比它大的数据对象中的最短距离。其计算式如下

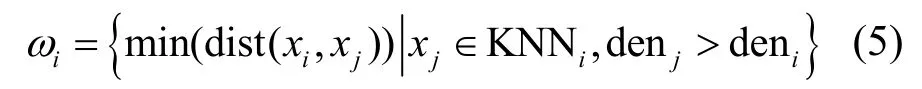
当数据对象xi是KNNi内的局部密度最大值时，将其放入邻居密度最大值集合maxden 中，然后将xi与maxden 中其他数据对象之间距离的最小值作为xi的KNN 相对距离ωi，即

定义6聚类中心决策指标ceni。ceni指数据对象xi的KNN 局部密度和KNN 相对距离的乘积。其计算式如下

得到KNN 局部密度deni、KNN 相对距离ωi以及聚类中心决策指标ceni后，根据用户初始化输入的聚类参数c选择ceni最大的前c个数据对象作为聚类中心。最后将数据集中剩余的数据对象依次分配到距离其距离最近的聚类中心完成聚类。快速密度峰值聚类（FDPC,fast density peak clustering）算法如算法2 所示。

算法2FDPC 算法

输入初始数据集D、参数k以及聚类数目c

输出c个聚类

1) 根据数据集D构建KD-Tree

2) for eachx∈Ddo

3) 根据KD-Tree 和式(3)计算数据对象x的KNN 距离

4) end for

5) for eachx∈Ddo

6) 采用式(4)计算x的KNN 局部密度

7) end for

8) for eachx∈Ddo

9) 采用式(5)和式(6)计算x的KNN 相对距离

10) end for

11) for eachx∈Ddo

12) 采用式(7)计算x的聚类中心决策指标

13) end for

14) 将聚类中心决策指标cen 前c大的数据对象作为聚类中心

15) 将数据集中剩余的数据对象分配至距离其最近的聚类中心

16) 完成聚类并输出c个聚类

2.2 FDPC-OF 算法描述

本文结合快速密度峰值聚类的度量指标提出FDPC-OF 算法。在完成聚类算法后，为了更好地刻画离群点在一些具有不同密度的数据集上的离群程度，将进一步对快速密度峰值聚类中的KNN 相对距离进行改进。

定义7平均向心距离davgi。davgi指聚类Ci中所有数据对象与聚类中心的平均距离。其计算式如下

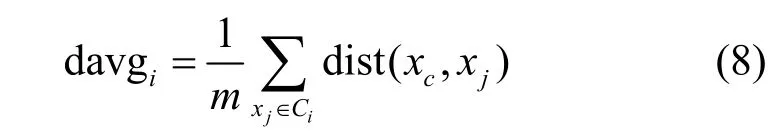
其中，m表示聚类Ci的数据对象个数；dist(xc,xj)表示数据对象xj和其所属聚类的聚类中心xc之间的距离。

定义8向心相对距离disceni。disceni指数据对象xi的KNN 相对距离ωi和其所属聚类的平均向心距离davgi的比值。其计算式如下

向心相对距离很好地刻画了离群点在一些不同密度的数据集上的离群程度。FDPC 二维数据分布如图3 所示。从图3 可以看出，24 号数据对象为全局离群点，其相对距离为最大值；25 号数据对象为局部离群点，其相对距离比稀疏聚类中的正常数据对象小，若把KNN 相对距离作为离群指标，局部离群点容易被稀疏区域的正常数据对象淹没。因此，本文在KNN 相对距离的基础上提出了平均向心距离。由于25 号数据对象属于左侧聚类，KNN相对距离与左侧聚类的平均向心距离的比值放大了该局部离群点的离群特征，更好地刻画了离群点的离群程度。

图3 FDPC 二维数据分布

定义9快速密度峰值聚类离群因子FOFi。FOFi指数据对象xi的向心相对距离disceni和KNN局部密度deni的比值。其计算式如下

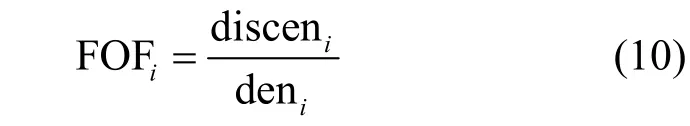
从密度上看，本文首先根据数据集构建KD-Tree，然后根据该索引结构计算数据对象的KNN 局部密度。该局部密度能很好地表示数据对象所处区域的密集程度。一般来说，离群点通常处于局部密度较低的区域。从距离上看，向心相对距离利用了聚类中心与数据对象之间的关系，能在一些具有不同密度的数据集上有较好的适应性，通常离群点的向心相对距离会比正常点大得多。因此，快速密度峰值聚类离群因子能很好地刻画数据对象的离群程度，通常情况下离群因子较大的点更有可能为离群点，因此算法选取排序后的离群因子中前o个点作为离群点输出，在算法实际应用中，o的取值是根据实际数据集的情况人为设定的。在本文实验中，为了验证所提FDPC-OF 算法在不同数据集上的有效性，o的取值根据数据集已有的离群点标签个数设定。FDPC-OF 算法如算法3 所示。

算法3FDPC-OF 算法

输入初始数据集D、参数k以及聚类数目c

输出o个离群点

1) 调用算法2 对数据集D进行聚类，输出c个聚类

2) for eachc∈Cdo

3) 采用式(8)计算c的平均向心距离

4) end for

5) for eachx∈Ddo

6) 采用式(9)计算x的向心相对距离

7) end for

8) for eachx∈Ddo

9) 采用式(10)计算x的快速密度峰值聚类的离群因子

10) end for

11) 降序排列快速密度峰值聚类的离群因子

12) 输出前o个点作为离群点

2.3 FDPC-OF 算法正确性

FDPC-OF 算法中，KD-Tree 索引数据结构能有效降低算法时间复杂度，从而提高算法的计算速率，基于KNN 对每个数据对象进行密度估计能很好地表示数据对象所处区域的疏密程度。根据算法2进行聚类，对每个聚类计算平均向心距离，将KNN相对距离与平均向心距离的比值作为向心相对距离能更好地在一些具有不同密度分布的数据集上放大离群点的离群特征。通过计算快速密度峰值聚类离群因子来刻画数据对象的离群程度，并对其进行降序排列，输出前o个离群点。

2.4 FDPC-OF 算法复杂性

FDPC-OF 算法的时间复杂度主要由以下2 个部分组成。1) 为计算数据对象的KNN 局部密度构建KD-Tree，时间复杂度为O(nlogn)，其中n为数据集的数据对象的个数。2) 计算数据对象的快速密度峰值聚类离群因子FOF(x)，时间复杂度为O(n) 。因此，FDPC-OF 算法总的时间复杂度为O(nlogn)+O(n) ≈O(nlogn)。

3 实验与分析

为了评估本文所提FDPC-OF 算法的性能，本节将在真实数据集和人工数据集上进行实验，并选取了几种不同的离群点检测算法进行对比实验，包括COF（connectivity-based outlier factor）算法[26]、NOF（natural outlier factor）算法[21]、RDOS（relative density-based outlier score）算法[27]、LDF（local density factor）算法[28]、IForest（isolation forest）算法[29]、NANOD（natural neighbour-based outlier detection）算法[30]和MOD（mean-shift outlier detector）算法[31]。实验环境如表1 所示。

表1 实验环境

3.1 实验评价指标

本文针对算法有效性的实验将选取3种性能评估指标，分别为：精确率Pr，计算方法如式(11)所示；加权评价指标F1 值，计算方法如式(13)所示；运行时间。其中，精确率也被称为查准率，F1 值结合了精确率和召回率Re 的表现。以上Pr 和F1 值的取值为0～1，其值越大表示离群点检测算法的检测效果越好。

其中，TP 为真阳性，表示算法正确检测为离群点的个数；FP 为假阳性，表示算法错误检测为离群点的个数；FN 为假阴性，表示算法将离群点检测为正常点的个数。

FDPC-OF 算法的相关参数设置如下：k 近邻中设置k=5，自动选取聚类中心时，设置聚类数量参数c=2。

对比算法的相关参数设置如下：RDOS 算法和COF 算法中，k=5；LDF 算法中，θ=0.5，k=5；NOF 算法和NANOD 算法为无参算法；IForest 算法和MOD 算法均采用原文献中的默认设置。

3.2 人工数据集

为了验证本文算法在各种不同的数据分布下离群点的检测能力，本文使用图4 所示的二维人工数据集D1～D4进行对比实验，其中，○表示离群点。D1～D4的数据特征如表2 所示。

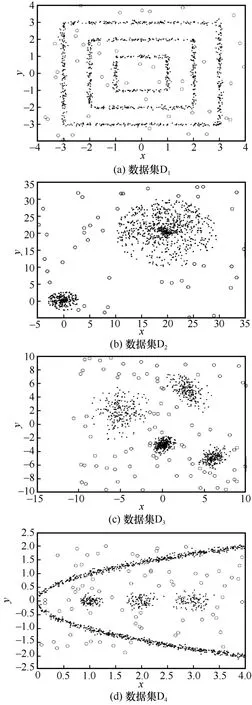
图4 二维人工数据集

表2 D1～D4 的数据特征

FDPC-OF 算法与对比算法在人工数据集上的精确率如表3 所示。从表3 可以看出，FDPC-OF算法在4 种人工数据集上的Pr 均值在95%以上，显著优于对比算法，在数据集D1上的Pr 高达100%；在数据集D2上的Pr 与LDF 算法相等，均在97%以上。FDPC-OF 算法在4 种人工数据集上的离群点检测稳定性优于对比算法，这是由于FDPC-OF 算法结合聚类中心的概念提出了向心相对距离，提高了算法在不同密度的数据集上的适用性。

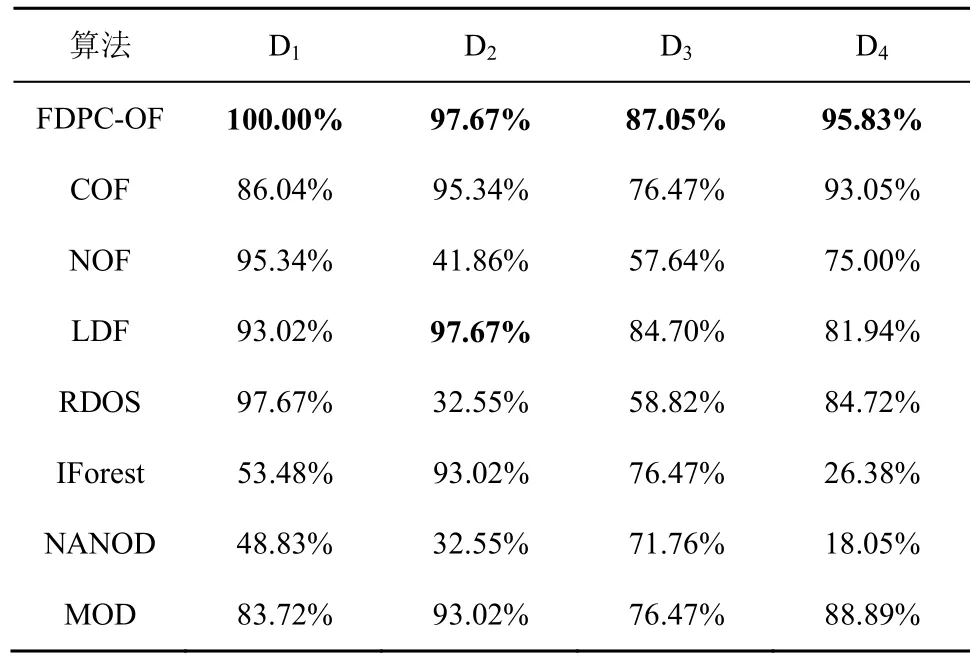
表3 不同算法在人工数据集上的精确率

FDPC-OF 算法与对比算法在人工数据集上的F1 值如表4 所示。从表4 可以看出，FDPC-OF 算法在4 个人工数据集上的F1 值的均值在93.5%以上，高于对比算法。LDF 算法在数据集D2上的F1值与FDPC-OF 算法相等，均在95%以上；RDOS算法的在数据集D1和D4上的F1 值表现较好，在D1上F1 值高达96.6%，但在数据集D2和D3上表现不佳；NANOD 算法在4 个人工数据集上整体表现不理想；MOD 算法在4 个人工数据集上表现稳定。从总体上看，FDPC-OF 算法的F1 值优于对比算法，在不同人工数据集上有着稳定的离群点检测效率，因此可以证明本文算法在人工数据集上的有效性。

表4 不同算法在人工数据集上的F1 值

FDPC-OF 算法与对比算法在人工数据集上的运行时间如图5 所示。从图5 可以看出，FDPC-OF算法在4 种人工数据集上的运行时间的均值仅为0.29 s，快于对比算法。IForest 算法由于不需要计算各数据对象之间的距离，因此时间复杂度为线性，在人工数据集上运行时间略长于FDPC-OF 算法；COF 算法、NOF 算法、RDOS 算法以及LDF算法需要计算各数据对象之间的距离，因此时间复杂度至少为O(n2)，与FPDC-OF 算法和IForest 算法有较大差距；MOD 算法在寻找KNN 邻域质心的过程中需要迭代计算，当数据量和维度增加时，该算法的时间复杂度会极大增加。FDPC-OF 算法在人工数据集上的运行时间在整体上优于对比算法，这是由于FDPC-OF 算法在计算k 近邻时使用了索引结构，从而降低了算法的时间复杂度，同时FDPC-OF算法计算过程简单。

图5 不同算法在人工数据集上的运行时间

3.3 真实数据集

本节采用4 种来自UCI的真实数据集[32]进行实验，分别是Ionosphere、Iris、Wdbc 和Vowels。真实数据集选取的离群点比例为3.4%～35.9%，属性个数为4～34 个，保证了离群点比例以及数据集的属性个数的多样性和复杂性，能更好地检验本文算法以及对比算法在真实数据集上的离群点检测能力。真实数据集的数据特征如表5 所示。

表5 真实数据集的数据特征

FDPC-OF 算法与对比算法在真实数据集上的精确率如表6 所示。从表6 可以看出，FDPC-OF算法在4 种真实数据集上的Pr 均值约为80%，高于对比算法。在Iris 数据集上，NANOD 算法表现最好，Pr 达到80%；在Wdbc 数据集上，FDPC-OF算法的Pr 与NANOD 算法和MOD 算法相等，为最高值。FDPC-OF 算法在不同规模、不同属性个数以及不同离群点比例的真实数据集上有着稳定的离群点检测效率。

表6 不同算法在真实数据集上的精确率

FDPC-OF 算法与对比算法在真实数据集上的F1 值如表7 所示。从表7 可以看出，FDPC-OF 算法在4 种人工数据集上的F1 值的均值在78.6%以上，高于对比算法。LDF 算法在Ionosphere 以及Iris数据集上的F1 值表现优异，均值在75%以上，但在其余数据集上表现一般；NANOD 算法和MOD算法的F1 值接近，在4 个真实数据集上都有着不错的表现，NANOD 算法在Iris 数据集上的F1 值表现最优，达到80%，MOD 算法在Wdbc 数据集上的表现与FDPC-OF 算法相等，为最高值。从总体上看，FDPC-OF 算法在F1 值的指标评估中有着不错的表现，结合精确度指标，本文提出的FDPC-OF算法在不同的真实数据集上有着稳定的离群点检测效率，因此可以证明本文FDPC-OF 算法在真实数据集上能稳定高效地检测出离群点。

表7 不同算法在真实数据集上的F1 值

FDPC-OF 算法与对比算法在真实数据集上的运行时间如图6 所示。从图6 可以看出，FDPC-OF算法在4 种人工数据集上的运行时间的均值仅为0.16 s，快于其他对比算法。在Ionosphere 以及Wdbc数据集上，FDPC-OF 算法、COF 算法以及IForest算法有着优异的运行速率，运行时间均少于1 s；在Iris 数据集上，各数据集的运行速率均有着不错的运行速率，运行时间均少于1 s；而在Vowels 数据集上除了本文FDPC-OF 算法以及IForest 算法的运行时间少于1 s 以外，其他算法的运行速率表现不佳，其中NOF 算法、RDOS 算法以及LDF 算法的运行时间超过40 s。本文算法在处理大规模数据集时，仍然有着十分优异的运行速率，在真实数据集上的运行速率在整体上快于其他对比算法，因此本文算法的计算效率优异。

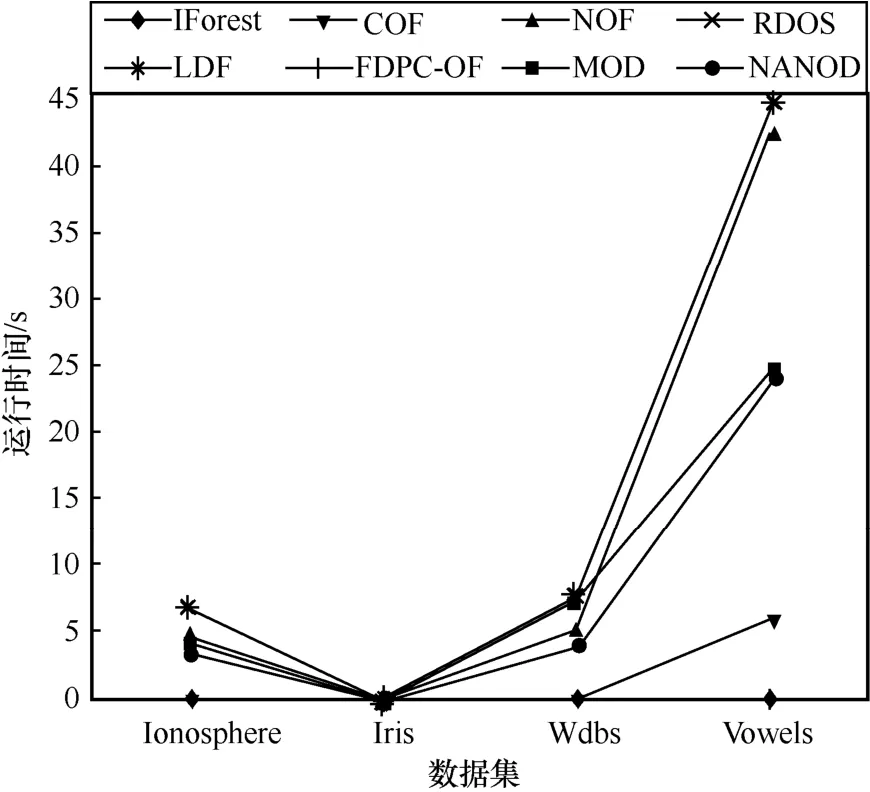
图6 不同算法在真实数据集上的运行时间

4 结束语

本文首先分析了密度峰值聚类DPC 算法和其算法思想，针对密度峰值聚类算法时间复杂度高以及需要人工设置参数的问题进行了深入的研究，给出了一种快速密度峰值聚类算法，使用k 近邻算法代替密度峰值聚类中的密度估计，使用索引数据结构对距离计算进行优化，极大地减少了聚类的时间复杂度，并避免了设置截断距离dc。本文定义了向心相对距离，给出了基于快速密度峰值聚类离群因子来刻画数据对象的离群程度，从而提出了基于快速密度峰值聚类离群因子的离群点检测算法。对所提算法的正确性和复杂性进行分析，在人工数据集和真实数据集上的实验证明，FDPC-OF 算法能够高效全面地检测出离群点。