基于带智能卡的移动终端实现的隐私保护的属性票据方案
史瑞,封化民,谢惠琴,史国振,刘飚,杨旸
(1.北京邮电大学网络空间安全学院,北京 100876;2.北京电子科技学院,北京 100070;3.福州大学数学与计算机科学学院,福建 福州 350108)
0 引言
电子票据是用户属性信息、纸质票据和实体证件的电子化版本。随着智能移动终端(如智能手机、平板电脑)的普及和高速互联网络(如5G、Wi-Fi)的应用,电子票据正逐步取代纸质票据和实体卡成为人们日常生活的必需品。例如,我国已经广泛使用电子医保卡代替实体医保卡就医,人们可在移动端完成挂号、取号和缴费等流程。在一些国家,航空、地铁和出入境票据的管理已全面电子化,人们可在手机上自助完成买票、检票和退票流程。此外,在购物、住宿、娱乐等领域,会员卡、年卡、优惠券和电影票等各种票据也已逐步电子化。
虽然关于电子票据的研究已有许多成果[1-17],但是在移动应用场景中部署电子票据系统仍然面临着一些至今没有解决的问题。1) 无法将电子票据系统部署在资源受限的设备中(如智能卡)。智能卡设备由于功耗低、存储安全和携带方便等优点成为部署电子票据的最合适的平台。已有的属性票据方案[6,17]虽然可以在功能强大的设备(如个人计算机)中使用,但是这些方案使用了耗时的双线性映射运算,而目前标准的智能卡设备不支持这类运算,因此它们无法在轻量级设备中部署。2) 无法防止电子票据在未授权设备(用户)之间共享。在交通、购物、娱乐等商业领域中部署电子票据系统所带来的一个重要问题是无法阻止未付费(未授权)设备(用户)访问服务。解决这个问题的最直接方法是将票据的秘密信息存储在安全硬件设备中(如具有安全存储和防复制功能的智能卡),使没有安全硬件的参与就无法完成票据购买和消费协议。这不仅可以解决恶意用户不受限制地共享票据的问题,而且为诚实用户增加了额外的安全防护。
智能卡设备虽然有很多优点,但是其没有完整的电源和通信装置,因此需要借助外部辅助设备,通过接触或非接触方式才能完成读写和运算操作。因此,不依赖辅助设备而单独在智能卡上实现用户端的电子票据协议是不可能的。移动终端(如智能手机)由于部署面广、使用频率高、外部接口丰富、计算和通信效率高等优点是目前作为辅助设备的最优选择。这种以智能卡作为核心设备,移动终端作为辅助设备的模式已得到广泛应用。例如,在与银行的认证协议中,用户的硬件部分由U 盾(智能卡)和智能手机(移动终端)组成,其中,U 盾是可信的并负责存储用户私钥和执行数字签名,智能手机负责执行账号管理和网络通信;银行在线转账的安全性由U 盾保障而不依赖于智能手机,即使智能手机是恶意的也无法通过获取U 盾中用户私钥的方式伪造转账。为了解决电子票据系统面临的上述问题,本文提出了一个基于带智能卡的移动终端(如带U 盾的智能手机)部署的属性票据方案。
在本文的系统架构中,用户的硬件部分由一张资源受限但安全可信的智能卡和一部功能强大的移动终端组成。其核心思想是将智能卡作为用户的核心设备,存储用户的所有秘密信息,并执行与密钥有关但轻量化的运算;将移动终端作为用户的辅助设备,执行与密钥无关但耗时的运算;每个用户的智能卡唯一,而移动终端可以随时替换,且没有智能卡的参与移动终端无法完成任何协议。
本文给出了基于带智能卡的移动终端实现的属性票据方案的系统模型和安全模型,并结合伪随机函数、匿名的临时身份方案、带随机化标签的可聚合签名和Pointcheval-Sanders(PS)签名提出了一个高效的构造实例,证明了所提方案满足不可伪造性和不可链接性的安全需求。
在所提方案的用户运算中,除了用户的注册验证和票据验证操作需要移动终端参与外,剩余的用户注册请求、票据购买请求和票据消费请求都可由智能卡单独完成,且移动终端参与的操作不需要任何用户秘密信息的参与。此外,用户的私钥和票据秘密信息不出卡,用户的身份、公钥、属性和证书等公开信息也可存储在智能卡中。因此,即使移动终端是恶意的,也无法在没有智能卡的参与下完成电子票据的任何协议。
所提方案支持基于属性泄露的购票策略,可在最小化信息泄露的原则下完成票据购买,最大程度地保护了用户隐私。例如,学生购买优惠票据时只需泄露“学生”属性,而学号、学院、住址、电话等敏感信息都应保密。与最新的属性票据方案[6,17]使用耗时的零知识证明和基于属性的随机化签名实现支持属性泄露策略的票据购买协议不同,所提方案使用一种聚合的方法构造用户属性证书,显著降低了票据购买算法的计算复杂度。
在票据购买协议中,智能卡发送完票据购买请求后,可能由于意外或恶意的行为导致其在没有收到卖方返回的票据验证信息的情况下被强制断电,如智能卡从移动终端上被突然拔出或移动终端突然掉电。在这种情况下,即使智能卡重新上电,由于不能实时保存协议执行的上下文信息,将会导致用户购票失败。为了解决这个问题,在所提方案中使用带密钥的伪随机函数产生票据购买请求和卖方票据验证都需要的上下文信息。这意味着用户可以在智能卡上电后重新恢复上下文再验证票据的正确性。
通过与最新的属性票据方案[6,17]在个人计算机(华为Matebook)上的实验对比,所提方案实现了最优的效率。通过在国产智能卡(爱信诺ACH512)和智能手机(华为荣耀9i)上的实验显示,所提方案完成一次票据购买算法需要在智能卡上消耗约369 ms,在移动终端上消耗约196 ms;完成一次票据消费算法只需要在智能卡上消耗约197 ms。
Mut-Puigserver 等[1]按照功能需求(有效期、灵活性等)和安全需求(不可链接性、不可伪造性、传递性、不可双花等)将电子票据方案分为可传递票据[2-3]、不可传递票据[4]、一次性票据[2-5]和可多次使用的票据[1,4]。此外,Han 等[6]还提出了支持属性策略的电子票据。本文的研究内容是不可传递、一次性和支持属性策略的电子票据方案。
Fan 等[7]、Song 等[8]、Quercia 等[9]、Rupp 等[10],以及Milutinovice 等[4]分别利用不同的盲签名[11]提出了保护用户隐私的电子票据方案,但是他们的方案都不支持票据的不可传递性。Nakanishi 等[12]和Vives-Guasch 等[13]分别使用不同的群签名[14]提出了电子票据方案,虽然他们的方案支持不可链接性和不可传递性,但是不支持属性策略。Heydt-Benjamin 等[3]和Arfaoui 等[15]分别利用匿名证书[16]提出了电子票据方案,但是他们的方案不支持属性策略,也没有正式的安全证明。Han 等[6]使用随机化签名和零知识证明提出了首个支持属性策略的电子票据方案,但是该方案使用了大量的双线性对运算实现票据购买和票据消费算法,因此无法应用在智能卡设备中使用。封化民等[17]使用结构保持签名和可延展签名等提出了一个可转让的强隐私保护的属性票据方案,该方案首次在票据验证协议中同时实现了用户和卖方的匿名性,但是票据购买算法仍然需要4 个双线性映射运算,因此无法在智能卡设备中部署。
Mostowski 等[18]在智能卡上实现了U-prove 匿名证书方案;Camenisch 等[19]提出了一个适用于智能卡实现的带密钥验证的匿名证书方案;Verheul等[20]提出了一个在智能卡上实现的可自盲化的匿名证书方案。这些不同类型的证书方案虽然可在智能卡上部署,但是它们都不是属性票据方案。Hanzlik 等[21]提出了一种在核心辅助环境下部署的匿名证书方案,该方案中用户由核心设备(如智能卡)和辅助设备(如智能手机组成)组成,为在移动环境下部署匿名证书提供了一种新的方法。
1 预备知识
1.1 双线性对
设 G1,G2,GT是阶为素数p的循环群,g和分别是 G1和G2的生成元。TYPE-3 型双线性[22]映射e:G1×G2→GT满足双线性、非退化性和可计算性,且 G1和G2之间不存在同态映射。
1.2 零知识的知识签名
对于任意的多项式时间非确定性(NP,non-deterministic polynomial)关系R,NP 语言LR={y: ∃x,(x,y)∈R}的零知识的知识签名(ZKSoK,zero knowledge signature of knowledge)[23]定义为。如果知识签名满足正确性、可模拟性和可提取性,则知识签名是模拟提取安全的。
1.3 平方离散对数假设
设G 是阶为素数p的循环群,g'是G 的生成元。平方离散对数(SDL,square discrete logarithm)假设是指给定三元组,其 中,任意概率多项式时间(PPT,probabilistic polynomial time)敌手求解x的概率是可忽略的。
1.4 判定性平方Diffie-Hellman 假设
设G 是阶为素数p的循环群,g'是G 的生成元。判定性平方Diffie-Hellman(DSqDH,decisional square diffie-hellman)假设[24]是指给定三元组其中,任意PPT 敌手区分出下面2 种情形的概率是可忽略的:y=x2;y从中随机选取。
1.5 伪随机函数
伪随机函数(PRF,pseudorandom function)由密钥生成和伪随机数生成2 个算法组成。
1) 密钥生成:PRF.KeyGen(1λ) → psk,产生一个密钥。
2) 伪随机数生成:对于一个有限的集合S 和任意字符串x∈ {0,1}*,输出随机数y=PRF.Evalpsk(x),其中y∈S。
1.6 匿名的临时身份
匿名的临时身份(AET,anonymous ephemeral tag)方案[24]由初始化、标签生成、标签随机化、标签证明和标签验证算法组成。
1.7 带随机化标签的可聚合签名
带随机化标签的可聚合签名(ASRT,aggregatable signature with randomizable tag)[24]由初始化、密钥生成、签名、聚合并随机化签名和验签算法组成。在一般群模型下[25],如果对每一个标签-索引对签名预言机只能被询问一次,那么带随机化标签的可聚合签名是不可伪造的。如果DSqDH 问题是难解的,那么带随机化标签的可聚合签名是不可链接的。
1.8 Pointcheval-Sanders 签名
支持隐藏消息签发的PS(Pointcheval-Sanders)签名[26]由初始化、密钥生成、签名协议和验签算法组成。在一般群模型下,PS 签名[26]在选择消息攻击模型下是不可伪造的。
2 系统模型和安全模型
2.1 系统架构
系统架构如图1 所示。基于带智能卡的移动终端实现的隐私保护的属性票据方案由4 类实体组成:证书中心(CA)、卖方(S)、用户(U)和验证方(V),用户的硬件部分由一张智能卡(如U 盾)和一部移动终端设备(如智能手机)组成。智能卡存储用户的所有密钥信息并执行与密钥相关的运算,移动终端执行与密钥无关但耗时的运算。智能卡是安全可信的,敌手无法复制智能卡或从智能卡导出用户的秘密信息。移动终端是诚实但好奇的,一方面它诚实地与智能卡协作完成电子票据协议;另一方面它好奇用户的密钥和票据秘密信息。验证方维护一个只能添加的公开数据库用于存储已消费票据的标识。
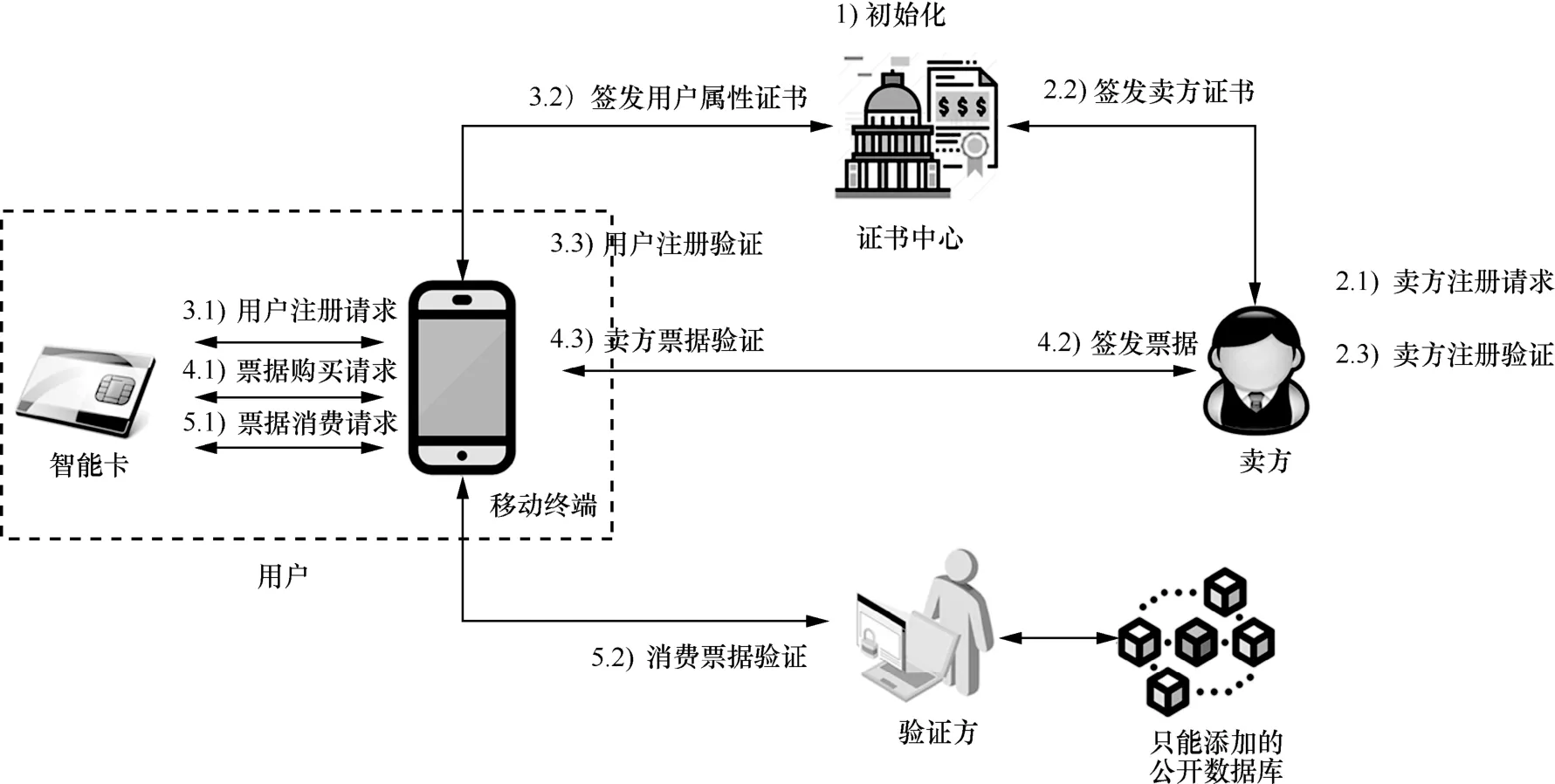
图1 系统架构
方案的工作流程如下所述。
步骤1系统初始化。CA 执行系统初始化操作,产生系统公共参数、主公私钥对和一个票据策略集合。其中,系统公共参数、主公钥和票据策略集合公开,使其他参与实体可以获得。
步骤2卖方注册。2.1) S 产生卖方公私钥对,并向CA 发起卖方注册请求;2.2) CA 验证S 的请求后为S 签发卖方证书;2.3) S 验证CA 返回的卖方证书后将其保存在本地。
步骤3用户注册。3.1) U 的智能卡设备生成用户公私钥对(私钥不出卡),并通过移动终端设备的信道向CA 发起注册请求;3.2) CA 验证U 的注册请求后为U 签发用户属性证书;3.3) U 的移动终端设备收到CA 返回的用户证书后与智能卡设备协作验证其正确性后将其保存在本地。
步骤4票据购买和发布。4.1) 为了向S 证明U 已被CA 认证且其泄露的属性集合符合票据策略集合中的一条属性策略,U 的智能卡设备计算一个属性泄露证明,并通过移动终端设备的信道向S 发起票据购买请求;4.2) S 验证U 的购买请求后为U 签发票据;4.3) U 的移动终端设备收到票据并与智能卡设备协作验证其正确性后将其保存在本地。
步骤5票据消费和验证。5.1) U 的智能卡设备产生票据消费证明并通过移动终端设备向V 发送票据消费请求;5.2) V 收到消费请求后,首先检查票据是否双重消费,然后验证其合法性。
2.2 威胁模型
CA 是诚实可信的。它诚实地产生安全的系统参数、主公私钥对和一个票据策略集合;它诚实地验证卖方和用户的身份和属性信息,并为合法卖方和用户签发证书。
S 是诚实且好奇的。它诚实地验证用户的合法性以及用户泄露的属性子集与票据策略的一致性;它诚实地为合法用户签发票据,但好奇用户的真实身份和隐藏的属性信息。
U 是恶意的。恶意的用户通过伪造用户的证书购买合法票据,或者直接伪造一个票据试图通过V的验证,或者双重消费一个合法票据。
V 是诚实且好奇的。它诚实地维护公开数据库,检查票据消费请求是否是双重消费,验证票据消费请求是否合法,但好奇用户的真实身份信息。
2.3 形式化定义
安全的智能卡设备具有防复制和安全存储功能,可以有效地阻止移动终端读取用户密钥的行为,从硬件层面确保了好奇的移动终端无法获得智能卡中的密钥,也就不会影响用户侧的安全性,因此在本节中将用户的智能卡和移动终端设备统称为用户而不再加以区分。表1 给出了所提方案常用的符号定义。隐私保护的属性票据方案由5 个算法组成。

表1 符号定义
1) 系统初始化算法:Setup(1λ,n) → (pp,P,msk,mpk)。此算法由CA 执行。CA 输入一个安全参数1λ和一个正整数n,输出系统参数pp、主私钥msk 和主公钥mpk。
2) 卖方注册算法:SReg(S(pp) ↔CA(pp,msk,mpk)) →((ssk,spk,creds)/ ⊥)。此算法由S 和CA 交互执行。S 输入pp,CA 输入pp、msk和mpk。若算法执行成功,S 输出卖方私钥ssk、卖方公钥spk和卖方证书 creds,否则算法输出⊥。
2.4 安全性定义
为了在防止恶意用户伪造票据的同时保护诚实用户的隐私,属性票据方案应该同时满足不可伪造性和不可链接性。所提方案的安全性定义遵循文献[6,17]的工作,不同之处是为了使安全性的定义更准确地反映威胁模型,本文将不可伪造性分为证书的不可伪造性和票据的不可伪造性,将不可链接性分为证书的不可链接性和票据的不可链接性。
首先,给出安全性定义需要调用的全局变量和预言机。定义A 为PPT 敌手,C 为挑战者。在实验中,C 向A 模拟所有预言机,所有预言机都可以访问全局变量。
全局变量介绍如下。
1) HU:存储诚实用户身份的列表。
2) CU:存储恶意用户身份的列表。
3) HS:存储诚实卖方身份的列表。
4) CS:存储恶意卖方身份的列表。
5) SR:存储卖方私钥、公钥和证书的列表。
6) UR:存储用户身份、私钥、公钥、属性和证书的列表;
7) TKT:存储用户身份、卖方身份、票据、票据有效期和票据唯一标识的列表。
8) TOK:存储用户身份、卖方身份、票据和票据消费请求的列表。
预言机介绍如下。

3) OCU(i):此预言机用于描述A 获得一个诚实用户i的秘密信息。如果i∉HU,则返回⊥;否则,查询UR[i],从HU 删除i,添加CU←i,返回
4) OSReg(j):此预言机用于描述一个诚实卖方j和CA 执行卖方注册算法。如果j∈ HS ∪ CS,则返回⊥;否则,CA 和j执行算法SReg(S(pp)↔CA(pp,msk,mpk) →((ssk,spk,creds)/ ⊥)。如果算法输出⊥,则返回⊥;否则,设置HS←j,SR[j] ← (j,ssk,spk,creds)。
5) OSReg.CA(j):此预言机用于描述一个恶意卖方j和CA 执行卖方注册算法。如果j∈ HS ∪ CS,则返回⊥;否则,CA 和A 执行算法:SReg(A(·) ↔CA(pp,msk,mpk) →((ssk,spk,creds)/ ⊥),其中卖方j的运算部分由A 执行。如果算法输出⊥,则返回⊥;否则,设置HS←j,SR[j] ← (j,*,spk,creds),其中*为未知私钥。
6) OCS(j):此预言机用于描述A 获得一个诚实卖方j的秘密信息。如果j∉HS,则返回⊥;否则,查询SR[j],从HS 删除j,添加CS←j,返回(j,ssk,spk,creds)。
7) OObtIss(i,j,I):此预言机用于描述一个诚实用户i和一个诚实卖方j执行票据购买和发布算法。如果i∉ HU,j∉ HS,I⊄ [1,n],则返回⊥;否则,查询 UR[i]和 SR[j],并执行算法如果算法输出⊥,则返回⊥;否则,设置TKT[i][j]←(i,j,tkt,VP,sn)。
8) OObtain(i,j,I):此预言机用于描述一个诚实用户i和一个恶意卖方j执行票据购买和发布算法。如果i∉ HU,j∉ CS,I⊄ [1,n],则返回⊥;否则,查询 UR[i],并和 A 执行算法,其中卖方j的运算部分由A 执行。如果算法输出⊥,则返回⊥;否则,设置TKT[i][j] ←(i,j,tkt,VP,sn)。
9) OIssue(i,j,I):此预言机用于描述一个恶意用户i和一个诚实卖方j执行票据购买和发布算法。如果i∉ CU,j∉ HS,I⊄ [1,n],则返回⊥;否则,查询 SR[j],并和 A 执行算法。如果算法输出⊥,则返回⊥;否则,设置TKT[i][j] ←(i,j,*,VP,*),其中*为未知票据和未知票据标识。
10) OShow(i,j,k):此预言机用于描述一个诚实用户i和一个恶意验证方k执行票据消费和验证算法。如果i∉HU,则返回⊥;否则,查询UR[i]、SR[j]和TKT[i][j],并和 A 执行算法,其中验证方的计算部分由A 执行。如果算法输出0,则返回0;否则,设置TOK[i][j] ←(i,j,tkt,tok),并返回1。
证书的不可伪造性确保恶意的用户无法通过伪造证书从卖方购买票据。在证书不可伪造性实验中,敌手模拟恶意用户的行为且允许敌手询问CA和诚实卖方的预言机。如果在实验结束时,敌手在票据购买算法中输出了一个未注册用户或已注册诚实用户的合法购买请求,则敌手赢得了实验。
定义1证书的不可伪造性。在 EXPunf-cred(A,λ,n)中,如果对任意的PPT 敌手A,存在可忽略函数ε(λ),使,则属性票据方案满足证书的不可伪造性。

4) 如果b=⊥或i*∈CU或j*∉HS,返回0;
5) 返回1。
票据的不可伪造性确保了恶意用户无法通过伪造票据通过验证方的验证。在票据的不可伪造性实验中,敌手模拟恶意用户的行为且允许敌手询问CA 和诚实卖方的预言机。如果在实验结束时,敌手在票据消费算法中输出了一个未注册用户或已注册诚实用户的合法的票据消费请求,则敌手赢得了实验。
定义 2票据的不可伪造性。在 EXPunf-tkt(A,λ,n)中,如果对任意的PPT 敌手A,存在可忽略函数ε(λ),使则属性票据方案满足票据的不可伪造性。
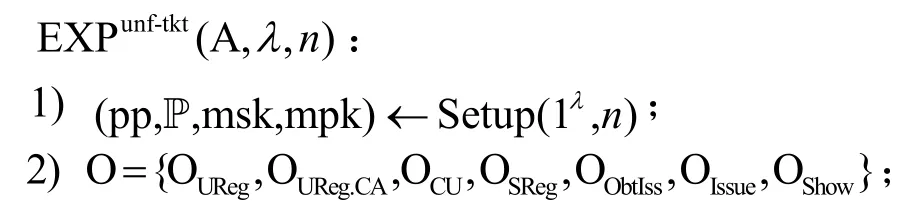
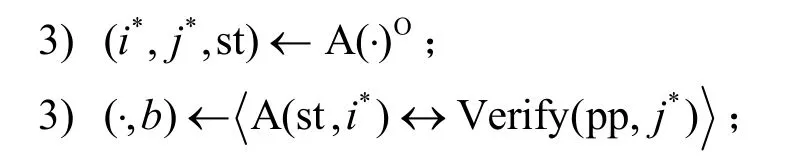
4) 如果b=0或i*∈CU或j*∉HS,返回0;
5) 返回1。
证书的不可链接性确保了好奇的卖方无法通过为用户签发票据获取用户的任何身份和隐藏的属性信息,具体指卖方无法将任意的2 个票据购买请求链接。
定义 3证书的不可链接性。在(A,λ,n)中,如果对任意的PPT 敌手A,存在可忽略函数ε(λ),使ε(λ),则属性票据方案满足证书的不可链接性。

4) 如果b*=b,返回1;
5) 返回0。
票据的不可链接性确保了好奇的验证方(也同时是卖方)无法通过验证票据消费请求获取用户的任何身份信息,具体指验证方无法将任意的2 个票据消费请求链接。
定义 4票据的不可链接性。在(A,λ,n)中,如果对任意的PPT 敌手A,存在可忽略函数ε(λ),使ε(λ),则属性票据方案满足票据的不可链接性。

5) 如果b*=b,返回1;
6) 返回0。
3 方案设计
3.1 设计思想
构造电子票据方案面临的主要挑战是在满足上文定义的系统模型和安全模型下将用户的所有运算轻量化,使其可在智能卡上高效实现。
为了在票据购买算法中实现高效的属性泄露证明,所提方案将匿名的临时身份作为用户公钥,使用户公钥成为一个可随机化的标签;在用户注册时,CA 对每个用户属性分别签发一个带随机化标签(用户公钥)的签名;在购买票据时,用户只需按照票据策略将需泄露的属性对应的多个签名聚合,然后将用户公钥和聚合后的签名随机化后发送给卖方。这种方法避免了将大量不需要泄露的属性隐藏在签名中,且聚合签名和用户公钥的随机化操作只需 G1上的幂运算,提高了票据购买的效率。
为了阻止双花消费,在票据购买时为每个票据产生唯一的标识;当消费票据时,验证方可根据票据唯一标识检查票据是否为双重消费。在票据购买和发布算法中,票据的唯一标识不能泄露给卖方(如果泄露将破坏票据的不可链接性),因此票据发布算法需支持隐私属性的票据签发。为此,所提方案使用支持高效协议的PS 签名构造用户票据。在票据购买时,用户产生一个票据标识的承诺;在票据发布时,卖方在承诺上签名;在票据消费时,所提方案使用了文献[27]的方法,避免了用户执行耗时的双线性映射运算。此外,为了防止智能卡突然断电导致的购票失败,所提方案利用带密钥的伪随机函数生成票据购买算法的上下文信息,使智能卡重新上电后仍可验证卖方返回的票据。
3.2 方案构造


2) 卖方注册:SReg(S(pp) ↔CA(pp,msk,mpk)) →((ssk,spk,creds)/ ⊥)。
如图2 所示,为了获得卖方证书,首先,S 产生PS 签名私钥ssk 和公钥spk;然后,S 计算知识签名π1证明其拥有ssk 的知识;最后将注册请求信息 (spk,π1)发送CA。CA 验证S 的身份和π1后,计算PS 签名 creds,并返回S。S 验证 creds的正确性后,将 creds作为证书保存。

图2 卖方注册算法
如图3 所示,为了获得卖方证书,首先,智能卡产生伪随机函数的密钥ρ和私钥μ,并设置用户密钥usk=(ρ,μ);然后,智能卡计算与用户身份id绑定的随机元素h,并计算公钥upk;最后,智能卡计算知识签名π2证明其拥有μ的知识,并将注册请求发送给移动终端。移动终端收到智能卡的注册请求后转发给CA。CA 验证U的身份、属性信息和π2后,分别为每个属性-标签对(mi,upk)计算ASRT 签名σi,并将返回U。移动终端验证 credu的正确性后,将其发送给智能卡。智能卡将 credu作为证书保存。

图3 用户注册算法
如图4 所示,为了获得票据,首先,智能卡从移动终端收到一个S 产生的挑战随机数nounce;然后,智能卡将需泄露的属性集合对应的签名{σi}i∈I聚合为一个签名σ,并将用户公钥和聚合签名随机化为(upk',σ');为了防止双重消费,智能卡使用伪随机函数生成票据唯一标识sn 和加密密钥t,并使用ElGamal[28]算法将μ和sn 的承诺加密为T;最后,智能卡计算知识签名π3证明其拥有秘密信息 (μ,t,sn),并将票据购买请求(upk',σ',T,{mi}i∈I,π3)发送给移动终端。移动终端收到智能卡的票据购买请求后转发给S。S 首先验证π3、upk'和σ'后,然后设置票据有效期VP,最后计算 PS 签名(α,β),并将票据验证信息(α,β,VP)返回用户。移动终端收到票据验证信息后将其转发给智能卡,智能卡使用密钥t解密后获得票据 (T1,T2);为了不泄露票据秘密信息的同时验证票据的正确性,智能卡计算T~,并将 (T1,T2,T)发送移动终端;移动终端验证通过后,智能卡设置票据 tkt=(T1,T2),并将(tkt,VP,sn)保存。

图4 票据购买和发布算法
如图4 所示,在票据购买算法中,用户使用临时产生的加密密钥t和票据唯一标识sn 参与计算票据购买请求,同时t和sn 作为协议的上下文信息也用于验证卖方签发的票据。如果用户发送完票据购买请求后设备意外断电,用户(智能卡)可使用伪随机函数重新恢复t和sn,从而继续完成票据验证而不需要重新发起购票请求。


如图5 所示,为了消费票据,首先,智能卡将票据tkt 随机化为tkt';然后,为了在泄露票据唯一标识sn 和票据有效期VP 的同时证明tkt'的正确性,智能卡计算κ和ν;最后,智能卡计算知识签名π4证明其拥有用户密钥的知识,并将票据消费请求tok=(tkt',κ,ν,π4,sn,VP)发送V。V 收到票据消费请求后,首先验证其有效期和是否为双重消费,然后验证π4和tkt'的正确性,若验证通过,V 输出1,否则输出0。
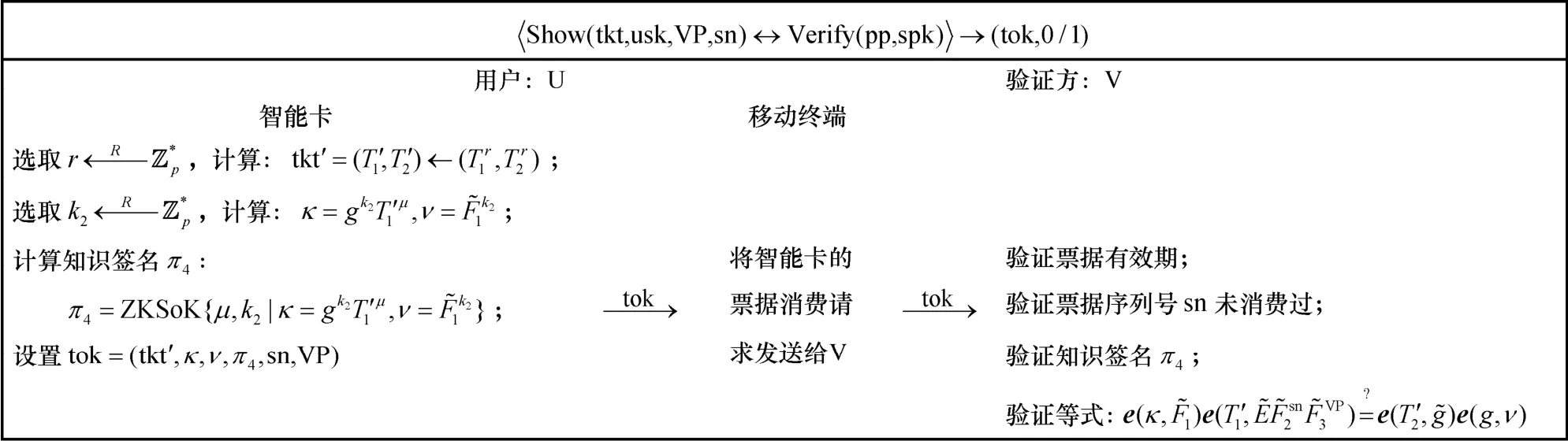
图5 票据消费和验证算法
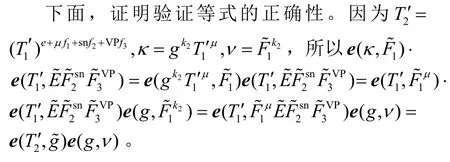
4 安全性分析
4.1 证书的不可伪造性
定理1如果SDL 问题在 G1上是难解的且ASRT 签名是不可伪造的,那么所提方案满足证书的不可伪造性。
证明如果敌手赢得了证书的不可伪造性实验 EXPunf-cred(A,λ,n),敌手或者伪造了一个未注册用户或者伪造了一个已注册诚实用户的票据购买请求。
引理1如果敌手A 在证书的不可伪造性实验中以不可忽略的概率ε(λ)伪造了一个诚实用户的购买请求,那么存在挑战者C 以的概率求解SDL 问题,其中q为诚实用户数量。
证明假设是一个SDL 挑战,C使 用(g,G1)作为参数,执行(pp,P,msk,mpk)←Setup(1λ,n)产生剩余参数,并将(pp,P,mpk)发送 A。C 猜测一个诚实用户i*∈HU,使得实验结束时,A 伪造了i*的一个票据购买请求。

2) OCU(i):如果i≠i*,C 的模拟与真实的执行一致;否则,返回⊥。

4) OUReg.CA,OSReg,OIssue:因为C 拥有CA 和S的密钥,所以可以完美地模拟这些预言机。
如果A在票据购买算法中伪造了诚实用户i*的票据购买请求(概率为因为知识签名π3是模拟提取安全的,那么C 可提取i*的密钥μ*,且成功的概率为。证毕。
引理2如果敌手A 在证书的不可伪造性实验中以不可忽略的概率ε(λ)伪造了一个未注册用户的购买请求,那么存在挑战者C 以相同的概率伪造ASRT 签名。

4.2 票据的不可伪造性
定理2如果SDL 问题在 G1上是难解的且PS签名是不可伪造的,那么所提方案满足票据的不可伪造性。
证明如果敌手赢得了票据的不可伪造性实验 EXPunf-tkt(A,λ,n),敌手或者伪造了一个未注册用户或者伪造了一个已注册诚实用户的票据消费请求。
引理3如果敌手A 在票据的不可伪造性实验中以不可忽略的概率ε(λ)伪造了一个诚实用户的购买请求,那么存在挑战者C 以的概率求解SDL 问题,其中q为诚实用户数量。
证明假设是一个SDL 挑战,C使用(g,G1)作为参数,执行(pp,P,msk,mpk)←Setup(1λ,n)产生剩余?参数,并将(pp,P,mpk)发送A。C 猜测一个诚实用户i*∈HU,使得实验结束时,A 伪造了i*的一个票据购买请求。
C 可向A 模拟如下预言机。
1) OUReg,OCU,OObtIss,OUReg.CA,OSReg,OIssue:C 的模拟与引理1 一致。
2) OShow(i,j,k):如果i≠i*,C 的模拟与真实的执行一致;否则,C 计算,并通过模拟知识签名π4完成票据消费。
如果A在票据消费算法中伪造了诚实用户i*的票据消费请求(概率为),因为知识签名π4是模拟提取安全的,那么C 可提取i*的密钥μ*,且成功的概率为。证毕。
引理4如果敌手A 在票据的不可伪造性实验中以不可忽略的概率ε(λ)伪造了一个未注册用户的消费请求,那么存在挑战者C 以的概率伪造PS 签名,其中q为诚实卖方的数量。
证明C 执行PS 签名的不可伪造性实验,获得公共参数pp 和签名公钥F2,F3),且C 可以不限次数的询问PS 签名预言机使用pp 作为参数,执行(pp,P,msk,mpk) ←Setup(1λ,n)产生剩余参数,并将(pp,P,mpk)发送A。
C 猜测A 将伪造卖方j*签发的票据,并向A模拟如下预言机。
1) OSReg(j):如果j≠j*,C 的模拟与真实的执行一致;否则,C 设置 spkj*=spkps,并通过模拟知识签名π1完成卖方注册。
2) OIssue(i,j,I):如果j≠j*,C 的模拟与真实的执行一致;否则,C 将(T,VP)发送,然后将输出的签名(α,β)和VP 都返回A。
3) OObtIss(i,j,I):如果j≠j*,C 的模拟与真实的执行一致;否则,C 随机选择,将(μi,sn,VP)发送,然后将输出的签名 (T1,T2)作为票据保存在全局变量。
4) OUReg,OUReg.CA,OCU,OShow:因为C 拥有用户、CA 的私钥和S 的公钥,因此可以完美地模拟这些预言机。

4.3 证书的不可链接性
定理3如果DsqDH 问题在 G1上是难解的,那么所提方案满足证书的不可链接性。
证明如果敌手以不可忽略的概率ε(λ)赢得证书的不可链接性实验,那么存在挑战者C 以的概率求解 G1上的DsqDH 问题,其中q为诚实用户数量。
在实验的第一阶段,C 向A 模拟如下预言机。

2) OObtIss,OObtain:C 的模拟与引理 1 中的OObtIss(i,j,I)一致。
3) OSReg,OSReg.CA,OCS:因为C 拥有CA 和S 的密钥,所以可以完美地模拟这些预言机。
在实验的某个阶段,A 输出2 个诚实用户身份i0,i1和一个卖方身份j。如果ib≠i*(概率为那么C 中止实验,否则继续模拟如下预言机。

如果η=μ2,C 的模拟是完美的;否则,(upk',σ',T)都是随机元素,此时A 无法以不可忽略的概率赢得实验。除非实验中止,A 的任何输出都可以被C 用于解决DsqDH 问题,因此C 成功的概率为。证毕。
4.4 票据的不可链接性
定理4如果DsqDH 问题在 G1上是难解的,那么所提方案满足票据的不可链接性。
证明如果敌手以不可忽略的概率ε(λ)赢得票据的不可链接性实验,那么存在挑战者C 以的概率求解 G1上的DsqDH 问题,其中q为诚实用户数量。
实验设置与第一阶段预言机的模拟与定理3 相同,除了下面的预言机。
1) OShow(i,j,k):如果i≠i*,C 的模拟与真实的执行一致;否则,C 计算,并通过模拟知识签名π4完成票据消费。
在实验的某个阶段,A 输出2 个诚实用户身份i0,i1和一个卖方身份j。如果ib≠i*(概率为),那么C 中止实验,否则继续模拟如下预言机。

5 效率分析
5.1 理论分析
表2 将所提方案与最新的电子票据方案在功能上进行了比较,其中√表示支持此项,×表示不支持此项。核心辅助设置指是否支持将用户的计算安全地分割为智能卡和移动终端实现;属性票据指是否支持属性泄露策略;不可转让指是否支持不可转让性;安全证明指是否有形式化的安全性证明;双花检测指是否能够检测双重消费;不可链接性和不可伪造性指是否支持此类安全需求。由表2 可知,文献[4,7-10]方案不支持核心辅助设置、属性票据和票据的不可转让性;文献[12-13]方案不支持核心辅助设置和属性票据;文献[3,15]方案不支持核心辅助设置和属性票据,也没有安全性证明;文献[6,17]方案和所提方案都支持属性票据、双花检测、不可链接性和不可伪造性,且都有形式化的安全证明,但是文献[6,17]方案都不支持核心辅助设置,且文献[17]方案不支持不可转让性。表3将所提方案与最新的2个属性票据方案[6,17]在效率上进行了比较,其中P1,P2,PT,Pe分别表示G1,G2,GT上的幂运算和双线性映射运算。相比文献[6,17]中的方案,所提方案显著降低了用户的运算量。在所提方案中,票据购买算法需用户执行13 个 G1上的运算、3 个G2上的运算和2 个双线性映射运算;票据消费算法需用户执行6 个 G1上的运算和2 个G2上的运算。所提方案中用户注册的计算量明显高于文献[17]方案,但是新用户仅需执行一次注册用户算法。
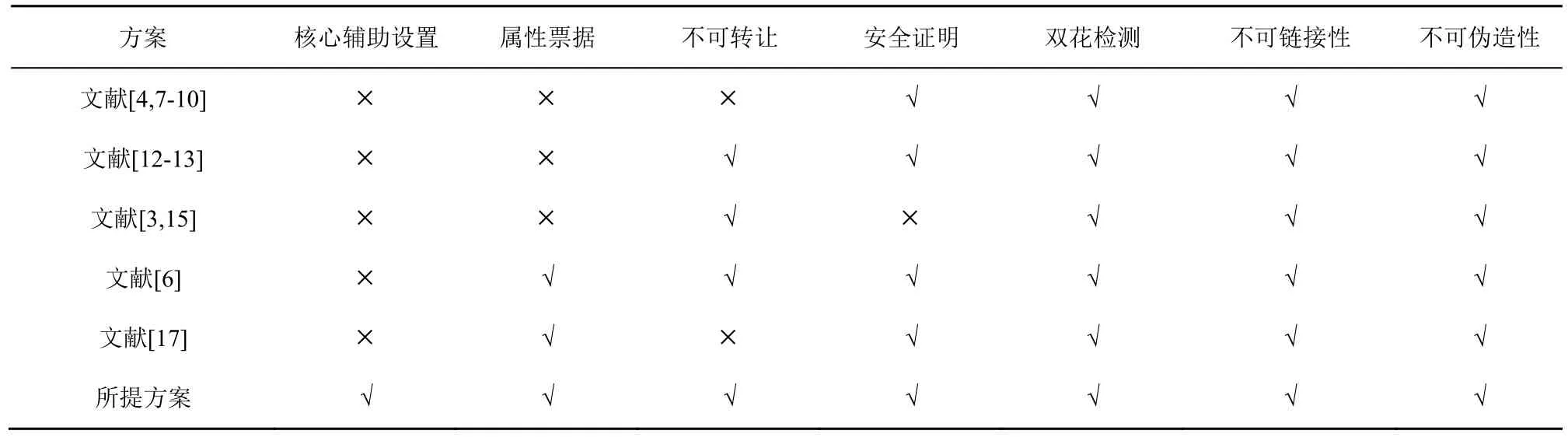
表2 功能比较

表3 效率比较
5.2 实验分析
为了准确地比较和评估所提方案的效率,使用MIRACL、Barreto-Naehrig 曲线(BN-256)[29]和SHA-256 实现了所提方案。
5.2.1 在个人计算机上的实现和对比
使用华为MateBook 作为实验平台,CPU 为AMD Ryzen-54 600 H,时钟频率为3.0 GHz;操作系统为64 位Ubuntu Kylin 16.04,运行内存为16 GB,实现语言为 C/C++,编译器为 GCC/G++。在AES-100 比特安全级别和相同实验环境下,将所提方案与最新的属性票据方案[6,17]进行了性能比较。不同之处是文献[6]方案只能使用TYPE-1 型双线性对实现,而所提方案和文献[17]方案使用了计算效率更高的TYPE-3 型双线性对实现。
表4 将所提方案与文献[6,17]方案在算法运行时间上进行了对比,其中测试时设置n=20,m=5。所提方案各个算法的运行时间显著小于文献[6]方案。与文献[17]方案相比,所提方案的票据购买、票据发布、票据消费和票据验证算法的运行效率分别提高了约200%、100%、700%、300%;所提方案的用户注册和证书发布算法的运行时间高于文献[17],但是新用户只执行一次用户注册算法。

表4 算法运行时间(单位:ms)对比
表5 是随着用户属性数量的增多,用户注册算法的运行时间对比。3 种方案的运行时间都随着用户属性数量的增加而增长。所提方案的运行时间比文献[6]方案小,比文献[17]方案大,但是新用户只执行一次用户注册算法。

表5 用户注册算法的运行时间(单位:ms)对比
表6 是随着用户属性数量的增多,票据购买算法的运行时间对比。在文献[6,17]方案中,运行时间都随着用户属性数量的增加而增长。所提方案实现了常数复杂度的票据购买算法,与文献[17]方案相比,所提方案的票据购买算法的运行效率在用户属性数量为10、20、30、40、50 时分别提高了约180%、200%、230%、250%、280%。
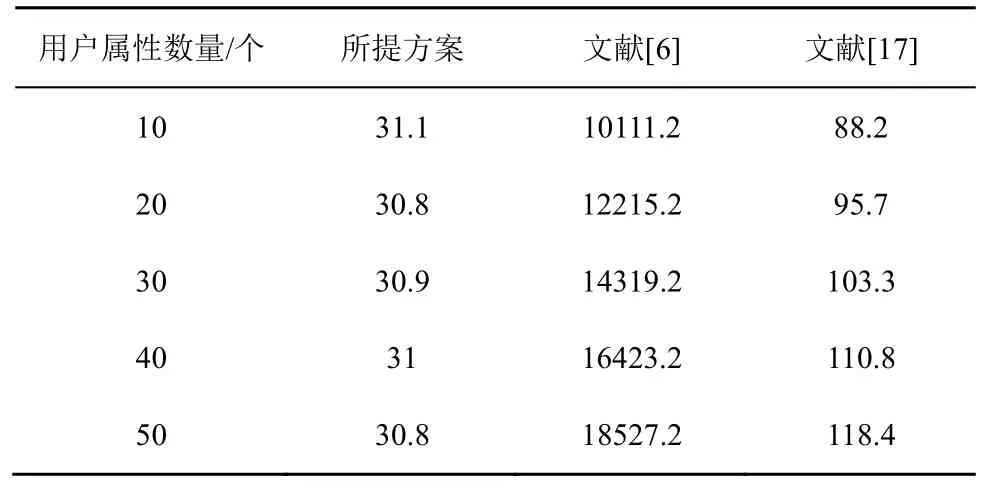
表6 票据购买算法的运行时间(单位:ms)对比
表7 是随着用户属性数量的增多,票据消费算法的运行时间对比。3 个方案都实现了常数复杂度的票据消费算法,所提方案的运行时间显著小于文献[6]方案。与文献[17]方案相比,所提方案的票据购买算法的运行效率提高了约700%。
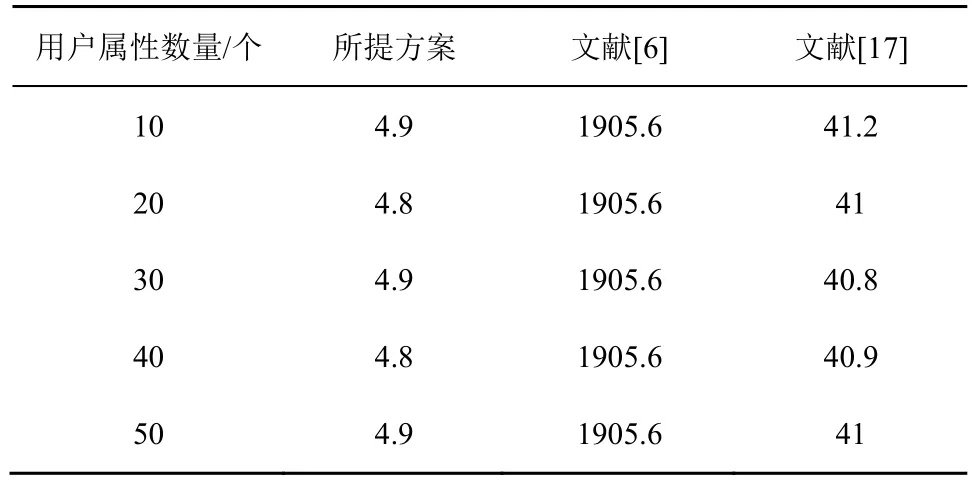
表7 票据消费算法的运行时间(单位:ms)对比
5.2.2 在智能卡和移动手机上的实现
为了评估所提方案在带智能卡的移动终端上的运行效率,本节使用智能手机作为用户的移动终端,使用个人计算机作为CA、卖方和验证方的实现平台,并在国产智能卡上测试了所提方案。其中,智能卡为爱信诺ACH512 智能卡芯片,运行内存为128 KB,设置时钟频率为40 MHz;智能手机为华为荣耀9i,CPU 为Hisilicon kirin 659 (ARMv8-A),运行内存为4 GB,主频为2.36 GHz,操作系统为Andriod 9.0;个人计算机为华为Matebook。其中,测试时设置n=20,m=5。
如图6 所示,在所提方案中执行用户注册算法需在智能卡上消耗116.7 ms,在移动终端上消耗8 250 ms,在个人计算机(执行CA 的运算)上消耗40.1 ms。
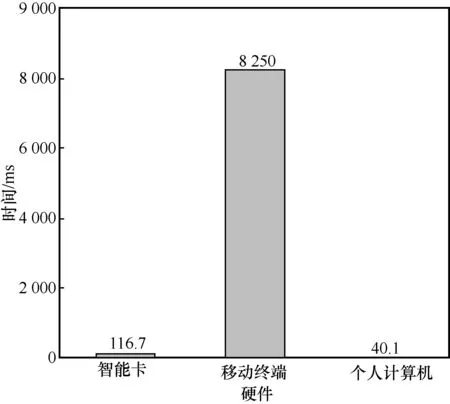
图6 用户注册算法执行时间
如图7 所示,在所提方案中执行票据购买和发布算法需在智能卡上消耗368.5 ms,在移动终端上消耗195 ms,在个人计算机(执行S 的运算)上消耗51 ms。

图7 票据购买和发布算法执行时间
如图8 所示,在所提方案中执行票据消费和验证算法需在智能卡上消耗196.6 ms,在个人计算机(执行V 的运算)上消耗38.4 ms,不需要移动终端参与任何运算。

图8 票据消费和验证算法执行时间
6 结束语
本文提出了一个适合在带智能卡的移动终端上部署的隐私保护的属性票据方案。所提方案满足不可链接性和不可伪造性的安全需求,并解决了现有电子票据系统难以在资源受限设备中部署,以及无法防止票据在未授权设备之间共享的问题。本文在个人计算机、智能卡和智能手机上测试了所提方案,测试结果证明了所提方案的高效性。

