基于多尺度特征的网络流量异常检测方法

段雪源，付钰，王坤,4，刘涛涛，李彬

（1.海军工程大学信息安全系，湖北 武汉 430033；2.信阳师范学院计算机与信息技术学院，河南 信阳 464000；3.信阳师范学院河南省教育大数据分析与应用重点实验室，河南 信阳 464000；4.信阳职业技术学院数学与信息工程学院，河南 信阳 464000）

0 引言

互联网科技的迅猛发展，不仅转变了人们的生活方式，也给网络安全带来了前所未有的挑战[1]。由于网络协议的开放性，木马、病毒等恶意软件借助互联网广泛传播，各种针对网络协议和应用程序漏洞的网络入侵攻击从未间断。这些恶意行为不仅影响网络空间的正常运行，还会扰乱社会秩序，给国民经济带来巨大损失，甚至威胁国家安全。

网络流量异常检测就是利用各种检测技术发现网络中的异常流量数据[2]，揭露网络中潜藏的攻击行为，对网络安全的防护起着关键作用。传统的异常流量检测的研究中，常用基于机器学习的检测方法包括K-Means[3]、朴素贝叶斯[4-5]、支持向量机[6]、决策树[7]以及它们的组合[8]等，但检测所用的流量特征需要人工提前完成设计。随着网络边界不断向外延伸，以及各种网络服务的激增，网络流量数据呈现多样性、爆炸式增长。传统的机器学习方法在应对海量、高维、动态的网络流量时，往往表现出特征设计困难、误报率高和泛化能力弱等问题。

深度学习有着强大的表征能力，能够从原始数据中自主地提取特征，完成分类判断，被应用于自然语言处理、机器视觉、智能诊断等领域。在网络流量的异常检测中，深度学习技术也有着广泛的使用，循环神经网络（RNN，recurrent neural network）常被用来捕捉流量数据中当前连接与之前连接的潜在联系[9]，即时间信息的关联性；卷积神经网络（CNN，convolutional neural network）通过卷积计算捕捉流量信号在频域上信息的相互关系[10]。此外，还有很多生成式神经网络被用来解决流量样本类别不平衡的问题，主要有生成对抗网络（GAN，generative adversarial network）[11]、自编码（AE，autoencode）神经网络[12]，它们利用正常流量建模，可以很好地完成正常流量的重构，而异常流量在重构时将会产生较大的误差，利用这个误差可进行异常流量的判别。虽然这些基于神经网络结构的异常检测模型能够完成特征网络环境中异常识别问题，但模型本身大都是单层体系结构，即只利用了流量在单尺度的特征，并没有充分利用流量数据在不同尺度下的多样性特征，存在着检测精度低、误报率高、对不同网络环境的适应性弱等问题。

针对当前基于深度学习的网络流量异常检测方法大都只用到了流量的单尺度信息，没有充分利用网络流量在不同尺度下多样性特征信息的问题，本文提出了一种基于多尺度特征的网络流量异常检测方法。多尺度特征具有2 个维度的含义：一是流量的观察跨度，由一些不同尺度的滑动窗口对流量序列划分后获取到多个观察尺度的子序列特征；二是时频域维度，利用小波变换对流量序列进行逐级分解、重构，得到流量序列多层级的特征。原始流量经过滑动窗口、小波变换后得到多个不同尺度的重构序列。利用正常流量的重构序列数据训练链式堆叠自编码（SAE,stacking autoencode），SAE 学习到正常重构序列的特征分布，并构建特征空间，该空间可完成对输入序列进行再次重构。由于使用正常流量对SAE 建模，因此SAE 可对正常样本很好地重构，但对于输入的异常样本，SAE 将不能有效地重构，此时重构样本与输入样本之间存在较大的重构误差。分类器将重构误差与判定阈值进行比较，大于阈值的样本则被判定为异常流量。

1 相关工作

研究发现，正常流量和异常流量的时变信号在频率上存在较大差异，因此有学者尝试利用流量的频域特征设计异常检测的方法，较典型的是以傅里叶变换或小波变换为基础的检测方法。Brynielsson等[13]对网络流量进行离散傅里叶变换后，利用频谱分析的方法评估不同攻击场景下模型的检测效果。何炎祥等[14]以数据包数量为研究对象，通过小波多尺度分析，结合低速率拒绝服务攻击规律，提取攻击流量特征指标，作为攻击流量异常检测的依据。Cheng 等[15]利用离散小波变换将原始流量变换为不同频域下的数据序列，为异常检测提供了网络流量的多样性信息。Wang 等[16]将小波频率分析嵌入深度学习框架，利用小波分解技术在频率学习中的优势，提取网络流量中的频域特征进行无监督的异常检测。Fouladi 等[17]提出基于离散小波变换和AE 神经网络的软件定义网络（SDN,software defined network）分布式拒绝服务攻击检测方案，利用小波变换中提取流量的统计特征，AE 神经网络根据交换机流表中的平均命中率启动对攻击的检测，取得了较好的效果。然而，上述研究只计算了流量在某一观察跨度的特征，没有充分利用流量在不同观察跨度上的关联信息。而网络安全事件在时间上有很强的关联性，研究表明，网络流量聚集观测的跨度能够对检测结果产生较大的影响[15]。

利用深度学习检测大规模网络流量中的异常是当前研究的热点，按使用神经网络模型的结构可分为单结构模型和多结构模型。单结构模型是指使用单一类型神经网络搭建的检测模型，包括RNN、CNN、AE 或GAN 等网络结构。Albahar[18]针对SDN安全方面存在的设计缺陷，提出了一种基于新的正则化技术的RNN 模型，在不影响网络性能的情况下，实现对SDN 入侵的有效检测。Pei 等[19]提出了一种基于长短期记忆（LSTM,long short-term memory）结构自编码的网络流量异常检测方法，在保护隐私的前提下对数据进行聚合，构建针对网络流量异常的个性化联合检测框架，提升了模型对不同数据的泛化能力。Zong 等[20]设计的DAGMM 将深度AE 压缩网络和改进的高斯混合模型（GMM,Gaussian mixture model）相结合，实现数据降维和密度估计同时优化的异常检测，常被用来检测网络流量中的异常数据。Yang 等[21]提出集成式无监督网络异常检测方法，使用正常网络流量数据训练自编码器，并将自编码器每层输出的马氏距离与重构损失进行合并，计算出检测流量数据的异常得分，将大于阈值的判定为异常流量，性能优于单独使用马氏距离或重构损失的模型。除了自编码网络，GAN也是生成式模型中常用的结构，Geiger 等[22]提出的TadGAN 异常检测模型就是典型的生成式模型，它利用正常数据训练双向GAN（BiGAN,bidirectional GAN）模型；训练好的模型能较好地完成对正常数据样本的重构，对异常样本则无法实现有效重构，TadGAN 已经成为异常检测领域性能比较的基准之一。类似地，Patil 等[23]提出一种智能化的轻型网络流量异常检测框架PCA-BiGAN，利用主成分分析（PCA,principal component analysis）对原始数据进行特征提取和降维，采用双向GAN 检测异常的网络流量，验证了较少的特征有利于提高模型的检测效率。邹福泰等[24]提出基于GAN 的僵尸流量特征生成算法，分别从时间和空间2 个维度产生僵尸网络特征样本，扩充僵尸网络训练集，并利用GAN的反馈机制提升检测的准确性。

随着深度学习的发展，很多研究人员尝试设计多结构模型，即由不同类型神经网络组合搭建的模型。Chen 等[25]提出的DAEMON 也是基于重构的模型，与TadGAN 不同的是，DAEMON 是由变分自编码器（VAE,variational autoencoder）与GAN 组合构建的，VAE 得到的是对输入数据的重构而非对数据本身的重构，因此DAEMON 对异构数据有较强的适应性。麻文刚等[26]使用3 层堆叠LSTM 网络来提取不同深度的网络流量特征，并利用带跳跃连接线的改进型残差神经网络对LSTM 进行优化，改善了深度神经网络中的过拟合与梯度消失的缺点。Chouhan 等[27]提出基于信道增强和残差学习的深度卷积神经网络（CBR-CNN,channel boosted and residual learning based deep CNN）模型，利用多个SAE 对原始信号进行多路映射实现信道增强，再利用残差卷积网络学习各个信道的特征，为流量分类提供依据。Yang[28]将SAE 与LSTM 神经网络相结合，由多个串联的SAE 提取连续流量的有效特征，LSTM 网络提取有效特征的时间结构，同时为了提升检测效率，对检测数据采取去除介质访问控制（MAC,medium access control）地址的预处理操作。Ullah 等[29]将卷积神经网络和循环神经网络相结合搭建混合深度学习模型，利用卷积神经网络学习输入数据特征，由LSTM、双向LSTM 和门控循环单元（GRU,gated recurrent unit）构成新的RNN 轻量级二值分类模型，实现对物联网中异常流量的检测。

当前的网络流量异常检测方法中，无论是单结构模型还是多结构模型，大多都是以抽取流量中的细粒度特征来获得更高层次的时间关联性信息，而没有考虑在不同尺度下的影响，很难确定模型的放样深度，因此难以生成最优结构。另外，这些方法仅使用了网络信号在某一频域的特征，并没有充分挖掘出它们的多频域信息。事实上，高频的特征更能反映流量数据中细粒度的差异性；而低频的特征是信号的原生状态，反映流量数据的未来趋势走向[30]。因此，网络流量在不同的观察尺度上表现出不同的行为特征，在不同的频域尺度上反映出信号的原生状态和细粒度差异。虽然有研究曾将小波变换和序贯模型结合使用[31]，使检测的性能得到了改进，但只进行了初步的组合，小波变换只是用于缩短序列长度，而各层次的小波分解结果是相互独立的，且没有考虑到多尺度关系的问题。

2 模型

为充分获取和利用网络流量的多尺度特征信息，提升网络流量异常检测的准确性，本文把小波变换与深度学习相结合，提出了基于多尺度特征的异常流量检测模型，其架构如图1 所示。首先，网络流量数据序列被不同尺度的滑动窗口划分为不同观察尺度的多个子序列，利用小波变换技术对每个尺度下的所有子序列进行分解、重构，生成不同层级的重构序列数据；然后，利用训练好的链式SAE 对每个重构序列进行特征提取和转换生成重构序列，通过计算重构序列与原始序列的重构误差进行异常判定，分类器得出每个观察尺度下的分类结果；最后，根据“加权投票”策略汇总各观察尺度上分类结果，作为最终检测结果输出。模型主要由输入模块、多尺度特征分类器（MFC,multiscale feature classifier）和输出模块组成。输入模块主要完成原始流量数据的预处理，删除缺损、冗余的数据，将字符型特征转换为数值型；为了便于运算，采用Max-Min 的方法将各属性值做归一化处理。MFC 模块是异常检测模型的核心，主要完成预处理后流量的多观察尺度划分、多层级序列重构、重构误差计算、异常流量样本的初步判定等任务。输出模块主要是根据规则汇总各尺度分类器的结果，并完成最终检测结果的输出。

图1 基于多尺度特征的异常流量检测模型架构

2.1 多观察尺度划分

大观察尺度可以展示信号数据的全局趋势，而小尺度则提供更多细节信息。因此，本文利用滑动窗口将流量数据划分为不同观察跨度的子序列，以获得原始流量的多样性信息。滑动窗口主要是将流量序列截取为不同观察尺度的子序列，为了避免子序列间重叠，将滑动窗口尺度与步长均设置为S，即观测流量的窗口尺度。

2.2 多层级序列重构

为得到原始流量的多层级重构序列，本文使用多级离散小波变换（MDWT,multilevel discrete wavelet transform）将原始流量数据在不同层级上进行分解与重构。离散小波变换是利用有限区间的母小波ψ(x)通过平移和缩放而将原始信号分解为一组小波基函数{ψa,b(x)}，表示为

其中，a为缩放参数，b为平移参数。

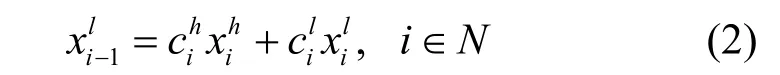
其中，f(·) 表示重构函数，可分别通过对升采样得到。当j取不同值时，原始数据序列即可变换为不同尺度的重构序列。图2 展示了数据经小波滤波器进行多级分解与重构的过程，其中，H1和H2为高通滤波器，L1和L2为低通滤波器。

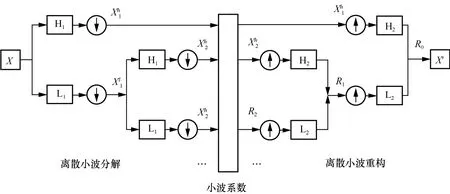
图2 多级分解与重构的过程

2.3 重构误差计算

使用SAE 计算经过编码、解码后的重构序列与原始输入序列之间的误差。SAE 是由多个AE 堆叠而成的多层神经网络，其结构如图3 所示。

图3 SAE 结构

前层AE 编码器输出的潜在变量作为后层AE编码器的输入，这种连接方式可在原始特征向量到目的特征向量转换的过程中，帮助捕获原始特征空间的更多细节。AE 是前馈型的神经网络，由输入层、隐藏层、输出层组成，通常输入层和输出层具有相同大小，AE 将输入映射到潜在特征空间（编码），再由潜在空间映射回重构输出（解码），此编码、解码过程可表示为

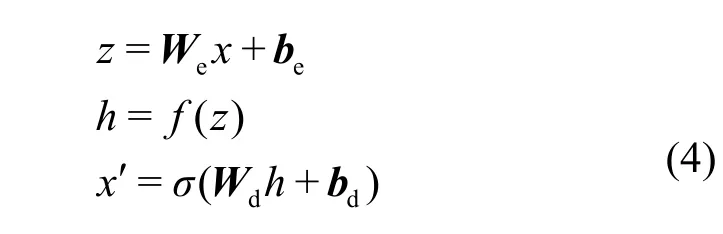
其中，x为给定输入，h为潜在变量，x＇为x经编码、解码后的重构输出；f(·)、σ(·) 为各自的激活函数；We、Wd和be、bd为编码器、解码器的权重和偏置；AE 通过最小化重建误差 min(x-x＇)2进行优化。利用正常流量数据对SAE 进行训练，采取贪婪分层的方法，可分为预训练和微调2 个阶段。

预训练阶段。使用无监督方法，利用最小化重建误差的均方误差，对AE 逐层进行初步训练。训练好的前层AE 将学习到的潜在表示作为后层AE 的输入，训练好的后层AE 再将学习到的新表示继续向后传递，帮助下一层AE进行训练，直到所有AE 完成训练，这种预训练的做法可以为整个SAE 提供良好的初始参数。

将训练好的编码器逐个连接，并将对应的解码器按相反顺序连接，构造链式SAE 结构，如图4 所示。

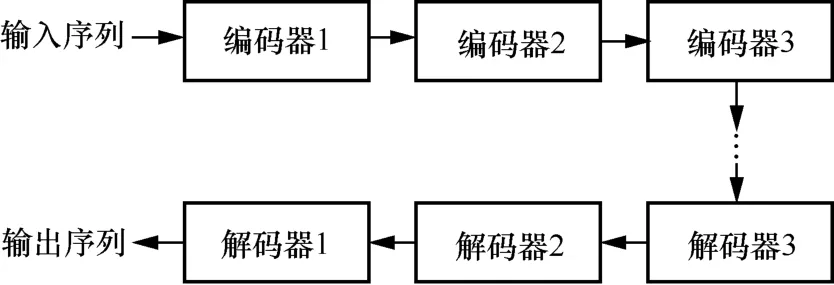
图4 链式SAE 结构

令φi和φi分别为第i个AE 的编码器函数和解码器函数，那么SAE 的编码过程可以由各AE 编码器的转换函数叠加表示，即

其中，◦为联合函数，xw为原始输入x经过一系列转换后从第w个激活函数输出的高阶特征表示。解码过程则按相反的顺序，利用各个AE 的解码器转换函数对xw进行反向重构，其过程可表示为

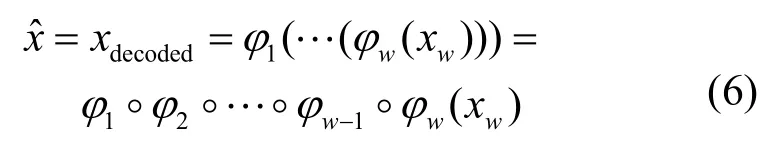
由于SAE 的编码器和解码器是在正常数据上训练，可对正常样本进行有效的重构，对异常样本重构则会产生较大偏差，重构样本和原始样本对应分量之间的绝对差值为整个样本的重构误差，可表示为

其中，xi为原始流量特征的第i个分量；为第i分量的重构特征；ei为该分量经过小波变换的多层级分解、重构，再由SAE 编码、解码后计算出的重构误差。各观察尺度的分类器将得到的重构误差与本尺度的异常判定阈值比较，当重构误差大于阈值时，则将该观察尺度的初步检测结果暂时划分为异常。

判定阈值的设定，参照“三西格玛”准则，将验证集的正常样本输入训练好的模型，将验证集所有正常样本产生的重构误差的均值加3 个标准差作为异常判定的阈值，即Sthreshold=μ+3σ。

2.4 异常流量样本的初步判定

本文采取“加权投票”的方法汇总各观察尺度的初步检测结果作为流量异常检测的最终判定结果。由于大的观察尺度反映了网络流量长时的关联性，展示了数据的全局趋势；而小的观察尺度反映了网络流量的局部相关性，提供更细节的流量信息。因此，相对大的观察尺度提供初步检测结果可被赋予更大的权重，而对小观察尺度的初步检测结果可被赋予相对小的权重。对N个观察尺度的模型，将观察尺度按从小到大排列分别被赋予1～N，则第i个观察尺度初步检测结果hi(x)的权重可表示为

将异常的初步检测结果设置为“1”，正常设置为“0”，汇总初步检测结果后可得到最终的汇总检测值为

将检测该值与汇总阈值比较，若不小于汇总阈值，则判定输入样本为异常。汇总阈值利用超参数搜索法设置，将验证集中全部样本输入训练好的模型进行测试，当模型的异常检测性能指标F1 值达到最大时确定。

3 实验及结果分析

3.1 实验环境

本文实验在支持GPU 的设备上进行，GPU 型号为GeForce RTX 3090，具有24 GB 的RAM。软件为Ubuntu 18.04LTS、CUDA11.2、Pytorch1.8。

3.2 评估指标

实验的最终目标是将网络中的正常流量和异常流量进行区分，因此异常检测工作实际是二分类问题，可将异常流量定义为正样例，正常流量定义为负样例。为全面评估所提方法对网络中异常流量的检测性能，使用准确率 Accuracy、精确率Precision、召回率Recall、误报率（FPR,false positive rate）以及F1 值等5 个检测指标，计算式分别为

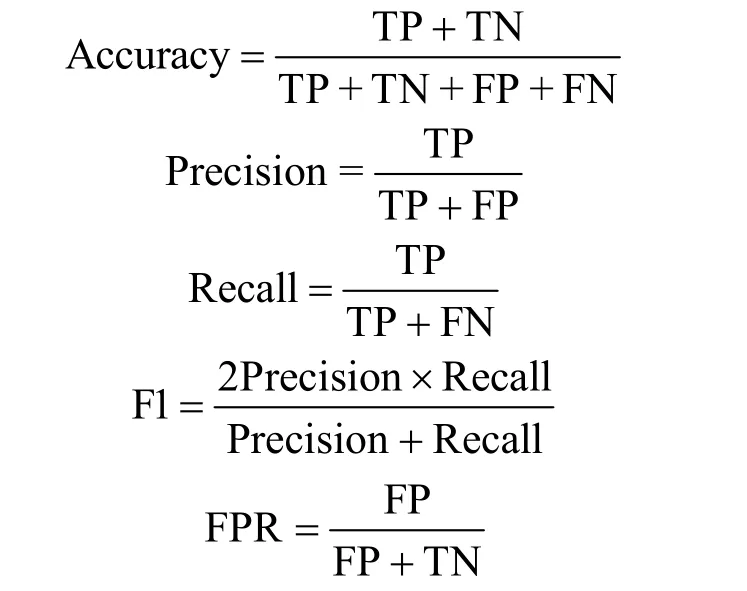
其中，TP、TN、FP、FN 为样例的真实分类与预测分类的相互关系，真实分类与预测分类的关系矩阵如表1 所示。

表1 真实分类与预测分类的关系矩阵

3.3 数据设计

3.3.1 数据集构建

为了检验MFC 的分类性能，本文在多个网络流量数据集上进行评估测试，使用4 个公开网络流量数据集KDD99、NSL-KDD、UNSW-NB15 以及CIC-IDS2018，这些数据集都被划分了训练集、测试集，并标注了标签。为缩减运算开销，使用这些数据集的部分数据作为本文研究的原始数据，其中，KDD99、NSL-KDD、UNSW-NB15 这3 个数据集使用各自的子集，CIC-IDS2018 则使用Thursday-01-03-2018 子数据集。所选的数据子集的基本信息如表2 所示，包括样本总数、正常样本数、异常样本数、特征数等信息，另外，数据集中每个异常位置也都是已知的。

表2 原始网络流量数据集信息

由于训练模型和计算阈值仅使用正常流量，故将全部正常样本按40%、30%、30%的比例随机划分，其中，40%的正常样本作为训练集；30%的正常样本作为验证集的正常样本，原训练集的异常样本作为验证集的异常样本；剩下30%的正常样本与原测试集中异常样本组合为新的测试集。表3 汇总了新构建的各数据集的基本信息。每个数据集都各有特点，使异常检测研究更具挑战性，同时有助于确认模型的有效性以及对不同网络数据的适应性。

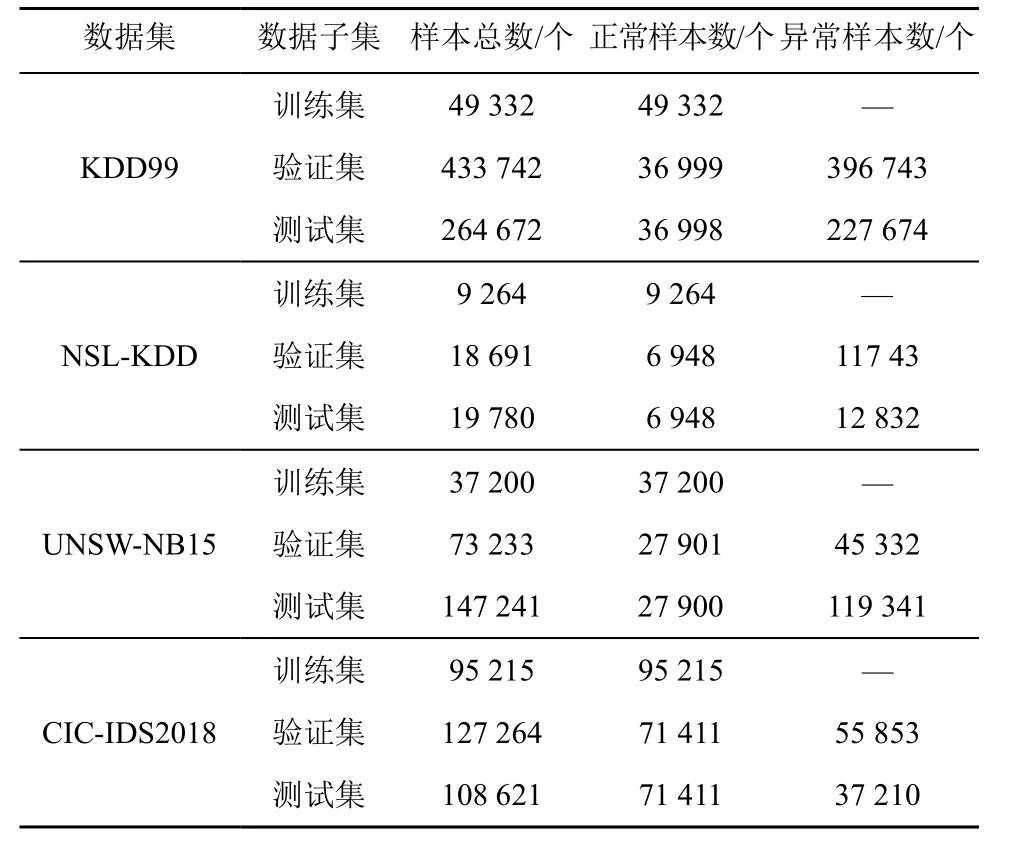
表3 新构建的各数据集的基本信息

3.3.2 数据预处理

数据预处理是为保证流量数据的可读性和统一性而进行的数据清洗、文本数值化、流量匿名、数值归一化等操作。

1) 数据清洗。真实网络环境中抓取的流量数据，可能存在重复或残缺的无效数据，需要利用数据清洗技术对这些冗余和缺失数据进行清除。

2) 文本数值化。原始流量数据的特征值并不完全是数字，还有些可能是用字符表示的，因此需要将这些字符特征做one-hot 编码，转换成相应的离散数值，以便参与运算。

3) 流量匿名。各流量特有的IP 地址和MAC地址等信息可能会影响分类特征提取。为消除这些因素的影响，使用随机生成的新地址替换原来的地址。这一步是可选的，如果待检测的流量来自同一个网络环境则不需要此操作。

4) 数值归一化。不同属性特征的量纲不同，特征值的取值范围也不尽相同，数据差异较大时会影响模型训练，以及最终检测结果的精确，在实验前使用Max-Min 方法对数据进行归一化处理，使特征值分布在[0,1]区间。

3.4 实验结果与分析

3.4.1 单尺度窗口模型性能检测实验

本节实验主要检验模型在单一观察尺度（单尺度窗口）下的性能，滑动窗口的尺度设置为800；使用DB3 小波滤波器，小波分解的最大分解层级为6 级；SAE 结构为3 层AE 链式连接，链式SAE 的结构参数如表4 所示。

表4 链式SAE 的结构参数

使用Adam算法优化，学习率为0.000 01，BN=16，使用NSL-KDD 的训练集对模型进行100 次完整训练。模型训练完成后达到稳态，重构误差不再随训练次数增加而明显减小。模型训练好后，利用验证集数据计算出异常判定阈值和汇总阈值。

为缓解样本类别不平衡可能带来的计算偏差，客观地评价模型的性能，采用五折交叉运算的方式检验 MFC 对异常流量的检测能力。具体是将NSL-KDD 的测试集数据平均分为5 部分，每次选择4 部分进行测试，最终检测结果取5 次测试指标的均值，单尺度窗口模型在NSL-KDD 上的检测性能如表5 所示。通过检测结果可以看出，单尺度窗口下的MFC 模型在5 次检测中对异常样本的召回率均超过94%，准确率和精确率均在90%以上，平均F1 值为0.938 6，平均误报率为5.15%，说明所提方法能够较有效地检测出NSL-KDD 数据集中的异常样本。

表5 单尺度窗口模型在NSL-KDD 上的检测性能

3.4.2 多尺度窗口模型性能检测实验

本节的实验主要检验模型在3 个不同观察尺度（多尺度窗口）下的检测性能，仍然使用DB3 小波滤波器，滑动窗口大小分别设置为600、800、1 200，其余实验条件设置同3.4.1 节。仍然使用NSL-KDD训练集数据对模型进行100 次的完整训练；利用验证集数据计算出异常判定阈值和汇总阈值。利用测试集数据进行性能检验，仍采用五折交差运算的方式获取最终结果。单尺度窗口模型与多尺度窗口模型检测性能对比如图5 所示。

图5 单尺度窗口模型与多尺度窗口模型检测性能对比

从图5 可以看出，在相同的最大分解层级和检测数据集下，多尺度窗口模型对异常样本的检测性能无论是检测精确率、准确率还是召回率都高于单尺度窗口模型，并且能够取得更低的误报率。这说明多个观察尺度的流量特征相对于单一尺度特征更能够反映流量数据本质的区别，对流量分类有着积极作用。直观的解释为，观察尺度越多，包含的信息越丰富，挖掘出的特征关联性越充足，对流量中异常的发现有着积极作用。

3.4.3 多尺度窗口多变换层级模型性能检测实验

本节实验主要为了验证在多尺度窗口下，不同的分解层级对异常检测性能的影响，将小波分解的最大分解层级分别取2、4、6、8，其余模型设置和训练条件与3.4.2 节的实验条件相同。由于不同的分解层级需要单独进行训练、求取阈值和检验性能，在3.4.2 节实验中已经在最大分解层级为6 时进行了检测，因此本节的实验还需在最大分解层级为2、4 和8 时对模型进行训练，同样还需利用验证集分别求出对应的阈值，再用测试集进行性能检验。多尺度窗口多变换层级模型检测性能对比如图6 所示。

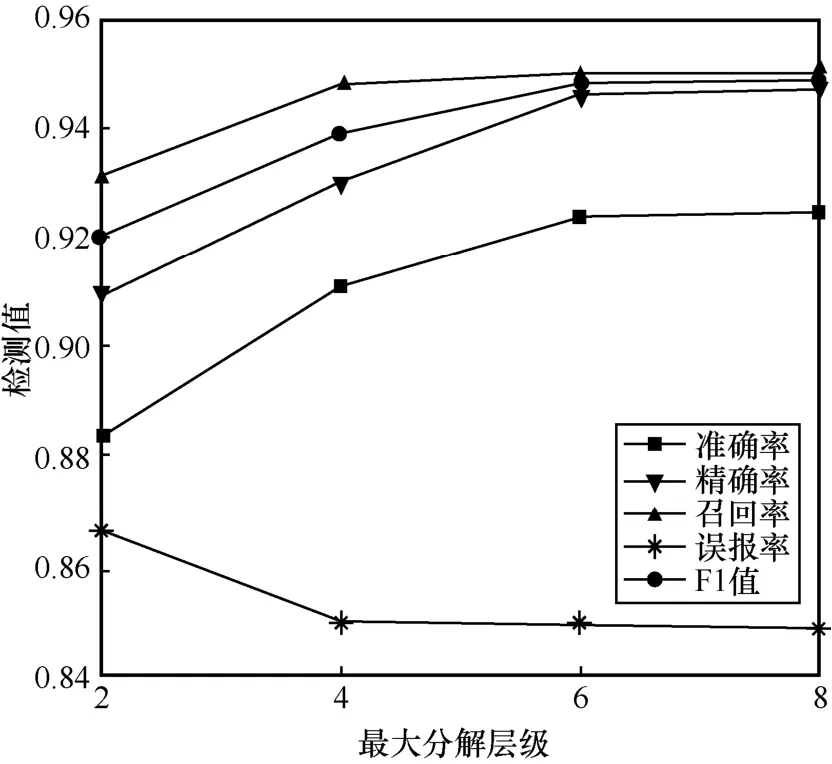
图6 多尺度窗口多变换层级模型检测性能对比

从图6 可以看出，随着分解层级的增加，模型的准确率、精确率及F1 值等检测指标总体呈现逐步上升趋势，误报率也不断下降，即更多的尺度特征信息可以让模型的检测性能更加出色。然而，最大分解层级为6 时的异常召回率为95.06%，最大分解层级为8 时的召回率为95.05%，出现这种情况是由于变换尺度过深，产生了过多的重构序列，导致训练时产生过拟合，从而引发模型的泛化能力退化。另外，最大层级为6 和8 时的F1 值较接近，2 个模型的总体性能相当，对比其他2 个分解层级的检测性能，考虑到计算开支问题，可以选择3 个尺度窗口和最大6 个变换层级作为MFC 模型的最优结构。

3.4.4 与典型检测方法的对比实验

为了检验MFC 模型对不同数据的泛化能力，除了NSL-KDD 外，本节还在KDD99、UNSW-NB15 和CIC-IDS2018 几个公开数据集上进行实验，同时与Tad-GAN[22]、DAGMM[24]以及CBR-CNN[26]等经典的检测模型性能进行比较，其中，Tad-GAN 为双GAN 结构的生成式模型，常作为时间序列异常检测研究中的比较基准；DAGMM 为深度自编码高斯混合模型，因巧妙地把降维与密度估计结合在一起训练，避免了模型陷入局部最优，受到学术界的关注；CBR-CNN 为采用了信道增强技术的SAE 与CNN 的多结构模型，也经常被作为参照来评估其他流量异常检测模型性能。表6 展示了不同模型在4 个数据集上的异常检测性能。

表6 不同模型在4 个数据集上的异常检测性能

从表6 可以发现，所提的基于多尺度特征的异常检测方法（MFC）在NSL-KDD、UNSW-NB15和CIC-IDS2018 这3 个数据集上的精确率、召回率和F1 值均最高，在KDD99 数据集上的召回率也是最好的，并且在4 个数据集上的精确率、召回率和F1 值三项指标的均值都为最高。MFC 在不同数据集上的优异表现，说明MFC 能较好地适应不同类型的网络流量数据。虽然这4 个数据集产自不同的网络环境，具有不同的特征数量和攻击类型，但从广义上来讲它们都是在计算机网络中生成的，具有网络流量数据的共性时频域特征。可以说，本文方法不仅可以从原始数据的低频分量中获取到原生态的本质特征，还能从高频分量中提取出流量数据的细粒度差异，具有很好的检测性能，同时也表现出对异构数据较强的泛化能力。

另外，DAGMM 在KDD99 和NSL-KDD 这2 个数据集上表现也比较出色，这是由于DAGMM 建模之初就使用KDD 数据集，经过多次优化调整，因此对于KDD 系列的数据集具有较好的适应能力。观察表6 还可以发现，除了DAGMM 和MFC 外，Tad-GAN 和CBR-CNN 模型在UNSW-NB15 数据集上的综合指标F1 值均高于另外3 个数据集。其原因可能是由于UNSW-NB15 测试集中异常样本占比较大，约为81.05%，这种样本类别的不平衡性给以这些发现异常为目的检测任务带来了便利。而对于同样是异常样本占比高达86.02%的KDD99数据集，检测表现不佳的原因与数据集本身的特征量有关，虽然KDD99 中的特征数据有41 个，真正独立的特征量较少。另外，时间信息是网络流量异常检测的重要依据，KDD99 的41 个特征中虽然有10 个特征与时间有关，但是除了第一个连接时间的特征外，其余9 个均是连接前2 s 的统计特征，包括5 个同主机的连接特征和4 个同服务的连接特征，且它们间关联性很强，故而出现了“信息冗余”。而UNSW-NB15的49 个特征中有9 个与时间有关，除了链路的连接时间外，还包含数据包到达时间间隔等特征，以及一些数据包的其他特征，这些特征是区分正常流量和异常流量最主要的特征，也是各模型对UNSW-NB15 的检测结果相对其他数据集更加出色的原因。

3.4.5 与新的检测方法性能对比

本文还与3 种新检测方法进行了性能对比，分别为基于K-Means 聚类与支持向量机混合概念漂移的网络异常检测技术K-Means &SVM[8]、基于主成分分析与双GAN 相结合的流量异常检测方法PCA-BiGAN[23]、以重建损失和马氏距离（RL-MD,reconstruction loss and Mahalanobis distance）为损失函数的自编码器网络流量异常检测方法[21]，具体结果如表7 所示。从表7 可以看出，MFC 相比其他几种方法在对应数据集上的表现似乎并不出众，只有在UNSW-NB15 数据集上的召回率和F1 值指标优于RL-MD；在KDD99 和NSL-KDD 数据集上的性能不如另外2 个模型。虽然K-Means &SVM 方法在NSL-KDD 上表现出色，但是作为机器学习的检测方法，需要提前设计数据特征才能达到较好的检测效果，且无法做到对未知异常的检测。MFC 是深度学习模型不需要过多的特征工程辅助；另外，由于MFC 使用正常数据建模，原则上还具备对未知异常流量的检测能力。PCA-BiGAN 在KDD99 上的检测性能也优于本文方法，但仔细对比可以发现，PCA-BiGAN 的性能只是略好于MFC，2 种检测方法的性能差距并不大，并且MFC 的精确率和召回率都在92%以上，MFC 在KDD99 的表现也不错。总体看来，本文方法能够自动提取流量数据特征，具有较好的检测性能，对不同数据有较强的泛化能力，还可对未知异常进行检测。

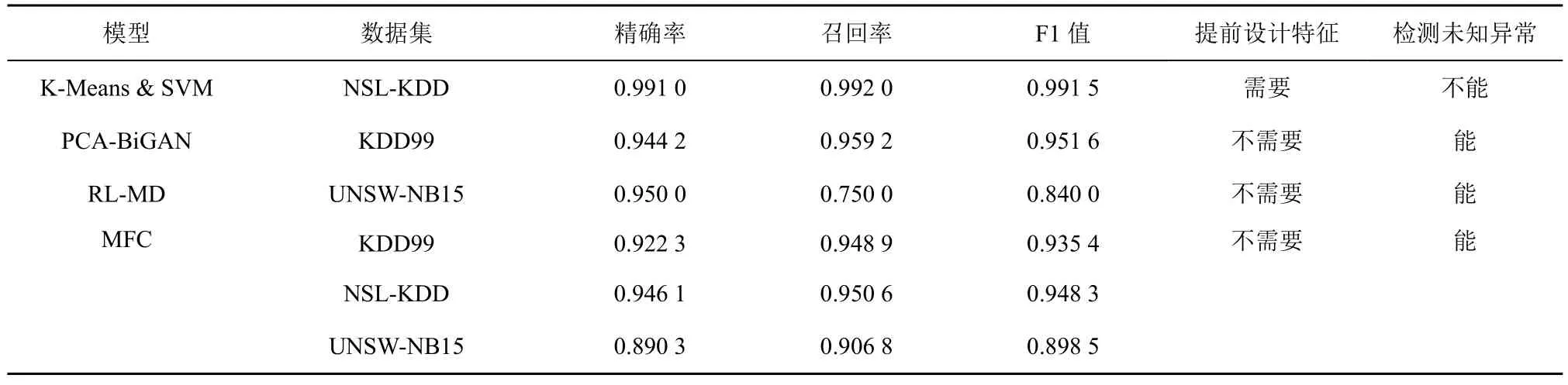
表7 与新检测方法的性能对比

4 结束语

本文提出了一种基于多尺度特征的网络流量异常检测方法，通过提取网络流量在不同观察尺度和变换层级下的多尺度特征，以获取流量特征的多样性信息，用于识别和检测网络中的异常流量。本文主要利用滑动窗口和小波变换技术，捕获网络流量不同观察尺度和变换层级下的特征信息；利用链式SAE 学习正常流量样本的分布，构建特征空间，在特征空间可生成输入样本的重构样本。待测数据输入到训练好的模型，通过比较重构样本与输入样本之间的差异得到重构误差；各尺度的分类器将重构误差与阈值进行比较，进行初步的异常判定；最后按照“加权投票”的方式，对各尺度的初步判定结果进行汇总，完成最终结果的判别和输出。

实验结果证明，本文方法能够充分挖掘原始网络流量的多样性信息，有利于更好地发现网络中的异常数据，并且较其他传统的检测方法具有更加出色的检测性能和泛化能力，为实现大规模非平衡类别网络流量的异常检测提供了新思路。同时也验证了网络流量数据在不同尺度特征下能够表现出差异性的行为模式，与仅从最细粒度的流量序列中提取特征相比，充分考虑流量数据多尺度信息，可在更大范围挖掘流量数据潜在的深层特征，对于异常检测具有积极影响。