超声波透金属通信中信道交织器的设计和性能分析

许琳森，杨维，田洪现

（北京交通大学电子信息工程学院，北京 100044）

0 引言

近年来，有关超声波透金属（UTM,ultrasonic through-metal）通信的研究引起了广泛关注[1-2]。由于金属的趋肤效应，电磁波无法有效穿透金属，如果采用在金属上钻孔的有线通信方式，则破坏了金属结构的完整性，带来了潜在风险，如有毒化学品的泄漏、压力或真空的损失等。因此，许多研究利用超声波实现穿透金属的通信或功率传输[3-14]，例如，利用超声波监测航空航天器的机身外部的环境变化[12]，利用超声波监测大型航运集装箱内部的环境变化[13]，以及利用超声波穿透反应堆安全壳的无线通信[14]等。

大多数研究采用正交频分复用（OFDM,orthogonal frequency division multiplexing）技术来克服UTM 信道的频率选择性衰落，避免了使用复杂的均衡技术，并且可以实现高速的数据传输。除了频率选择性衰落，噪声也会影响UTM 通信系统，使信号在传输过程中出现错误。

为了提高UTM 通信系统的可靠性，通常采用信道编码技术。信道编码通过在数据中加入冗余比特，增强了数据抵抗噪声和频率选择性衰落的能力，同时，将信道编码与高阶调制技术相结合可以避免添加冗余比特所导致的信道频谱效率降低，这被称为编码调制技术。编码调制技术仅能纠正少量不连续的比特错误，而对于较长的连续比特错误，可以采用信道交织技术，在不增加额外冗余比特的情况下提高信道编码性能[15]。文献[16]提出了比特交织编码调制（BICM,bit interleaver coded modulation），文献[17]从信息论的角度对BICM 进行了分析，发现BICM 比网格编码调制具有更优异的误比特率（BER,bit error rate）性能。将BICM 与OFDM相结合是一种能提高频率分集且复杂度较低的有效方法[18]。

在频率选择性衰落信道中，可能有多个子载波处于深衰落，这会产生连续的错误比特，而交织器可以将错误比特较均匀地分散到整个编码比特序列中，进而降低译码的比特错误概率。文献[19]研究了一帧OFDM 信号的交织，其中，一帧OFDM 信号具有多个OFDM 符号，每个OFDM 符号有多个子载波，交织器必须考虑所有子载波的联合交织。由于UTM 信道具有准静态的特性，多个OFDM 符号的联合交织所带来的时间分集增益较小。由于UTM信道具有频率选择性，一个OFDM 符号内的比特交织可提供较高的频率分集增益，因此，UTM 信道交织器主要在频域上进行。

文献[20]基于BICM-OFDM 系统提出了一种卷积编码的近似BER 理论表达式，其中比特交织在一个OFDM 符号内进行。文献[21]将具有强和弱比特度量的比特相互组合，获得了显著的BER 性能提升，仿真结果表明该方法优于一般的交织器。文献[22]提出了一种基于BICM-OFDM 的规则块状交织器的优化方法，仿真结果表明，在瑞利信道下，优化的规则块状交织器比随机交织器和一般的块状交织器具有更低的BER。带有高阶调制的BICM在比特映射时产生了不等差错保护（UEP,unequal error protection），即符号中位置不同的比特受到噪声的影响不同，从而产生不同的误比特率。文献[23]分析了基于正交振幅调制（QAM,quadrature amplitude modulation）的BICM 传输系统中的UEP，提出了一种可提高2 dB 信噪比增益的设计方案，降低了UEP 对误比特率的影响。大多数研究都是对矩形交织器进行优化，以得到性能更优的交织器，这些优化大都基于以下2 个准则：准则一，在比特位置向量中，强比特位置和弱比特位置应该被均衡排列[18,20]；准则二，强比特位置和弱比特位置应该按自由距离最小的错误事件排序[20,23]。以上分析的各种交织器及其优化方法并没有考虑到具有严重频率选择性衰落的UTM 信道，因此，必须设计一种适用于UTM 通信的信道交织器，以降低UTM 通信编码传输的误比特率。

本文提出了一种UTM 通信编码传输的多输入信道交织器，并对其BER 性能进行了仿真分析。所提出的信道交织器利用多输入交织器的分组思想，将处于UTM 信道不同振荡周期的编码比特进行分组，不仅使各个子交织器中的比特所经历的信道功率增益变得平缓，而且保持了编码比特的比特位置序列，在一定程度上降低了UEP 的影响。随后对各组比特进行移位操作和矩形交织，进一步分散连续的错误比特。由于UTM 信道是恒参信道，且信道频率响应的表达式较复杂，对UTM 通信编码传输的性能分析难以得到准确的解析表达式，因此，采用随机选择错误子载波的方法，并通过仿真得到近似BER。仿真结果表明，在高信噪比（SNR,signal to noise ratio）时，所提出的UTM 信道交织器能实现比随机交织器更低的系统BER。

1 基于BICM-OFDM 的UTM 通信系统

本节首先介绍了基于夹芯板式压电换能器（SPPT,sandwiched plate piezoelectric transformer）的UTM 信道及其特点，然后分别介绍了UTM 通信系统的发射端和接收端的数据处理过程。

1.1 基于SPPT 的UTM 信道及其特点

如图1 所示，UTM 信道一般由金属墙、耦合层、同轴固定于金属墙两侧的压电换能器和两侧的宽带匹配滤波器组成，其中，宽带匹配滤波器用于UTM 信道的阻抗匹配，以降低传输过程中的功率损失。超声波由发射端换能器产生，穿透各层传播后到达接收端换能器。由于超声波在不同介质的分界面会发生折射和反射，因此仅有一部分超声波到达接收端，另一部分超声波则被反射回发射端，再由发射端反射回来，如此往复进行，导致接收端收到多个超声波信号，这种回波现象类似于无线通信中的多径效应，使UTM 信道具有频率选择性衰落。

图1 UTM 信道的一般结构

本文采用的是基于SPPT 的UTM 信道分析模型[24]，图2 给出了63.5 mm 金属厚度的UTM 信道功率增益曲线与频率的关系，其中频率表示压电换能器的驱动电压频率。

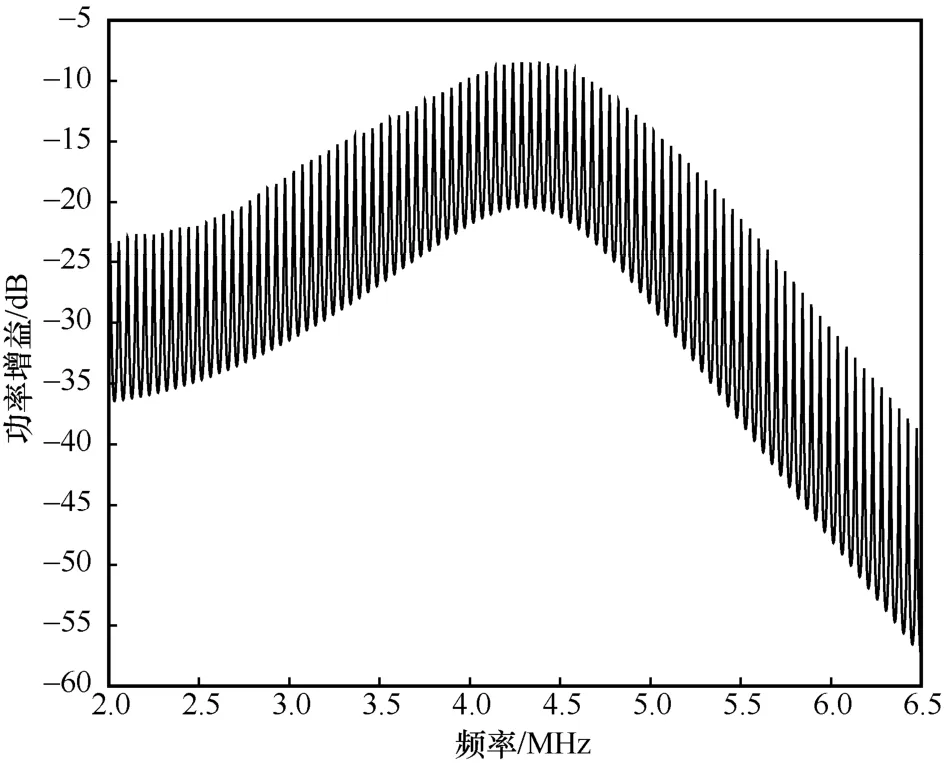
图2 63.5 mm 金属厚度的UTM 信道功率增益曲线与频率的关系

从图2 可以看出，UTM 信道的整体功率增益较低，大部分都小于-15 dB，且UTM 信道的功率增益在整体上具有起伏变化的特点，靠近换能器中心频率（约4.28 MHz）处的功率增益较高（-10 dB），远离换能器中心频率处的信道功率增益逐渐降低，在2 MHz 处约为-30 dB，在6 MHz 处约为-40 dB。同时，UTM 信道功率增益还有周期性的振荡变化，一个周期内的功率增益变化可达10 dB，这意味着UTM 信道具有严重的频率选择性。由于UTM 信道功率增益曲线的振荡周期是有规律的，因此可以通过式(1)[9]计算得出。

其中，ds为金属厚度，cs=5 838m/s 为超声波在金属中的传播速度。从式(1)可以看出，金属厚度越大，功率增益曲线的振荡周期越小。根据式(1)可以计算出图2 的功率增益曲线振荡周期约为46 kHz，UTM信道的频率选择衰落较严重，因此，必须采用较小的OFDM 子载波间隔。而较小的子载波频率间隔会导致OFDM 系统对相位噪声和同步误差过于敏感，所以，超声波透金属通信的相关研究所考虑的金属厚度一般仅有几十毫米。

UTM 信道一旦建立，在短时间内就不会发生明显的变化。一般来讲，由锆钛酸铅材料制成的压电换能器的压电效应随着温度的升高而逐渐减弱甚至消失。然而，温度的变化是较缓慢的，可能由昼夜交替、四季变化、地理位置的改变而引起，因此，一般将UTM 信道视为准静态信道[1]。UTM 信道是一种恒参信道，振荡周期、回波衰减的幅度几乎不随时间变化，其他典型的恒参信道包括一般的有线信道以及卫星通信信道等。

由于UTM 信道中收发端换能器相对固定，不存在相对运动，并且由声速变化引起的多普勒频移可忽略，因此，可以认为超声波透金属信道中不存在多普勒频移。

1.2 UTM 通信系统的发射端

由于UTM 信道是准静态的，容易满足信道相干时间大于多个OFDM 符号时间，保证了UTM 信道在多个OFDM 符号持续时间内不发生变化，因此，以下省略OFDM 符号的时间序列，仅考虑单个OFDM 符号。

图3 为基于BICM-OFDM 的UTM 通信系统结构。在发射端，比特流输入被分组表示，设比特流输入序列经过码率为rc的编码器（ENC）后得到长度为N的编码比特序列。然后，c经过交织器（Π）得到交织序列经过映射器（Φ）被分组映射到星座图上得到调制符号。

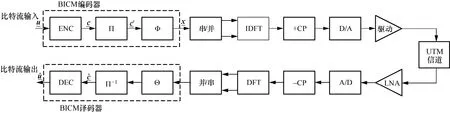
图3 基于BICM-OFDM 的UTM 通信系统结构

由于QAM 符号可以被分解为同相与正交2 个统计独立的脉冲振幅调制（PAM,pulse amplitude modulation）符号，为了简化分析且不失一般性，本文仅考虑PAM。

设星座图中的PAM 符号有M个，PAM 符号经过归一化处理后的平均功率为ES，单个PAM 符号为m=lbMbit。设经过映射得到的PAM 符号序列为，其中，X 为所有PAM 星座点的集合，为一个码字的PAM 符号个数。考虑到信道估计要使用部分子载波作为导频，仅有一部分OFDM 子载波可以传输数据，因此，如果设置K等于传输数据的子载波数，则解码操作可以在一个OFDM 符号内完成，避免了额外的时延。

从分集的角度看，在具有频率选择性衰落的信道中，交织器最重要的作用是实现频率分集。同时，由于UTM 信道的准静态特性，在时域上的交织并不会提高分集增益，因此，本文仅考虑单个OFDM符号内的交织。设 Nc=｛1,2,…,N｝表示编码比特序数的集合，Nb=｛1,2,…,m｝表示一个PAM 符号中比特位置的集合，Ns=｛1,2,…,K｝表示OFDM 中子载波序数的集合，则交织器可表示为

其中，nb∈Nc表示第nb个编码比特，ks∈Ns表示OFDM 符号的第ks个子载波，ip∈Nb表示PAM 符号的第ip个比特位置。

1.3 UTM 通信系统的接收端

本文假设UTM 信道的收发端具有完美的定时同步。在接收端，接收信号首先经过低噪放大器（LNA,low noise amplifier）和模数转换（A/D）得到数字信号。然后，接收端从收到的数据中移除CP（-CP）并进行DFT 后，得到各子载波信号为

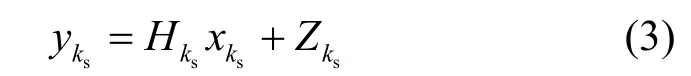
其中，Hks表示信道频率响应，表示Zks服从均值为0、方差为N0的加性复高斯白噪声。符号信噪比定义为子载波符号平均功率ES和噪声平均功率N0的比；子载波瞬时信噪比定义为带有子载波信道增益的信噪比，即和N0的比；另外，还有比特信噪比。当每个符号的比特数相同，且编码码率相同时，符号信噪比与比特信噪比具有一一对应的关系。本文所说的信噪比可以理解为符号信噪比，或与之对应的比特信噪比。

信号yks先经过并串变换（并/串）后，再由解映射（Θ）计算出第ks个符号第ip个比特的对数似然比（LLR,log-likelihood ratio），然后，LLR 经过解交织（Π-1）和解码（DEC）得到估计比特。

为了降低LLR 的计算量，一般采用最大对数近似法[25]，得到近似的LLR 为

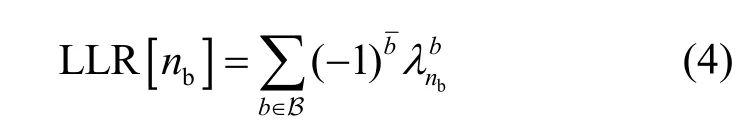
其中，nb=Π-1(ks,ip)，b表示取补，为第nb个比特的比特度量，如式(5)所示。

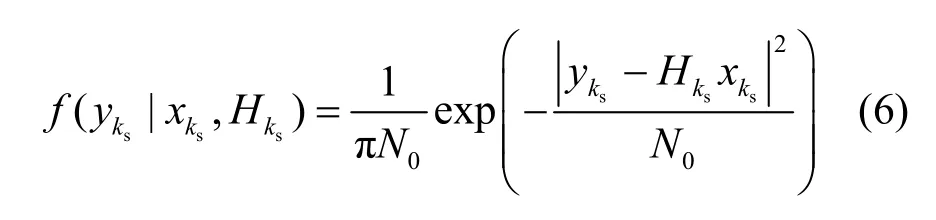
2 UTM 信道交织器的设计

本节首先介绍了高阶调制的UEP 和多输入交织器，然后根据UTM 信道特点设计了UTM 信道交织器，并给出了UTM 信道交织器中各个子交织器的实现方式，最后简要分析了UTM 信道交织器的复杂度。

2.1 UEP 和多输入交织器

图4 为采用二进制反射格雷码（BRGC,binary reflected Gray code）的8PAM星座图。BRGC是BICM中常用的一种映射方式，其重要性是在高SNR 时使比特错误概率最小。定义PAM 星座点的最左侧比特为最高位比特，比特位置为1，最右侧比特为最低位比特，比特位置为m。高阶调制会使不同的比特位置受到不同程度的噪声干扰，这种情况被称为UEP。例如，在图4 中，当符号x2受到噪声干扰被判为相邻符号x1或x3时，除了最高位比特是正确的外，其余位置的比特均会发生错误。

图4 采用BRGC 的8PAM 星座图

当系统采用高阶调制时，交织器的设计必须要考虑到UEP。文献[16]提出了使用m个子交织器对不同比特位置的比特进行交织的方法，即多输入交织器，如图5 所示。多输入交织器的特点在于，具有相同比特位置的比特处于同一个子交织器，这样能够保证交织前后的比特位置没有发生改变，避免出现在交织比特序列中某一段比特具有相同比特位置进而产生连续错误比特的情况，这在一定程度上降低了UEP的影响。

图5 多输入交织器的结构

从1.1 节的分析可知，UTM 信道的功率增益变化具有一定的周期性。即使采用多输入交织器对输入比特按比特位置进行分组，同一组的比特错误概率仍然具有较高的振荡性。虽然这样的高振荡会带来错误的不均匀分布，但是这种高振荡具有一定的规律，因此，可以利用这种振荡来设计多输入交织器。

2.2 UTM 信道交织器

首先，定义一些与UTM 信道有关的参数。定义UTM 信道功率增益曲线的一个振荡周期中包含的OFDM 子载波数为

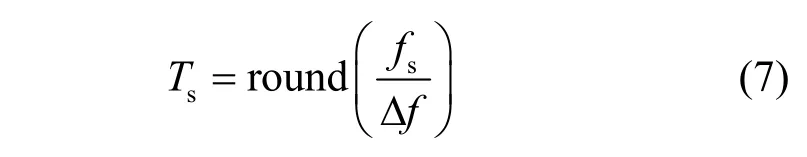
按照Ts（或Tb）可将一个OFDM 符号的所有子载波（或所有比特）划分为个组。定义Ti,j为第i个组的第j个比特，其中，｛1,2,…,G｝，j∈ Tb= ｛1,2,…,Tb｝。定义同一组的不同位置的比特集合为

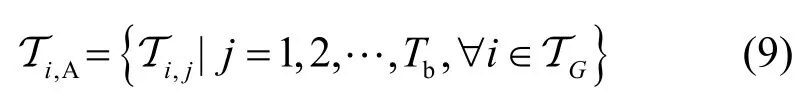
同时，定义不同组的相同位置的比特集合为

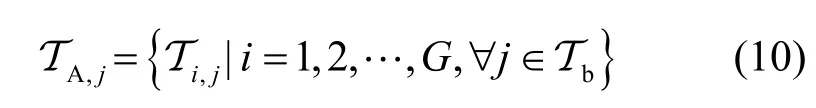
其中，A 表示取该序数的所有可能值。需要注意，式(9)和式(10)为编码比特数N被Tb整除的情况。若NmodTb＞ 0，可能出现的情况。

将一个OFDM 符号的所有子载波划分为G个组，每个组内的子载波大概处于UTM 信道不同周期的相同位置，与整个UTM 信道的功率增益振荡相比，每个组内的子载波所经历的振荡更加平缓。如果采用多输入交织器的思想对每组中同一比特位置的比特进行交织，即对 TA,j进行交织，那么，不仅可以使 TA,j在整体起伏的UTM 信道上交织，保证了同一组比特在交织后落在不同的振荡周期中，而且没有打乱比特位置，降低了UEP 的影响。

令图5 中的交织器个数为Tb，即可得到UTM 信道交织器，图6 给出另一种更形象的表示方法，其中矩阵的元素为输入比特的比特位置。首先，输入比特按列写入Tb行G列的矩形存储器；然后，多输入交织器分别对矩形存储器中每行的所有比特（例如，图6 中所圈出的第一行比特）进行交织；最后，按列读取矩形存储器的所有比特。一般情况下，由于比特数N不能被Tb整除，交织时可忽略第G列包含的TbG-N个空元素。从图6 也可以看出，交织后的比特位置不会发生变化。

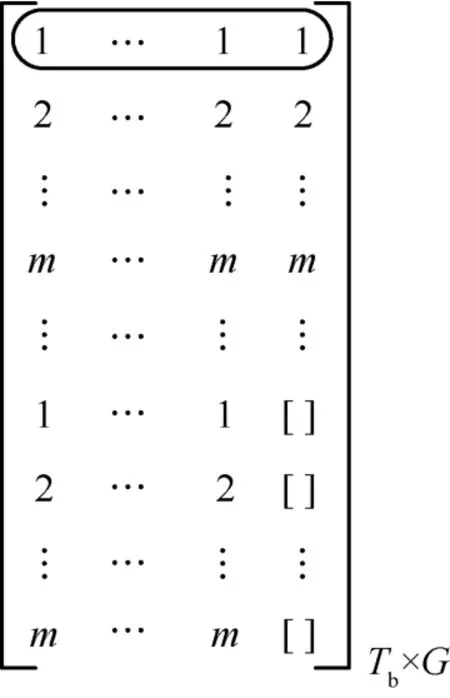
图6 UTM 信道多输入交织器的矩形存储结构

接下来，分析声速对UTM 信道交织器的影响。在金属厚度和子载波间隔不变的条件下，声速会影响Ts的大小，进而影响UTM 信道交织器的结构。一般情况下，在实际系统中使用的声速参数不会过于偏离真实声速，可以认为Ts在 ±1 范围内变化，这种变化可能会略微加剧子载波分组的误差，使同组比特所经历的功率增益振荡更大，进而影响所提交织器的性能。然而，由于声速变化是缓慢进行的，可以在信道估计过程中较准确地得出，因此，对子载波分组的误差主要来自Ts的四舍五入。

2.3 最小跨度与单个交织器的设计

有效的信道交织器必须能充分利用OFDM 多载波技术的时间和频率多样性，因此，从分集的角度看，信道交织器的一个重要设计参数是跨度特性。最小跨度是一个常用的衡量比特分离程度的参数，在设计信道交织器时，为了降低交织比特的相关性，必须最大化交织器的最小跨度。

描述最小跨度的常用方式有L1 度量（即曼哈顿度量）和Lee 度量[26]，其中，Lee 度量是一种周期性的度量方式，对距离取模计算，如式(11)所示。

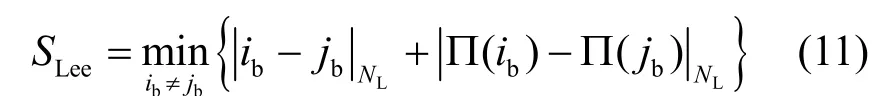
其中，ib,jb∈Nc，NL为Lee 度量的周期，|ib-jb|NL为Lee 度量下ib和jb的距离，由式(12)给出。

文献[27]表明，Lee 度量下最小跨度的上界为

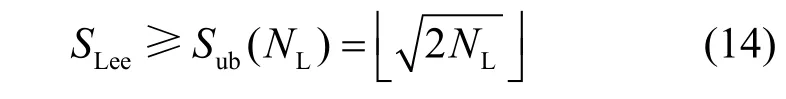
式(14)也可以理解为NL长的比特序列经过交织后能得到的最小Lee 度量距离为Sub(NL)。

矩形交织器是一种简单且常用的比特级交织器，输入比特按列依次存储到矩形存储器，输出端按行依次读取输出比特。矩形交织器[25]可表示为

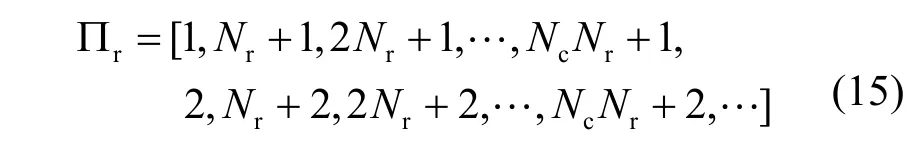
其中，Nr为矩形交织器行数（即交织深度），为矩形交织器列数。通过选择矩形交织器的交织深度（如式(16)所示），可以最大化Lee度量下的最小跨度。

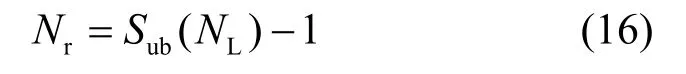
2.2 节所设计的UTM 信道多输入交织器已经将周期变化的比特分散到各个子交织器中，每一个子交织器所包含的比特所经历的信道功率增益变得平缓。因此，各个子交织器只需要按式(16)采用矩形交织器，即可将子交织器的比特进一步打散。

如果所有子交织器采用相同的矩形交织，相当于对图6 的列进行了整体的移位，这样并没有打散同一列的相邻比特。为了避免这种情况，可以在交织前对每一个子交织器的所有比特进行不同的行循环移位。一种简单的方式是第j行向后循环移位j-1位后再进行子交织。

2.4 UTM 信道交织器的复杂度分析

实现UTM 信道交织器的主要步骤如下。

1) 将一个OFDM 符号的N个编码比特按列写入Tb行G列的矩形存储器，第G列的比特数可能小于Tb。

2) 对第j行循环移位j-1位。

3) 对循环移位后的每组比特进行Sub(G) -1的矩形交织。

4) 按列读出交织比特序列。

与一般的矩形交织器相比，UTM 信道交织器额外包含了循环移位与矩形交织的步骤，其中，矩形交织实际上是比特的存储与读取，存储可以从每组比特的任意位置开始，因此，可以省去循环移位这一步操作。假设每个比特的存储或读取需要花费一个时钟周期，那么所提UTM 信道交织器的时间复杂度为O(4N)。如果采用并行的方式对每组比特做矩形交织，那么只需要花费一次矩形交织的时间，所提 UTM 信道交织器的时间复杂度为O(2N+G)。因此，所提UTM 信道交织器的复杂度很低，在实际中可以轻松地实现。

3 UTM 信道交织器的性能分析

本节采用文献[20]的分析方法对基于BICMOFDM 的UTM 通信系统比特错误概率Pb进行分析，并采用随机选择的方法得到错误信道系数。

3.1 卷积编码的下界

对于卷积编码，虽然联合界可以作为Pb的上界，但是必须考虑所有大于或等于最小自由距df的错误路径，计算较复杂，因此，可以通过仅考虑自由距为df的错误路径，对高SNR 情况下的比特错误概率进行简化，如式(17)[20]所示。

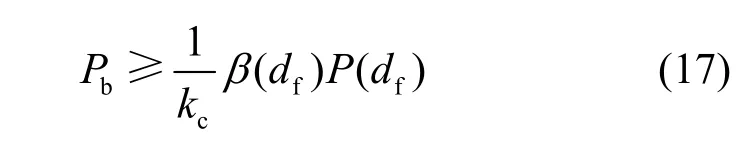
其中，kc表示卷积编码器中输入的每组信息比特个数；β(df)表示汉明距为df的错误路径输入权重，文献[28]给出了β(df)的详细数据，可通过查表法得到；P(df)表示汉明距为df时码字的成对错误概率（PEP,pairwise error probability）。式(17)的值主要取决于P(df)，当SNR 增加时，汉明距为df的错误路径逐渐成为主要错误形式，式(17)逐渐变得紧致。

假设df个错误比特分别映射到不同的PAM 符号中，在高SNR 的条件下，条件PEP 为[20]

其中，Q(·)表示Q函数，kω表示第ω个错误比特处的 第kω个 PAM 符号，和分别表示df个错误比特所在的PAM符号向量和比特位置向量，表示信道系数向量，表示估计码字向量，表示独立同分布的随机变量，其中

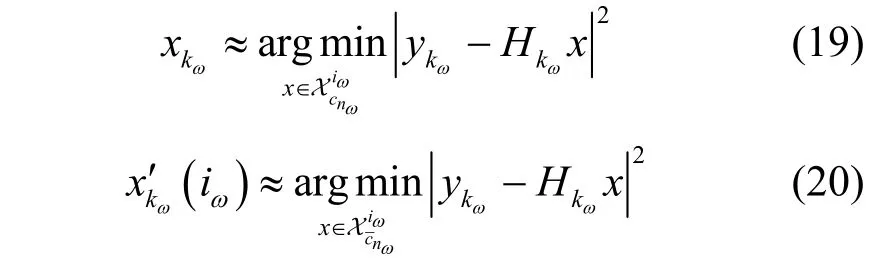
将式(18)中的求和项单独写出，即

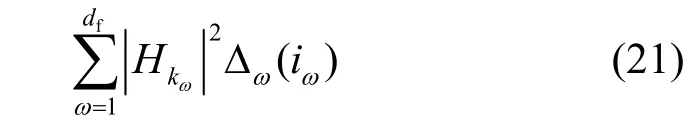
文献[20,29]对式(21)进行奇异值分解，然后利用随机信道的幅值期望，计算出条件PEP。同时，文献[20]通过仅考虑 Δω(iω)的最小项，给出了加性白高斯噪声信道下的简化PEP 表达式。

3.2 随机交织器的性能

随机交织器需要额外的随机数存储空间并且严重依赖于伪随机数生成器，难以在实际中应用，一般将其作为对照组进行分析。随机交织器将错误比特随机且均匀地分散到不同的PAM 符号中，这使任意df个不同的PAM 符号都可能产生错误路径。同时，考虑到符号错误概率受子载波瞬时信噪比的影响，因此，准确计算df个Hkω的概率分布公式是比较困难的，同时也难以遍历所有种情况。

为了简化上述问题，本节采用随机选择的方法计算式(21)的值。当随机选择的df个子载波具有较高的功率增益时，由于式(21)的值与成正比，得到的条件PEP 值会很低；相反，当随机选择的df个子载波具有较低的功率增益时，条件PEP 值会很高。这种随机选择的方法不需要遍历df个错误子载波的所有情况，大大降低了计算量。

对于 Δω(iω)，也可以采用随机选择的方法，以下给出随机交织器中 Δω(iω)的概率质量函数。在随机交织器中，iω可视作均匀分布，而 Δω(iω)的分布仅与iω有关，因此，Δω(iω)的概率分布可通过遍历所有的符号对，再求和取平均得到，即

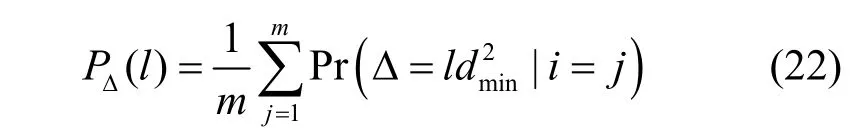
其中，dmin为星座图的最小欧氏距离。例如，当采用4 PAM 时，式(22)为

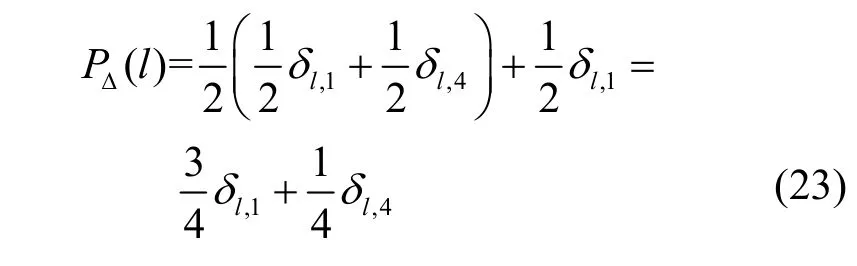
其中，δa,b表示Kronecker 符号函数。

3.3 UTM 信道交织器的性能

第2 节所提出的UTM 信道交织器具有规则的比特位置排列，因此，求解 Δω(iω)并不复杂，但是，计算df个的概率分布依然很复杂。

当最小自由距离df=5时，仅有一种错误形式且错误路径仅在处开始产生，因此，当给定M时，可能会得到不同的例如，当m=4时，有2 种情况，即

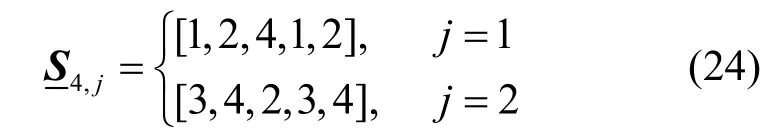
虽然可以计算出每个编码比特的错误概率，但是由于这些错误概率并不是相互独立的，比如同一个PAM 符号的几个比特错误概率并不独立，并且还需要根据去遍历整个编码比特，因此，将比特错误概率和df个Hkω的概率联系起来也较困难。

考虑采用与3.2 节相同的随机选择方法。对于UTM 信道交织器，低功率增益子载波所产生的错误比特被较均匀地分散到整个编码比特中，这些错误比特不会产生错误路径，进而可以被译码所纠正，因此，在计算近似BER 时，就需要排除这些错误比特所在的子载波，在剩下的子载波中选择df个错误子载波，即可得到UTM 信道交织器的近似误比特率。当然，如果忽略的低功率增益的子载波个数太大，近似BER 会偏低；反之，近似BER 会偏高。

4 UTM 信道交织器的仿真分析

本节对UTM 通信系统进行了仿真分析，首先给出了仿真参数的设置，然后分别对加性白高斯噪声所产生的随机错误和不同金属厚度进行了仿真，最后讨论了解交织比特序列的错误概率变化情况。

4.1 仿真参数

UTM 通信系统的部分仿真参数如表1 所示。编码器采用约束长度为3 的 (7,5)8卷积码，译码器采用维特比软译码。映射方式采用BRGC。对每个SNR 进行蒙特卡罗仿真，比特数均超过 107个。本文不考虑信道估计方法，假设接收端已知信道状态信息。虽然假设了接收端已知信道状态信息，但为了与实际相符，仍考虑采用导频，此时数据子载波的个数降低，同时Ts也降低。本节仿真的交织器包括本文提出的UTM 信道交织器、随机交织器以及无交织器。

表1 UTM 通信系统部分仿真参数

4.2 UTM 通信的BER

图7 绘制了采用4PAM 和16PAM 的不同交织器BER 与的关系，采用的交织器包括随机交织器、UTM 信道交织器和无交织器的情况。从图7可以看出，随着SNR 的增加，UTM 信道交织器的BER 逐渐优于随机交织器的BER，且两者差距逐渐加大，这说明所提交织器在UTM 信道中能提供更高的分集增益。在高SNR 时，随机交织器和UTM信道交织器的近似BER 和仿真BER 吻合较好，因此，可以得出结论，即第3 节的随机选择方法能实现对高SNR 时仿真BER 曲线的有效近似。仿真的UTM 信道交织器所忽略的低功率增益子载波的个数为300 个，这是本节仿真所采用的经验值数据。

图7 采用4PAM 和16PAM 的不同交织器的BER 与的关系

4.3 不同金属厚度的仿真

图8 绘制了在SNR=45 dB 和16PAM 时UTM 通信系统的BER 和金属厚度的关系。从图8 可以看出，除了UTM 信道交织器外，其他交织器在不同金属厚度时的BER（包括仿真BER 和近似BER）基本保持稳定。虽然信道状态随着金属厚度的变化而变化，使UTM 信道交织器的近似BER 难以对实际BER 进行预测，但是依然可以通过仿真BER 来评估所提交织器的性能。随着金属厚度的增加，UTM 信道交织器的仿真BER 逐渐升高，这是因为UTM 信道功率增益曲线的振荡周期变小，使一行的比特（TA,j或图6 的一行）所处的子载波位于不同周期的不同位置，换句话说，虽然按振荡周期对编码比特进行了分组，但是由于式(7)的截断误差，同一行的比特仍在经历起伏的信道功率增益变化，因此，本文所提的UTM 信道交织器会受金属厚度的影响。

图8 在SNR=45 dB 和16PAM 时UTM 通信系统的BER和金属厚度的关系

4.4 UTM 通信中解交织比特序列的错误概率

图9 绘制了在4PAM 和SNR=40 dB 时所提交织器的解交织比特序列的错误概率，其中，图9(a)绘制了全部解交织比特序列的错误概率，图9(b)绘制了部分解交织比特序列的错误概率。从图9可以看出，UTM 信道交织器将高错误概率的比特较均匀地分散到了整个编码比特中，例如，图9(a)中Pb＞0.4 的部分比特，这些高错误概率比特的两边是错误概率较低甚至接近0 的比特（如图9(b)所示），所以产生连续错误比特的概率较低，可以在卷积译码中被纠正，进而降低了UTM 系统的BER。

作为对比，图10 绘制了在4PAM 和SNR=40 dB时随机交织器的解交织比特序列的错误概率。从图10可以看出，采用随机交织器的解交织比特序列错误概率非常均匀，虽然单个比特发生错误的概率较低，但是，由于在连续的几个比特中每一个比特都有一定的错误概率（约0.05），因此，与所提交织器相比（如图9(b)所示），随机交织器产生连续错误的概率更大，进而系统BER 更大。

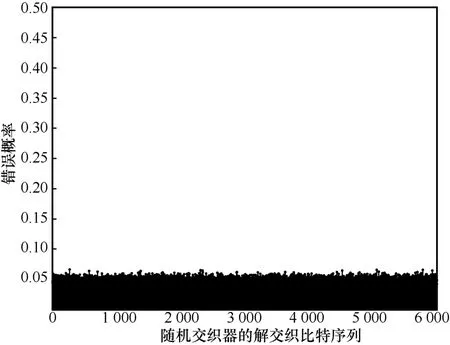
图10 在4PAM 和SNR=40 dB 时随机交织器的解交织比特序列的错误概率

5 结束语

本文提出了一种UTM 通信多输入信道交织器，主要利用了多输入交织器的分组思想，将编码比特按照UTM 信道功率增益的周期振荡特性进行分组，使每组比特的错误概率变化更加平缓，不仅降低了高阶调制中UEP 的影响，而且将UTM 信道中一个振荡周期内的连续错误比特分散到了不同的振荡周期中。所提信道交织器的实现也很简单，仅需要少量的存储与读取操作。此外，本文也对随机交织器和所提信道交织器的性能进行了分析，虽然比特错误概率的解析解难以得到，但是通过随机选择的方法可以得到近似的BER。

仿真结果表明，在高SNR 时，所提信道交织器在不同调制方式时均能实现比随机交织器更低的系统BER。当SNR 较低时，受限于编码器的纠错能力，所提信道交织器与随机交织器的BER 性能接近，采用更先进的编码技术可以降低BER，但是编码复杂度也会有所提升。本文还仿真了不同金属厚度对所提信道交织器的影响，结果表明，当金属厚度较大时，由于周期取整产生的截断误差，同一个子交织器中的比特仍在经历起伏的信道功率增益变化，这使所提信道交织器的系统BER 随金属厚度增加而逐渐提高。最后，给出了采用所提信道交织器和随机交织器的解交织比特序列的错误概率，可以看出，高错误概率的比特较均匀地分散到了整个编码比特，进一步验证了所提信道交织器的有效性。