基于深度强化学习的海洋移动边缘计算卸载方法
苏新,孟蕾蕾,周一青,CELIMUGE Wu
(1.河海大学物联网工程学院,江苏 常州 231022;2.中国科学院计算技术研究所处理器芯片全国重点实验室,北京 100190;3.中国科学院大学计算机科学与技术学院,北京 100190;4.日本电气通信大学信息理工学,东京 182-8585)
0 引言
国家“十四五”规划明确提出要积极拓展海洋经济发展空间,协同推进海洋生态保护、海洋经济发展和海洋权益维护,加快海洋强国建设。当前,国家正在加大开发利用海洋多样化数字资源的基础建设投入,构建具有自主核心技术的下一代海洋信息系统,围绕海洋工程、资源、环境等领域攻克一批技术难题,突破海洋霸权强国的封锁,使我国全天候、全自动的海洋观监测活动稳扎深蓝远海[1]。
移动边缘计算作为5G 关键技术之一,将其应用于下一代海洋信息系统有望提供各类海洋感知数据的实时处理能力,满足高可靠、低时延海事应用的快速响应需求[2-3]。研究表明,基于移动边缘计算的海洋信息实时处理性能相比传统方式可以极大提高处理效率[4]。面向下一代海洋信息系统建设,该技术具有极高的研究意义和应用价值。
计算任务的有效卸载作为移动边缘计算的核心功能,已在陆地蜂窝网和车联网等应用场景下展开了深入研究和广泛应用[5-6]。然而,与传统陆地移动边缘计算任务卸载不同,制定海洋环境下的计算任务卸载策略将会面临全新的技术挑战。
1) 海洋网络节点离散、分布不均,计算能力与能耗敏感度存在差异,海洋网络各节点之间的强异构特性为计算任务卸载优化带来了复杂高维度的限制条件。
2) 复杂多样化的海事应用会导致海洋网络局部区域出现计算任务的超负荷处理,实现海洋网络节点计算任务的最佳卸载与资源分配是保障海事应用服务性能的关键。
通过调研已有计算任务卸载方法,结合海洋环境下的计算任务卸载技术挑战,以满足高可靠、低时延的海事应用服务为目标,本文提出了基于深度强化学习的计算任务卸载方法,联合优化海洋网络节点卸载决策与资源分配,主要学术贡献包括以下几个方面。
1) 针对海洋节点强异构下的卸载问题,刻画全新海洋信息系统下的计算任务卸载场景,利用海洋网络节点的计算能力、传输能力、可分配存储能力等多种异构特征属性对海洋网络节点进行归类分层。
2) 提出面向下一代海洋信息系统的多节点卸载模型,以最小化海洋网络节点计算任务执行时延为目标,利用人工智能与凸优化等手段,联合优化海洋网络节点计算任务卸载决策与资源分配问题,提升系统服务性能。
1 相关工作
欧洲电信标准化协会于2016 年将移动边缘计算的概念扩展为多接入边缘计算(MEC,multi-access edge computing),并扩大了其研究范围,包括LTE、固定宽带和Wi-Fi 技术的异构组网模式[7]。MEC 技术优势主要体现在超低时延、高带宽、高可靠性以及可扩展性等方面,可以辅助运营商灵活快速地向移动用户和企业部署新的服务。MEC 可利用计算任务卸载实现系统分布式计算框架下的边缘计算节点负载均衡,通过适配网络节点计算能力和与其对应的数据负载,实现边缘计算节点的同步处理,获取最短的应用服务时延。
面向陆地蜂窝网络,MEC 可以通过计算任务的卸载大幅降低网络的回程流量、传输成本和数据泄露风险。文献[8]研究了单服务器场景下的多用户计算卸载问题,通过一种基于软件定义网络的Stackelberg 博弈模型,实现了任务最佳卸载。但是,文献[8]中模型计算复杂度高,不适用于任务实时卸载的相关应用场景。文献[9]面向任务实时卸载应用场景,将卸载问题转化为二阶锥规划问题,并利用一种基于逐次凸逼近的算法进行迭代求解,降低了求解方法的复杂度。然而,文献[9]尚未考虑边缘计算节点的动态移动性,导致其适用性较弱。文献[10]研究了MEC 系统中时延和能耗之间的基本权衡,提出了一种基于迭代启发式的在线卸载算法,获得了较好的服务性能。文献[11]将计算卸载决策表示为有限时间的马尔可夫决策过程,并采用动态规划方法求解最优卸载决策,实现了最小化系统时延的目标。然而,文献[11]未考虑能耗约束会导致用户能耗过高。为同时满足用户对时延与能耗的要求,文献[12]针对蜂窝网络中边缘网络与中心云计算之间的协同卸载问题,提出了一种基于分解法和连续伪凸法的框架,并通过迭代算法降低了系统成本。
面向车联网等时延敏感型应用,MEC 技术优势主要体现在降低网络时延、提高用户的体验质量。文献[13]设计了一种基于预测卸载的传输机制,将任务提前传输至MEC 服务器,一旦车辆进入服务器覆盖范围便可立即响应,实现了降低车辆计算任务执行时延的目标。但是,文献[13]忽略了节点负载均衡,导致部分服务器由于过载而限制其性能的提升。文献[14]则将负载均衡与卸载相结合,研究了多用户多服务器系统的资源分配问题,提升了系统性能。然而,文献[14]假设车辆匀速移动,不符合实际车联网的应用场景。针对车辆移动性问题,文献[15]研究了车辆随机移动场景下的MEC 系统性能,提出了相应的移动感知卸载机制,降低了系统运维成本。但文献[15]采用了单跳的任务卸载方式,导致其系统模型对环境的适应性较弱。在此基础上,文献[16]研究了针对多跳车辆场景的有效联合卸载,并制定了双端优化问题,联合优化了用户端和服务端的服务成本。但是,文献[16]仅考虑了正交多址应用场景下的车载MEC 系统,导致其系统模型过于单一。文献[17]进一步考虑了正交多址和非正交多址2 种应用场景下的车载MEC 系统,提出了基于启发式算法的任务卸载机制,获得了系统最小化任务总执行时延。
移动边缘计算卸载场景实际上存在动态、随机、时变等特性,而上述面向陆地蜂窝网和车联网的任务卸载方案的主要目的是得到更好的卸载决策,缺乏对实际场景下决策算法高实时性要求的考虑。随着人工智能技术的兴起,研究者逐步将其与移动边缘计算技术进行有效结合,可以更好地解决动态、随机、时变环境下的计算任务卸载优化问题。
文献[18]研究了车联网中的任务卸载和资源分配问题,并提出了一种基于Q-Learning 的任务卸载和资源分配算法,但是文献[18]仅考虑了单一的MEC 系统。文献[19]针对蜂窝网中的多个MEC 系统,提出了一种基于Q-Learning 的联合通信和计算资源分配机制,优化了满足能量约束条件下的任务处理时延,并通过仿真实验验证了所提方法具有较好的环境适应性。文献[20]面向动态卸载场景,利用一种基于软件定义网络(SDN,software defined network)边缘云的新型Q-Learning 优化框架制定卸载决策和资源分配,能够快速适应梯度更新和样本数量较少的全新通信环境。虽然文献[18-20]利用Q-Learning 方法在特定场景下达到了较好的卸载效果,但是当优化问题的状态和动作空间过大且高维连续时,存储Q值的内存空间将呈指数级增长,在搜寻最优卸载决策时也会产生大量的时间开销。为此,研究者利用深度学习技术解决了传统强化学习存在状态空间中的高维问题。文献[21]考虑了一个包括陆基、车辆以及无人机的混合移动边缘计算平台,以最小化终端设备能耗为目标,提出了一种基于深度学习的混合在线卸载算法框架,但是每次仅限输入一个设备信息,不适用于实际应用场景。文献[22]研究了车辆-车辆(V2V,vehicle to vehicle)与车辆-基础设施(V2I,vehicle to infrastructure)之间的联合卸载问题,提出了一种多智能体深度强化学习框架,达到了同时满足V2I 和V2V 链路时延要求的目标,但是该方法收敛速度较慢。文献[23]考虑了多用户和多服务器的MEC 场景中的任务卸载决策问题,提出了一种基于深度强化学习的在线卸载算法,解决了计算任务卸载时长的优化问题。
本文聚焦下一代海洋信息系统,面向多种海事应用并行、海洋网络拓扑较大且快变等特性,提出基于深度强化学习的海洋移动边缘计算卸载方法。截至目前,研究者针对海洋移动边缘计算已经提出了若干计算任务卸载算法,在一定程度上满足了海洋网络低时延高可靠的应用服务需求。
文献[24]分析了海洋通信时延和能耗之间的折中关系,提出了一种阶段性联合优化算法,在能量有限与时延敏感条件下优化了计算与通信资源的分配机制。文献[25]提出了一种基于海洋网络连通概率的边缘计算节点选取方法,根据海洋近岸和远岸的网络节点密度差异,建立了基于近海和远海场景的任务卸载模型,并分别利用遗传算法和粒子群优化算法进行求解。文献[26]利用混合整数非线性规划分离优化目标,有效地分配传输功率并通过改进传统人工鱼群算法制定了卸载决策。然而,上述文献均未充分考虑海洋网络节点之间的强异构特性。同时,启发式算法不仅在寻优时需要大量迭代,而且面对复杂卸载环境时算法计算能力会大幅下降,求解质量不能得到很好的保证。
表1 通过应用场景、系统模型、卸载算法、节点异构性、实现效率、适用规模等方面对上述文献进行了对比与总结。由表1 可知,传统MEC 卸载算法[8-17,24-26]计算复杂度较高,实现效率始终低于人工智能算法。基于强化学习的人工智能卸载算法[18-20]虽然能够达到较高的卸载效率,但存在维数灾难,只适用于小规模应用场景。基于深度强化学习的卸载算法[21-23]虽然能够克服维数灾难,但过于专注中心化的卸载策略,对新环境的适应性较弱。通过对比还可以发现目前针对海洋网络MEC 研究仍然存在以下缺陷:对综合考虑端-边协同架构中的计算任务卸载和资源分配问题的研究较少,并且已有文献尚未充分考虑海洋网络节点之间的强异构特性;没有对MEC 系统中的节点进行分层归类,在高维度时收敛速度慢,无法满足海洋监测网中低时延、高可靠的任务卸载需求,并且对快速变化的环境适应性较弱。
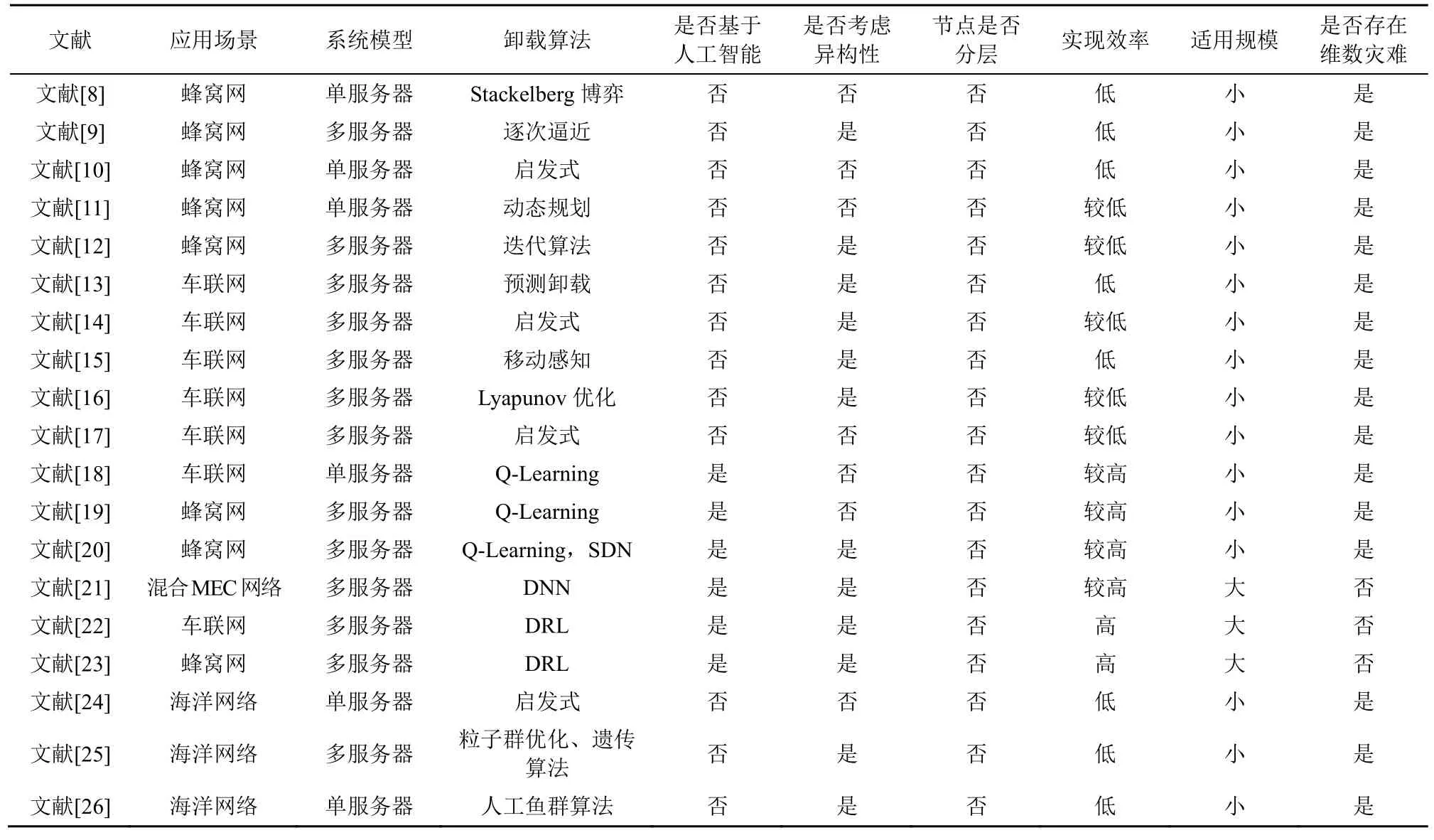
表1 MEC 卸载模型比较
2 海洋移动边缘计算任务卸载
2.1 海洋网络节点分层归类
图1 刻画了基于海洋网络的计算任务卸载模型。考虑到海洋网络节点的强异构特性,需要依据海洋网络节点特征属性对其进行归类分层,包括计算能力、可分配存储能力、传输能力、节点位置以及节点移动速率;并且可将节点归类划分为强型层、中型层、弱型层和独立层,分别用和表示,其中,m∈ {1,2,…,M},n∈{1,2,…,N},k∈ {1,2,…,K},o∈ {1,2,…,O}。具体分层归类策略如下。
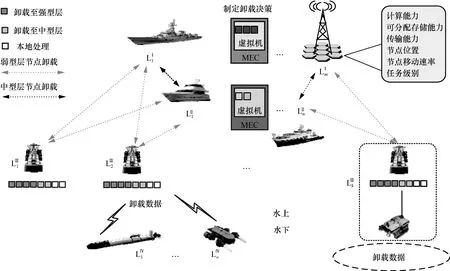
图1 基于海洋网络的计算任务卸载模型
强型层节点移动速率相对缓慢稳定,计算能力和可分配存储能力强、电量充沛,可有效快速地完成海量复杂的计算任务,主要由海岸基站和大型船舶等组成。中型层节点移动速率较快,计算能力和可分配存储能力较强,电量较充足,可处理复杂度一般的海事任务,主要由柴油驱动的中型船舶组成。弱型层节点计算能力和可分配存储能力弱,蓄电池电量受限,可处理普通的海事任务,主要由电力驱动的小型船舶以及海上浮标等组成。部分海上浮标可通过有线连接浅海区域水下机器人展开相关业务,因此将其视为一个节点整体。独立层节点主要位于水下,通过水声通信方式互联。若进行大规模的数据卸载,会产生较大时延,因此本文不考虑水下卸载过程,水下任务只在本地处理,该层节点独立于其他层的节点。

2.2 海洋移动边缘计算卸载时延模型



当网络中心节点根据卸载决策确定αI,αII,αIII、上行链路传输功率P以及相应的MEC服务器计算资源F时,执行完成所有节点的计算任务所需要的总时延为
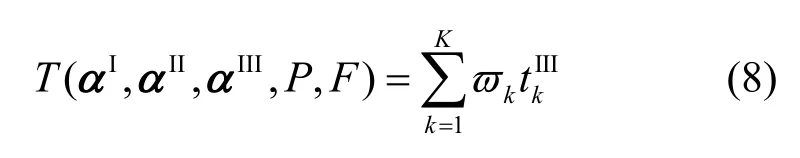
其中,ϖk∈ (0,1]为权重因子,用于指定资源提供者对节点的偏好,满足时延敏感性节点的需求[27],ϖk的值可以根据计算任务的关键性来设置。
2.3 海洋移动边缘计算卸载时延优化问题

式(9)的约束 C1表示任务执行方式为二进制卸载,约束 C2表示每个任务只能选择一种执行方式,约束C3和C4表示节点的传输范围限制,约束C5、C6、C7和 C8限定节点发送功率,约束 C9、C10、C11和 C12限定节点计算能力。
基于式(9)可知优化问题P1 是一个混合整数非线性规划问题[28-29]。面向多种海事应用并行、网络拓扑大而快变的海洋计算任务卸载场景,考虑海洋网络独有的节点强异构特性,优化问题P1 是一个大规模、高维度且具有诸多限制条件的复杂问题,即使能够描述出这种海洋移动边缘计算的卸载模型及问题,求解过程也会相当困难。为此,本文面向海洋移动边缘计算任务卸载,设计了一种基于凸优化-深度强化学习的计算任务卸载策略,从而避免解决使用传统方法难以求解的问题。
3 基于深度强化学习的计算任务卸载方法
优化问题P1 中P和F的最优值P*和F*是关于αI,αII,αIII的函数,因此问题P1 可以化简为
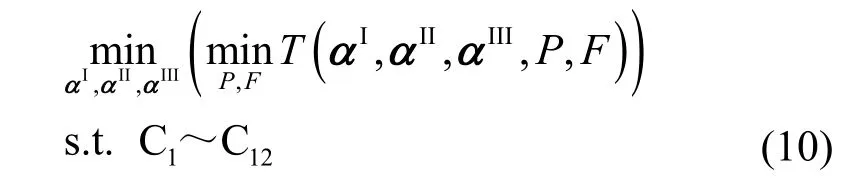
其中,约束 C1~ C4中的αI,αII,αIII与约束 C5~ C12中的P、F相互解耦。式(10)的求解等效于求解如下的主优化问题P2。
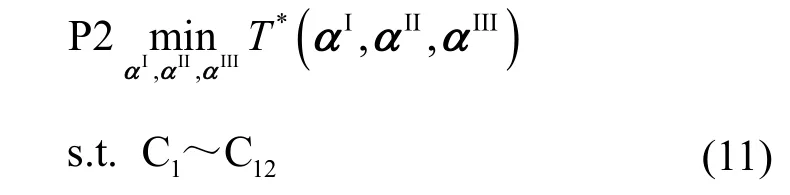
其中,T*(αI,αII,αIII)是对应P和F的最优解函数,具体表达式为
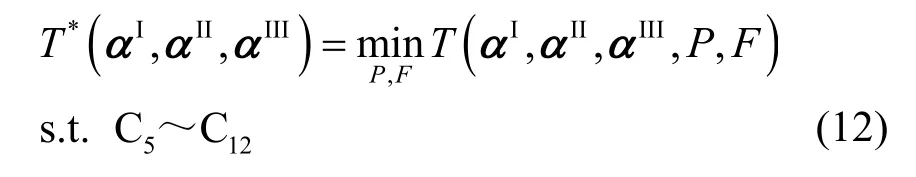
上述问题的分解不会改变原问题的最优解,同时式(12)具有变量可分离的结构,即P和F所对应的目标函数和约束彼此解耦。因此,式(12)可以分解为2 类子优化问题,其中,F*为子优化问题P3的最优解,P*为子优化问题P4 的最优解。本文针对任意卸载决策(αI,αII,αIII),利用相关算法推导出F*和P*的具体表达式。
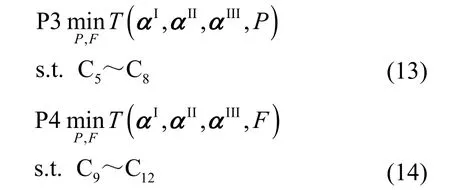
3.1 计算资源分配
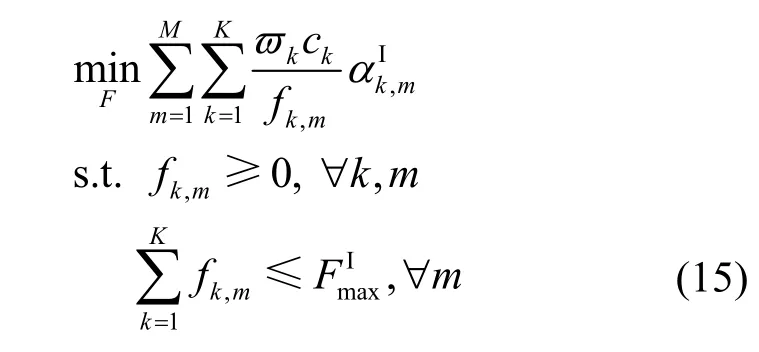
式(15)约束为凸,目标函数记为 Γ(αI,F),并且 Γ(αI,F)关于fk,m的二阶导数可以表示为

由此可知,式(15)为凸优化问题,可以使用KKT(Karush-Kuhn-Tucker)条件进行求解,其对应的拉格朗日函数可以表示为
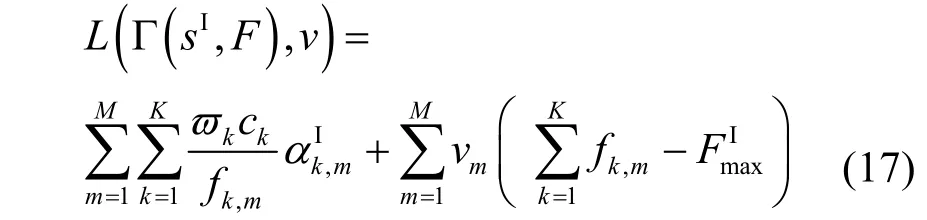
其中,v=[v1,… ,vM]为拉格朗日乘子。计算拉格朗日函数L(Γ(sI,F),v)关于fk,m的一阶导数为


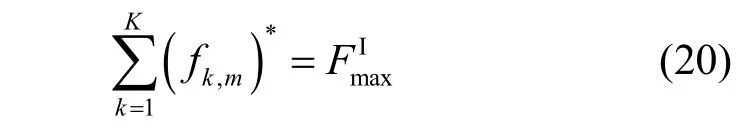
将式(18)代入式(19)可以得到拉格朗日乘子的具体表达式为

最后,将式(21)代入式(19),便可以得到式(15)的最优解为

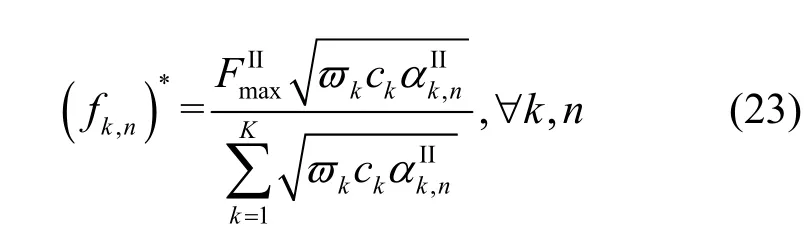
3.2 数据传输功率分配

3.3 卸载决策生成
当确定P3 和P4 的最优解后,将其代入式(12)可以得到T*(αI,αII,αIII)的具体表达式为

将式(27)代入式(11),进而主优化问题P2 可以更新为

通过分析可知式(28)为整数规划问题。由于传统算法求解整数规划问题存在维数灾难,本文针对上述优化问题提出一种基于深度强化学习并行计算在线卸载(OOPC-DRL,online offloading of parallel computing based on deep reinforcement learning)算法,可以规范高效地求解卸载策略,以最小化节点计算任务执行总时延。
OOPC-DRL 计算任务卸载策略架构如图2 所示,从图2 可知,OOPC-DRL 主要由生成卸载决策矩阵集、资源分配、生成最佳卸载决策矩阵和更新卸载经验4 个阶段交替完成。生成卸载决策矩阵集阶段主要依赖于并行的深度神经网络(DNN,deep neural network),DNN 根据当前时刻状态实时生成Ω个卸载决策矩阵,并且通过经验存储器在线学习定期更新参数。其中,当前时刻状态st包括海事应用任务数据量的大小Dk、节点的相关参数集合节点的相关参数集合,以及系统总带宽、信道增益和背景噪声功率。
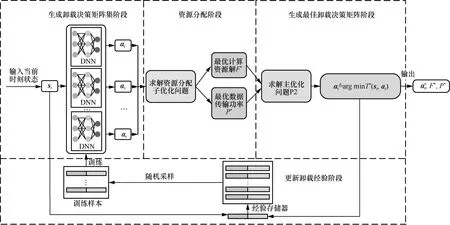
图2 OOPC-DRL 计算任务卸载策略架构
资源分配阶段将生成卸载决策矩阵集阶段所生成的决策矩阵分别代入子优化问题P3和P4求解其最优计算资源和数据传输功率,实现系统的最佳资源分配。生成最佳卸载决策矩阵阶段将前2 个阶段所产生的卸载决策矩阵集、最优计算资源和最优数据传输功率代入主优化问题P2,通过求解P2 生成最佳卸载决策矩阵。更新卸载经验阶段使用经验回放机制[30],将同一时刻的状态与最佳卸载决策矩阵合并作为卸载经验存储于经验存储器中,并在训练时随机采样作为训练样本。与使用整个数据样本集相比,OOPC-DRL算法降低了更新复杂度;通过降低训练样本之间的相关性,加快了网络收敛速度;重复使用历史数据,减少了迭代更新方差。此时,可以使用Adam 随机梯度下降优化算法更新DNN 中各网络参数[31],因此,平均交叉熵损失函数表示可以为

OOPC-DRL 算法具体表述如算法1 所示。
算法1OOPC-DRL 算法
输入神经网络参数θΩ,经验存储器B,当前状态st
输出卸载决策矩阵(αI,αII,αIII),计算资源F*,数据传输功率P*
初始化神经网络参数θΩ~N(0,1),经验存储器的大小
1) fort=1:T
2) 将当前时刻状态st进行归一化
3) DNN 根据归一化的st产生Ω个候选动作矩阵,并存入候选动作矩阵集C
4) 代入资源分配子优化问题最优解,即式(22)、式(23)、式(26),得出计算资源和数据传输功率最优解F*、P*
5)代入式(27)求解T*(st,αt)
8) if 经验存储器B的大小
9) 从经验存储器中随机选取Ω批训练数据样本
10) 使用Adam 随机梯度下降算法更新神经网络参数θΩt
11) end if
12)t=t+1,进入下一状态st+1
13) end for
14) 输出(αI,αII,αIII),F*,P*
4 实验结果分析与讨论
基于海洋网络的计算任务卸载模型,本节在Python3.6 和Tensorflow 2.0.0 环境下对 OOPC-DRL算法进行了仿真实验。海洋网络仿真场景主要由强型层、中型层以及弱型层节点构成。网络环境下的计算任务卸载仿真参数如表2 所示。OOPC-DRL 算法中DNN 的相关设置参数参考文献[32],如表3 所示。

表2 网络环境下的计算任务卸载仿真参数
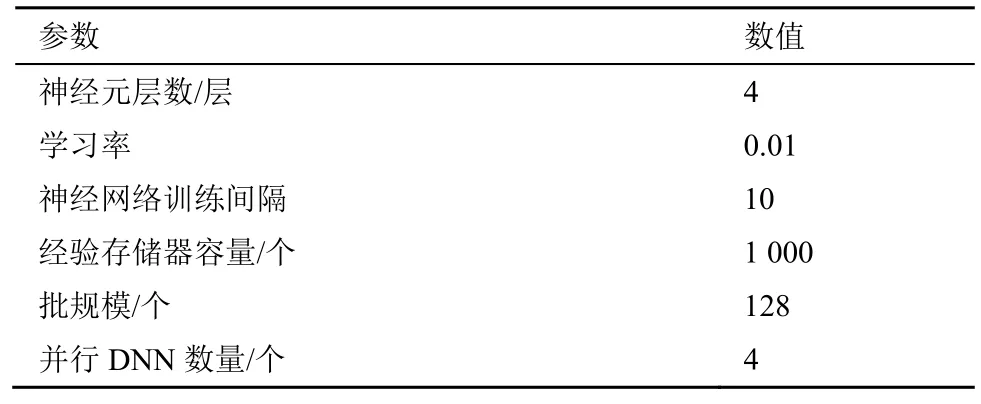
表3 DNN 的相关设置参数
为了分析OOPC-DRL 算法的收敛性能,本文将增益定义为其中,分子是通过枚举所有可行的卸载动作得到的最优解。

图3 和图4 分别展示了OOPC-DRL 算法的训练损失函数曲线和增益曲线。其中,训练损失随着训练步数的增加而降低,增益随着训练步数的增加而趋近于1。在训练初始时,DNN 需要不断探索动作,增益曲线会存在较大程度的波动。当训练步数在2 000 步时,训练损失和增益基本同时收敛;当训练步数大于2 000 步时,训练损失降低到0.04,增益收敛到0.98,这说明本文所提OOPC-DRL 算法可实现在有限训练步数内的稳定收敛,且能快速收敛到最优解。
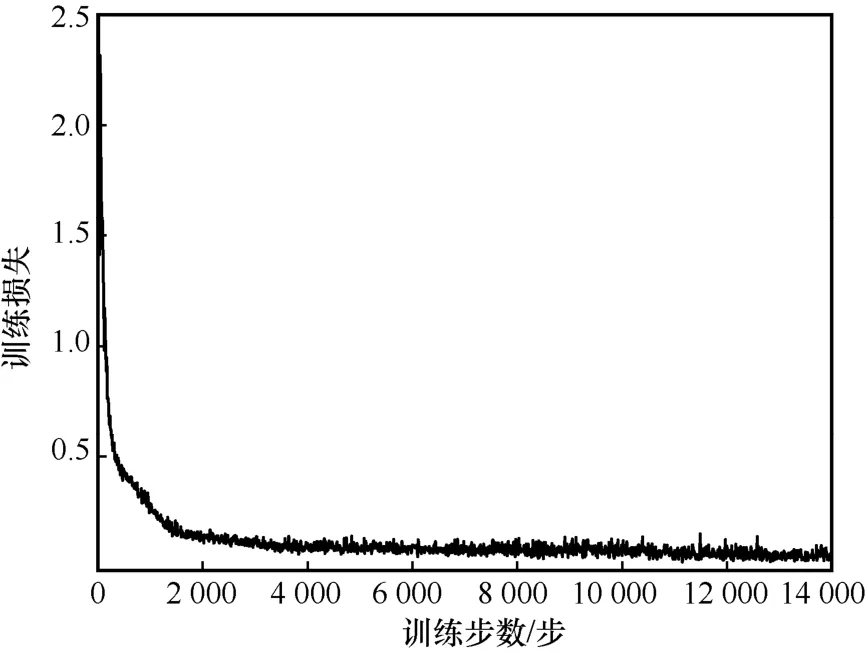
图3 基于OOPC-DRL 算法的损失函数曲线
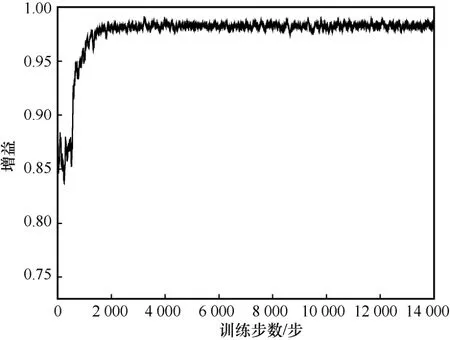
图4 基于OOPC-DRL 算法的增益曲线
图5 展示了DNN 数量对OOPC-DRL 算法收敛性能的影响。总体来看,随着训练步数的增加,增益逐渐收敛到1,且DNN 数量越多,收敛效果越明显。然而,当只使用一个DNN 时,OOPC-DRL 算法无法从其自身生成的数据中获取任何信息,并且无法收敛。因此,OOPC-DRL 算法至少需要2 个DNN。OOPC-DRL 算法的计算复杂度主要来自利用DNN 生成卸载决策矩阵阶段,当DNN 数量增加时,增益曲线虽然有所改善,但是效果并不明显,且算法的复杂度大幅度增加,因此,在设置DNN 数量时,需要权衡其性能和复杂度。所以,本文将DNN 数量设置为4。

图5 DNN 数量对OOPC-DRL 算法收敛性能的影响
图6 进一步说明了学习率对OOPC-DRL 算法收敛性能的影响。从图6 可以看出,随着训练步数增加,OOPC-DRL 算法在不同学习率下的增益均逐渐提升。学习率越大,OOPC-DRL 算法的增益曲线收敛越快。然而,当学习率为0.1 时,增益值反而降低,这是由于学习率过高导致网络陷入了局部最优的困局。相反,当学习率过低时(取值为0.000 1),算法收敛速度较慢,大约在训练4 000 步后达到收敛。因此结合这一实际情况,本文在剩余的仿真实验中将学习率设置为0.01。
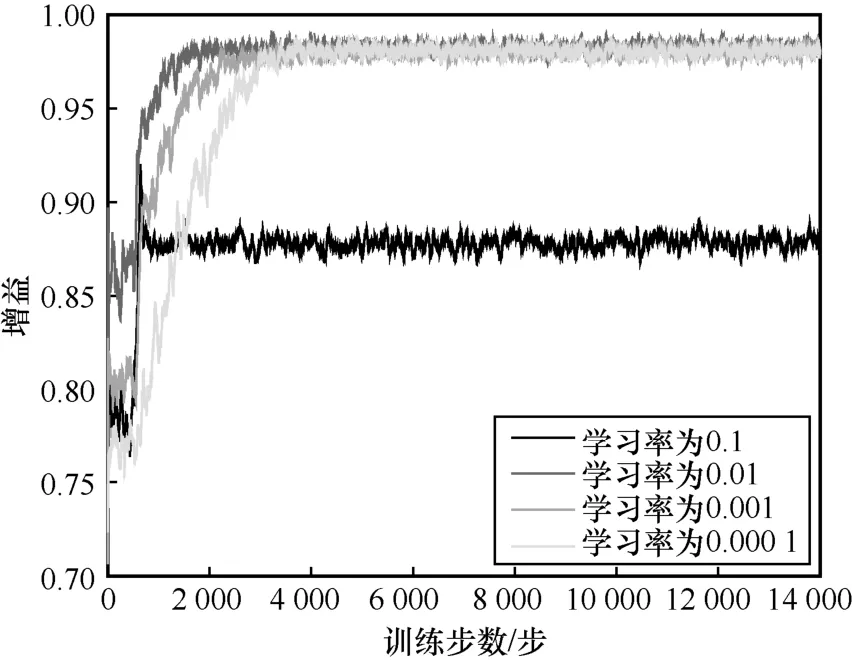
图6 学习率对OOPC-DRL 算法收敛性能的影响
为了验证OOPC-DRL 算法有效性,本文将其与以下5 种现有策略进行对比。
1) 本地计算策略(简称Local 策略)。节点的全部计算任务均在本地处理,不进行卸载处理。
2) 基于资源分配的随机卸载策略(简称Random策略)[33]。每当节点遇到新状态时,随机生成卸载动作,利用本文中的子问题优化方法分配计算资源。
3) 基于分组交叉学习的粒子群优化(GCL-PSO,group cross learning based particle swarm optimization)算法[25]。利用文献[25]中的GCL-PSO 算法生成卸载动作,通过本文的子问题优化方法分配计算资源。
4) 基于变异操作的人工鱼群算法(MO-AFSA,artificial fish swarm algorithm based on mutation operation)[26]。利用文献[26]中的MO-AFSA 生成卸载动作,通过本文的子问题优化方法分配计算资源。
5) 枚举(Enumerate)策略。对所有卸载决策进行穷举搜索,并选择最优卸载决策,但耗时过长,不能满足在实际情况中的实时性。
图7 展示了不同节点数量下各策略平均计算任务执行时延对比。从图7 中可知,除Local 策略外,其他策略的平均计算任务执行时延总体变化趋势均随着节点数量的增大而增加。这是因为当系统中节点数量增大时,单个节点分配的带宽和边缘服务器分配的计算资源相应减少,计算任务卸载传输时延和处理时延增加,导致平均计算任务执行时延增加。然而,本文所提出的OOPC-DRL 算法平均计算任务执行时延表现最优。Local 策略计算任务处理时延只与节点的性能有关,并且每个节点的计算能力远小于边缘服务器节点。因此,Local 策略在不同节点数量下的平均计算任务执行时延最高。Random 策略具有很强的随机性,在不同节点数量下的平均计算任务执行时延波动最大。由于寻优时容易陷入局部最优,MO-AFSA 和GCL-PSO 这2 种策略较OOPC-DRL 算法相比平均计算任务执行时延依次增加。通过以上对比可以看出,OOPC-DRL 算法平均计算任务执行时延接近具有最佳性能的Enumerate 策略,在降低节点平均计算任务执行时延方面具有较好的表现。
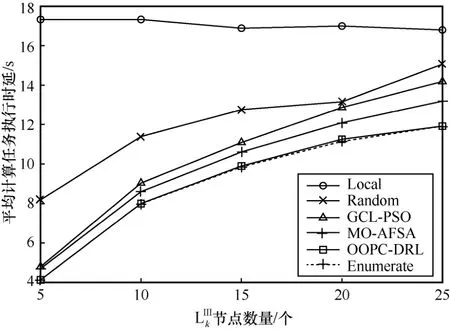
图7 不同节点数量下各策略平均计算任务执行时延对比
图8 展示了不同输入数据下各策略平均计算任务执行时延对比。从图8 中可以看出,随着输入数据的增大,除LOCAL 策略外,其他5 种策略的平均计算任务执行时延都有不同程度的增加,但是OOPC-DRL 算法相比其他策略表现更加优异,这是因为输入数据的大小只影响节点的任务传输时延。Random 策略由于存在随机性,其增加幅度最大,GCL-PSO 和MO-AFSA 策略容易陷入局部最优,寻优效果也不佳。OOPC-DRL 算法在不同输入数据下的平均计算任务执行时延接近Enumerate 策略,表现依然最好。在输入数据明显增大时,OOPC-DRL 算法相较其他策略提升更明显,再次说明该策略能够更好地应对资源有限情况下的任务分配问题,即能够在有限的资源情况下最小化系统时延。
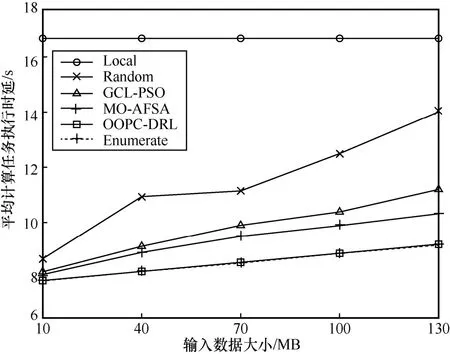
图8 不同输入数据下各策略平均计算任务执行时延对比
图9 展示了不同任务计算量下各策略平均计算任务执行时延对比。所有策略产生的平均计算任务执行时延均随着节点任务计算量的增大而增加,而Enumerate 策略和OOPC-DRL 算法的平均计算任务执行时延的增加幅度明显低于其他4 种策略。这是由于任务计算量增大时,节点需要花费更多的时间进行计算处理,而节点的计算能力最弱,故Local 策略的平均计算任务执行时延增加幅度最大。OOPC-DRL 算法的平均计算任务执行时延虽然随着节点任务计算量的增大而增加,但是始终非常接近能够产生最佳性能的Enumerate 策略,再次阐明了OOPC-DRL 算法在有限的资源情况下最小化系统时延的能力。

图9 不同任务计算量下各策略平均计算任务执行时延对比
图10 展示了不同计算能力下各策略平均计算任务执行时延对比(以固定输入数据大小为20 MB,任务计算量的大小为40 GHz 为例)。仿真结果表明,除Local 策略之外,其他策略的平均计算任务执行时延总体均随着边缘服务器计算能力的增大而降低,提高了节点任务执行效率。其中,OOPC-DRL算法在不同边缘服务器计算能力下的平均计算任务执行时延始终接近Enumerate 策略,均小于其他4 种策略,且随着边缘服务器计算能力越来越强,OOPC-DRL 与其他4 种策略的差距也越来越大。再次表明了本文所提算法随着边缘服务器计算能力的变化可以实时调整卸载策略,以确保系统具有更好的动态适应性。值得注意的是,Random 策略是随机生成卸载动作的,仿真时会出现50 GHz 下对应的平均计算任务执行时延高于40 GHz 的情况。
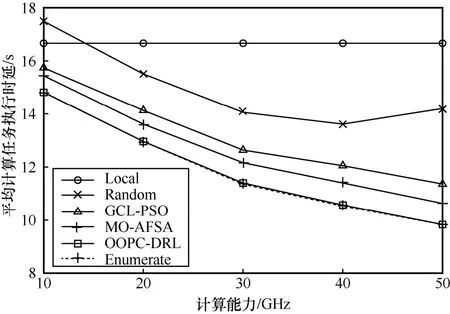
图10 不同计算能力下各策略平均计算任务执行时延对比
5 结束语
本文以最小化海洋网络节点任务执行时延为目标,利用海洋网络节点的强异构特征属性对其进行归类分层,并提出了一种基于深度强化学习的海洋网络计算任务卸载策略。实验结果表明,与传统算法相比,本文所提出的OOPC-DRL 计算任务卸载算法能够在海洋信息系统下有效地降低网络节点的计算任务卸载时延,可以更好地满足对实时性要求较高的海事应用服务需求,并且能够在大规模任务流下保持海洋网络的稳健性。未来研究工作将针对多维度的水上水下节点之间的任务卸载需求,深入分析并考虑排队等待时延对节点任务卸载的影响。

