高速移动环境下低复杂度OTSM 迭代rake 均衡方法
李国军,龙锟,叶昌荣,4,梁佳文
(1.重庆邮电大学超视距可信信息传输研究所,重庆 400065;2.重庆邮电大学光电工程学院,重庆 400065;3.重庆邮电大学通信与信息工程学院,重庆 400065;4.重庆邮电大学光电信息感测与传输技术重庆市重点实验室博士后科研工作站,重庆 400065)
0 引言
未来无线通信系统要求在高速铁路、无人机、自动驾驶等高移动性环境中进行可靠数据传输[1-3]。传统的正交频分复用(OFDM,orthogonal frequency division multiplexing)调制在面对频率选择性信道时,可以实现较高的频谱效率以及抗多径干扰[4]。然而在高速移动环境中,当前广泛采用的OFDM 会因载波间干扰(ICI,inter-carrier interference)导致其性能显著下降,如图1 所示。为改善高速移动环境下无线传输性能,Hadani 等[5-6]提出了正交时频空(OTFS,orthogonal time frequency and space)调制。OTFS 通过在时延-多普勒域复用信息符号,可以获得比OFDM 更完整的信道分集,从而产生优异的传输性能[7]。
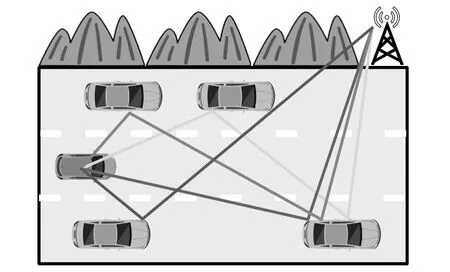
图1 高速移动平台多次反射传播
尽管OTFS 在高速移动环境下能产生优异的传输性能,但时频域中的二维预编码极大地增加了调制复杂度。最近,Thaj 等[8]提出了一种具有较低调制复杂度的正交时序复用(OTSM,orthogonal time sequency multiplexing)调制技术。如图2 所示,OTSM 通过在时延-序列域中复用传输信息符号,允许信道的时延扩展和多普勒扩展分别沿时延和序列维度引入符号间干扰(ISI,inter-symbol interference)并在接收机处分离,从而将时频域的快时变信道转换为时延-序列域上近似恒定的非衰落信道。
OTSM 可以看作二维码分多址(CDMA,code division multiple access)方案[5],与传统CDMA 系统不同,其信息符号在时间和频率上是分散的。在多径衰落信道的直接序列CDMA 中,rake 接收机可以通过合并调谐到各自时延偏移的匹配滤波器提取的传输符号的时延分量进行工作。类似地,OTSM 也可以提取接收信息符号的时延偏移和多普勒偏移并使用分集合并技术进行合并,以提高合并信号的信噪比。文献[9-11]分析了各种线性合并方案(如选择合并、等增益合并和最大比合并(MRC,maximum ratio combining))的rake 接收机。此外,迭代rake 合并接收技术已被证明能够更好地对抗符号间干扰[12]。
本文主要的研究工作如下。
1) 通过在OTSM系统时延-序列域放置能在时域充当交织保护带的零填充(ZP,zero padding),从而获得简化的信道输入输出关系。利用这种简化的信道输入输出关系,提出了一种低复杂度的MRC迭代rake 均衡器,简称为MRC 迭代均衡器。
2) 设计了单抽头时频均衡器来获得MRC 迭代均衡器的初始值[13],从而减少了MRC 算法的迭代次数且快速达到收敛。
3) 为进一步实现潜在的全信道分集并降低系统误码率,将turbo 技术应用于MRC 迭代均衡器,提出了基于OTSM 系统的MRC-turbo 接收机。
1 OTSM 系统模型
1.1 发送端与接收端
为方便起见,本文将以矩阵形式表示OTSM 系统传输模型。文献[8]给出了OTSM 系统传输模型,如图3 所示。OTSM 发送端首先将NM个信息符号x=[x1,…,xNM]放置于时延-序列域网格中,其中,空白格为空符号(即ZP),在避免块间干扰的同时允许插入导频进行信道估计[8],M为时延-序列网格的行数,N为时延-序列网格的列数且为2 的n次幂。时延-序列域矩阵X∈CM×N通过逐行进行沃尔什-哈达玛变换(WHT,Walsh-Hadmard transform)[14-15](与图2 沿序列域做IWHT 等价)转换为时延-时域矩阵
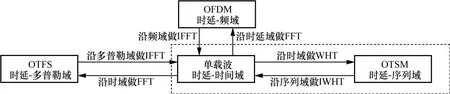
图2 不同离散信息符号域与相应调制方案之间的关系
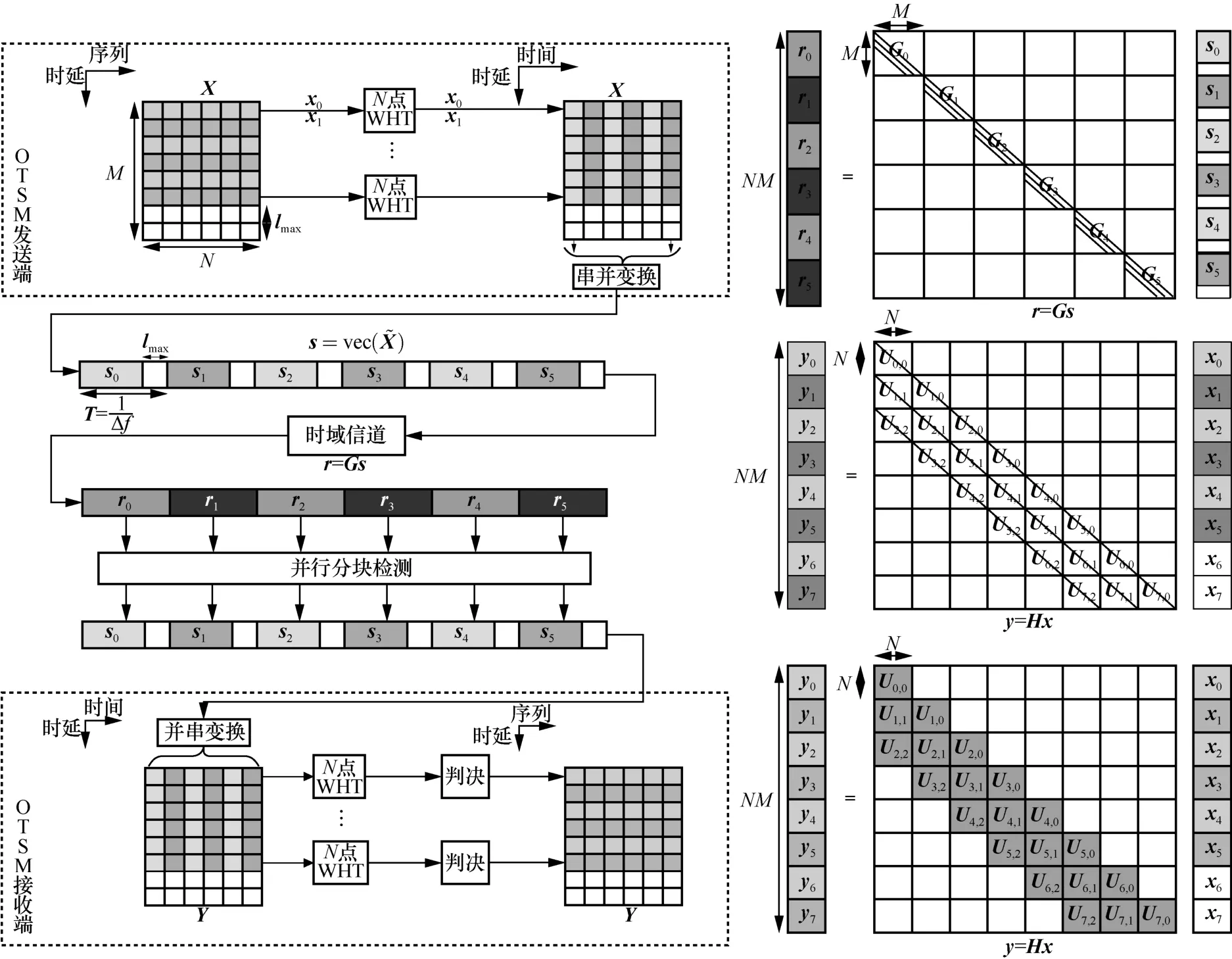
图3 OTSM 系统传输模型与不同离散信息域的输入输出关系

其中,WN为归一化N点WHT 矩阵。时延-时域矩阵经过矩阵逐列向量化后得到时域向量s∈CNM×1

如图4 所示,发送端操作可以用矩阵形式表示为

图4 时延-时域矩阵生成时域向量
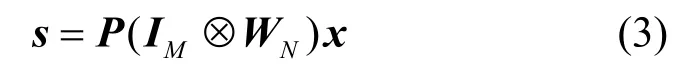
其中,P为行列交织器矩阵,IM为M行M列单位矩阵,⊗为克罗内克积。
在接收端,将时域向量r∈CNM×1按列填充至M×N矩阵,得到时延-时域矩阵

最后,经过WHT 得到接收到的时延-序列域矩阵Y∈CM×N

上述接收端操作可以用矩阵形式表示为

1.2 信道输入输出关系
由于时延-多普勒域信道中传播路径P的数目通常是有限的,因此信道响应可表示为[5,16]

其中,hi、τi和vi分别为第i条路径的路径增益、时延和多普勒频移。假设li和ki分别为第i条路径的归一化整数时延偏移和多普勒偏移,则第i条路径的实际时延和多普勒频移可表示为

其中,NT和MΔf分别表示OTSM 信号帧的帧持续时间和带宽。假设lmax为最大离散信道时延扩展索引,将时延-序列域矩阵X最后lmax行符号向量置零以避免由于信道时延扩展而引起的块间干扰。连续的时变信道冲激响应可表示为
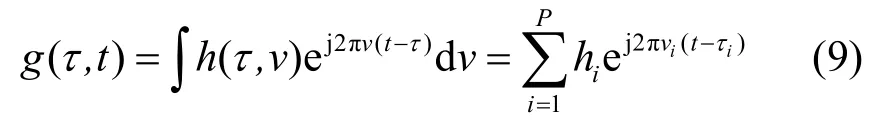
因此时域输入输出关系可以写为
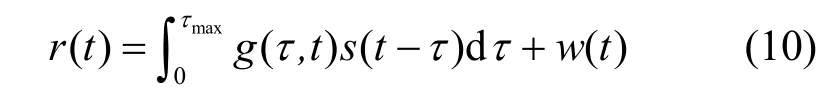

其中,G∈CNM×NM为时域离散基带信道矩阵,如图3 所示,在G的每行中有lmax+1个非零元素。
将式(3)和式(4)代入式(12),可得到时延-时域的输入输出关系为

2 低复杂度迭代rake 接收机
如图3 所示,ZP 防止了时域块之间的干扰,这使式(12)中的时域输入输出关系可独立处理
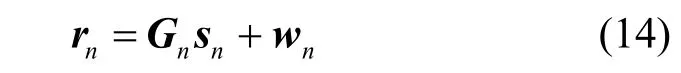
同样地,时延-时域等效输入输出关系可表示为
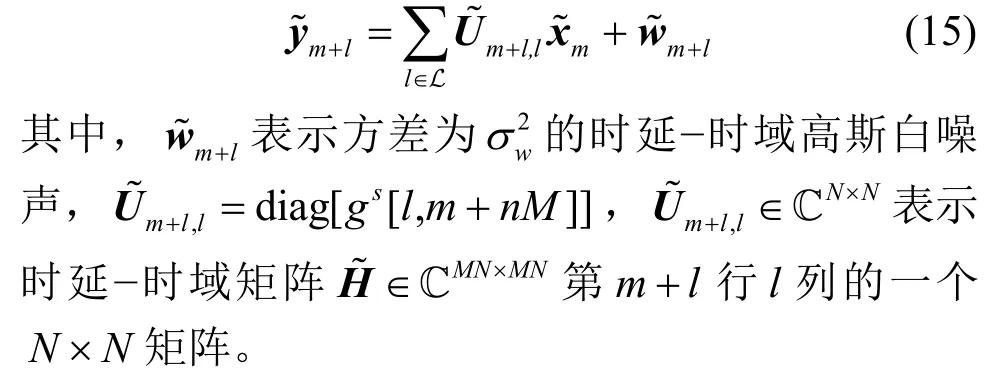
2.1 单抽头时频均衡器
在静态无线信道中,可以假设每个时域块的信道矩阵是循环矩阵并能在频域中进行对角化,但在高移动性信道中,多普勒扩展在每个块的频域信号之间引入干扰(时域信道矩阵由于时变信道而不再循环)。然而,由于每个时域块的持续时间比整个OTSM 帧的持续时间小很多,因此可以假设信道在每个块中是时不变的,但在每个块之间是不同的。这样可以在每个块中单独使用单抽头时频均衡器进行检测。

随后对每个块进行MMSE 均衡
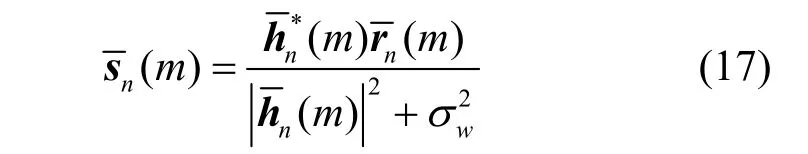
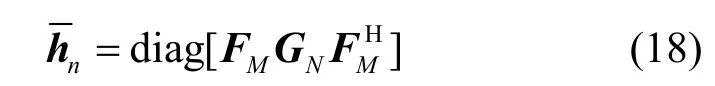
如图2 所示,时延-时域信息符号的估计值可通过时频域估计值进行M点IFFT 获得
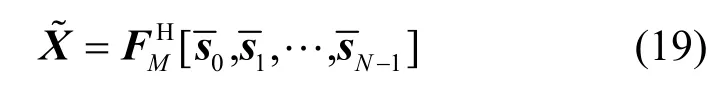
经过单抽头均衡器获得的时延-时域信息符号经判决后作为MRC 迭代均衡器的初始估计进行迭代检测,而获得的初始估计仅能为MRC 迭代均衡器提供更快的收敛速度。
2.2 基于MRC 的迭代rake 均衡器
本文所提出的MRC 迭代rake 均衡器可视为时延-时域网格中条不同时延分支处接收到的受损信号的最大比合并,如图5 所示。通过选择分支进行合并,从而提高合并后的信干噪比(SINR,signal to interference plus noise ratio)。
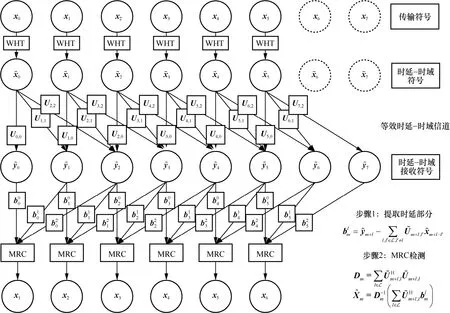
图5 基于MRC 的迭代rake 均衡算法步骤(M=8,L =0~2)
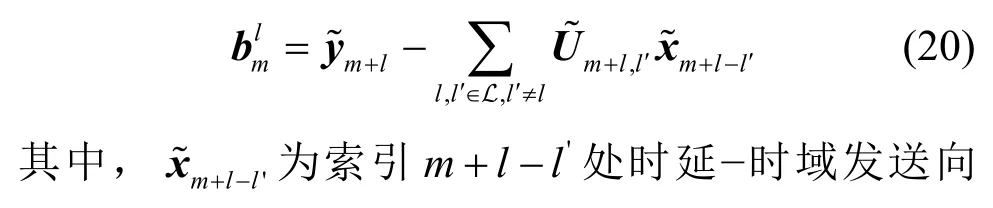

本文所提MRC 方案不是从式(20)中分别估计传输的符号,而是采用式(22)来估计的最大比合并,随后逐符号进行QAM解映射,得到判决出的第m个符号向量的n个符号
由图6可知,随着恒温搅拌时间的增加,磁性产品的产率逐步增大,赤铁矿的回收率逐渐升高。说明磁性颗粒随着搅拌时间的延长逐渐增加,当时间达到8 min时,弱磁性赤铁矿回收率基本上达到最高值。

设 D (·)表示每次迭代过程中对估计符号cm的判决,即。硬判决函数 D (c)由式(22)中的最大似然(ML,maximumlikelihood)准则给出,一旦更新了估计的时延-时域信息符号,本文将增加m并重复相同操作,随后以判决反馈的形式估计所有M'=M-lmax个时延-时域信息符号,算法1 给出了MRC 迭代均衡算法步骤。
算法1MRC 迭代均衡算法
1) fori=1:1:max iterations
2) form=0:1:M'-1
4) end for
5) 根据式(25)更新gm;
6) 根据式(23)更新cm;
7) 根据式(22)判决时延-时域信息符号;
8) end for
2.3 基于OTSM 系统的MRC-turbo 接收机
本节提出了一种基于OTSM 系统的MRC-turbo接收机,在发射端,信息比特经过随机交织、QAM调制以及OTSM 调制后传入信道;在接收端,首先使用单抽头时频均衡器获得初始QAM 符号的估计值,然后利用算法1 中提出的低复杂度MRC 迭代均衡器得到时延-时域估计值,最后进行turbo 迭代均衡。其中,每个turbo 迭代过程至少包含一个MRC迭代均衡器和一个LDPC 解码器,turbo 迭代次数可以根据所需的误码率和复杂性要求进行设置。
图6 给出了基于OTSM 系统的MRC-turbo 接收机工作原理,首先对MRC 迭代均衡器输出的估计信息符号进行OTSM 解调、QAM 软解调以获得每个比特信息的LLR,随后对其进行解交织并传递给LDPC 解码器。LDPC 解码器输出编码后的比特信息,然后对其进行交织、QAM 调制以及OTSM调制来获得改进后的时延-时域估计符号。
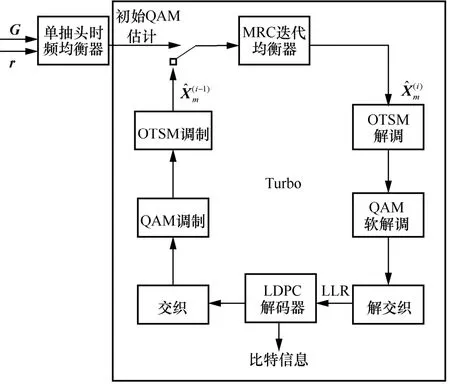
图6 基于OTSM 系统的MRC-turbo 接收机工作原理
3 计算复杂度分析
表1 总结了MRC 迭代均衡算法总计算复杂度。其中,①为每次MRC 迭代所需计算复杂度,算法1 中步骤3)和步骤5)的计算复杂度均为NM'L,步骤6)的计算复杂度为NM;②为计算初始值和Dm的计算复杂度,其中根据式(15)可得计算复杂度为NM'L,Dm根据式(24)可得计算复杂度为NM'P,P为接收机解析出的信道系数或传播路径的总数;③为计算单抽头均衡器的计算复杂度,其中式(16)、式(17)和式(19)的总计算复杂度为NM[L+2lb(M)+1]。

表1 MRC 迭代均衡算法总计算复杂度
为了保证仿真过程的公平性,本文所提出的MRC 迭代均衡器以及文献[13]提出的高斯-赛德(GS,Gauss-Seidel)迭代均衡器在开始迭代时均采用2.1 节所提出的单抽头时频均衡器作为其初始值。文献[17]给出了GS 迭代均衡器每次迭代所需的计算复杂度为O(NML2),而本文所提出的MRC迭代均衡器的计算复杂度仅为O(NML)。
4 仿真分析
本节研究了编码与未编码情况下的MRC 迭代均衡算法的误码性能,系统仿真参数设置如表2 所示。本节分别用误码率(BER,bit error rate)和误帧率(FER,frame error rate)表示未编码和编码情况下的解调性能,且对于BER 中的每个点发送 5 ×104OTSM 帧,FER 中的每个点发送104OTSM 帧,外部编码采用5G新空口(5G NR,5G new radio)方案中的标准LDPC码[18]。为避免信道估计误差带来的检测性能损失,本文假设信道响应在接收端是完全已知的,信道的多普勒频移由Jakes 公式生成,其中,vmax为最大移动速度,θi在[-π,π] 上均匀分布。此外,在BER 性能和实现复杂性方面比较了目前广泛使用的LMMSE 线性均衡器和GS 迭代均衡器。
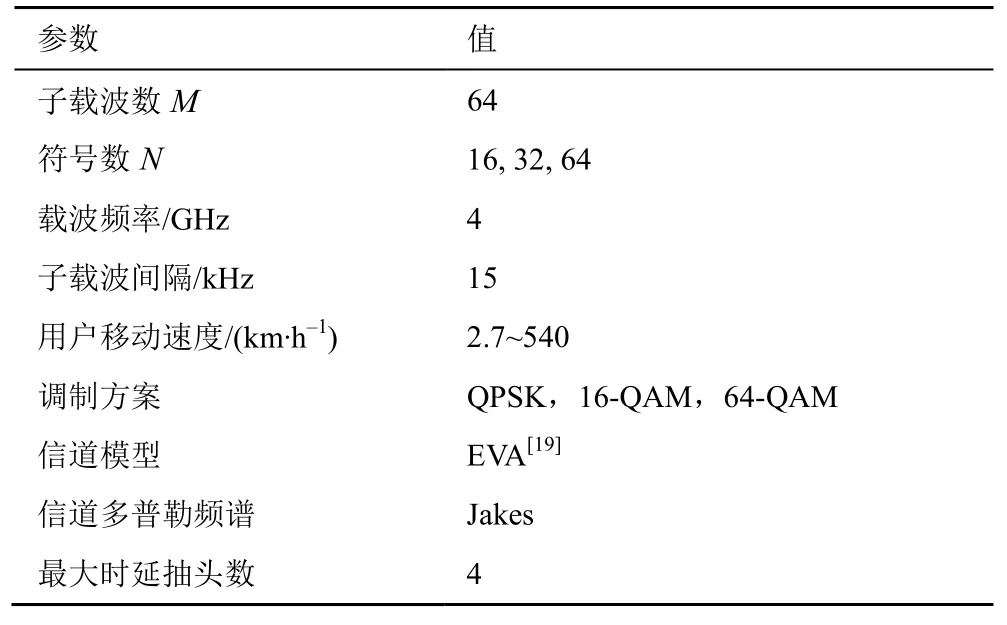
表2 系统仿真参数
图7 和图8 分别比较了在270 km/h 和540 km/h速度下不同算法的误码性能,其中,MRC 和GS 迭代均衡的QPSK、16-QAM、64-QAM 最大迭代次数分别设为5、15、35。仿真结果表明,MRC 迭代均衡器性能显著优于LMMSE 线性均衡器。如图7 所示,当BER=10-4时,对于QPSK 调制,MRC 迭代有2.34 dB 的性能增益。此外,与GS 迭代均衡器相比,MRC 迭代均衡器在QPSK、16-QAM 调制下的性能增益分别为0.62 dB 和0.8 dB。类似地,如图8 所示,当BER=10-4时,与GS 迭代均衡器相比,MRC 迭代均衡器在QPSK 和16-QAM 调制下的性能增益分别为0.63 dB 和1.02 dB。
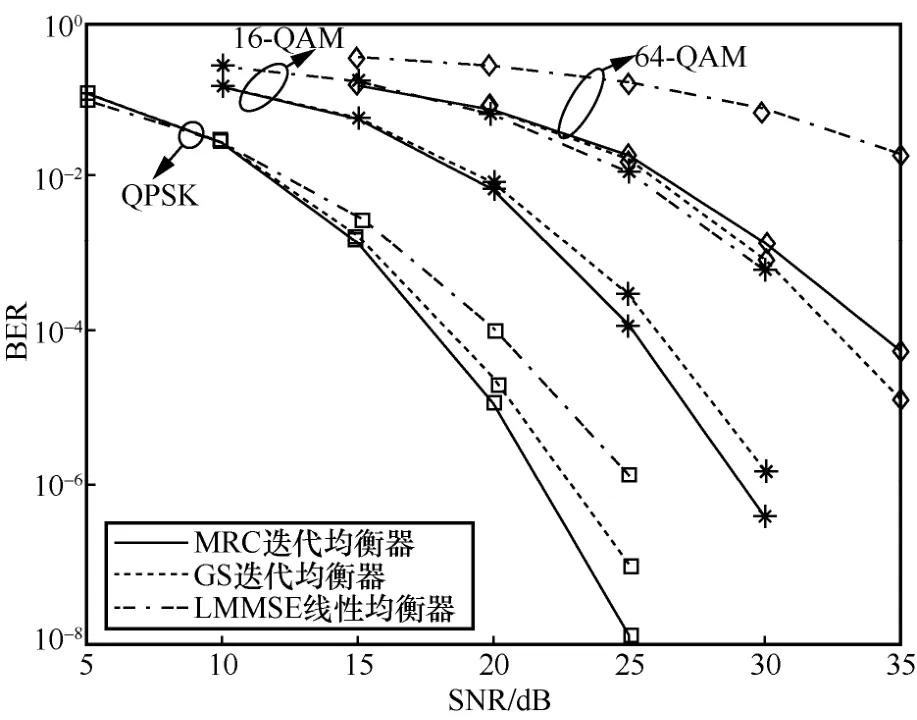
图7 在270 km/h(fd=1 000 Hz)速度下不同算法的误码性能

图8 在540 km/h(fd=2 000 Hz)速度下不同算法的误码性能
图9 给出了OTSM 系统在不同系统参数下的误码性能。从图9 中可以看出,随着N的增加,MRC迭代均衡器的性能也逐渐提升。这是由于增加OTSM 块大小可以提高多普勒频率的采样分辨率(即时延-序列域网格分辨率),接收机可以解析出更多的信道路径,从而提高误码率性能。

图9 OTSM 系统在不同系统参数下的误码性能
图10 给出了多普勒频移fd在10~2 000 Hz(对应的速度为2.7~540 km/h)时MRC 迭代均衡器的误码性能,这适用于大部分环境下的无线传输。从图10 中可以发现,随着fd的增大BER 反而越低,这一结果对于需要准静态信道的传统调制方案是令人意外的。实际上,在时延-序列域中调制可以受益于更大的多普勒频移,即较强的多普勒间干扰(IDI,inter doppler interference)不会恶化所设计均衡器的性能,而且还会改善其性能。这是因为接收机可以通过fd解析出更多的信道路径,从而提高误码率性能。
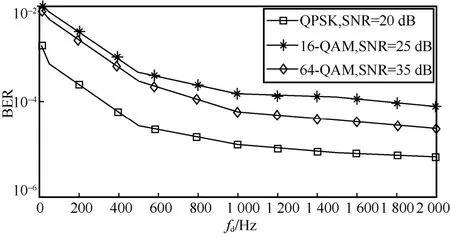
图10 fd 不同时MRC 迭代均衡器的误码性能
图11 给出了MRC-turbo 接收机在不同编码长度下的FER。从图11 中可以看出,对于不同的调制方式,编码长度越大,系统性能越好。
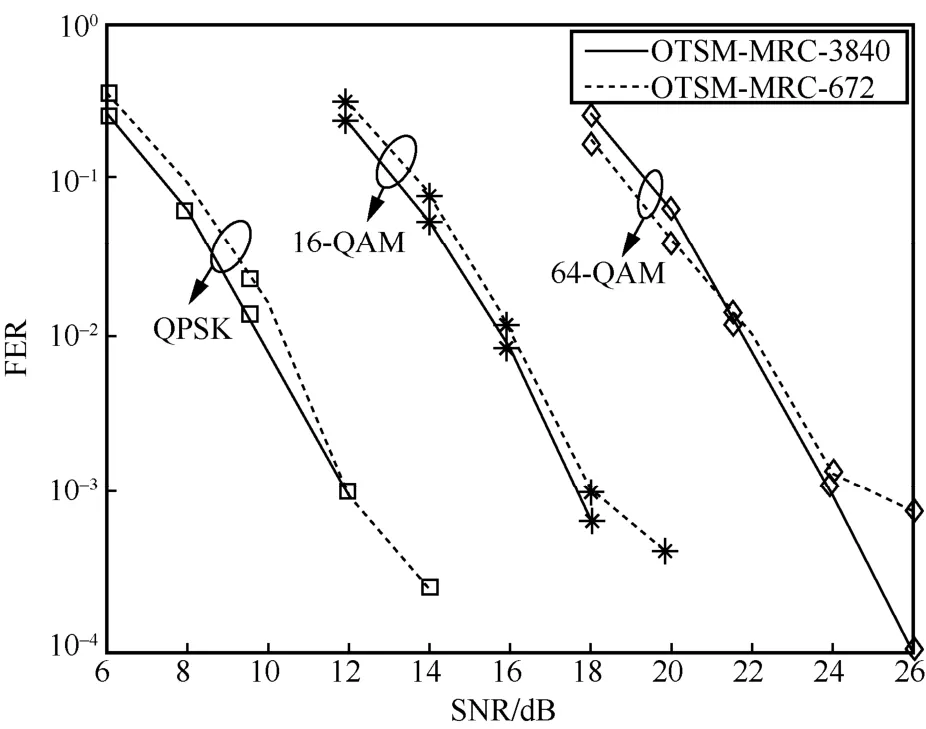
图11 MRC-turbo 接收机在不同编码长度下的误帧率
5 结束语
本文通过在时域中的每个块之间插入ZP,提出了一种用于OTSM 的低复杂度信道检测。首先,在接收端设计一个单抽头时频均衡器获得时延-时域信息符号预估值,随后作为MRC 迭代均衡算法的初始值在等效时延-时域网格中提取并相干地合并发射符号的接收多径分量来提高信号合并后的信噪比。为进一步提高系统性能,本文还提出了一种基于OTSM 的MRC-turbo 接收机。仿真结果表明,本文所提出的MRC 迭代rake均衡器能在高多普勒频移中取得良好性能。同时,与目前广泛使用的GS 迭代均衡器相比,MRC迭代均衡器在性能与计算复杂度上均有较大提升,这为未来高移动性通信系统提供了一种低复杂度均衡方案。

