考虑黄土结构性的浅埋隧道松动压力极限分析

靳正付，付大喜，杨明辉，胡珍宝

(1.河南省新融高速公路建设有限公司, 河南 洛阳 471027；2.北京交通大学 土木建筑工程学院，北京 100044； 2.河南省交通规划设计研究院股份有限公司， 河南 郑州 450015；4.湖南大学 土木工程学院，湖南 长沙 410082)

0 引言

黄土在我国华北及西北地区有着极为广泛的分布，而随着我国基础设施建设的蓬勃发展，黄土区出现了大量穿越于黄土层的浅埋隧道工程。此时，由于上覆土层较薄，围岩自稳能力较差，开挖过程中极易产生贯穿至地表的坍塌，由此给施工人员的生命安全带来了极大的不确定性。为合理分析浅埋隧道的稳定性问题，围岩松动压力是其中极为关键的重要指标，从而成为浅埋隧道设计计算的研究重点之一[1-2]。

不少学者已对浅埋隧道的围岩松动压力进行了深入研究。刘翔等[3]根据极限平衡法推导出了变坡面条件下浅埋偏压隧道松动围岩压力的计算公式。杨建民等[4]开展了大断面黄土隧道深浅埋分界、深浅埋围岩压力计算研究, 提出了大断面黄土隧道深浅埋分界高度及相应的围岩压力计算方法。于丽等[5]基于极限平衡理论推导了黄土区围岩压力及围岩滑裂面上围岩破裂角的计算公式。

极限分析法由于其概念清晰，已被越来越多的学者用于隧道围岩压力求解。如杨峰等[6]假定了浅埋隧道围岩的2种刚体平动破坏模式，通过上限法求得了浅埋隧道的围岩压力，证明了使用极限分析上限法计算隧道围岩压力的可行性。杨小礼等[7]则考虑到土体非线性破坏准则普遍适用性，以太沙基破坏模式为基础，使用极限分析上限法求解了浅埋隧道围岩压力的计算公式，并论证了非线性系数对围岩压力的重要影响。宋春霞等[8]采用极限分析法推导了非均质黏土地层中围岩压力的上限解，并讨论了土体的非均质性对围岩压力及破坏模式的影响。Leca等[9]构建了砂土隧道中掌子面的3种滑动破坏机构，通过极限分析法求得了保持掌子面稳定的极限支护压力。Wang等[10]利用正交试验法和UDEC确定了浅埋隧道在复杂地层的破坏模式，并在此基础上使用极限分析上限理论确定了松动区围岩压力计算公式。

值得注意的是，黄土在沉积过程中形成特有的大孔隙骨架结构，垂直节理发育明显，颗粒间胶结作用较强，这使得其具有显著结构性[11]。因此黄土区浅埋隧道的分析需考虑该问题，国内已有许多学者就结构性对实际工程的影响开展了大量研究。如邓国华等[12]基于黄土结构性和强度的关系，将结构性参数纳入芬那公式中，使其可更加全面地反映湿度变化和应力扰动对塑性区及支护力大小的影响。而在以往计算中大都忽略了黄土结构性对隧道围岩压力的影响。

因此，本研究以三轴试验为基础，分析试验过程中结构性参数的变化规律，进而将结构性参数引入摩尔库伦准则中。在此基础上，基于黄土特性构建浅埋黄土隧道的滑动破坏机构，使用极限分析上限定理推导出适于浅埋黄土隧道松动围岩的压力计算公式，并与现场实测数据与其他理论计算方法进行对比分析进行验证，从而为同类型隧道施工设计提供理论依据。

1 考虑黄土结构性的强度模拟

1.1 黄土结构性参数分析

由于受地理环境因素影响，黄土表现出独有的结构性特点，其抗剪强度势必受到影响。到目前为止，已有众多学者基于综合结构势思想提出了相应的结构性参数表达式，其中邓国华等提出的应力比结构性参数mη，可全面反映球应力和剪应力的影响，应用较为广泛：

(1)

式中(q/p)i，(q/p)r，(q/p)s分别为原状、重塑、饱和黄土剪应力与球应力的比值。

为分析黄土结构性与强度的关系，本研究首先提出了黄土在不同含水量和围压下的应力应变关系，以较全面地反映加荷、浸水和扰动对土体结构性的影响。试验用土为典型Q3黄土。围压分别选取50，100，200，300 kPa，同时选择5%，10%，15%，20%这4种含水量。图1为结构性参数随含水量、围压和应变的变化规律。

图1 各含水量结构性参数变化规律Fig.1 Variation rules of structural parameters with different water contents

从图1可知，土体的结构性参数mη随着含水量增加逐渐减小，但随着围压的增大而逐渐增大。同时，从整体来看，结构性参数随剪切变形的发展大致可分为2个阶段：第1阶段为结构性参数急剧下降阶段，该阶段通常发生在剪切变形的初期，此时土体结构的损伤会使结构性参数大幅、快速降低，这一阶段以原生结构的破坏为主导。第2阶段为结构性参数平稳发展阶段，随着剪切过程的持续发展，被破坏的土体结构在外界应力作用下会趋向于形成新的稳定结构，此时土体结构性参数下降幅度变得平缓，最终趋近于1。

1.2 强度参数与结构性参数的关系

为了定量表征结构性参数对土体强度的影响，诸多学者对其进行了大量的探索[13-14]，大多采用如下方法进行模拟：内摩擦角不随结构性参数的变化而变化，黏聚力与结构性参数之间符合近似的双曲线关系，即：

(2)

式中，a，b，F均为拟合参数。

然而，对于土体而言，随着应变的增加，其强度一般逐渐减弱，而式(2)中并没有体现结构性参数相对初始情况变化的相关参数，由文献[15]的推算结果，这可能会导致根据某一结构性参数值确定的黏聚力远大于土体正常黏聚力的情况。而土体的强度参数显然不能超过土体的初始强度参数。可见，分析结构性参数变化对土体强度的影响不能基于土体当前结构性参数绝对值大小，而应基于当前结构性参数相比于土体初始结构性参数变化值的大小。

为此，本研究引入结构性发挥度和强度参数发挥度的概念。即定义某初始状态下原状土的结构性参数为其对应的初始结构性参数。结构性发挥度Φη可定义为：

(3)

式中，mη为土体任一状态下的结构性参数；mη0为土体的初始结构性参数，可采用文献[16]中类似的方法确定，即对结构性参数与应变关系曲线中应变较小的部分进行线性延伸，取延伸线段与坐标轴纵轴的交点为零应变时土体的结构性参数。显然，土体结构性参数变化下限则为土体结构性完全丧失的状态，此时mη接近1。

相应的强度参数发挥度中黏聚力发挥度Φc和内摩擦角发挥度Φφ的定义如下：

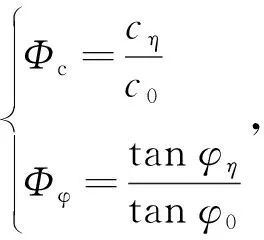
(4)

式中，cη为任一结构性参数mη对应的黏聚力；c0为土体结构强度完全发挥时的黏聚力；φη为任一结构性参数mη对应的内摩擦角；φ0为土体结构强度完全发挥时内摩擦角。

从而考虑结构性影响的摩尔-库伦准则可写为：

τ=cη+σtanφη=c0·Φc+σtanφ0·Φφ。

(5)

式中τ和σ分别为剪应力和正应力。

强度参数发挥度与结构性参数发挥度之间的关系见图2。可以看出，黏聚力发挥度与结构性参数发挥度之间符合线性关系，而内摩擦角发挥度基本不受结构性参数变化的影响。这说明，随着荷载的增加，土颗粒间开始产生相对滑移，土体的结构性开始逐渐发挥，在荷载增长的初期，主要是土体的摩擦特性在发挥作用，随着土颗粒间相对滑移的不断增大，即土体的结构性发挥到一定程度时，颗粒间的胶接结构也开始承担抵抗外力的作用，此时土体的黏聚分量也开始承担一部分外力，当土体的结构性接近完全发挥的临界状态时，土体的黏聚力达到最大值。

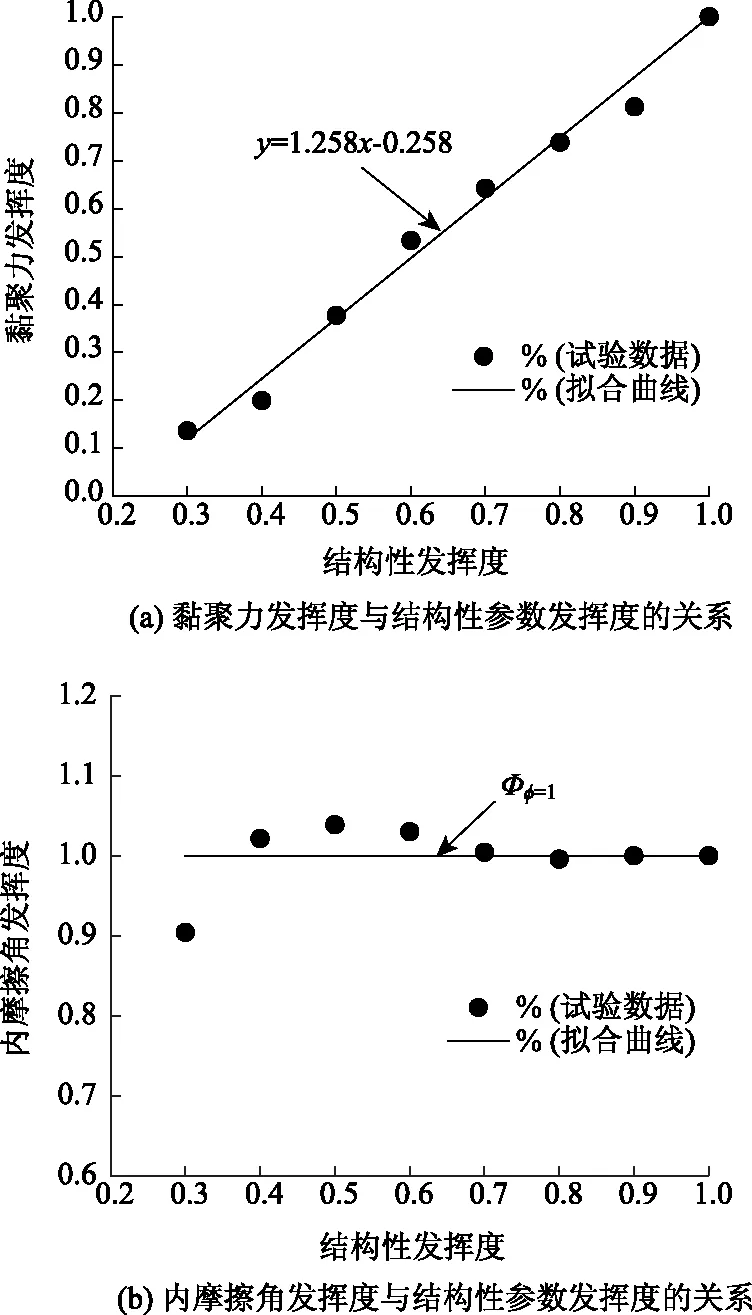
图2 强度参数发挥度与结构性参数发挥度的关系Fig.2 Relationships between strength parameter extent and structural parameter extent

通过对数据进行拟合可得到黏聚力发挥度与结构性发挥度之间的关系式：

Φc=a1Φη+b1,

(6)

式中a1和b1均为拟合参数。

2 黄土区浅埋隧道围岩松动压力求解

2.1 破坏模式构造

在确定土体强度参数后，即可构造黄土区浅埋隧道破坏模式。众所周知，黄土区存在明显的垂直节理，而从黄土隧道施工现场情况来看，隧道开挖过程极易形成坍塌至地表的直立滑动面，而非大多数学者采用的楔形滑动面[17]，因此本研究构建了浅埋黄土隧道破坏模式,如图4所示。其中, 隧道埋深为H；不失一般性将隧道简化为圆形截面，洞径为d，洞高为h；而隧道的破坏面包括从拱脚部分以破裂角α延伸至隧道顶板的BC和B1C1，以及从隧道顶板竖直贯穿至地表的AB和A1B1；隧道上覆土体ABB1A1的速度大小为v0，方向竖直向下；隧道两侧三角形楔体的速度大小为v1，其相对速度均为v01。隧道顶板处受均布支护反力为q，边墙处均布支护反力为e。根据相关联流动法则，所有速度与刚性滑块之间的速度间断线上的夹角均为φ，且各速度满足闭合条件，从而可得到图5所示的速度场。

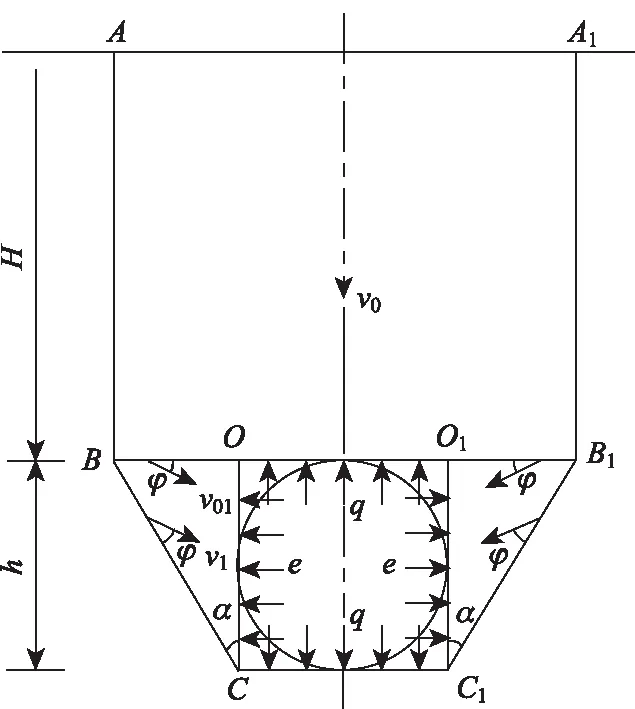
图3 浅埋隧道的破坏模式Fig.3 Failure mode of shallow tunnel

图4 破坏模式对应的速度场Fig.4 Velocity field corresponding to failure mode

图5 围岩压力现场监测试验Fig.5 Field monitoring test of rock pressure

2.2 上限解求解

极限分析上限定理已被广泛应用于岩土工程的各个领域，其定义可以表述为[18]：对于任意运动许可的位移场和塑性应变率场，根据虚功率方程式(7)所确定的荷载F一定不小于真实的破坏荷载F*：

(7)

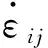
在使用极限分析上限定理研究浅埋黄土隧道的稳定性时，为方便计算作如下假设：(1)隧道围岩的破坏简化为平面应变问题进行分析；(2)假设某状态下整个隧道围岩的结构性发挥度为定值；(3)竖向松动压力q沿着拱顶均匀分布，侧向力e沿着边墙均匀分布。

2.2.1 外力功率和内能耗散率的计算

外力功率由土体重力功率WG和隧道支反力功率Ws组成，内能耗散率则为所有间断面上的能量耗散率之和。考虑到滑动机构的对称性，为简化计算，仅取滑动机构的左半部分分析。

(1)根据图4中的几何关系可求得间断线的长度AB,OB及滑动块体的面积S0,S1：

AB=H，OB=htanα,

(8)

(9)

(10)

2.2.2 外力所作功率

(1)土体重力功率

(11)

(12)

(13)

(2)竖向松动压力功率

-qhv0f3，

(14)

式中q为竖向松动土压力。

(3)速度矢量关系

由速度场满足相容条件可以得到各速度矢量之间的关系：

(15)

(16)

(4)内能耗散率

(17)

2.2.3 围岩松动压力的计算

根据虚功率原理，联立式(8)～式(17)可求得竖向松动土压力q的表达式：

(18)

式中f1～f4为关于α和φ的无量纲函数：

f1=0.5+tanα，

(19)

(20)

(21)

(22)

由式(18)可知，对于1组给定的参数，可确定相应的滑动机构和1个上限解q，因此式(18)的最优解的求解以转化成如下的数学模型：在给定的约束条件下，求解目标函数q=f(α,φ)的最大值，该最大值既是围岩压力的上限解，显然对于工程实际而言，其亦是保持隧道稳定所需支护力的最小值。

根据图4的速度场即可确定相应的约束条件：

π/2-α-2φ>0。

(23)

采用matlab软件中的序列二次规划算法，在指定约束条件内调整α和φ的值，直到得到最大的q值，该值即为优化上限解，而相应的破裂角α对应的就是最危险的滑动面。

3 结果验证分析

为验证本研究方法的准确性，在现场(河南省渑栾高速可乐湾隧道)3个不同掌子面进行了隧道上覆围压压力监测试验，其中隧道顶处土压力值可作为上覆松动压力值，如图5所示。将本研究方法计算结果与实测值及其他理论解进行了比较。具体参数如下：隧道宽度d=13.76 mm和高度h=9.692 m，围岩容重γ=18 kN/m3，内摩擦角φ=25°，黏聚力c=30 kPa，假设极限分析上限法中黏聚力和结构性参数发挥度之间满足式(6)的关系，结构性发挥度Φη取0.4。(该值由3个不同断面的围岩压力值反演得到，准确反演值为0.48，0.45，0.41)。对于太沙基法，侧压力系数K0取为1.0(极限分析法的K值根据太沙基法的e/q确定)。并将各方法得到浅埋隧道围岩压力计算结果，见表1(其中1-3断面为反演断面，而4-6个断面为验证断面)。

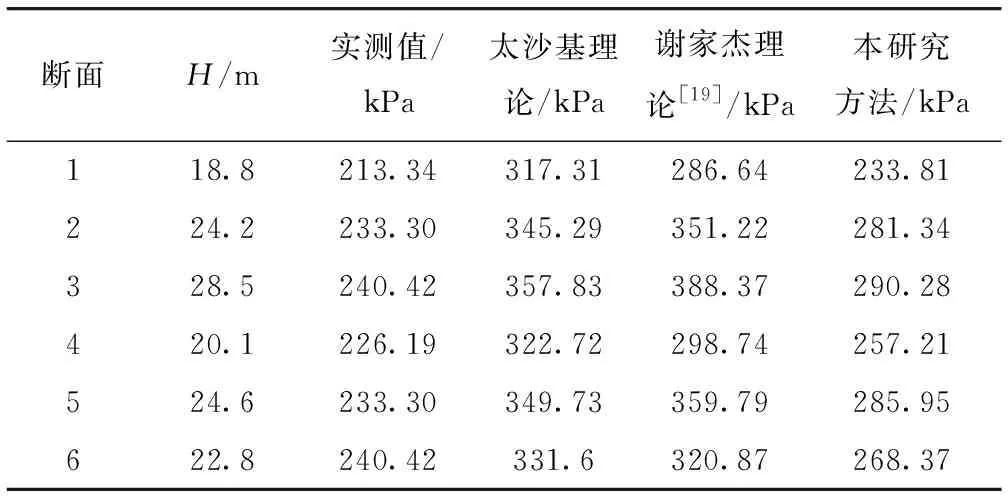
表1 实测值与理论值对比结果Tab.1 Comparison result between measured and theoretical values

由表1所示，所有理论的围岩压力计算结果都随着埋深的增加而增大，这和现场实测规律相吻合。但太沙基理论及谢家杰计算值较为保守。本研究的计算值与实测值更为接近，表明本研究方法在合理的结构性发挥度取值的情况下，围岩压力计算结果既可满足支护设计要求，还能在一定程度上节省工程造价。

4 影响因素分析

为进一步研究不同参数对浅埋黄土隧道松动压力的影响规律，基础参数取值参照上一节，各参数分析范围如下：隧道埋深H=10～30 m，隧道跨度和高度均取10 m，黄土重度γ=14～22 kN/m3，黏聚力c=30 kPa，结构性发挥度Φη=0.2～1.0，内摩擦角φ=20°～30°，侧压力系数K=0.5～1.0。将以上参数代入式(18)进行计算，即可得到不同参数变化对浅埋黄土隧道松动压力的影响规律，结果如图6所示。

图6 浅埋隧道上覆松动压力影响因素分析Fig.6 Analysis of influencing factors of loosening pressure on shallow tunnel

可以看出，当结构性发挥度一定时，随着侧压力系数K的增加，松动压力q呈非线性减小的趋势，如K值由0.5上升至1.0，松动压力q减小了近100%，且减小趋势先快后慢，这说明前期侧压力系数的变化对支护压力影响较大，后期影响趋于平缓。随着内摩擦角的增大，松动压力线性减小，因此在隧道施工过程中，对于土质较差的围岩，可考虑通过支锚注浆的方式改善围岩的物理力学性质，从而达到减小松动压力，提高隧道整体稳定性的效果。随着隧道埋深和围岩重度的增加，松动压力也同步线性增大，埋深和重度的增加相当于增加了隧道顶板上覆土体的滑动力，因而导致松动压力增大。此外，松动压力随着结构性发挥度的增大而减小，且结构性发挥度的改变对松动压力的影响较为明显，因此在浅埋黄土隧道施工过程中，应该谨慎选择开挖方式以及恰当的支护时机，避免对围岩结构造成急剧性的损坏，否则不利于黄土土体结构强度的发挥。

5 结论

本研究首先对黄土的结构性与强度的关系进行了分析，在此基础上，引入极限分析理论，对黄土区浅埋隧道的上覆围岩松动压力求解方法进行了探讨。主要结论如下：

(1)引入了黄土结构性发挥度的概念，提出了改进的强度参数和结构性参数关系的描述方法，使其可更完整地反映二者之间的关系。

(2)将考虑结构性影响的摩尔-库伦强度准则引入隧道的稳定性分析中，根据极限分析上限定理及工程实际构建浅埋黄土隧道的破坏模式，推导出黄土区浅埋隧道隧道围岩压力计算公式，并通过优化算法得到围岩压力的最优解。

(3)现场实测数据表明，黄土结构性发挥度大约在0.4～0.5之间。而黄土区浅埋隧道松动土压力与多因素相关。对比分析表明，松动围岩压力随着隧道埋深和围岩重度的增加而线性增长，但随着侧压力系数与土体强度的增加而减小。

(4)本研究提出了一种黄土结构性发挥度的模拟方法及其对围岩松动压力的影响，但由于其影响因素众多，且难以在实际工程中直接准确测定，因此该结构性与其他强度参数的准确关系仍有待于进一步深入研究。